How to Calculate the Volume of a Spherical Cap

Video Lesson: Calculating the Volume of a Spherical Cap

Volume and Surface Area of a Spherical Cap Calculator

The calculator below calculates the volume and surface area of a spherical cap.

Simply enter the following values:

  • ‘h’ is the height of the spherical cap
  • ‘r’ is the radius of the sphere
  • ‘a’ is the radius of the base of the spherical cap

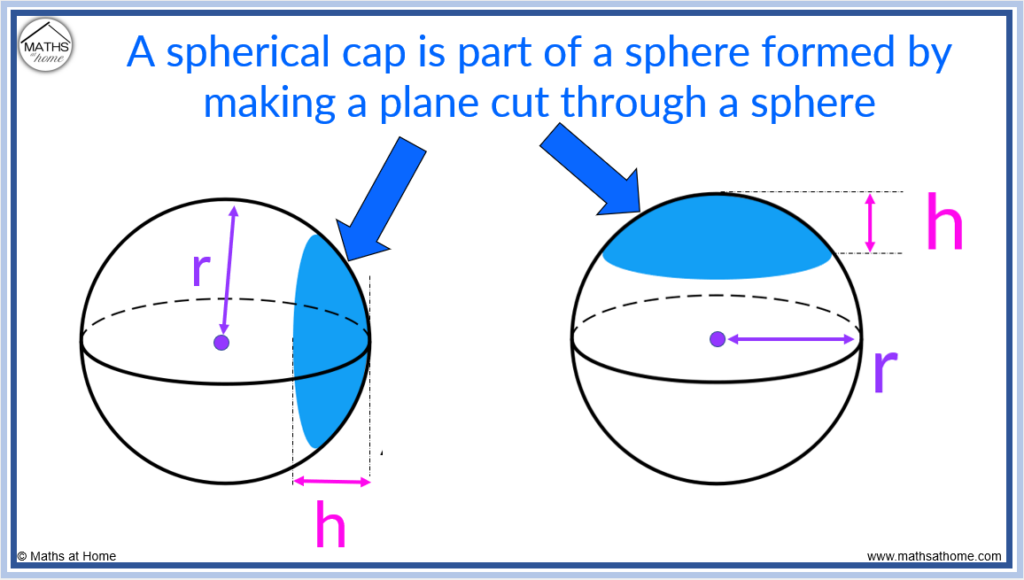
What is a Spherical Cap?

A spherical cap is a region formed by making any plane cut through a sphere. It has a curved spherical top face and a circular face on its base. The resulting shape looks like a cap which is on the top or side of a sphere.

Examples of spherical caps are shown in blue the image below.

Spherical caps are made whenever the side part of a sphere is cut off with a straight line.

definition of a spherical cap

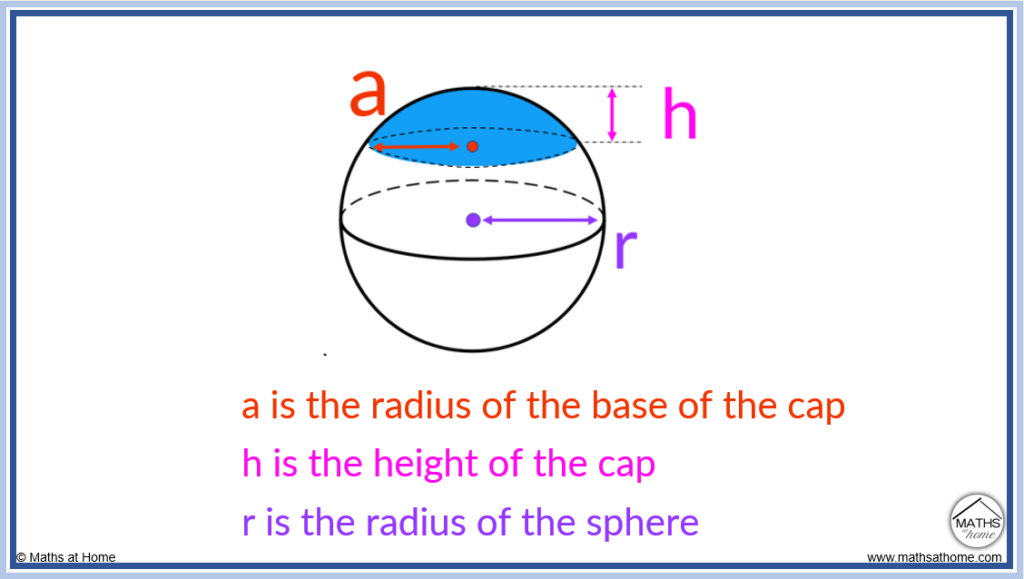
A spherical cap can be described using the values of ‘a’, ‘h’ and ‘r’.

  • ‘a’ is the radius of the circular base of the spherical cap
  • ‘h’ is the height of the cap
  • ‘r’ is the radius of the sphere
image of a spherical cap

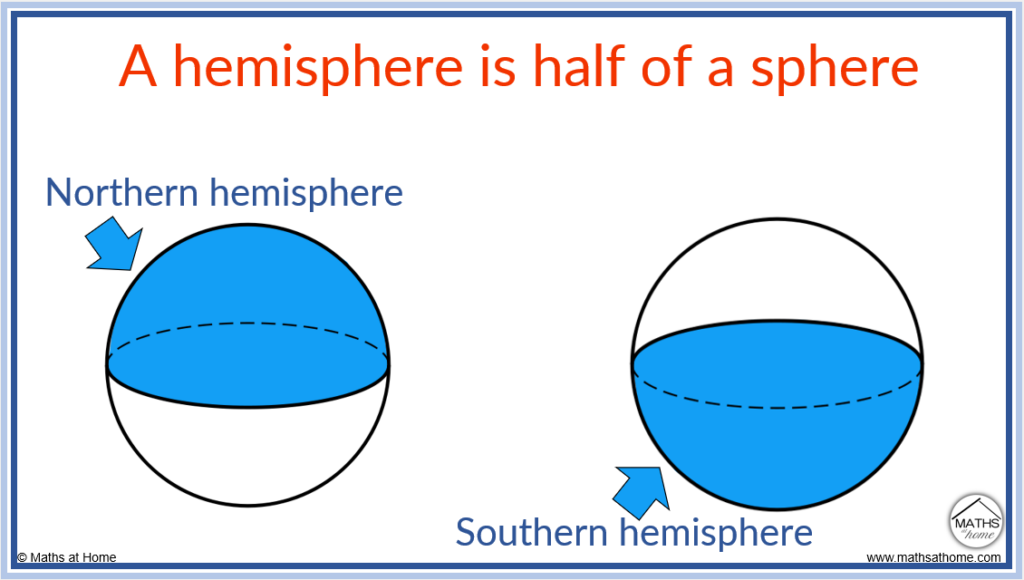
A hemisphere is an example of a circular cap in which the plane cut through the sphere passes exactly through the centre of the circle.

definition of a hemisphere

Formula to Find the Volume of a Spherical Cap

The volume of a spherical cap in terms of ‘r’ and ‘h’ is V = (πh2/3)(3r-h), where r is the radius of the sphere and h is the height of the spherical cap.

The volume of a spherical cap in terms of ‘a’ and ‘h’ is V =(πh/6)(3a2+h2), where a is the radius of the base of the cap and h is the height of the cap.

‘a’ is the radius of the circular base of the spherical cap
‘h’ is the height of the cap
‘r’ is the radius of the sphere

formula for the volume of a spherical cap
Formula for the Volume of a Spherical Cap when ‘h’ and ‘r’ are known
volume of a spherical cap formula
Formula for the Volume of a Spherical Cap when ‘a’ and ‘h’ are known

If the both the height of the cap, ‘h’ and the radius of the sphere, ‘r’ are known, then use the formula V equals pi h squared over 3 times open paren 3 r minus h close paren.

If both the radius of the base of the cap, ‘a’ and the height of the cap, ‘h’ are known, then use the formula V equals pi h over 6 times open paren 3 a. squared plus h squared close paren.

How to Find the Volume of a Spherical Cap

To find the volume of a spherical cap, substitute the values of the sphere radius ‘r’, and height of the spherical cap ‘h’, into the formula V = (πh2/3)(3r-h).

For example, calculate the volume of the spherical cap with a sphere diameter of 10m and a spherical cap height of 3m.

If the diameter of the sphere is 10m, then the radius is half of this.

The values of:

‘r’ = 5m

‘h’ = 3m

are substituted into V equals pi h squared over 3 times open paren 3 r minus h close paren.

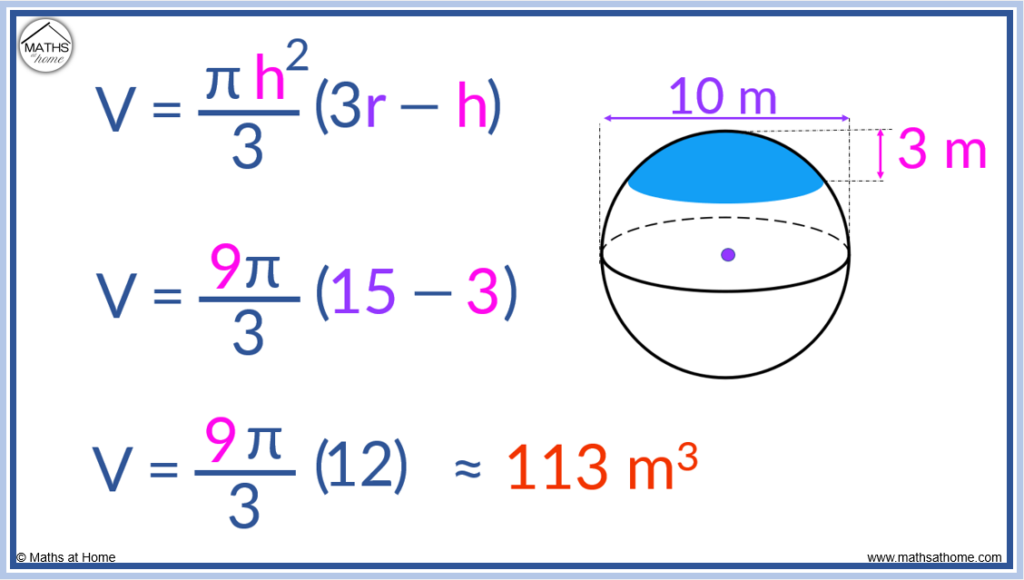
example of calculating the volume of a spherical cap

V equals pi h squared over 3 times open paren 3 r minus h close paren becomes V equals pi times 3 squared over 3 times open paren 3 times 5 minus 3 close paren.

Evaluating this further, we obtain V equals 9 pi over 3 times 12, which simplifies to V equals 36 pi.

The volume is approximately 113m3.

For example, calculate the volume of the spherical cap with sphere radius 3cm and spherical cap height of 2cm.

The values of:

  • ‘r’ = 3
  • ‘h’ = 2

are substituted into V equals pi h squared over 3 times open paren 3 r minus h close paren.

spherical cap volume example

V equals pi h squared over 3 times open paren 3 r minus h close paren becomes V equals pi times 2 squared over 3 times open paren 3 times 3 minus 2 close paren.

Evaluating this, we obtain V equals 4 pi over 3 times 7 which is approximately 29.3 cm3.

For example, calculate the volume of the spherical cap with base radius 5cm and a height of 2cm.

The values of:

  • ‘a’ = 5
  • ‘h’ = 2

are substituted into the formula V equals pi h over 6 times open paren 3 a. squared plus h squared close paren.

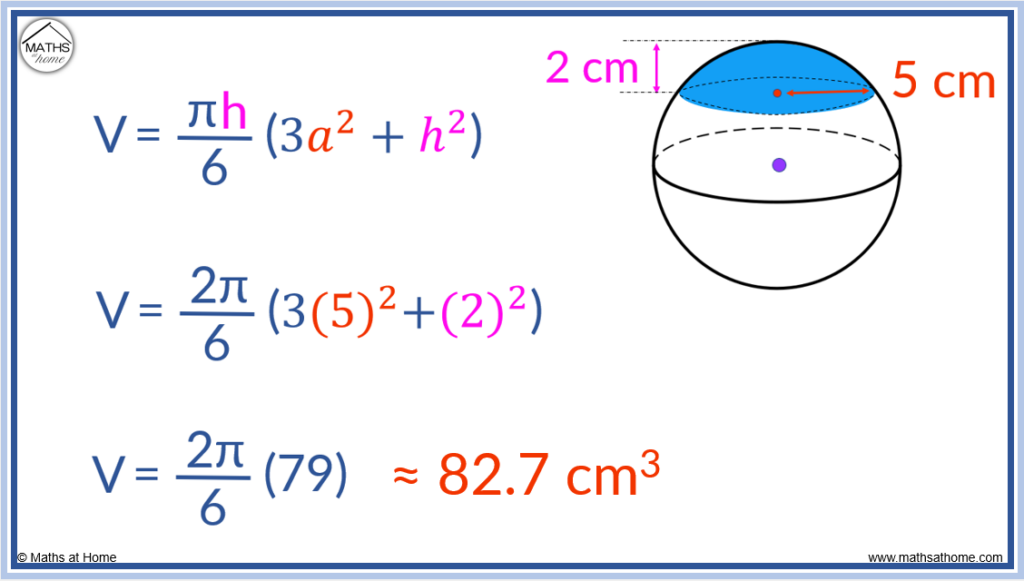
example of using the formula for volume of a spherical cap

V equals pi h over 6 times open paren 3 a. squared plus h squared close paren becomes V equals 2 pi over 6 times open paren 3 times 5 squared plus 2 squared close paren.

This simplifies to V equals 2 pi over 6 times 79 which is approximately 82.7 cm3.

Derivation of the Formula for the Volume of a Spherical Cap

The formula for the volume of a spherical cap can be derived by integrating π𝑥2 with respect to y between the limits of r and r-h.

The full derivation of the formula from integrals is shown below.

Step 1. Form the integral equation

The centre of the sphere is taken as the origin point, with the y-axis vertically and the x-axis horizontally.

The volume of the spherical cap can be found by finding the sum of the circular discs as shown in red below. Each circular disc has a different radius, which will be of length x.

The area of each circle is therefore πx2.

We want to sum the areas of the circles in the y direction. Therefore the volume is found as the integral of the integral from to of pi x squared d y.

In the y-direction, the top of the spherical cap is at a y value of r and the base of the cap is at a y value of r-h.

Therefore the volume is given by the integral V equals the integral from r minus h to r of pi x squared d y.

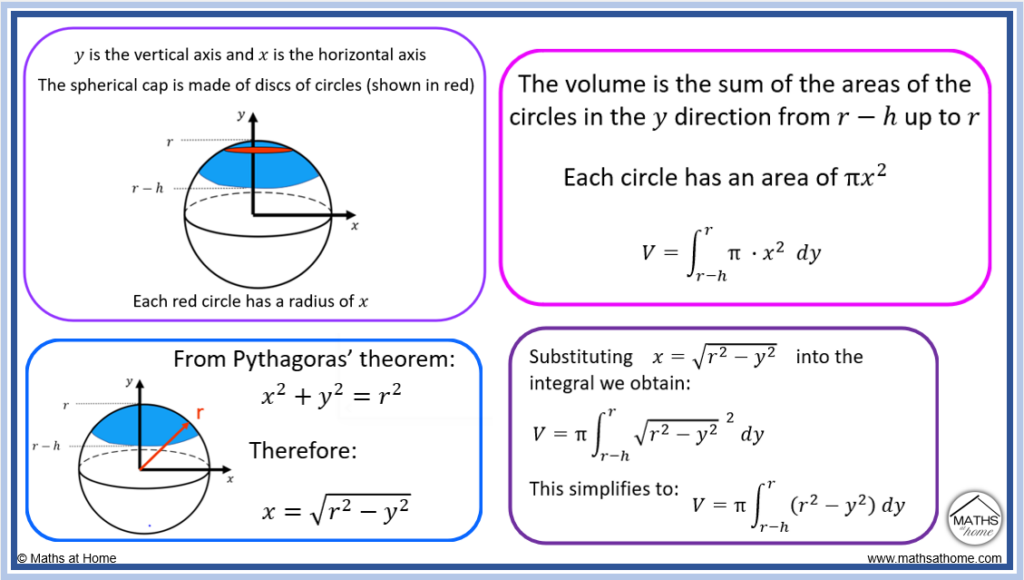
volume of a spherical cap integral

In order to be able to perform the integration, we need to find x in terms of y.

From Pythagoras’ theorem, the radius of the circle is connected to x and y by the equation x squared plus y squared equals r squared.

Rearranging for x, we obtain x equals the square root of r squared minus y squared.

Substituting x equals the square root of r squared minus y squared into V equals the integral from r minus h to r of pi x squared d y, we obtain V equals the integral from r minus h to r of pi times open paren the square root of r squared minus y squared close paren squared d y.

This simplifies to V equals the integral from r minus h to r of pi times open paren r squared minus y squared close paren d y.

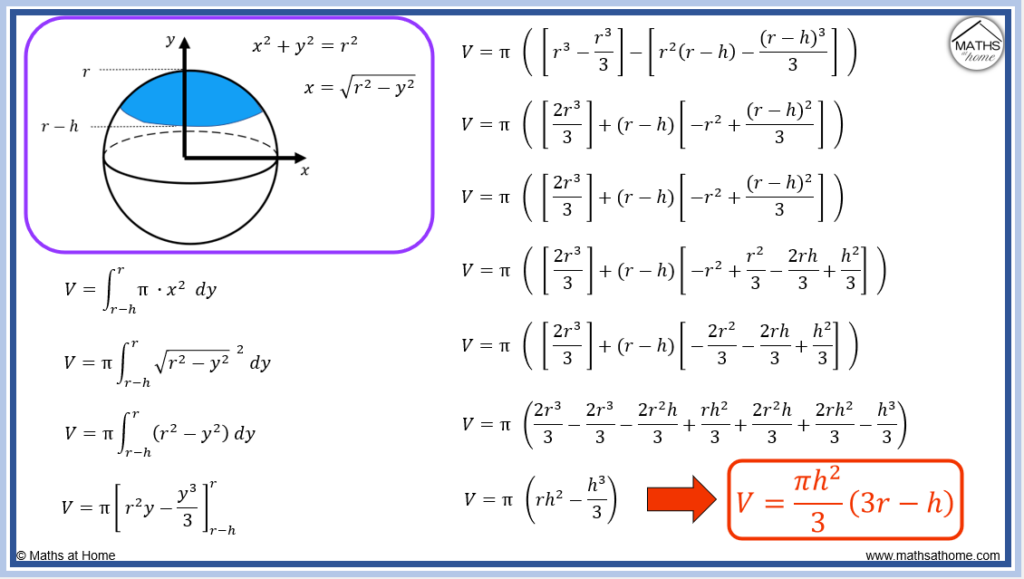
Step 2. Integrate and simplify

We now integrate V equals the integral from r minus h to r of pi times open paren r squared minus y squared close paren d y to obtain V equals pi times open bracket r squared y minus the fraction with numerator y cubed and denominator 3 close bracket sub r minus h to the power of r.

Substituting the limits of integration, we obtain V equals pi open paren open bracket r cubed minus the fraction with numerator r cubed and denominator 3 close bracket minus open bracket r squared times open paren r minus h close paren minus the fraction with numerator open paren r minus h close paren cubed and denominator 3 close bracket close paren.

This simplifies to V equals pi h squared over 3 times open paren 3 r minus h close paren following the algebraic steps shown below.

derivation of the volume of a spherical cap formula using integrals

Surface Area of a Spherical Cap

The curved surface area of a spherical cap is given by Area = 2πrh where r is the radius of the sphere and h is the height of the cap. Alternatively, the curved surface area is also given by Area = π(a2+h2), where a is the radius of the circle on the base of the cap and h is the height of the cap.

surface area of the curved face of a spherical cap
surface area formula for the curved face of a spherical cap

The base area of the spherical cap is πa2 and the total surface area of a spherical cap can be given by SA=2πrh+πa2 or SA=π(2a2+h2).

surface area of a spherical cap
surface area formula for a spherical cap

For example, calculate the total surface area of a spherical cap with a height of 4 cm and a cap base radius of 5 cm.

We substitute:

  • ‘a’ = 5
  • ‘h’= 4

Into the equation S A equals pi times open paren 2 a. squared plus h squared close paren to obtain S A equals pi times open paren 2 times 5 squared plus 4 squared close paren.

This can be evaluated to S A equals 66 pi which is approximately 207 cm2.

For example, calculate the outer surface area of a spherical cap with a height of 6 cm and a spherical radius of 12 cm.

We substitute:

  • ‘h’ = 6
  • ‘r’= 12

Into the equation S A equals 2 pi r h to obtain S A equals 2 pi of 12 times 6.

This can be evaluated as S A equals 144 pi which is approximately 452 cm2.