How to Calculate Variance

Video Lesson: How to Calculate Variance

What is Variance?

Variance is a measurement of the variability or spread in a set of data. It is calculated as the average of the squared deviations from the mean. The larger the variance, the more spread a set of data is. The variance is the square of the standard deviation.

The units of variance are the square of the units measured in the data set. For example, if the data measured is in seconds, then the variance is measured in seconds squared.

The variance does not have its own symbol and instead is written as the square of the standard deviation.

definition of variance
  • The sample variance is written using s2, where s is the sample standard deviation.

s squared equals the fraction with numerator Sigma open paren x sub i minus x horizontal bar close paren squared and denominator n minus 1

Sample variance formula
  • The population variance is written as σ2, where σ is the population standard deviation.

sigma squared equals the fraction with numerator Sigma open paren x sub i minus mu close paren squared and denominator N

Population variance formula

The mean is the average of the data, whereas the variance is a measure of how far each value in the data set is from the mean. The mean is a measure of centre and the variance is a measure of spread.

The variance depends on the value of the mean.

If the numbers in the data set are close to the mean, the data set will have a smaller variance.

If the numbers in the data set are far from the mean, the data set will have a higher variance.

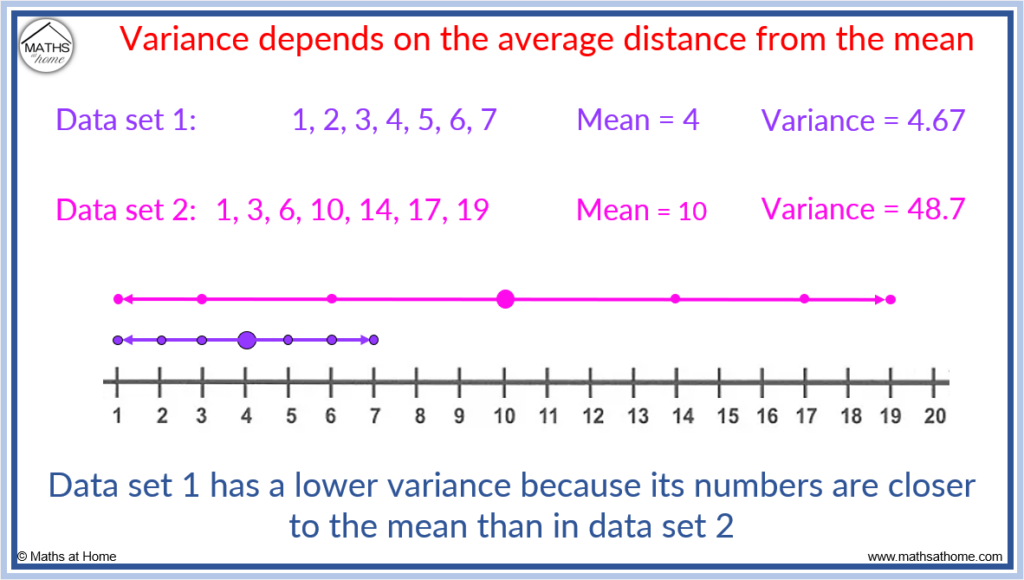
diagram explaining variance

The variance of a set of data cannot be negative. This is because the values are squared as part of the variance calculation. Squaring numbers always creates a positive result.

The variance of a set of data can be zero only if all of the numbers in the data set are equal. The variance is a measure of how spread out the numbers in the data set are. A variance of zero means that there is no spread in the data. The only way for this to occur is if all numbers are identical.

If the variance is not zero, it must be positive.

Small variance values indicate that there is little spread in the data. The closer the variance value is to zero, the less spread out the data is.

How to Calculate the Variance of a Data Set

To calculate the variance:

  1. Calculate the mean.
  2. Subtract the mean from each data value.
  3. Square these individual results.
  4. Add these results together.
  5. Divide this total by n-1 (for sample variance) or N (for population variance).

Example: Calculate the sample variance of the following data

3, 4, 6, 7, 7, 9, 13

how to calculate the variance of a data set

Step 1. Calculate the mean

The mean, x horizontal bar is given by the formula: x horizontal bar equals the fraction with numerator Sigma x sub i and denominator n.

To calculate the mean add the data values and divide by the number of data values.

Adding the data values: 3 + 4 + 6 + 7 + 7 + 9 + 13 = 49

There are 7 data values in the set so 49 ÷ 7 = 7.

The mean, x horizontal bar equals 7.

Step 2. Subtract the mean from each data value

A table is constructed with the data listed in the first column as xi.

The mean is subtracted from each individual value and written in the second column as xi-x̄.

xixi-x̄(xi-x̄)2
3-4
4-3
6-1
70
70
92
136

Step 3. Square these results

The values of xi-x̄ are squared to obtain (xi-x̄)2.

These values are written in the third column of the table.

xixi-x̄(xi-x̄)2
3-416
4-39
6-11
700
700
924
13636

Step 4. Add these results together

The sum of the values of (xi-x̄)2 are found as 16 + 9 + 1 + 0 + 0 + 4 + 36 = 66.

Step 5. Divide this result by n-1

For a sample variance, the sum of the (xi-x̄)2 values is divided by n-1, where n is the number of data values.

In this example, the sum of (xi-x̄)2 is 66 and n is 7.

Therefore n-1 = 6.

66 ÷ 6 = 11 and so, the sample variance of this data set is 11.

example of how to calculate the sample variance

Example: Calculate the population variance of the following data

1, 2, 5, 7, 10

how to calculate the population variance

Step 1. Calculate the mean.

The mean is found by summing the numbers in the data set and dividing by the number of numbers in the data set.

mu equals Sigma x sub i over N, where x sub i are the individual data values and N is the number of data values

The sum of the values is 1 + 2 + 5 + 7 + 10 = 25

There are 5 data values, so N = 5.

25 ÷ 5 = 5 and so, the population mean, mu equals 5

Step 2. Subtract the mean from each data value

The mean is 5. We subtract this from each of the data values.

We first create a table to organise the data with the data listed in the first column as xi.

We subtract the mean of 5 from each of these values to obtain the second column of the table, xi-µ.

xixi-µ(xi-µ)2
1-4
2-3
50
72
105

Step 3. Square these results

We square the values in the second column, xi-µ to obtain the values in the third column, (xi-µ)2.

xixi-µ(xi-µ)2
1-416
2-39
500
724
10525

Step 4. Add these results together

We find the sum of the (xi-µ)2 values by adding them.

16 + 9 + 0 + 4 + 25 = 54

Step 5. Divide this result by the number of data values

There are 5 data values in the data set.

N = 5.

Therefore we divide the sum of the (xi-µ)2 values by 5.

54 ÷ 5 = 10.8

Therefore the population variance of this data set is 10.8.

example of how to calculate population variance

The Difference Between Sample Variance and Population Variance

The population variance is calculated when the data considered is that of an entire population. The sample variance is used when the data considered is a sample of a larger set of data. The population variance formula has a denominator of ‘N’, whereas the sample variance formula has a denominator of ‘n-1’.

  • N is the size of the entire population of data
  • n is the size of the sample

N is always greater than or equal to n because n is a sample of N.

Population variance is calculated whenever data concerning the whole population is known. The mean used is the population mean, which is the known average of the entire population. The population mean is given by the symbol µ.

Sample variance is calculated when a sample of a larger set of data has been taken. The mean used is the sample mean, which is the mean of the data in the sample. The sample mean is given by the symbol x̄.

In the example shown below, the sample size is 4 and the population size is 64.

Therefore N = 64 and n = 4.

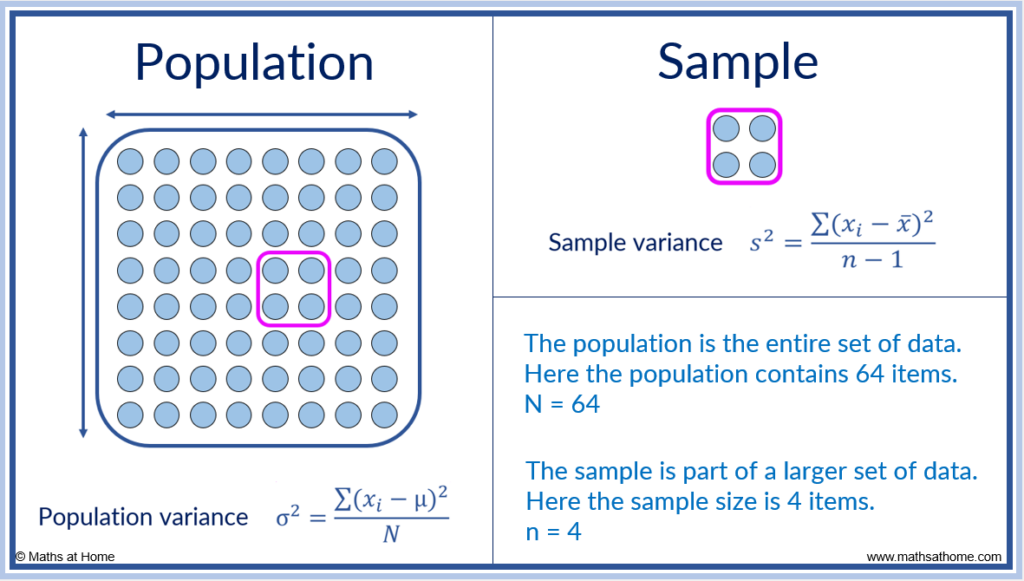
the difference between the population variance and the sample variance

The population variance has the formula sigma squared equals Sigma times open paren x sub i minus mu close paren squared over N.

The sample variance has the formula s squared equals the fraction with numerator Sigma times open paren x sub i minus x horizontal bar close paren squared and denominator n minus 1.

We can see that the denominator is different in both formulae.

In sample variance and standard deviation, a denominator of n-1 is used to reduce bias in the estimation of the population. Samples are taken to give an indication of the entire population data. Dividing by n-1 gives a sample variance or standard deviation that better reflects the population variance or standard deviation.

The denominator of ‘n-1’ is known as Bessel’s Correction Factor.

A division by ‘n-1’ is made in sample variance as it represents the number of degrees of freedom in the sample. The degrees of freedom is ‘n-1’ because the sample size is finite and the sample mean is known.

To explain this, consider a bookshelf full of books in which a sample of 4 books are considered. The total width of the 4 books is found to be 120mm and therefore the sample mean thickness of each book is 30mm.

If the width of the first book is measured to be 25mm, then the remaining 3 books must have a total width of 95mm. The width of the first book is the first degree of freedom.

If the width of the second book is measured to be 35mm, then the remaining 2 books must have a total width of 55mm. The width of the second book is the second degree of freedom.

If the width of the third book is measured to be 32mm, then the remaining book must have a total width of 23mm. The width of the third book is the third degree of freedom.

We do not need to measure the width of the fourth book as we already know it is 23mm wide. We found this by subtracting the other known values from the total width.

Therefore for a sample of 4 books, there were 3 degrees of freedom or three data values that are measured to calculate the sample variance.

The sample variance and standard deviation more accurately reflect the population variance and population standard deviation when the sample size is larger.

Variance from Standard Deviation

Both variance and standard deviation measure the spread of data. The variance is the square of the standard deviation. To find the variance from the standard deviation, square the standard deviation. To find the standard deviation from the variance, square root the variance.

The formula for population standard deviation is sigma equals the square root of Sigma times open paren x sub i minus mu close paren squared over N.

The formula for population variance is sigma squared equals Sigma times open paren x sub i minus mu close paren squared over N.

We see that we simply square the standard deviation to obtain the variance.

For example, if the standard deviation of a population is 2.3, then the variance of the population is 2.32 which is 5.29.

The variance is a measure of the average squared deviations from the mean.

In the standard deviation calculation, the square root cancels out the effect of the squaring that also takes place within the formula. Therefore the standard deviation can produce values that are easier to work with whilst still describing the spread of data.

Variance Formula

The sample variance is denoted with s2 and can be calculated using the formula: s2=∑(xi-x̄)2/[n-1]. In this formula xi represents each of the data values, x̄ is the sample mean and n is the number of data values.

the sample variance formula
s squared equals the fraction with numerator Sigma open paren x sub i minus x horizontal bar close paren squared and denominator n minus 1
Sample variance formula
  • s2 = the sample variance
  • xi = the individual data values
  • x̄ = the sample mean
  • n = the number of data values in the sample

The Σ symbol means to sum the values.

The formula can be explained in words as:

  • Subtract the mean from each data value
  • Square these answers
  • Add these answers up
  • Divide by one less than the number of data values

The population variance is denoted with σ2 and is calculated using the formula σ2=∑(xi–μ)2/[N]. In this formula, xi represents the individual data values, μ is the population mean and N is the number of data values.

the population variance formula

sigma squared equals Sigma times open paren x sub i minus mu close paren squared over N

The population variance formula
  • σ2 = the population variance
  • xi = the individual data values
  • µ = the population mean
  • N = the number of data values in the sample

The formula can be explained in words as:

  • Subtract the mean from each data value
  • Square these answers
  • Add these answers up
  • Divide by the number of data values

Variance of a Discrete Random Variable

To calculate the variance of a discrete random variable, use the formula σ2=Σ(xi-µ)2pi. To use this formula, subtract the mean from each data value, square each result, multiply each of these values by the corresponding probability and then add each of the results.

Two formulae can be used to calculate the variance of a discrete random variable:

sigma squared equals Sigma times open paren x sub i minus mu close paren squared p sub i

Formula 1 for variance of a discrete random variable

sigma squared equals Sigma x sub i squared p sub i minus mu squared

Formula 2 for variance of a discrete random variable
variance of a discrete random variable

For example, calculate the variance of the discrete random variable with the following probability distribution:

xi0123
pi0.250.150.50.1

Step 1. Calculate the mean

The mean, µ is found by multiplying each xi with its corresponding pi value and then adding the results together.

mu equals 0 times 0.25 plus 1 times 0.15 plus 2 times 0.5 plus 3 times 0.1

mu equals 1.45

Step 2. Use the variance formula

sigma squared equals Sigma times open paren x sub i minus mu close paren squared p sub i

This formula requires us to subtract the mean of 1.45 from each value, square each of these, multiply this by the corresponding probability and then add them up.

sigma squared equals open paren 0 minus 1.45 close paren squared times 0.25 plus open paren 1 minus 1.45 close paren squared times 0.15 plus open paren 2 minus 1.45 close paren squared times 0.5 plus open paren 3 minus 1.45 close paren squared times 0.1

sigma squared equals 0.9475

The variance is 0.9475.

Variance of a Continuous Random Variable

For a continuous random variable, the variance is calculated using the formula Var(X)=∫x2f(x)dx-µ2. The limits of integration are ‘a’ and ‘b’ where X is the continuous random variable with probability density function f(x) defined over the interval a≤x≤b.

V a. r of X equals the integral from a. to b of x squared f of x d x minus mu squared

Formula for the variance of a continuous random variable
  • f of x is the probability density function
  • The mean or mu equals the integral from a. to b of x f of x d x

For example, find the variance of the continuous random variable X defined by the probability density function f of x equals one half x over the interval 0 is less than or equal to x is less than or equal to 2.

Firstly, the mean is calculated using mu equals the integral from a. to b of x f of x d x.

mu equals the integral from 0 to 2 of x of one half x d x which simplifies to mu equals the integral from 0 to 2 of one half x squared d x.

Performing the integration, mu equals open bracket the fraction with numerator x cubed and denominator 6 close bracket sub 0 squared and evaluating this, we obtain mu equals four thirds.

Now we substitute this into the variance equation so that V a. r of X equals the integral from a. to b of x squared f of x d x minus mu squared becomes V a. r of X equals the integral from 0 to 2 of x squared of one half x d x minus four thirds squared.

Simplifying, we obtain V a. r of X equals the integral from 0 to 2 of one half x cubed d x minus sixteen ninths.

Performing the integral, we obtain V a. r of X equals open bracket the fraction with numerator x to the fourth power and denominator 8 close bracket sub 0 squared minus sixteen ninths.

Evaluating this, V a. r of X equals 2 minus sixteen ninths and V a. r of X equals two ninths.

Variance of a Binomial Distribution

The variance of a binomial distribution is calculated by σ2=np(1-p) where n is the number of trials and p is the probability of success.

sigma squared equals n p times open paren 1 minus p close paren

Variance formula for a binomial distribution

For example, a fair dice is rolled 12 times. Let X be the number of fives rolled. Calculate the variance of X.

  • n = 12
  • p = 1/6
  • (1-p) = 5/6

Therefore sigma squared equals 12 times one sixth times five sixths

sigma squared equals ten sixths

sigma squared almost equals 1.67

Variance of a Bernoulli Random Variable

The variance of a Bernoulli random variable is given by σ2=p(1-p) where p is the probability of success.

sigma squared almost equals p times open paren 1 minus p close paren

Variance formula for a Bernoulli random variable

For example, a spinner containing 6 red and 4 blue sections is spun. Let X = 1 is the spinner lands on a red and X = 0 if the spinner lands on a blue. Calculate the variance of X.

p is the probability of success. A success here is obtaining a red since this is where X = 1.

Therefore p = 6/10

sigma squared almost equals p times open paren 1 minus p close paren

sigma squared equals six tenths times four tenths

sigma squared equals 24 over 100

sigma squared equals 0.24

How to Calculate Variance in Excel

To calculate sample variance on excel, use the function =VAR.S(). Type =VAR.S() in the cell you wish to use and in between the brackets type the cells containing the data.

For example, find the sample variance of 1, 4, 4, 6, 9, 12 as shown below.

We enter the data 1, 4, 4, 6, 9, 12 in the cells from A1 to A6.

In a different cell we type=VAR.S() and in between the brackets we type A1:A6 which means that it will consider all of the data values from A1 to A6.

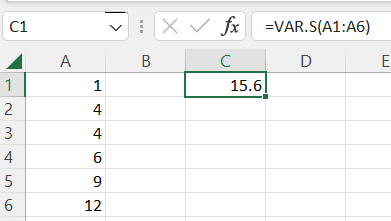
how to calculate sample variance on excel

We obtain a sample variance of 15.6.

To calculate sample variance on excel, use the function =VAR.P(). Type =VAR.S() in the cell you wish to use and in between the brackets type the cells containing the data.

For example, find the population variance of 1, 4, 4, 6, 9, 12 as shown below.

We enter the data 1, 4, 4, 6, 9, 12 in the cells from A1 to A6.

In a different cell we type=VAR.P() and in between the brackets we type A1:A6 which means that it will consider all of the data values from A1 to A6.

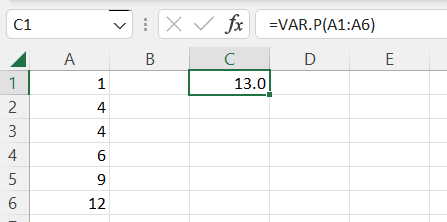
how to find population variance on excel

We obtain a population variance of 13.0.

How to Calculate Variance on a Ti-84

To calculate the variance on a Ti-84:

  1. Press STAT and select 1: Edit from the list.
  2. Enter the data in List 1.
  3. Press STAT and select 1: 1-Var Stats from the CALC menu.
  4. Ensure the List is set to L1 and select calculate.
  5. Square the values of sx (sample) or σx (population).

Calculate the variance of the following data using a Ti-85 Texas Instruments Calculator

Data set: 1, 4, 4, 6, 9, 12

The population variance is 13.0.

The sample variance is 15.6.

Step 1. Press STAT and select 1: Edit from the list

the stat menu on the ti-84

Step 2. Enter the data in List 1

The data is entered in the first column L1.

entering a list of data on the ti-84 calculator

Step 3. Press STAT and select 1: 1-Var Stats from the CALC menu

We press STAT and use the right arrow to scroll across to the CALC list.

Press 1 to select the 1-Var Stats option.

the stat calc menu on ti-84 calculator

Step 4. Ensure the List is set to L1 and select calculate

On the screen below, ensure that List is set to L1 and FreqList is left blank.

Scroll down to calculate and press enter.

calculating 1 var stats on ti84

Step 5. Square the values of sx (sample) or σx (population)

In the list below, Sx is the sample standard deviation and σx is the population standard deviation.

Square these values to obtain the sample variance and population variance respectively.

3.605552 = 13.0 and so, the population variance is 13.0.

3.949682 = 15.6 and so, the sample variance is 15.6.

1-var stats list on a ti-84 calculator

How to Calculate Variance on a Casio fx-CG50 Calculator

To calculate variance on a Casio fx-CG50:

  1. Click on menu and select statistics.
  2. Enter the data in List 1.
  3. Press F2 to select the CALC option.
  4. Press F1 to select the 1-VAR option.
  5. Square the values of sx (sample) or σx (population).

Calculate the variance of the following data using a Casio fx-CG50

Data set: 1, 4, 4, 6, 9, 12

The population variance is 13.0.

The sample variance is 15.6.

Step 1. Click on menu and select statistics

The statistics option is shown below.

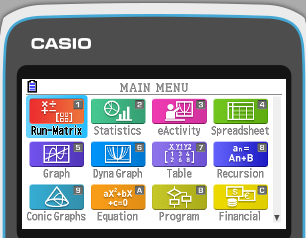
casio fxcg50 menu screen

Step 2. Enter the data in List 1

The data list of 1, 4, 4, 6, 9, 12 is entered vertically in List 1 as shown below.

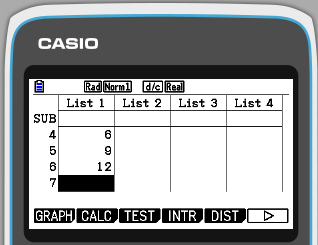
entering a list in casio fxcg50

Step 3. Press F2 to select the CALC option

The F2 button at the top is directly below the CALC option as shown on the screen above.

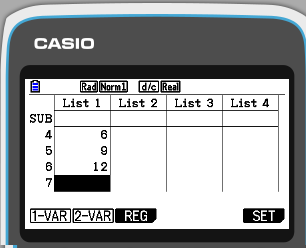
using the calc options on casio fxcg50
Step 3. Press F1 to select the 1-VAR option

The F1 button is directly below the 1-VAR option as shown on the screen above.

Step 4. Square the values of sx or σx

sx is the sample standard deviation and σx is the population standard deviation.

Both values appear in the list below.

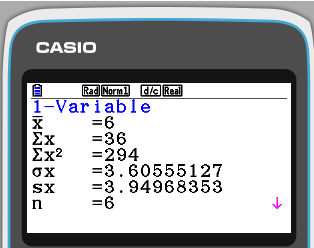
the 1-var stats list on a casio fxcg50

To obtain the variance from the standard deviation, square the standard deviation.

3.605552 = 13.0 and so, the population variance is 13.0.

3.949682 = 15.6 and so, the sample variance is 15.6.