Video Lesson: How to Find a Vector Perpendicular to a Plane
How to Find a Vector Perpendicular to a Plane from 3 Given Points
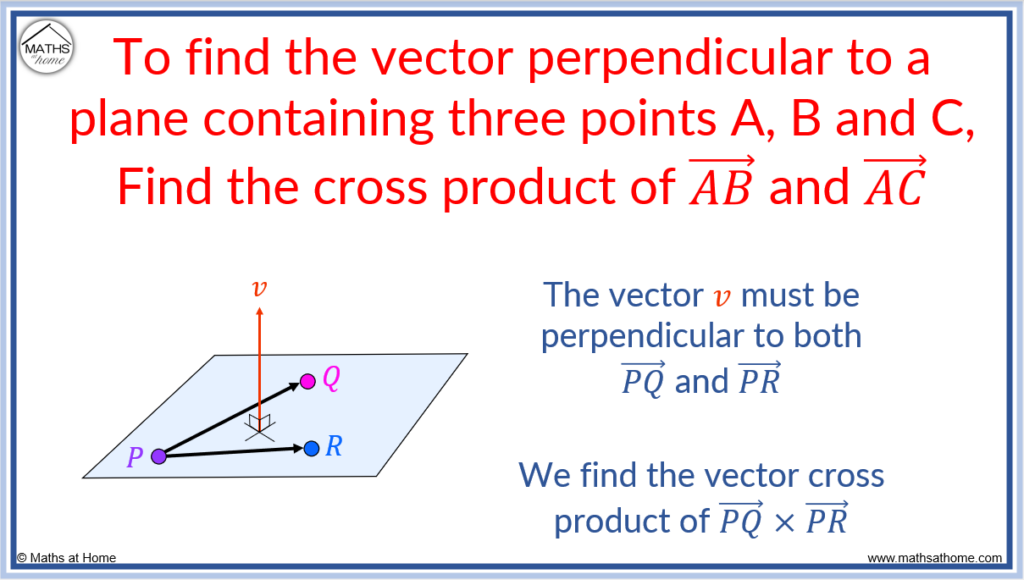
To find a vector perpendicular to a plane from three given points A, B and C:
- Calculate the vectors AB and AC.
- Calculate the cross product of the vectors AB and AC.
A plane is a flat surface that extends forever with zero thickness. A plane can be defined if the location of three points on the plane are known.
The vector perpendicular to a plane is one which intersects the plane at 90 degrees. Alternate names for this are the normal vector or orthogonal vector. These names will be used interchangeably throughout.
The perpendicular vector is at right-angles to the plane which means that it is also at right-angles with any other vectors that lie on the plane such as and
.
For example, find a vector which is perpendicular to the plane passing through the points P(2, 0, -1), Q(1, 1, 3) and R(0, -1, 2).
Step 1. Calculate the vectors and
In this case we calculate the vectors and
.
To calculate we subtract the coordinates of P from the coordinates of Q.
and therefore
.
To calculate we subtract the coordinates of P from the coordinates of R.
and therefore
.

Step 2. Calculate the cross product of the vectors and
In this case we calculate the cross product of the vectors and
.
The result of the cross product will be the the vector that is normal to the plane.
This is because the cross product of two vectors is perpendicular to the two vectors. Since the two vectors and
lie in the plane, any vector perpendicular to both of these vectors will also be perpendicular to the plane.
The cross product of and
is found by writing them above each other like so
.
To find the i component of the cross product, we first cover up the values in the i column and write down the remaining numbers. We will find the determinant of the remaining matrix.
Covering the i column, we are left with the determinant of .


To find the j component, we cover the j column and we are left with the determinant of .
Notice we place a negative sign in front of this determinant. The i and k components do not have this but the j component does. This is part of the cross product calculation method.
To find the k component, we cover the k column and are left with the determinant of .


The cross product of and
is therefore given as:
We now evaluate the determinants in each component of the vector.
To calculate the determinants in each matrix , multiply the top left number by the bottom right number and then subtract the top right number multiplied by the bottom left number.
- For the i component:
- For the j component:
- For the k component:
Therefore the vector normal to the plane is .
This can be written as .

Vector Normal to a Plane Formula
The formula for a vector normal to the plane ax+by+cz=d is n=<a, b, c>.
The vector normal to the plane

How to Find a Vector Normal to a Plane from its Equation
The vector normal to the plane ax+by+cz=d is equal to n=(a, b, c).
For example, the vector normal to the plane 3x+y-2z=12 is given by n=(3, 1, -2).
The coefficients of x, y and z in the equation of the plane form the i, j and k components of the normal vector.
The constant term of the equation of the plane does not affect the normal vector. This is because the constant term of the plane equation does not affect the orientation of the plane, rather it just affects its absolute position. The normal vector is only dependent of the orientation of the plane.

The i component of the normal vector is given by the x coefficient.
We have 3x and so, the i component is 3.
The j component of the normal vector is given by the y coefficient.
We have y, which is the same as 1y and so, the j component is 1.
The k component of the normal vector is given by the z coefficient.
We have -2z and so, the k component is -2.
Here are some further examples of finding the normal vector to a plane from the equation.
| Equation of the Plane | Normal Vector to the Plane |
| 2x + 5y + 3z = 17 | <2, 5, 3> |
| 3x – 2y – 5y = – 2 | <3, -2, -5> |
| x + y + z = 5 | <1, 1, 1> |
| 4x – 3z = 10 | <4, 0, -3> |
| -2x + 5y – z + 10 = 0 | <-2, 5, -1> |
How to Find a Unit Vector Perpendicular to a Plane
The unit vector normal to the plane ax+by+cz=d is given by n=<a, b, c>/√(a2+b2+c2).
The formula for the unit vector normal to the plane

For example, find the unit vector normal to the plane .
In this example we have the following values which can be substituted into the formula :
- a = 5
- b = 1
- c = -3
Therefore the unit vector normal to the plane is .
This simplifies to .
This can be written as or
.
Vector Perpendicular to the xy Plane
The axis perpendicular to the xy plane is the z plane and so the unit vector perpendicular to the xy plane is ±k.
Vector Perpendicular to the yz Plane
The axis perpendicular to the yz plane is the x plane and so the unit vector perpendicular to the yz plane is ±i.
Vector Perpendicular to the xz Plane
The axis perpendicular to the xz plane is the y plane and so the unit vector perpendicular to the xz plane is ±j.
How to Find the Equation of a Plane from the Normal Vector and a Point
If a plane has a normal vector of <a, b, c> and passes through the point (p, q, r) then it has the cartesian equation of ax+by+cy=d, where d = ap+bq+cr.

For example:
Find the equation of the plane with normal vector which passes through the point
.
From the normal vector:
- a = 2
- b = 1
- c = 3
From the point on the plane:
- p = -1
- q = 1
- r = 2
We substitute these values into the formula for the equation of the plane: , where
.
First we calculate to find that
Then the equation of the plane is found as
.
Proof of the Equation of a Plane from a Normal and a Point
r is the position vector of any point on the plane and a is the position vector of a known point on the plane.
Therefore describes any vector on the plane from the known point a to any point r.
n is perpendicular to any vector in the plane therefore the dot product of n and any vector on the plane is equal to zero.
This can be rearranged to give
If ,
and
, then the equation
becomes:
This can be written as where
