Video Lesson: How to Calculate the Magnitude and Direction of a Vector
How to Calculate the Magnitude of a Vector
The magnitude of a vector is a measure of its size or length. To calculate the magnitude, use the formula |v| = √(x2 + y2) where x and y are the horizontal and vertical components of the vector respectively.
Formula for calculating the magnitude of a vector
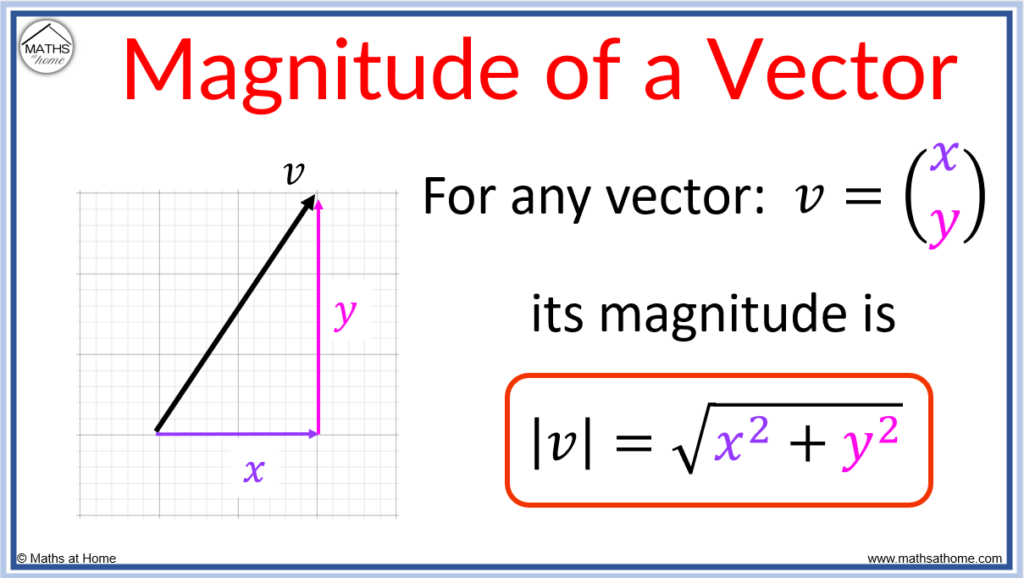
The magnitude of a vector is equal to its length and is a scalar quantity. The magnitude does not describe the direction of the vector.
The magnitude of a vector cannot be negative. All vector magnitudes are positive except for the zero vector which has a magnitude of zero.
How to Calculate the Magnitude of a 2D Vector
The magnitude of a 2D vector is calculated with |v| = √(x2 + y2), where x and y are the components of the vector.
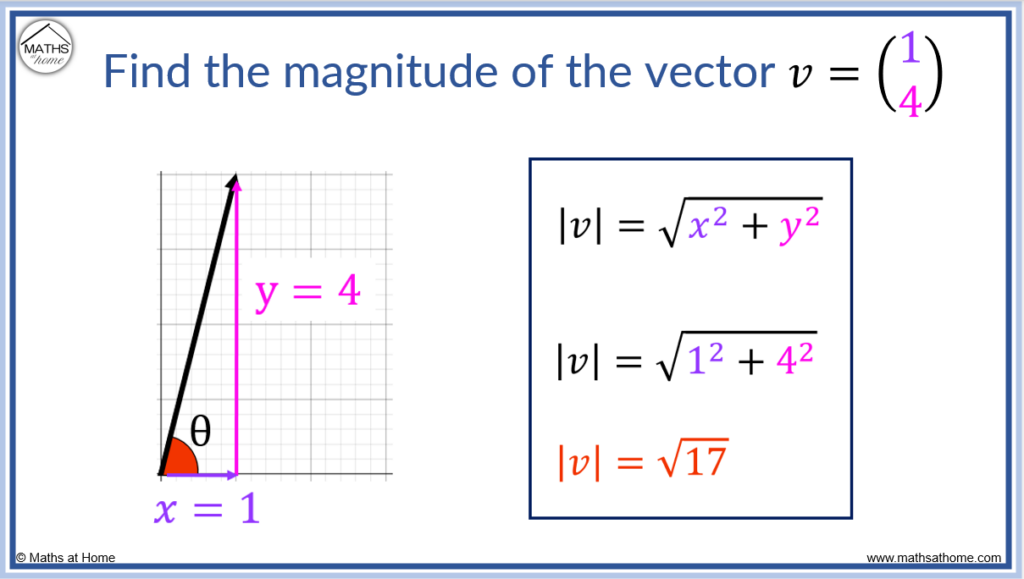
For example, the magnitude of the vector v=(1, 4) is |v| = √(12 + 42) = √17.
The square root of 17 is approximately 4.12 and so, the length of the vector (1, 4) is approximately 4.12.
It is common to leave the magnitude of a vector written as a surd inside the square root in exact form.
Here are some examples of how to calculate the magnitude of a 2 dimensional vector:
| Vector | Magnitude Calculation | Magnitude |
| (5, 1) | √(52+12) | √26 |
| (3, 4) | √(32+42) | 5 |
| (0, 0) | √(02+02) | 0 |
| (-1, -2) | √((-1)2+(-2)2) | √5 |
| (2, 2) | √(22+22) | √8 |
How to Calculate the Magnitude of a 3D Vector
To calculate the magnitude of a 3D vector v=(x, y, z), use the formula |v| = √(x2+y2+z2).
For example, the magnitude of the 3D vector (2, -1, 3) is √(22+(-1)2+32) which equals √14.


The magnitude of a 3 dimensional vector is calculated using the Pythagorean theorem in the same way as a 2D vector but it involves one extra z component.
- x is the x-component of the vector
- y is the y-component of the vector
- z is the z-component of the vector
Formula for the magnitude of a 3 dimensional vector
Here are some examples of calculating the magnitude of a 3D vector:
| Vector | Magnitude Calculation | Magnitude |
| (1, 3, 5) | √(12+32+52) | √35 |
| (3, 0, 1) | √(32+02+12) | √10 |
| (-1, -2, -3) | √((-1)2+(-2)2+(-3)2) | √14 |
| (0,0,0) | √(02+02+02) | 0 |
| (10, 10, 10) | √(102+102+102) | √300 |
How to Calculate the Direction of a Vector
To calculate the direction of the vector v = (x, y), use the formula θ = arctan(y/x).
For vectors in quadrant 1, the direction is θ, in quadrant 2 the direction is 180° – θ, in quadrant 3 the direction is 180° + θ and in quadrant 4 the direction is 360° – θ.

The direction of a vector is the angle measured counter-clockwise from the positive x-axis direction. The angle θ is the angle made between the x and y components of the vector.
Therefore the direction of the vector depends on the quadrant that the vector is in.

How to Calculate the Direction of a 2D Vector
Formula for the direction of a 2 dimension vector
For example, calculate the direction of the vector v = (1, 4).
- The x component is 1
- The y component is 4
Therefore and so,
.
Since the vector is in the first quadrant, is the direction of the vector.

Calculate the direction of the vector (-2, -3).
- The x component of the vector is -2
- The y component of the vector is -3
The vector is in quadrant two and therefore, the direction is equal to .
and so,
.
Evaluating this, and therefore the direction is
.

Vector Magnitude and Direction Calculator
The following calculator will calculate the magnitude and direction of a vector.
For any vector , enter the x component and y component in the calculator below to obtain the magnitiude and direction.
