How to Find the Vector Between Two Points

Video Lesson: How to Find the Vector Between Two Points

How to Find the Vector Between Two Points

To find the vector between two points, subtract the coordinates of the initial point from the coordinates of the final point.

For example, the vector from A(2, 3) to B(4, 0) is found by subtracting A from B with the calculation (4-2, 0-3) to obtain (2, -3).

It is important to note the order of the subtraction.

In the calculation of any vector A B right arrow, we subtract the coordinates of A from the coordinates of B. Subtract the first set of coordinates listed from the second set of coordinates.

example of how to find the vector between two points

Point A has the coordinates (2, 3) and point B has the coordinates (4, 0).

The vector of O A right arrow is simply the vector from the origin to point A. It contains the same values as the coordinates of point A.

Therefore the vector O A right arrow equals the 2 by 1 column matrix 2 3 and O B right arrow equals the 2 by 1 column matrix 4 0.

The vector A B right arrow is the difference between A and B. It describes how to travel from point A to point B.

We calculate it using the formula: A B right arrow equals O B right arrow minus O A right arrow.

When we subtract vectors, we subtract the i components from each other and the j components from each other separately.

That is, we subtract the numbers on the tops of the vector and then the numbers on the bottom of the vector.

Therefore A B right arrow equals the 2 by 1 column matrix Row 1: 4 minus 2 Row 2: 0 minus 3 which is evaluated to be A B right arrow equals the 2 by 1 column matrix 2 negative 3.

We can see the vector from A to B in the diagram above shown with the red arrow. We can see from the diagram that this matches the calculated vector because it travels 2 right and 3 down.

Here is another example of calculating a vector between two points.

Given the points P(4, -1) and Q(-3, 0), find the vector P Q right arrow.

Since the vector is directed from P to Q, we subtract P from Q.

We subtract the 2 by 1 column matrix negative 3 0 minus the 2 by 1 column matrix 4 negative 1 to obtain the 2 by 1 column matrix Row 1: negative 3 minus 4 Row 2: 0 minus negative 1.

Evaluating this, P Q right arrow equals the 2 by 1 column matrix negative 7 1.

example of how to calculate a vector from A to B

The vector from A to B is equal to the distance of each component from point A to point B.

An alternative method to calculate the vector from A to B is to work out the values that must be added to point A to get to point B.

We think ‘what must be added to the first set of coordinates to obtain the second set of coordinates’.

In the above example, we need to get from the 2 by 1 column matrix 4 negative 1 to the 2 by 1 column matrix negative 3 0.

We must subtract 7 from 4 to obtain -3 and we must add 1 to -1 to obtain 0.

the 2 by 1 column matrix 4 negative 1 plus the 2 by 1 column matrix negative 7 1 equals the 2 by 1 column matrix negative 3 0

Therefore the vector P Q right arrow equals the 2 by 1 column matrix negative 7 1.

How to Find the Vector Between Two Points in 3D

To find a vector between two points in 3D, subtract the initial point from the final point. The vector from point A(a1, a2, a3) to point B(b1, b2, b3) is given by (b1 – a1, b2 – a2 , b3 – a3).

Simply subtract the x coordinates of point A from the x coordinates of point B, the y coordinates of point A from the y coordinates of point B and the z coordinates of point A from the z coordinates of point B

how to find the vector between two points in 3d

For example, find the vector from A(3, 1, 2) to B(-2, 0, 3).

  • For the i component of the vector: -2 – 3 = -5
  • For the j component of the vector: 0 – 1 = -1
  • For the k component of the vector: 3 – 2 = 1

The vector 3D vector from A to B is A B right arrow equals the 3 by 1 column matrix negative 5 negative 1 1.

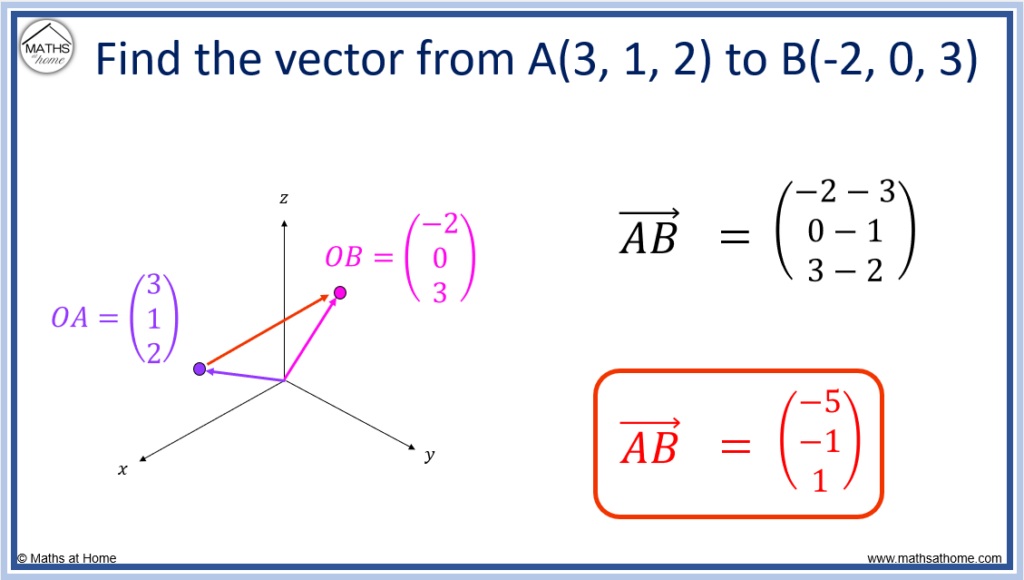
how to calculate the vector between two points in 3d example

Again, we can also calculate this by thinking ‘what vector must be added to the first point of the 3 by 1 column matrix 3 1 2 to obtain the second point of the 3 by 1 column matrix negative 2 0 3?’

We know that the 3 by 1 column matrix 3 1 2 plus the 3 by 1 column matrix negative 5 negative 1 1 equals the 3 by 1 column matrix negative 2 0 3 and so the vector A B equals right arrow times the 3 by 1 column matrix negative 5 negative 1 1.

Vector Between Two Points Formula

The formula to calculate a vector from A to B is (A→B) = (O→B) – (O→A). In words this means to subtract the coordinates of point B from point A.

A B right arrow equals O B right arrow minus O A right arrow

The formula for the vector from A to B

The vector O A right arrow is simply made up of the coordinates of point A, which are the 2 by 1 column matrix a. sub 1 a. sub 2 and similarly, the vector O B right arrow is the 2 by 1 column matrix b sub 1 b sub 2.

Therefore, the formula for the vector A B right arrow can be written in 2 dimensions as:

A B right arrow equals the 2 by 1 column matrix Row 1: b sub 1 minus a. sub 1 Row 2: b sub 2 minus a. sub 2

The formula for the vector from A to B in 2D

In 3 dimensions, the vector A B right arrow

A B equals right arrow times the 3 by 1 column matrix Row 1: b sub 1 minus a. sub 1 Row 2: b sub 2 minus a. sub 2 Row 3: b sub 3 minus a. sub 3

The formula for the vector from A to B in 3D
formula for the vector between two points

Examples of Calculating the Vector Between Two Points

Here are some examples of calculating the vector A B right arrow between two points A and B in 2 dimensions.

The i component of the vector is found by subtracting the x coordinate of A from the x coordinate of B.

The j component of the vector is found by subtracting the y coordinate of A from the y coordinate of B.

Point APoint Bi component calculationj component calculationVector from A to B
(0,0)(4, 3)4 – 0 = 43 – 0 = 3(4, 3)
(1, 2)(8, 3)8 – 1 = 73 – 2 = 1(7, 1)
(6, 3)(3, 1)3 – 6 = -31 – 3 = -2(-3, -2)
(-5, -2)(3, 0)3 – -5 = 80 – -2 = 2(8, 2)
(-3, 4)(-1, -2) -1 – -3 = 2-2 – 4 = -6(2, -6)

Here are some examples of calculating the vector A B right arrow between two points A and B in 3 dimensions.

The i component of the vector is found by subtracting the x coordinate of A from the x coordinate of B.

The j component of the vector is found by subtracting the y coordinate of A from the y coordinate of B.

Point APoint Bi component calculationj component calculationk component calculationVector from A to B
(0, 0, 0)(1, 3, 2)1 – 0 = 13 – 0 = 32 – 0 = 2(1, 3, 2)
(1, 5, 3)(4, 8, 6)4 – 1 = 38 – 5 = 36 – 3 = 3(3, 3, 3)
(8, 4, 1)(2, 3, 1)2 – 8 = -63 – 4 = -11 – 1 = 0(-6, -1, 0)
(-1, 0, -2)(3, 2, 1)3 – -1 = 42 – 0 = 21 – -2 = 3(4, 2, 3)
(-5, -1, -3)(-2, -4, -9)-2 – -5 = 3-4 – -1 = -3-9 – -3 = -6(3, -3, -6)

Vector Between Two Points Calculator

Below is a calculator to find the vector between two points.

Select whether the vector is in 2 or 3 dimensions and then enter the x, y and z coordinates of each below.

The calculator will then calculate the i, j and k components of the vector from A to B.