Equation of a Circle Video Lessons
How to Find the Equation of a Circle
How to Graph a Circle
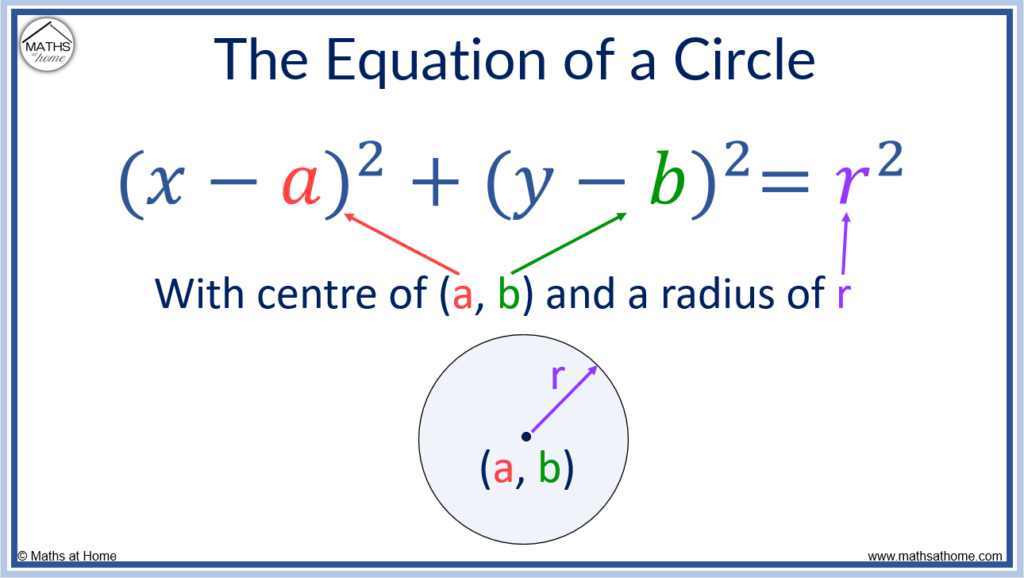
What is the Equation of a Circle?
The standard form equation of a circle is (𝑥 – a)2 + (y – b)2 = r2, where (a,b) is the centre and r is the radius. For example, a circle with centre (5, -3) and radius 3 has the equation (𝑥 – 5)2 + (y + 3)2 = 9.

(𝑥 – a)2 + (y – b)2 = r2 is known as the standard form of the equation of a circle.
This is because the centre and radius of the circle can be easily read from the equation and they can be easily substituted in to make the equation.
The equation of a circle is not a function. This is because circle equations do not pass the ‘vertical line test’ required for functions. Instead we say that the equation of a circle is a relation.
To be a function, any given input (𝑥 value) must have exactly one output (y value). However for most 𝑥 values, circles produce two outputs. Therefore a circle is not a function.

We can see in this example of (𝑥 – 5)2 + (y – 5)2 = 16 that the single input of 𝑥 = 5 gives two outputs: y = 1 and y = 9.
It is possible to rearrange the equation of a circle in terms of 𝑥 or y. In this case, to ensure that it remains a function, we must only consider the positive values of the square root.
In terms of y, the equation of a circle is .
In terms of 𝑥, the equation of a circle is
How to Find the Equation of a Circle
To find the equation of a circle:- Find the coordinates of the centre of the circle
- Find the length of the radius: r
- Substitute these values into the equation of a circle: (𝑥 – a)2 + (y – b)2 = r2
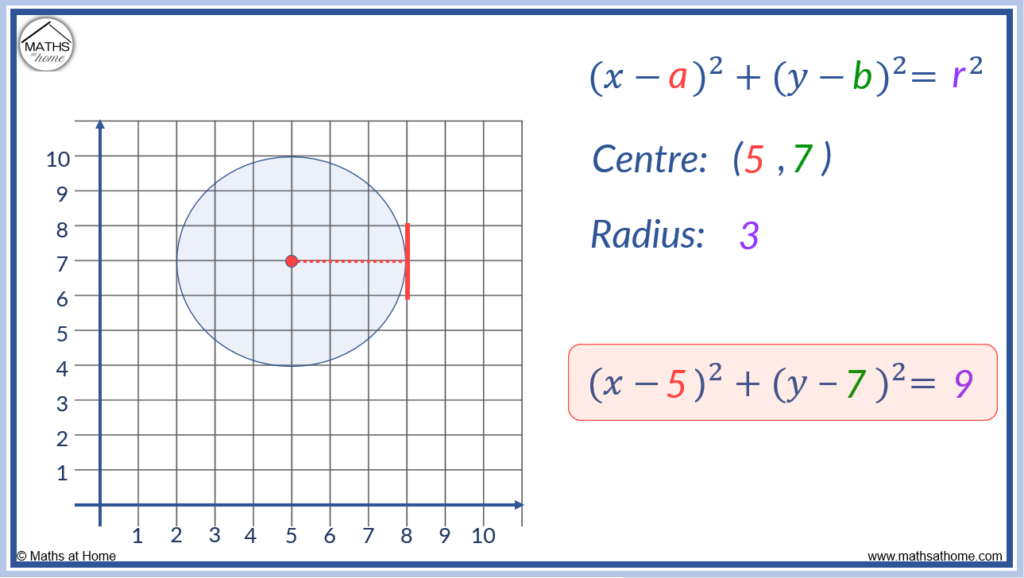
For example, find the equation of the circle with centre (5,7) and radius 3.
The standard equation of a circle is (𝑥 – a)2 + (y – b)2 = r2, where:
- ‘a’ is the 𝑥-coordinate of the centre of the circle
- ‘b’ is the y-coordinate of the centre of the circle
- ‘r’ is the radius of the circle
If the centre is (5,7) then ‘a’ = 5 and ‘b’ = 7.
If the radius is 3 then r = 3 and r2 = 9.
The equation of the circle, (𝑥 – a)2 + (y – b)2 = r2, becomes (𝑥 – 5)2 + (y – 7)2 = 9.
For example, find the equation of the circle with centre (-6, -3) and radius 2.
In this example, ‘a’ = -6, ‘b’ = -3 and r = 2
The values of ‘a’ and ‘b’ are both negative. This means that when they are subtracted, they become positive. Subtracting a negative number is the same as adding it.
Therefore (𝑥 – a)2 + (y – b)2 = r2, becomes (𝑥 + 6)2 + (y + 3)2 = 4.

How to Graph a Circle
To graph a circle, read the coordinates of the centre, (a,b) and the radius, r from the circle equation (𝑥 – a)2 + (y – b)2 = r2. First plot the centre coordinates and from here, use the radius length to find the outer points on the circle.
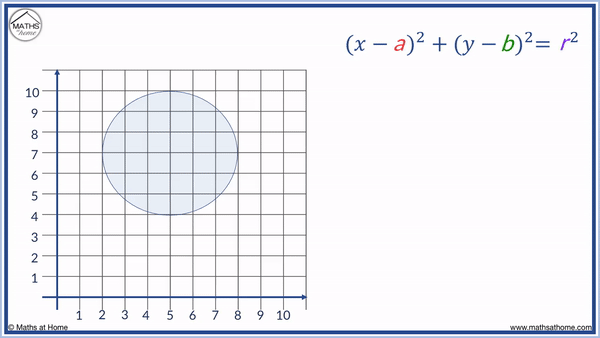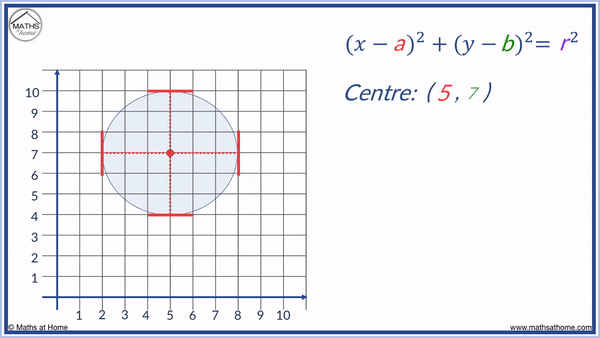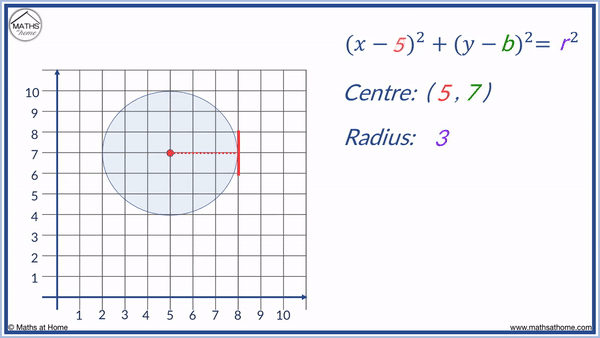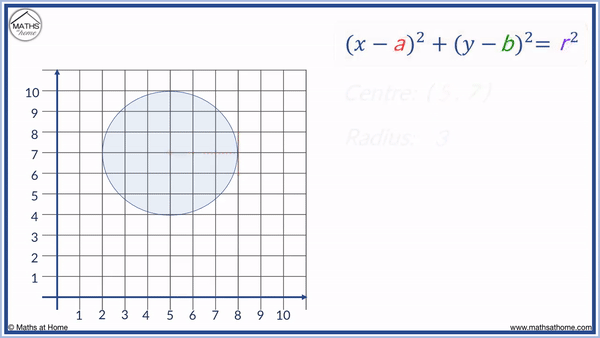
For example, graph the circle with equation (𝑥 – 7)2 + (y – 4)2 = 4
In this example, the centre is (7, 4).
We first plot this centre coordinate by finding 7 on the 𝑥-axis and 4 on the y-axis.
To draw the circle, it helps to form a cross using vertical and horizontal lines coming out from the centre that are each as long as the radius.
We draw lines that are 2 long because the radius of this circle is 2.

We can then graph the circle using a compass so that the circle passes through these outer points.
The Equation of a Circle with a Centre at the Origin
The equation of a circle with its centre at the origin and a radius of r has the equation 𝑥2 + y2 = r2. For example, a circle with centre (0,0) and radius 6 has the equation 𝑥2 + y2 = 36.

The origin is where the 𝑥 and y axes meet and it has the coordinates (0,0).
If a circle has a centre at the origin, then centre of the circle is (0,0). Therefore ‘a’ = 0 and ‘b’ = 0 and the standard equation of a circle becomes (𝑥 – a)2 + (y – b)2 = r2 to (𝑥 – 0)2 + (y – 0)2 = r2.
This reduces to 𝑥2 + y2 = r2.
To find the equation of a circle with a centre at the origin, find its radius and substitute it into 𝑥2 + y2 = r2 .
How to Write the Equation of a Circle in General Form
The general form of the circle equation is 𝑥2 + a𝑥 + y2 + by + c= 0. To write the equation of a circle in general form, simply expand the two brackets in its standard form (𝑥 – a)2 + (y – b)2 = r2. Then collect like terms.
For example write the equation of a circle with centre (2, 0) and radius 1 in general form
Step 1. Write the equation of a circle in standard form using the centre and radius.
The standard form of the circle equation can be written as (𝑥 – a)2 + (y – b)2 = r2 , where the centre is (a, b) and the radius is r.
With a centre of (2, 0) and radius of 1, the circle equation becomes (𝑥 – 2)2 + y2 = 1.
Step 2. Expand the brackets in the standard form of the equation.
(𝑥 – 2)2 + y2 = 1 means (𝑥 – 2)(𝑥 – 2) + y2 = 1.
Expanding the brackets (𝑥 – 2)(𝑥 – 2), we have 𝑥2 – 4𝑥 + 4.
Therefore (𝑥 – 2)(𝑥 – 2) + y2 = 1 becomes 𝑥2 – 4𝑥 + 4 + y2 = 1.
Step 3. Collect like terms
We now collect like terms, which means to add up all of the 𝑥2 terms, all of the y2 terms and all of the constant terms.
We can do this by subtracting 1 from both sides of the equation.
𝑥2 – 4𝑥 + 4 + y2 = 1 becomes 𝑥2 – 4𝑥 + y2 + 3= 0.
The expanded form of the equation of the circle is 𝑥2 – 4𝑥 + y2 + 3= 0.
We tend to write the 𝑥 terms first, then the y terms and then the constant terms. We also set the equation equal to zero.
The advantage of the general form of the circle equation is that it is easier to substitute values of 𝑥 and y into. This makes it an easier choice for finding particular coordinates on the circle or axis intercepts.
The advantage of the standard form of the circle equation is that we can easily read off the coordinates of the centre of the circle and its radius. When written as (𝑥 – a)2 + (y – b)2 = r2, (a,b) is the centre and r is the radius.
How to Write the Equation of a Circle in Standard Form
The equation of a circle in standard form is (𝑥 – a)2 + (y – b)2 = r2. To write the equation of a circle in standard form, collect the 𝑥2 and 𝑥 terms together, the y2 and y terms together and complete the square with them separately. Then move any constant terms to the other side of the equals sign.
For example, find the centre and radius of the circle with equation 𝑥2 + y2 + 4𝑥 – 8y + 3 = 0
Step 1. Collect the 𝑥 terms and y terms together
We move the 𝑥2 and 𝑥 terms next to each other and the y2 and y terms next to each other so that:
𝑥2 + y2 + 4𝑥 – 8y + 3 = 0 becomes 𝑥2 + 4𝑥 + y2 – 8y + 3 = 0
Step 2. Complete the square for the 𝑥 terms and the y terms
We will complete the square for 𝑥2 + 4𝑥 and then complete the square for y2 – 8y.
To complete the square for 𝑥2 + 4𝑥, we start with (𝑥 + )2.
To find the number that goes in the brackets with the 𝑥, we halve the coefficient of 4𝑥. Half of 4 is 2 and so we get (𝑥 + 2)2.
Finally we subtract this number squared. 2 squared is 4 and so we get: (𝑥 + 2)2 – 4.
Now we will complete the square for y2 – 8y.
To complete the square for y2 – 8y, we start with (y – )2.
To find the number that goes in the brackets with the y, we halve the coefficient of 8y. Half of 8 is 4 and so we get (y – 4)2.
Finally we subtract this number squared. 4 squared is 16 and so we get: (y – 4)2 – 16.
Step 3. Substitute these expressions into the original equation
Completing the square for 𝑥2 + 4𝑥 gave us (𝑥 + 2)2 – 4.
Completing the square for y2 – 8y gave us (y – 4)2 – 16.
We substitute these expressions into the original equation from step 1: 𝑥2 + 4𝑥 + y2 – 8y + 3 = 0.
This becomes (𝑥 + 2)2 – 4 + (y – 4)2 – 16 + 3 = 0.
Step 4. Move all constant terms to the right hand side of the equals sign
We can collect the constant terms in (𝑥 + 2)2 – 4 + (y – 4)2 – 16 + 3 = 0 so this becomes
(𝑥 + 2)2 + (y – 4)2 – 17 = 0
We then add 17 to both sides of the equation to get:
(𝑥 + 2)2 + (y – 4)2 = 17
The equation of the circle has now been converted to standard form. When written in standard form we can easily read the centre and radius of the circle.
The centre is (-2, 4) and the radius is √17.
Equation of a Circle Derivation
The equation of a circle (𝑥 – a)2 + (y – b)2 = r2 can be derived from the equation for the distance between two points. Simply substitute the coordinates of (a,b) as the centre of the circle and r as the radius of the circle and then square both sides.
Here is the algebraic proof of the equation of a circle.

Using Pythagoras’ theorem, the distance between two points with coordinates (𝑥1,y1) and (𝑥2,y2) is:
For a circle, the two points in question are the centre and a point on the circle radius.
This means that (𝑥1,y1) becomes the centre: (a, b)
(𝑥2,y2) is any point on the radius of the circle, which is just (𝑥,y).
The distance between the points, d, is therefore just the radius, r.
We can then square both sides of the equation to find the standard equation of a circle:
(𝑥 – a)2 + (y – b)2 = r2
How to Find the 𝑥 and y Intercepts for a Circle
To find the 𝑥 intercepts of a circle, substitute y = 0 into the circle equation. Then solve the resulting quadratic equation for 𝑥. To find the y intercepts of a circle, substitute 𝑥 = 0 into the circle equation and solve the resulting quadratic equation for y.
There may be 0, 1 or 2 axis intercepts depending on the equation of the circle.
For example, find the 𝑥-axis intercepts of (𝑥 – 5)2 + (y + 3)2 = 16
Step 1. Substitute y = 0 into the circle equation.
(𝑥 – 5)2 + (y + 3)2 = 16 becomes (𝑥 – 5)2 + 32 = 16.
Step 2. Rearrange this quadratic equation so that it is equal to zero.
(𝑥 – 5)2 + 32 = 16 can be written as (𝑥 – 5)(𝑥 – 5) + 32 = 16 and expanding the brackets we get 𝑥2 – 10𝑥 + 25 + 32 = 16.
Collecting the constant terms, we get: 𝑥2 – 10𝑥 + 18 = 0.
Step 3. Solve the quadratic equation
Using the quadratic formula, , where a = 1, b = -10 and c = 18.
The quadratic formula becomes .
and 𝑥 = 2.35 and 𝑥 = 7.65.
Therefore the 𝑥-axis intercepts of the circle are found at 𝑥 = 2.35 and 𝑥 = 7.65.

An alternative method to find the 𝑥 or y intercepts is to simply graph the circle and observe where it crosses the axes. However this will only result in an approximation which will need verifying using the algebraic method above.
The quadratic equation had two solutions and so, the circle had 2 axis intercepts.
If the quadratic equation has no solutions, this means that the circle does not have axis intercepts.
If the quadratic equation has just one solution, this means that the circle has one axis intercept. To have one axis intercept, the circle will be touching the axis.
For example, find the y-axis intercepts of (𝑥 + 3)2 + (y – 5)2 = 9
Step 1. Substitute 𝑥 = 0 into the circle equation
(𝑥 + 3)2 + (y – 5)2 = 9 becomes 32 + (y – 5)2 = 9.
Step 2. Rearrange this quadratic equation so that it is equal to zero.
32 + (y – 5)2 = 9 can be written as 32 + (y – 5)(y – 5) = 9 and expanding the brackets we get 9 + y2 – 10y + 25 = 9.
Subtracting 9 from both sides, we get: y2 – 10y + 25 = 0.
Step 3. Solve the quadratic equation
y2 – 10y + 25 = 0 can factorise to (y – 5)(y – 5) = 0.
There is only one solution to this quadratic equation. Setting the factor ( y – 5) = 0, we get y = 5.

We can see that there is only one y-axis intercept for this circle equation.
If a circle is just touching the axis, there is only one axis intercept. This means that there is only one solution to the quadratic equation created when setting 𝑥 or y to 0.
The Parametric Form of a Circle
The parametric form of the circle equation, 𝑥2 + y2 = r2 , is 𝑥 = r cosθ, y = r sinθ. If the circle is translated a units right and b units up, the circle equation (𝑥 – a)2 + (y – b)2 = r2 can be written parametrically as 𝑥 = a + r cosθ, y = b+ r sinθ.
To derive the parametric equations of a circle, start with basic trigonometry for a right-angled triangle.
For any given right-angled triangle, the opposite side is equal to the hypotenuse multiplied by sine of the angle.
The adjacent side is equal to the hypotenuse multiplied by the cosine of the angle.

A right-angled triangle can be drawn from the centre of a circle to its edge, so that the radius of the circle is the hypotenuse of the triangle.
Therefore the 𝑥 coordinate of any point on the outside of the circle is the same as the adjacent side of the triangle and the y coordinate of the same point is the same as the opposite side of the triangle.
We can substitute the hypotenuse equal to r, the opposite equal to y and the adjacent equal to 𝑥.
Therefore, we get two parametric equations for the coordinates of any point on the circle:
𝑥 = r cosθ, y = r sinθ
As θ changes, we rotate to a new coordinate on the circle. Increasing θ from 0 to 360° (2π), we obtain coordinates that form the complete circumference of the circle.
We say that θ is the parameter in these parametric equations.
The parametric equations for a circle with centre (a, b) and radius r are:
𝑥 = a + r cosθ, y = b+ r sinθ
We simply add ‘a’ to the 𝑥 coordinate to move it ‘a’ units right.
We add ‘b’ to the y coordinate to move it ‘b’ units up.
The Equation of a Circle in Complex Form
On the complex plane, |z| represents the distance of the complex number z from the origin. Therefore the equation of any circle radius r, with the origin as its centre can be written as |z| = r. For a circle with centre z0, where a is also a complex number, the equation is |z – z0| = r.
For example, a circle with centre (4, 3) and radius 2 can be represented with complex numbers.
On the complex plane (4, 3) means 4 in real numbers and 3 in imaginary numbers. (4, 3) is equivalent to 4 + 3i.
The centre, z0 = 4 + 3i.
The radius, r is 2.
Therefore |z – z0| = r becomes |z – (4 + 3i)| = 2.

