Pythagoras’ Theorem Video Lessons
Pythagoras – Finding the Hypotenuse (Longer Side)
Pythagoras – Finding One of the Shorter Sides
What is Pythagoras’ Theorem
Pythagoras’ theorem is a2 + b2 = c2, where a and b are the two shorter sides of a right-angled triangle and c is the longest side, opposite the right angle. The theorem is used to find a missing side of a right-angled triangle when the other two sides are known.

Pythagoras’ theorem is used to determine a missing side of a right-angled triangle when 2 other sides are known.
To use Pythagoras’ theorem, the triangle must contain a right-angle and 2 side lengths must be known.
How to Do Pythagoras’ Theorem
To use Pythagoras’ Theorem:- Square the two known sides.
- If finding the hypotenuse, add the numbers from step 1 together.
- If finding one of the shorter sides, find the difference between the numbers from step 1.
- Square root this result.
For example, find the missing hypotenuse of this triangle
This triangle has two shorter sides of length 5 cm and 9 cm.
The two shorter sides are labelled as ‘a’ and ‘b’. It does not matter which is ‘a’ or which is ‘b’.
‘c’ is labelled as the hypotenuse. In other words, ‘c’ is always the longest side of a right-angled triangle.
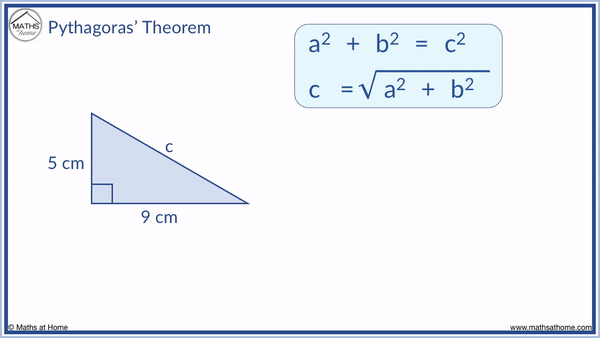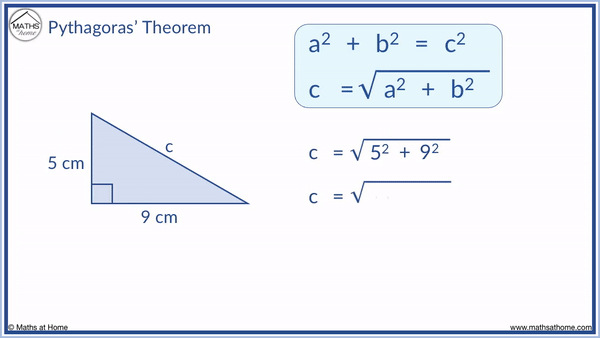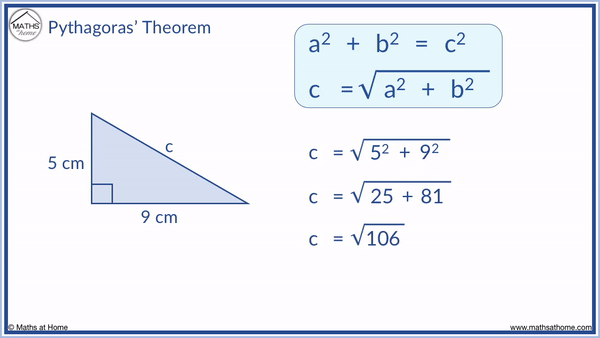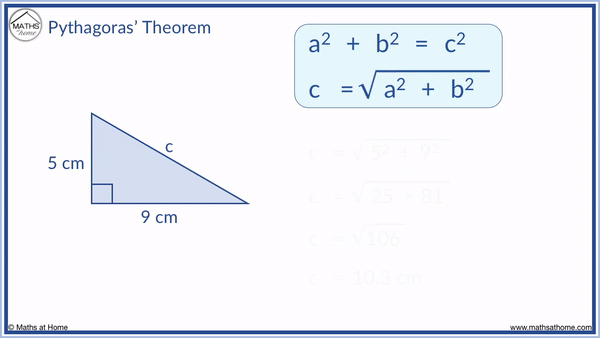
Pythagoras’ theorem is a2 + b2 = c2. This can be rearranged for ‘c’ by taking the square root of both sides of the equation. The formula for a missing hypotenuse becomes:
First square the two shorter sides of 5 and 9 to get a2 = 25 and b2 = 81.
Next we add a2 and b2 together. 25 + 81 = 106.
Finally we square root this result.
√106 = 10.3 to 1 decimal place.
To check the Pythagorean theorem calculation, the calculated hypotenuse should be larger than the two shorter sides. 10.3 is larger than both 5 and 9 but not by a very large magnitude. It is therefore less likely that a mistake has been made and our result is more likely to be correct.
For example, find the missing shorter side of this triangle
This triangle has a hypotenuse of 11 cm and one of the shorter sides is 6 cm. We need to find the other shorter side on the base of the triangle.
The hypotenuse, which is the side opposite to the right angle, is always labelled as ‘c’.
Label ‘a’ as the missing shorter side that you wish to find.
Label ‘b’ as the shorter side that you know the length of.

Pythagoras’ theorem is a2 + b2 = c2. This can be rearranged for a shorter side, ‘a’ by subtracting b2 from both sides of the equation to get a2 = c2 – b2. Taking the square root of both sides, the formula for a missing shorter side becomes:
We first square both known sides. c = 11 and b = 6. Therefore, c2 = 121 and b2 = 36.
To work out c2 – b2, we work out 121 – 36. This equals 85.
Finally, we square root this to find the missing side.
√85 = 9.2 to 1 decimal place.
How to Find the Hypotenuse Using Pythagoras
The hypotenuse is the longest side of a right-angled triangle. To find it:- Square the two known sides.
- Add these results together.
- Square root this result.

How to Find the Shorter Side Using Pythagoras
To find one of the shorter sides using Pythagoras:- Square the two known sides
- Of these values, subtract the smaller answer from the larger answer.
- Square root this result.

Pythagoras’ Theorem Calculator
To use Pythagoras’ theorem, you must know the length of two sides of a right-angled triangle.
Enter the two known sides in the solver below and it will automatically calculate the missing side.
Simple Proof of Pythagoras’ Theorem
To prove Pythagoras’ theorem:- Place 4 triangles with sides a, b and c to form a square where each side is made by combining sides a and b.
- Find the area of the outer square: 2 + 2ab + b2.
- Subtract the area of the 4 triangles: 2ab.
- This leaves the area of the inner square: c2.
Pythagoras’ theorem always works for any right-angled triangle because it has been proven algebraically. Several algebraic proofs exist linking the squares of each side of a right-angled triangle.

Step 1. Place 4 triangles with sides a, b and c to form a square where each side is made by combining sides a and b
We take four of these identical triangles and place them so that side a and side b are next to each other, forming a square.
We can also see a diagonal inner square has formed with side lengths of c.

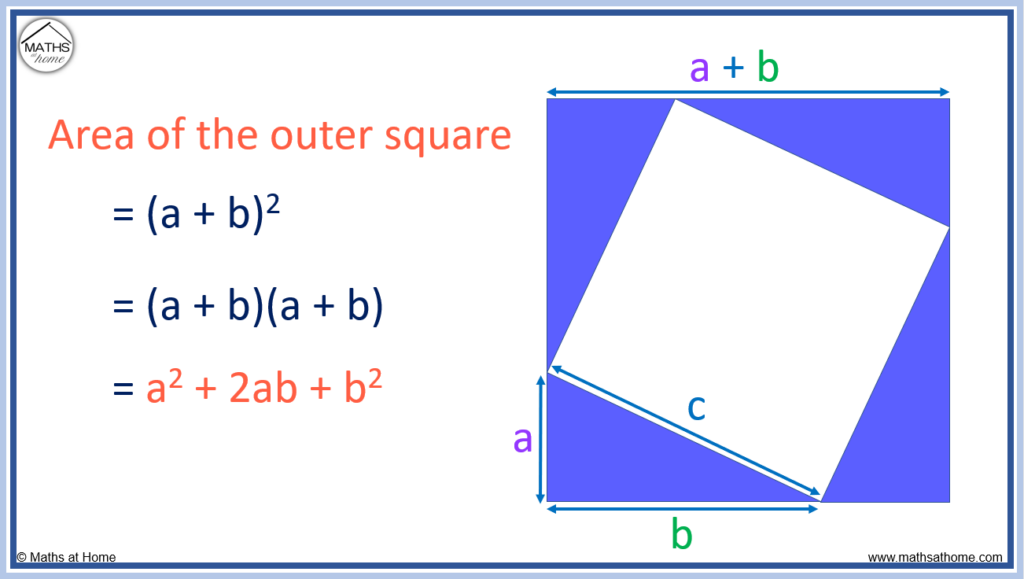
Step 2. Find the area of the outer square
Each side of the outer square is made from sides a and b combined.
Therefore the length of the outer square is (a + b).
Therefore the area of the outer square is (a + b)2.
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2.
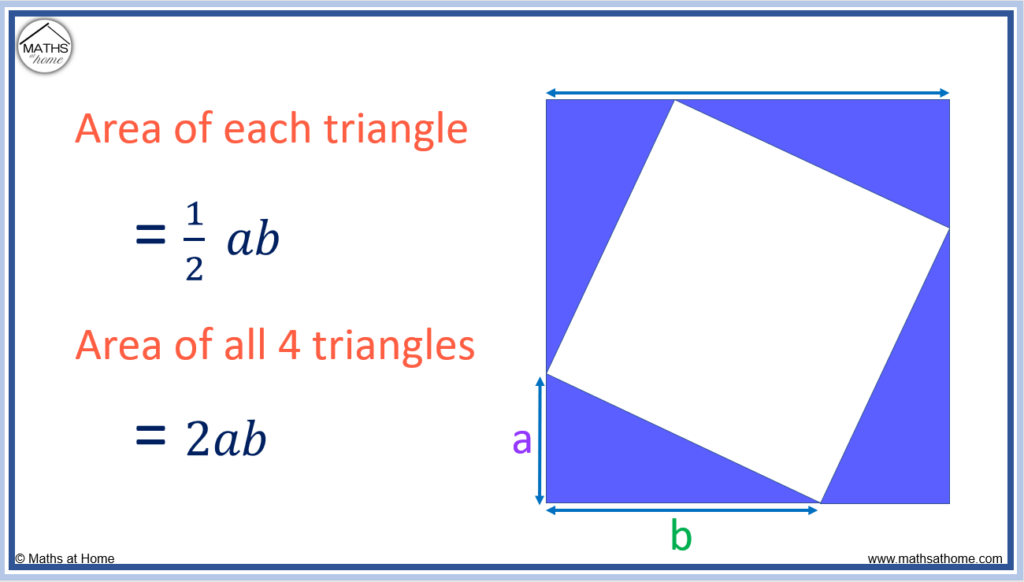
Step 3. Subtract the area of the 4 triangles
Each of the blue triangles has base = b and height = a.
The area of a triangle is .
The area of each triangle is therefore .
Since we have four triangles, the total area of all four triangles is .
This simplifies to 2ab.
Step 4. Subtract the area of the 4 triangles from the area of the outer square to leave the area of the inner square
The area of the outer square subtract the area of the four triangles equals the area of the inner square.
- Area of the outer square = a2 + 2ab + b2
- Area of the 4 triangles = 2ab
- Area of the inner square = c2

The Converse of Pythagoras’ Theorem
The converse of Pythagoras’ theorem states that a triangle is right-angled only if its sides obey Pythagoras’ theorem. That is, if the two smaller sides squared sum to the same value as the largest side squared, the triangle contains a right angle.
Pythagoras’ theorem only works for right-angled triangles. It also must always work if we have a right-angled triangle.
Therefore Pythagoras’ theorem is a perfect method to use to test if a triangle contains a right-angle or not.
Pythagoras’ theorem is often used to find a missing side, when we already know the triangle contains a right angle. The converse of Pythagoras’ theorem is when we already know all three sides but use these to check if there is a right angle in the first place.
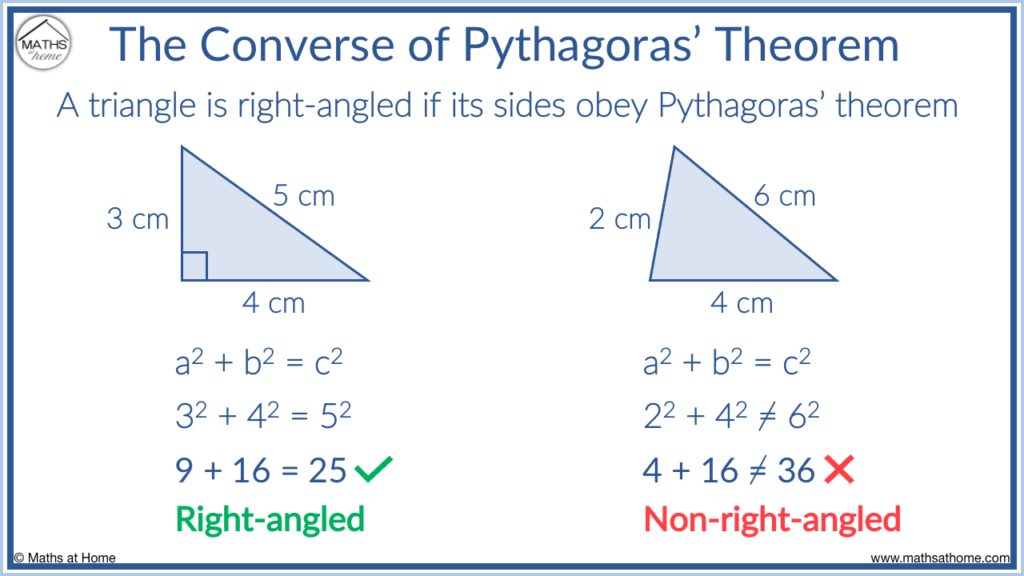
The converse of Pythagoras theorem is used as a test to decide if a triangle contains a right angle or not. All three sides of the triangle must be known to do the test.
For example, the triangle containing side lengths of 3, 4 and 5 does contain a right angle. This is because 32 + 42 = 52.
9 + 16 = 25 and so the triangle satisfies Pythagoras’ theorem and so it must contain a right angle.
For example, the triangle containing side lengths of 2, 4 and 6 does not contain a right angle. This is because 22 + 42 ≠ 62.
4 + 16 ≠ 36 and so the triangle cannot contain a right angle.
How Do You Know When To Use Pythagoras or Trigonometry?
If you need to find a missing angle, you must use trigonometry. If you need to find a missing side, Pythagoras or trigonometry can be used. If you have two known sides in a triangle, use Pythagoras to find the third side. If you know a side and an angle, use trigonometry.

Both Pythagoras’ theorem and trigonometry can be used with right-angled triangles.
To decide whether to use Pythagoras’ theorem or trigonometry, use the following rules:
- To find a missing angle, use trigonometry
- To find a missing side with one known side and one known angle, use trigonometry
- To find a missing side with the other 2 known sides, use Pythagoras

For example, find the missing side on this triangle
To find a missing side, Pythagoras or trigonometry can be used.
Since we know the other 2 side lengths, we know that we use Pythagoras. We would need to have known an angle to use trigonometry.

b = 10 and c = 20
Therefore, b2 = 100 and c2 = 400
Since we are finding a shorter side, we subtract these and then square root the answer.
and so,
The missing side, a = 17.3
For example, find the missing side on this triangle
To find a missing side, Pythagoras or trigonometry can be used.
Since we know one side and know an angle, we use trigonometry. We would need to know the 2 other sides to use Pythagoras.

We want the opposite side and we know the hypotenuse. Using SOHCAHTOA, we will use the SOH ratio since we have H and need O.
O = H × sin(θ) and so,
O = 10 × sin(30) = 5. Therefore the missing side length is 5.
Pythagoras’ Theorem in 3D
Pythagoras’ theorem can be used in 3D problems involving right-angled triangles. Pythagoras equation in 3D tells us that the length of the diagonal of a cuboid is d = √( 𝑥2 + y2 + z2), where 𝑥, y and z are the side lengths of the cuboid.
The diagonal of a cuboid is , where 𝑥, y and z are the side lengths of the cuboid.

We can derive Pythagoras’ theorem in 3D by considering 2 separate right-angled triangles within a cuboid.
We can do Pythagoras in 2D in the pink triangle for the base triangle to find the diagonal base length, c.
We can then use this side length in the green triangle to calculate the diagonal length, d.

For example, use Pythagoras’ theorem to find the diagonal length of a cube with side lengths of 5.

Pythagoras’ theorem in 3D is
In a cube, all sides are the same length and so, 𝑥, y and z are all equal to 5.
The equation becomes
Pythagorean Triples
Pythagorean triples are three integers a, b and c, such that a2 + b2 = c2. For example 3, 4 and 5 form the a Pythagorean triple because 32 + 42 = 52. Pythagorean triples can be found using the formulae of a = m2 – n2, b = 2mn, c = m2 + n2.
List of Pythagorean Triples
Here is a complete list of the first Pythagorean triples:
| (3, 4, 5) | (5, 12, 13) | (6, 8, 10) |
| (7, 24, 25) | (8, 15, 17) | (9, 12, 15) |
| (9, 40, 41) | (10, 24, 26) | (11, 60, 61) |
| (12, 16, 20) | (12, 35, 37) | (13, 84, 85) |
| (14, 48, 50) | (15, 20, 25) | (15, 36, 39) |
There are an infinite number of Pythagorean triples.
Some Pythagorean triples are multiples of smaller Pythagorean triples. For example if we multiply (3, 4, 5) by 2, we get another triple: (6, 8, 10).
If a Pythagorean triple is not a multiple of another smaller Pythagorean triple, then it is called a primitive Pythagorean Triple. For example, (3, 4, 5) and (5, 12, 13) are primitive Pythagorean triples, however, (10, 24, 26) is not a primitive Pythagorean triple because is it 2 × (5, 12, 13).
To find primitive Pythagorean triples, substitute integer values of m and n into the formulae:
- a = m2 – n2
- b = 2mn
- c = m2 + n2
For example, if m = 2 and n = 1, the first Pythagorean triple is found:
- a = 22 – 12 = 3
- b = 2 × 2 × 1 = 4
- c = 22 + 12 = 5
The first Pythagorean triple is (3, 4, 5).
We can then find all other Pythagorean triples by multiplying these primitive Pythagorean triples by any integer number.
Properties of Primitive Pythagorean Triples
The following properties apply to primitive Pythagorean triples:
- Pythagorean triples must satisfy a2 + b2 = c2
- Exactly one number out of a, b and c must be divisible by 5
- c is always odd
- c is always one larger than a multiple of 4
- c is never divisible by 3
- Exactly one of a or b is even
- Exactly one of a or b is divisible by 3
