How to do the Binomial Expansion

Binomial Expansion Video Lessons

How to do the Binomial Expansion

Binomial Expansion – Negative Powers

What is the Binomial Theorem?

The binomial theorem is an algebraic method for expanding any binomial of the form (a+b)ⁿ without the need to expand all n brackets individually. The binomial theorem formula states that .

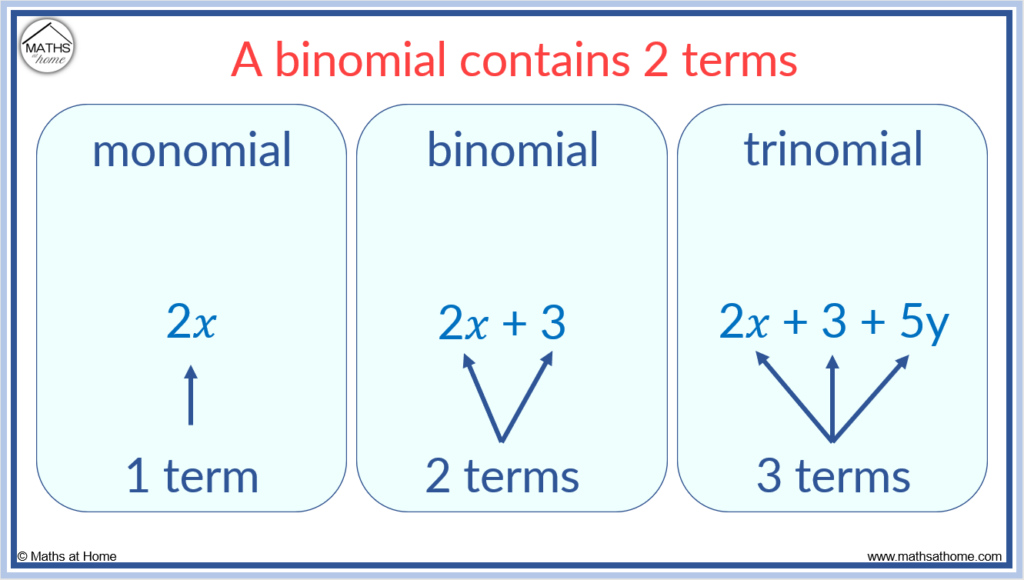
A binomial contains exactly two terms. These 2 terms must be constant terms (numbers on their own) or powers of 𝑥 (or any other variable).

A binomial can be raised to a power such as (2𝑥+3)⁵, which means (2𝑥+3)(2𝑥+3)(2𝑥+3)(2𝑥+3)(2𝑥 +3). However, expanding this many brackets is a slow process and the larger the power that the binomial is raised to, the easier it is to use the binomial theorem instead.

Here are the first 5 binomial expansions as found from the binomial theorem.

Simply substitute ‘a’ with the first term of the binomial and ‘b’ with the second term of the binomial.

For example, expand (2𝑥+3)⁵.

In this example, ‘a’ = 2𝑥 and ‘b’ = 3.

We want the expansion that contains a power of 5:

a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Substituting in the values of ‘a’ = 2𝑥 and ‘b’ = 3, we get:

(2𝑥)⁵ + 5 (2𝑥)⁴ (3) + 10 (2𝑥)³ (3)² + 10 (2𝑥)² (3)³ + 5 (2𝑥) (3)⁴ + (3)⁵

We then simplify the terms to get:

(2𝑥+3)⁵ = 32𝑥⁵ + 240𝑥⁴ + 720𝑥³ + 1080𝑥² + 810𝑥 + 243

How to do a Binomial Expansion with Pascal’s Triangle

The numbers in Pascal’s triangle form the coefficients in the binomial expansion. For any binomial expansion of (a+b)ⁿ, the coefficients for each term in the expansion are given by the nth row of Pascal’s triangle. For example, if a binomial is raised to the power of 3, then looking at the 3rd row of Pascal’s triangle, the coefficients are 1, 3, 3 and 1.

Here are the first five binomial expansions with their coefficients listed. Each binomial coefficient is found using Pascal’s triangle.

This animation also tells us the ⁿC_r calculation which can be used to work these coefficients out on a calculator.

binomial expansion coefficients from pascals triangle

To use Pascal’s triangle to do the binomial expansion of (a+b)ⁿ :

Find the number of terms and their coefficients from the nth row of Pascal’s triangle.
Start with the first term containing aⁿ and no b terms.
Reduce the power of a with each term of the expansion.
Increase the power of b with each term of the expansion.
Simplify each of the terms in the expansion.

For example, expand (𝑥 + 2)³.

Step 1. We have a binomial to the power of 3 so we look at the 3rd row of Pascal’s triangle. We have 4 terms with coefficients of 1, 3, 3 and 1.

Step 2. a is the first term inside the bracket, which is 𝑥 and b is the second term inside the bracket which is 2. n is the power on the brackets, so n = 3.

We start with the first term as aⁿ , which here is 𝑥³.

Step 3. We reduce the power of the 𝑥 with each term of the expansion. So 𝑥³ becomes 𝑥², then 𝑥 and finally it disappears entirely by the fourth term.

Step 4. We increase the power of the 2 with each term in the expansion. We start with zero 2s, then 2¹, 2² and finally we have 2³ in the fourth term.

Step 5. We now simplify each term by multiplying out the numbers to find the coefficients and then looking at the power of 𝑥 in each of the terms.

For example, the second term of 3(𝑥)²(2) becomes 6𝑥² since 3 × 2 = 6 and the 𝑥 is squared.

(𝑥 + 2)³ = 𝑥³ + 6𝑥² + 12𝑥 + 8

For example, expand (2𝑥 – 1)⁴

In this example, we must note that the second term in the binomial is -1, not 1. Therefore b = -1. It is a common mistake to forget this negative in binomials where a subtraction is taking place inside the brackets.

Step 1. We have a binomial raised to the power of 4 and so we look at the 4th row of the Pascal’s triangle to find the 5 coefficients of 1, 4, 6, 4 and 1.

Step 2. We start with (2𝑥)⁴. It is important to keep the 2𝑥 term inside brackets here as we have (2𝑥)⁴ not 2𝑥⁴.

Step 3. We reduce the power of (2𝑥) as we move to the next term in the binomial expansion. (2𝑥)⁴ becomes (2𝑥)³, (2𝑥)², (2𝑥) and then it disappears entirely by the 5th term.

Step 4. We increase the (-1) term from zero up to (-1)⁴.

Step 5. We simplify the terms. There are two areas to focus on here.

Firstly, (2𝑥)⁴ means 2⁴ multiplied by 𝑥⁴. (2𝑥)⁴ = 16𝑥⁴.

Secondly, negative numbers to an even power make a positive answer and negative numbers to an odd power make an odd answer. So (-1)⁴ = 1 because 4 is even. However, (-1)³ = -1 because 3 is odd.

(2𝑥 – 1)⁴ = 16𝑥⁴ – 32𝑥³ + 24𝑥² – 8𝑥 + 1

We can see that when the second term ‘b’ inside the brackets is negative, the resulting coefficients of the binomial expansion alternates from positive to negative. We alternate between + and – signs in between the terms of our answer.

What is the Binomial Expansion Formula?

The binomial expansion formula is . Where $the 2 by 1 column matrix n k equals the fraction with numerator n factorial and denominator k factorial open paren n minus k close paren factorial$ .

This can be more easily calculated on a calculator using the ⁿC_r function.

The ! sign is called factorial. The factorial sign tells us to start with a whole number and multiply it by all of the preceding integers until we reach 1. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120.

Using the Binomial Expansion Formula

In words, the binomial expansion formula tells us to start with the first term of a to the power of n and zero b terms. As we move from term to term, the power of a decreases and the power of b increases.

We multiply each term by the binomial coefficient which is calculated by Find the ⁿC_r feature on your calculator and n will be the power on the brackets and r will be the term number in the expansion starting from 0.

Here is an animation explaining how the ⁿC_r feature can be used to calculate the coefficients. For example, 4C₂ = 6.

The sigma summation sign tells us to add up all of the terms from the first term aⁿ until the last term bⁿ.

Here is an example of using the binomial expansion formula to work out (a+b)⁴.

Here, n = 4 because the binomial is raised to the power of 4.

Term	Coefficient calculation	Complete term in the expansion
1st term	4C₀ = 1	a⁴
2nd term	4C₁ = 4	4a³b
3rd term	4C₂ = 6	6a²b²
4th term	4C₃ = 4	4ab³
5th term	4C₄ = 1	b⁴

Therefore summing these 5 terms together, (a+b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

We start with the first term to the nth power. We decrease this power as we move from one term to the next and increase the power of the second term. The coefficients are calculated as shown in the table above.

Here is a list of the formulae for all of the binomial expansions up to the 10th power.

Binomial	Binomial Expansion Formula
(a + b)¹	= a + b
(a + b)²	= a² + 2ab + b²
(a + b)³	= a³ + 3a²b + 3ab² + b³
(a + b)⁴	= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a + b)⁵	= a⁵ + 5a⁴b +10a³b² + 10a²b³ + 5^ab⁴ + b⁵
(a + b)⁶	= a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶
(a + b)⁷	= a⁷ + 7a⁶b + 21a⁵b² + 35a⁴b³ + 35 a³b⁴ + 21a²b⁵ + 7ab⁶ + b⁷
(a + b)⁸	= a⁸ + 8a⁷b + 28a⁶b² + 56a⁵b³ + 70a⁴b⁴ + 56a³b⁵ + 28a²b⁶ + 8ab⁷ + b⁸
(a + b)⁹	= a⁹ + 9a⁸b + 36a⁷b² + 84a⁶b³ + 126a⁵b⁴ + 126a⁴b⁵ + 84a³b⁶ + 36a²b⁷ + 9ab⁸ + b⁹
(a + b)¹⁰	= a¹⁰ + 10a⁹b + 45a⁸b² + 120a⁷b³ + 210a⁶b⁴ + 252a⁵b⁵ + 210a⁴b⁶ + 120a³b⁷ + 45a²b⁸ +10ab⁹ + b¹⁰

Binomial Expansion with a Negative Power

If the power that a binomial is raised to is negative, then a Taylor series expansion is used to approximate the first few terms for small values of 𝑥. For a binomial with a negative power, it can be expanded using $open paren 1 plus x close paren to the n-th power equals 1 plus n x plus the fraction with numerator n times open paren n minus 1 close paren and denominator 2 factorial x squared plus the fraction with numerator n times open paren n minus 1 close paren times open paren n minus 2 close paren and denominator 3 factorial x cubed plus period period period$

It is important to note that when expanding a binomial with a negative power, the series expansion only works when the first term inside the brackets is 1.

To expand a binomial with a negative power:

Factorise the binomial if necessary to make the first term in the bracket equal 1.
Substitute the values of ‘n’ which is the negative power and ‘𝑥’ which is the other term in the brackets alongside the 1.
Simplify each term of the expansion.
Write the values of 𝑥 for which the expansion is valid. ‘𝑥’ must be between -1 and 1.

For example, find the binomial expansion for (2 + 10𝑥)^-2

Here we have a negative power. n = -2.

Step 1. The first term inside the brackets must be 1. Ours is 2. We must factor out the 2.

The factor of 2 comes out so that inside the brackets we have 1+5𝑥 instead of 2+10𝑥.

We can see that the 2 is still raised to the power of -2. Therefore .

It is important to remember that this factor is always raised to the negative power as well.

This factor of one quarter must move to the front of the expansion. The rest of the expansion can be completed inside the brackets that follow the quarter.

The (1+5𝑥)^-2 is now ready to be used with the series expansion for (1 + 𝑥)ⁿ formula because the first term is now a 1.

Step 2. We substitute in the values of ‘n’ = -2 and ‘𝑥’ = 5𝑥 into the series expansion.

Step 3. We now simplify each term.

Once each term inside the brackets is simplified, we also need to multiply each term by one quarter.

Step 4. The expansion is valid for -1 < ‘𝑥’ < 1. Our ‘𝑥’ is 5𝑥 and so we have -1 < 5𝑥 < 1. Dividing each term by 5, we see that the expansion is valid for

Binomial Expansion with a Fractional Power

The binomial theorem can be applied to binomials with fractional powers. The series expansion $open paren 1 plus x close paren to the n-th power equals 1 plus n x plus the fraction with numerator n times open paren n minus 1 close paren and denominator 2 factorial x squared plus the fraction with numerator n times open paren n minus 1 close paren times open paren n minus 2 close paren and denominator 3 factorial x cubed plus period period period$ can be used to find the first few terms of the expansion. n is the value of the fractional power and 𝑥 is the term that accompanies the 1 inside the binomial.

For example, find the first 4 terms of

First write this binomial so that it has a fractional power. The square root around 1+ 5𝑥 is replaced with the power of one half.

Therefore ‘𝑥’ = 5𝑥 and ‘n’ = .

We substitute the values of n and 𝑥 into the series expansion formula as shown.

We then simplify each term.

When using this series to expand a binomial with a fractional power, the series is valid for -1 < 𝑥 < 1. In this example, the 𝑥 value is 5𝑥.

Therefore the series is valid for -1 < 5𝑥 < 1. Dividing each term by 5, we get

Binomial Expansion with Two Brackets

To expand two brackets where one the brackets is raised to a large power, expand the bracket with a large power separately using the binomial expansion and then multiply each term by the terms in the other bracket afterwards.

For example, expand the two brackets (1+𝑥)(2𝑥+3)⁴ with binomial expansion

In this example, we have two brackets: (1 + 𝑥) and (2𝑥 + 3)⁴ .

We first expand the bracket with a higher power using the binomial expansion.

(2𝑥 + 3)⁴ = 16𝑥⁴ + 96𝑥³ + 216𝑥² + 216𝑥 + 81

This expansion is equivalent to (2𝑥 + 3)⁴. We want to find (1 + 𝑥)(2𝑥 + 3)⁴.

We must multiply all of the terms by (1 + 𝑥). We multiply the terms by 1 and then by 𝑥 before adding them together.

The result is 16𝑥⁵ + 112𝑥⁴ + 312𝑥³ + 432𝑥² + 297𝑥 + 81

Binomial Expansion Video Lessons