Video Lesson: What are the Double Angle Formulas?
Video Lesson: How to Use the Double Angle Formulas
What are the Double Angle Formulae?
The double angle formulae are:
- sin(2θ)=2sin(θ)cos(θ)
- cos(2θ)=cos2θ-sin2θ
- tan(2θ)=2tanθ/(1-tan2θ)
The double angle formulae are used to simplify and rewrite expressions, allowing more complex equations to be solved. They are also used to find exact trigonometric values for multiples of a known angle.
Double Angle Formulae List
Here is a list of the double angle formulae.

- The double angle formula for sine is
.
- The double angle formula for cosine is
. This can also be written as
or
.
- The double angle formula for tangent is
.
Double Angle Formula Derivation
To derive the double angle formulas, start with the compound angle formulas, set both angles to the same value and simplify. The best way to remember the double angle formulas is to derive them from the compound angle formulas.
Double Angle Formula for Sine
To derive the sine double angle formula,
- Start with the compound angle formula
- Substitute B=A to obtain
- This simplifies to

Double Angle Formula for Cosine
To derive the cosine double angle formula,
- Start with the cosine compound angle formula,
- Substitute B=A to obtain
- Simplify to obtain

The cosine double angle formula can be rewritten in two different forms using the Pythagorean identity .
can be rearranged as either:
To rearrange the double angle formula for cosine, substitute into
This becomes .
Simplifying, this becomes .
Alternatively, the double angle formula for cosine can be rearranged by substituting into
.
This becomes .
Simplifying, this becomes .

The double angle formula for cosine is written in the following three ways:
Double Angle Formula for Tangent
To derive the tangent double angle formula,
- Start with the tangent compound angle formula,
- Substitute B=A to obtain
- Simplify to obtain

Rewriting Expressions Using the Double Angle Formulae
To simplify expressions using the double angle formulae, substitute the double angle formulae for their single-angle equivalents. The tanx=sinx/cosx and the Pythagorean trigonometric identity of sin2x+cos2x=1 may also be needed.
Example 1
Show that .
We start by substituting the two double angle formulae for sine and cosine.
or
or
We will choose to substitute the equation because subtracting the1 will cancel out the 1 already on the denominator.
becomes
.
This simplifies to . We can now divide the numerator and denominator both by
to obtain
which equals
.
Example 2
Show that .
We start with the left hand side of the equation, substituting the double angle formula of .
The equation becomes .
Looking at the fraction, there is nothing we can divide each term by. Instead we can multiply both sides of the fraction by the denominator of .
becomes
.
Expanding the brackets on the right hand side of the equation, .
This simplifies so that the left hand side equals the right hand side: .
Example 3
Show that .
We avoid the temptation to replace as
does not feature on the left hand side of the equation. Instead, we will use the double angle formula.
We will substitute so that
.
We can simplify this fraction by dividing the numerator and denominator by 2 to obtain .
So far, the equation becomes .
We will add the fractions on the right hand side of the equation so that they become one fraction.
Using the Pythagorean trigonometric identity, , we obtain
.
Finding Exact Values Using the Double Angle Formulae
Example 1
If find the exact value of
.
Since , simply substitute
into this equation.
Evaluating this, we obtain .
The answer is left as a fraction to leave it in exact form.

Example 2
When calculating exact trigonometric values, it is important to know which quadrant the angle given is in.
Angles between are in quadrant 1
Angles between are in quadrant 2
Angles between are in quadrant 3
Angles between are in quadrant 4
If , find the exact value of
, where
.
Since the angle is between , we draw a triangle in the first quadrant.
Since and
, then the opposite side must be 3 and the adjacent side must be 4.
We label those sides on the triangle.
We then use Pythagoras’ theorem to find the hypotenuse.
Now that we know all three sides of the triangle, we can find and
.
and
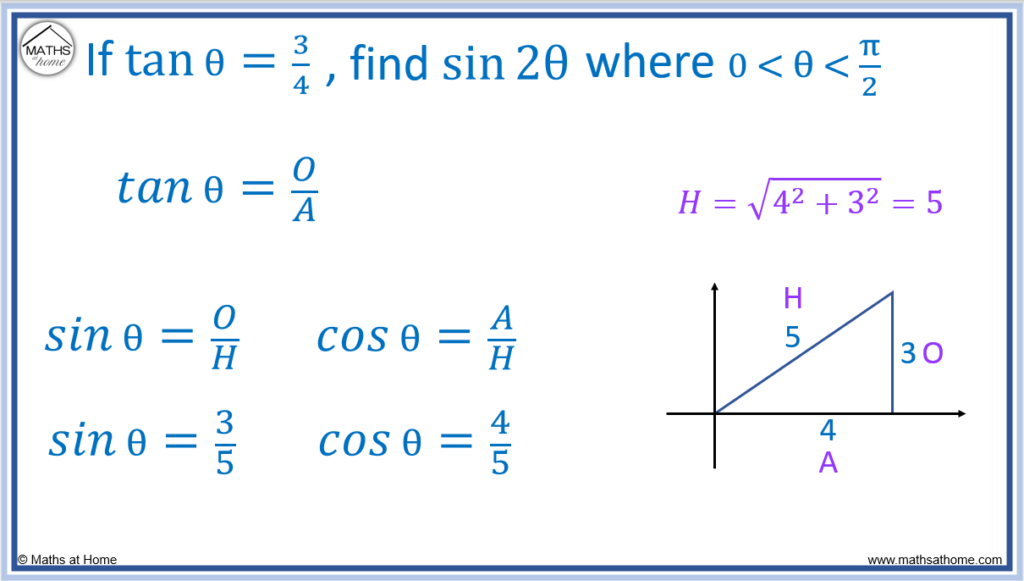
Now can be found using the double angle formula
.
Since and
, the double angle formula becomes
.
Evaluating this, .

Example 3
If , find
where
.
With , the angle is in quadrant 4. The triangle is drawn below.
Since and
, the adjacent = 12 and the hypotenuse = 13.
Using Pythagoras theorem, . Since the opposite side is below the x-axis, the opposite side length is -5.
Now that all sides of the triangle are known, .

.
Using the double angle formula, ,
.
Substituting and
, this becomes
.
This can be evaluated as
Triple Angle Formulae
The triple angle formulae are:
- sin(3θ)=3sinθ-4sin3θ
- cos(3θ)=4cos3θ-3cosθ
- tan(3θ)=(3tanθ-tan3θ)/(1-3tan2θ)

Sine Triple Angle Formula
To derive the sine triple angle formula, the addition angle formula for sine is used: .
Here, the values of and
are used so that
.
Then the double angle formula are used : and
.
Therefore becomes
.
This simplifies to .
We can now substitute to obtain
.
Expanding, this becomes .
Collecting like terms, this becomes .
Cosine Triple Angle Formula
To derive the cosine triple angle formula, the addition formula for cosine is used:
Here, the values of and
are used so that
.
We now substitute the sine and cosine double angle formulae: and
.
Therefore we obtain .
Expanding, we obtain .
We now substitute to obtain
.
Expanding the brackets, we obtain .
Collecting like terms, we obtain .
