Video Lesson: How to Do Differentiation from First Principles
What is Differentiation by First Principles?
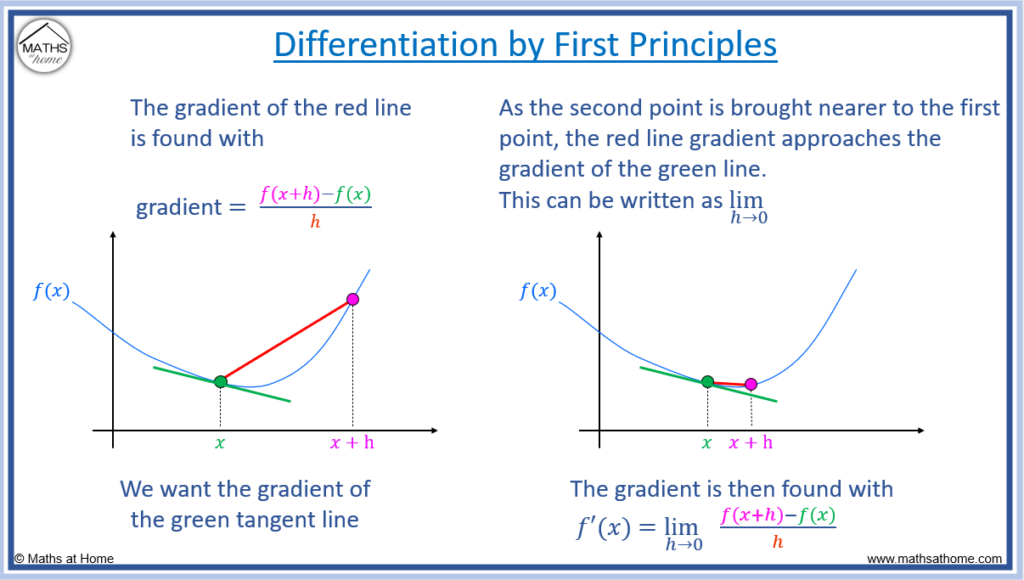
Differentiation by first principles is an algebraic technique for calculating the gradient function. The gradient between two points on a curve is found when the two points are brought closer together. The gradient is given by the equation f'(x)=limh→0[f(x+h)-(fx)]/h.
Derivation of Differentiation by First Principles Equation
Differentiation by first principles is used to find the gradient of a tangent at a point. The method involves finding the gradient between two points. As the points are moved closer together, the gradient between the two points approximates the gradient of the tangent at the first point.
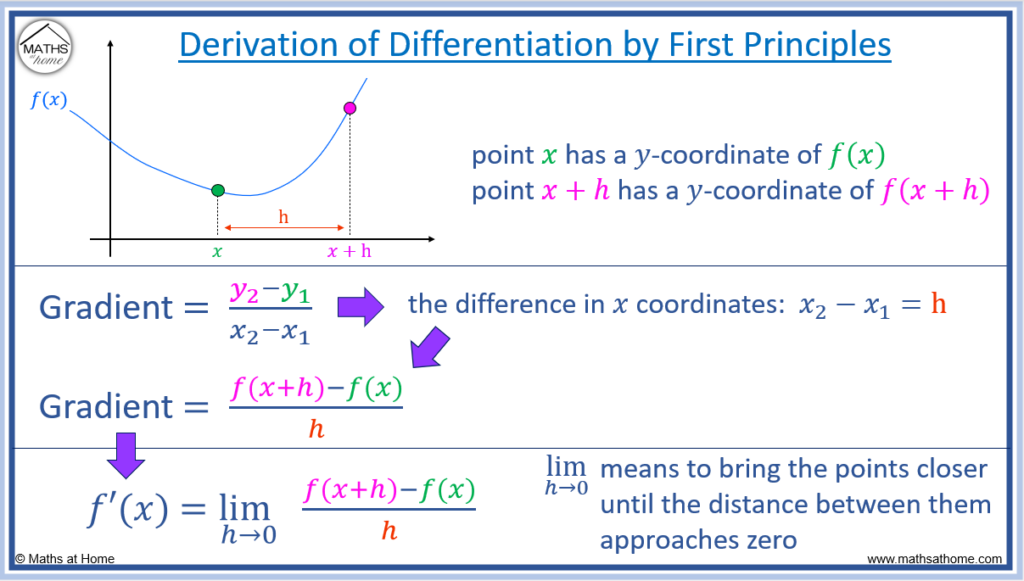
The process involves considering the gradient between any two points on a curve. The gradient between two points can be written as follows:
, where the two points have the coordinates
and
.
We will consider two points with a horizontal distance between them of ‘h’.
These points will have 𝑥-coordinates of 𝑥 and 𝑥+h.
Therefore these two points will have y-coordinates of and
respectively, since they will lie on the curve
.
The two points have coordinates and
.
Therefore ,
,
and
.
Therefore, since , the gradient between the two points can be written as:
.
This simplifies to .
This equation tells us the gradient between the two points as shown by the red line in the image above.
Since we wish to find the gradient of the tangent to the curve at the location of the first point, the second point is brought closer to the first point.
This is shown in the image above. We can see in the second graph, the red gradient line is a better approximation to the green tangent gradient as the points are closer together.
The gradient between the two points (red line) will equal the gradient of the tangent at the first point (green line) when the distance between the two points approaches zero.
Mathematically, this is equivalent to the distance between the points ‘h’, tending to zero.
We write this as . This means that we are reducing the value of ‘h’ so that it tends to a value of zero.
We add this limit to our gradient equation and write the gradient in function notation as to obtain the first principles equation.
becomes
.
Differentiation by First Principles Formula
The differentiation by first principles formula is f'(x)=limh→0[f(x+h)-(fx)]/h. For any function f(x), find f(x+h) by replacing x with x+h and substitute f(x+h) and f(x) into the formula. Simplify the numerator and divide all terms by h. Finally evaluate the limh→0 by substituting h = 0. The result is the gradient function of f(x).

The formula for differentiation by first principles
In the formula for differentiation by first principles:
- f(𝑥) is the function
- f(𝑥+h) is found by substituting 𝑥 with 𝑥+h in f(𝑥)
- h is the distance between the two points
How to Do Differentiation by First Principles
To do differentiation by first principles:
- Find f(x+h) by substituting x with x+h in the f(x) equation.
- Substitute f(x+h) and f(x) into the first principles equation.
- Simplify the numerator.
- Divide all terms by h.
- Substituting h=0 to evaluate the limit.
Example: Differentiate f(𝑥) = 2𝑥 + 5 using first principles
We already know that .
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
becomes
when
is replaced with
.
Therefore .
Expanding the bracket, .

Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation is .
and .
Substituting these in, we obtain: .

Step 3. Simplify the numerator
Expanding the brackets on the top of the numerator, becomes
.
Notice that the negative sign in front of the (2x+5) results in -2𝑥 and -5.

Then the cancels with
and +5 cancels with -5.
We are left with .
Step 4. Divide all terms by h
Within there is an h term on the numerator and denominator.
Dividing both the numerator and denominator by h, the equation simplifies to .

Step 5. Substitute h=0 to evaluate the limit
To evaluate the limit in , simply substitute h=0 into any h terms after the limit.
After the limit we simply have a 2. There are no h terms in this example.
Therefore nothing changes for us in this step this time.
.
Therefore .

This means that the gradient at all points along is always equal to 2.
Differentiation by First Principles of a Quadratic
Differentiate using first principles.
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
Every 𝑥 term is replaced with 𝑥+h. Substitute the whole of 𝑥+h in brackets.
becomes
.
Expanding
and so, .
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
and
.
becomes
.

Step 3. Simplify the numerator
Expanding, .
Therefore becomes
.
Now the cancels with
and
cancels with
.
The equation becomes .

Step 4. Divide all terms by h
All h terms on the numerator and on the denominator must be divided by h.
becomes
.
Step 5. Substitute h=0 to evaluate the limit
To evaluate the limit, substitute h=0.
becomes
.

Differentiation by First Principles of a Cubic
Differentiate f(𝑥)=2𝑥3 by first principles.
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
.
To find , substitute
with
to get
.

Now via the binomial expansion .
Therefore .
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
becomes
.
Step 3. Simplify the numerator
The 2𝑥3 cancels with the -2𝑥3 on the numerator.
becomes
.

Step 4. Divide all terms by h
Dividing all terms by h, becomes
.
Step 5. Substitute h=0 to evaluate the limit
Finally, substituting all h terms with h=0, becomes
.

Therefore the gradient function of is
.
Differentiation by First Principles with Rational Functions
To differentiate a function of 𝑥 with a negative power using the first principles method, write the function as a fraction with a positive power. For example, 𝑥-1 can be written as 1/𝑥.
Differentiate using first principles.
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
If then
.
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation of becomes
.

Step 3. Simplify the numerator
The numerator of the fraction contains the subtraction of two fractions.
can be written as one fraction with a common denominator of
. Simply multiply the numerator and denominator of
by
and multiply the numerator and denominator of
by
.
The fraction subtraction can be written as , which can be written as one fraction as
.
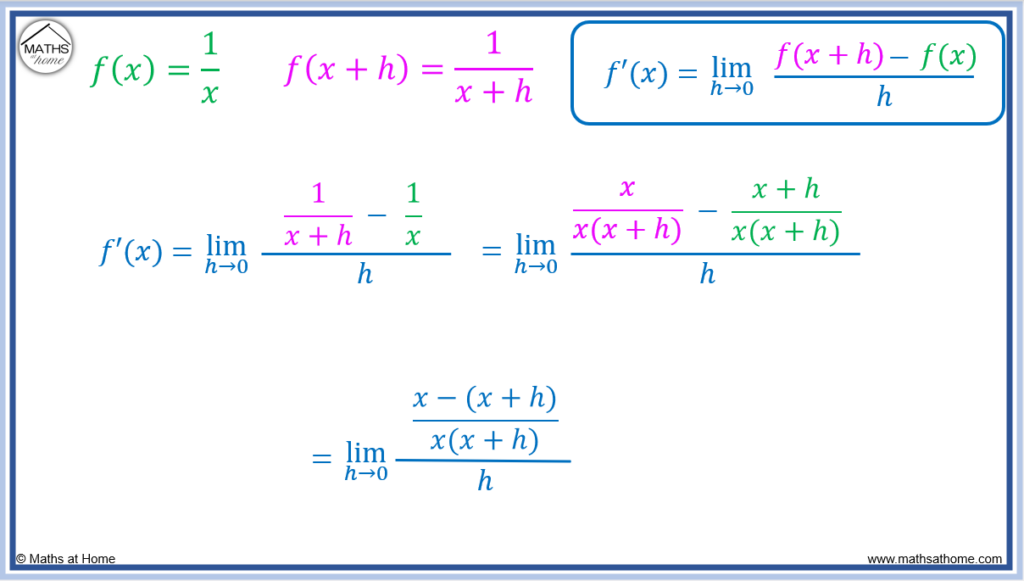
To differentiate a fraction using first principles, combine the fractions formed by into one fraction. This fraction is then within the numerator of the overall fraction in the first principles equation.
To simplify this further, multiply the numerator and denominator of the overall fraction by the denominator of the fraction on the numerator of the overall fraction.
In this example, can be simplified by multiplying by
.
and so,
.
Finally, the numerator can simplify further to .

Step 4. Divide all terms by h
The numerator and denominator of both contain an h term.
Dividing both the numerator and denominator by h, we obtain .

Step 5. Substitute h=0 to evaluate the limit
Finally, to evaluate the limit of , substitute h=0 to obtain
.
Simplified, the derivative is .

Differentiate by First Principles of the Square Root of 𝑥
To differentiate a square root function using first principles, multiply the numerator and denominator of the fraction formed by the conjugate of the numerator. This simplifies the equation by removing the square root.
Differentiate .
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
If then
.
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation of becomes
.
Step 3. Simplify the numerator
To simplify the numerator, we multiply the numerator and denominator by the conjugate of the numerator. That is, the negative sign in the numerator replaced with an addition sign. The conjugate of is
.
Multiplying . This then simplifies to h.
The full working out for this can be seen as follows.
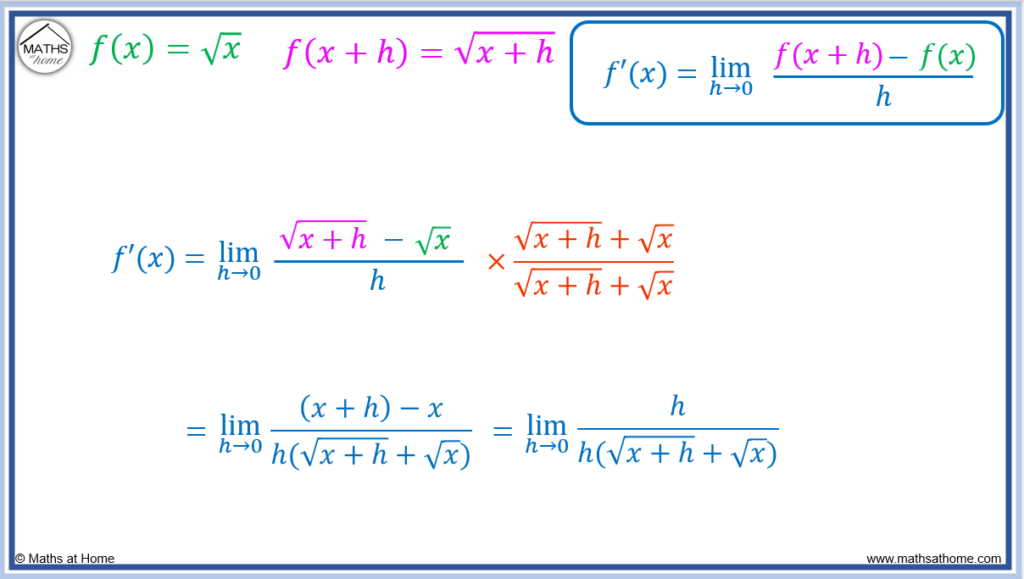
Therefore, .
Step 4. Divide all terms by h
In , there is an h term in both the numerator and denominator of the fraction,
Dividing by h, this becomes .
Step 5. Substitute h=0 to evaluate the limit
To evaluate the limit of , substitute h=0 to obtain
.
This simplifies to .
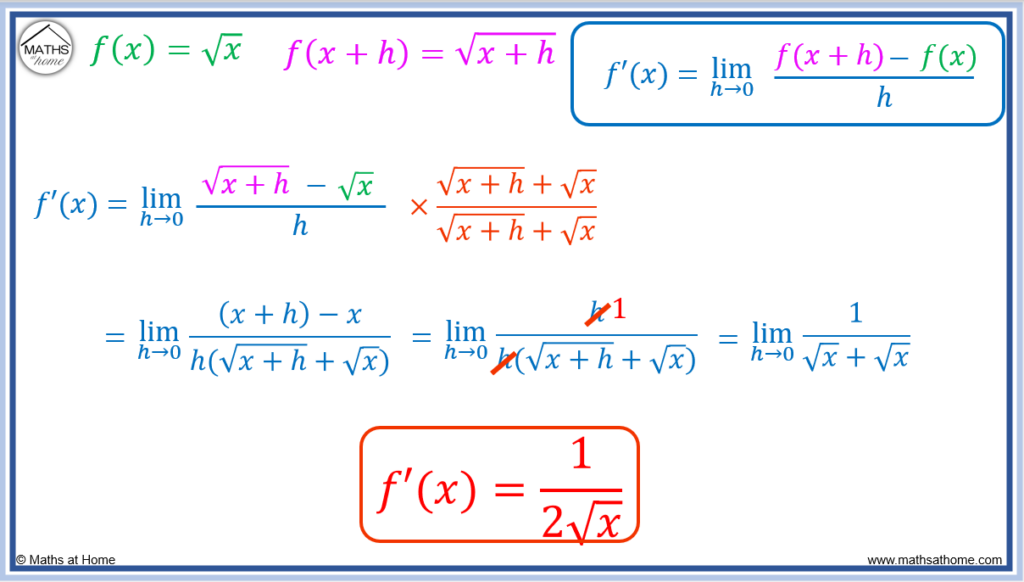
Differentiate by First Principles: f(x) = 1/√x
To differentiate a function with both a fraction and a square root using first principles, a combination of the techniques for differentiating fractions and square roots must be used. That is, combine the two fractions into one fraction first and then multiply through by the conjugate.
Differentiate using first principles.
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
Since then
.
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation of becomes
.
Step 3. Simplify the numerator
The two fractions can be combined into one by finding a common denominator of .
The derivative becomes which can be written as
.

To simplify further, multiply by
to obtain
.
Square roots must be removed on the numerator by multiplying by the conjugate.
The conjugate of is
.
.
This simplifies the derivative to .

Step 4. Divide all terms by h
contains an h term on the numerator and denominator.
This simplifies to .
Step 5. Substitute h=0 to evaluate the limit
Substituting h=0, the limit of becomes
.
This simplifies to , which can be written as
.

Differentiate by First Principles: sin(x)
Differentiating the sine function using first principles involves the compound angle formula for sine and the small angle approximations.
Differentiate .
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
Since ,
.
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation of becomes
.
Step 3. Simplify the numerator
To simplify the numerator, the compound angle formula for sine must be used.
Since , we can write
.
The first principles formula becomes .
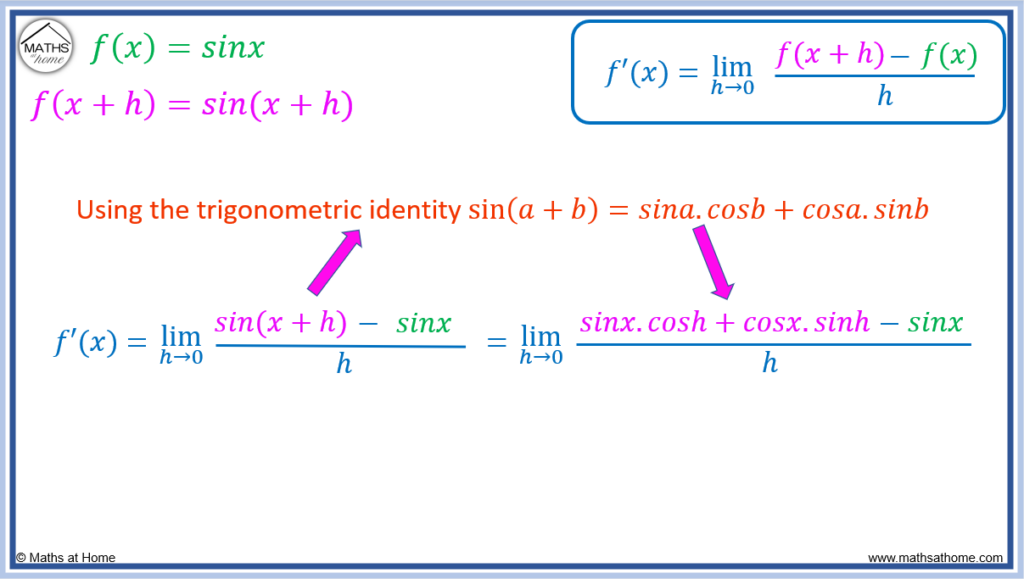
To simplify the numerator further, the small angle approximations must be used.
As , the value of h tends to zero.
The small angle approximations tell us that .
Therefore we can replace sin(h) with h and cos(h) with 1.
becomes
.
This simplifies to .
This simplifies further to

Step 4. Divide all terms by h
Now simplifies to
.
Step 5. Substitute h=0 to evaluate the limit
There are no h terms remaining in and so, substituting h=0, this becomes
.

Differentiate by First Principles: cos(x)
Differentiate from first principles.
Step 1. Find f(𝑥+h) by substituting 𝑥 with 𝑥+h in the f(𝑥) equation
Since ,
.
Step 2. Substitute f(𝑥+h) and f(𝑥) into the first principles equation
The first principles equation of becomes
.
Step 3. Simplify the numerator
To simplify the numerator, the compound angle formula for cosine must be used.
Since , we can write
.
The first principles formula becomes .
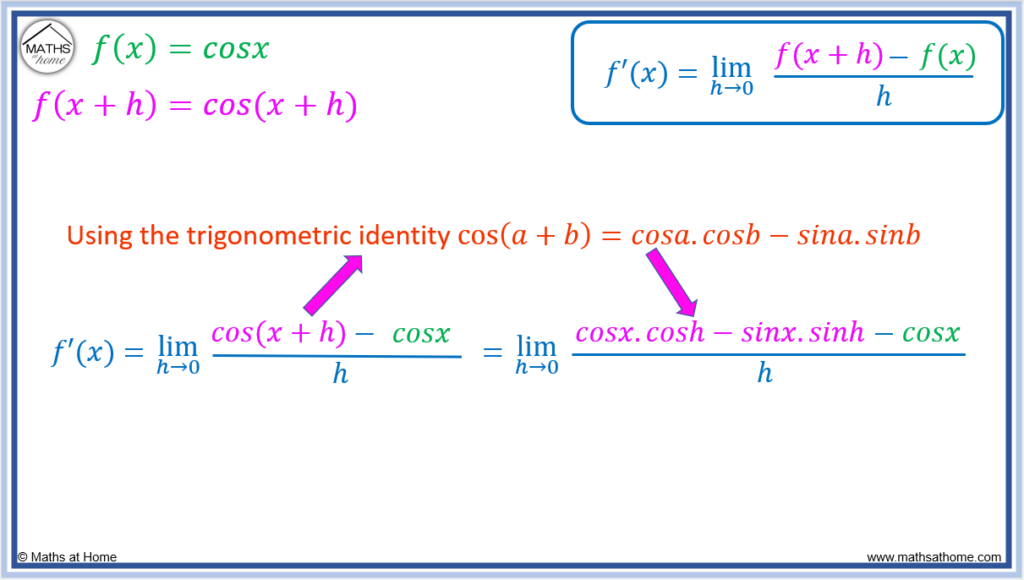
To simplify the numerator further, the small angle approximations must be used.
As , the value of h tends to zero.
The small angle approximations tell us that .
Therefore we can replace sin(h) with h and cos(h) with 1.
becomes
which simplifies to
.
The cosx and -cosx terms cancel so this simplifies further to .

Step 4. Divide all terms by h
Now simplifies to
.
Step 5. Substitute h=0 to evaluate the limit
There are no h terms remaining in and so, substituting h=0, this becomes
.

Differentiate by First Principles: ln(x)
Differentiating ln(x) from first principles requires the use of log laws to simplify the equation to one log. Then the limit definition of ex is used to simplify the equation to 1/x.
Differentiate .
Since ,
.
The first principles equation of becomes
.
This can be written as .
Using log laws, .
Simplifying the fraction inside the natural logarithm, this becomes .

To simplify this further, the limit definition for Euler’s number is used.
Euler’s number e is defined as .
Therefore .
Making the substitution of and by rearrangement of this,
, we obtain
.
Now replacing with
, we can see that
.
We had previously seen that from first principles, .
Using log laws, this can be written as .
This can be written as by bringing the logarithm in front of the limit.
Now using the definition of , the derivative becomes
.
Finally, since the natural logarithm and the exponential are inverse functions, we obtain .

Differentiate by First Principles: ex
To differentiate ex using first principles, a limit definition of limh→0[eh-1]/h = 1 is used.
Differentiate .
Since ,
.
The first principles equation of becomes
.
This can be written as or
.
Since, it involves no h terms, we can bring ex outside of the limit to write this as .
To simplify this further, a limit definition of is used.
Therefore or simply
.

The derivative of is
.
