Sum to Infinity of a Geometric Series: Video Lesson
What is the Sum to Infinity?
The sum to infinity is the result of adding all of the terms in an infinite geometric series together. It is only possible to calculate the sum to infinity for geometric series that converge. This means that the size of each new term must be smaller than its previous term.
A geometric series is obtained when each term is multiplied by the same number from one term to the next. The value that each term is multiplied by to get to the next term is called the ratio.
For example, in the sequence 4+2+1+0.5+…, the terms are halving each time. Therefore .


means the sum of the first ‘n’ terms.
For example, and
.
As more terms are added, we see that ,
,
and
.
Because the terms are getting smaller and smaller, as we add more terms, we are adding an increasingly negligible amount.
Progressing further, ,
. We can see that the sum is approaching 8.
Even adding the first 20 terms, .
Eventually, if an infinite number of terms could be added, the sum would indeed approach 8.
We say that the sum to infinity is 8, or
The sum to infinity of the series is calculated by , where
is the first term and r is the ratio between each term.
For this series, where and
,
which becomes
.
The sum of an infinite number of terms of this series is 8.
This means that the sequence sum will approach a value of 8 but never quite get there.
How to Find the Sum to Infinity of a Geometric Series
The sum to infinity of a geometric series is given by the formula S∞=a1/(1-r), where a1 is the first term in the series and r is found by dividing any term by the term immediately before it.
- a1 is the first term in the series
- ‘r’ is the common ratio between each term in the series

The sum to infinity of a geometric series
To find the sum to infinity of a geometric series:
- Calculate r by dividing any term by the previous term.
- Find the first term, a1.
- Calculate the sum to infinity with S∞ = a1 ÷ (1-r).
For example, find the sum to infinity of the series
Step 1. Calculate r by dividing any term by the previous term
We can divide the term by the term before it, which is 1.
and so,
.
It does not matter which term you choose, simply divide any term by the term before it to find the value of r.
For example, the same result is obtained by considering the last two terms instead: .
Step 2. Find the first term, a1
The first term is simply the first number in the series, which is 1.
Step 3. Calculate the sum to infinity with S∞ = a1 ÷ (1-r)
The sum to infinity is given by .
and
.
Therefore the sum to infinity becomes which becomes
. This simplifies to
or
.

When Does the Sum to Infinity Exist?
The sum to infinity only exists if -1<r<1. If the common ratio is outside of this range, then the series will diverge and the sum to infinity will not exist. If |r|<1, the sequence will converge to the sum to infinity given by S∞=a/(1-r).
A convergent geometric series is one in which the terms get smaller and smaller. This means that the terms being added to the total sum get increasingly small. The series converges to a final value.
For example, in the series , the fractions can be seen to fit inside the area of a 1 by 1 square. Therefore the fractions
will fill an area of
.
The series converges to 1.
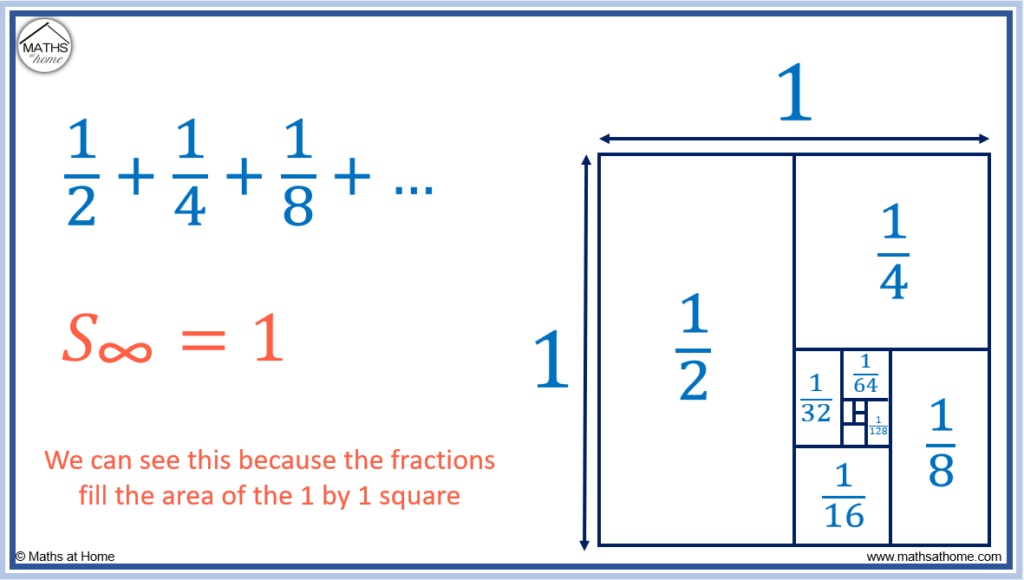
The series converges because the terms are getting smaller in magnitude. We are adding less and less each time.
Geometric series converge and have a sum to infinity if |r|<1. The common ratio must be between -1 and 1.
A geometric series diverges and does not have a sum to infinity if |r|≥1. If the terms get larger as the series progresses, the series diverges.
The sum to infinity does not exist if |r|≥1.
For example, the series is a divergent series because the terms get larger. The common ratio is 2 and a geometric series will diverge if |r|≥1.
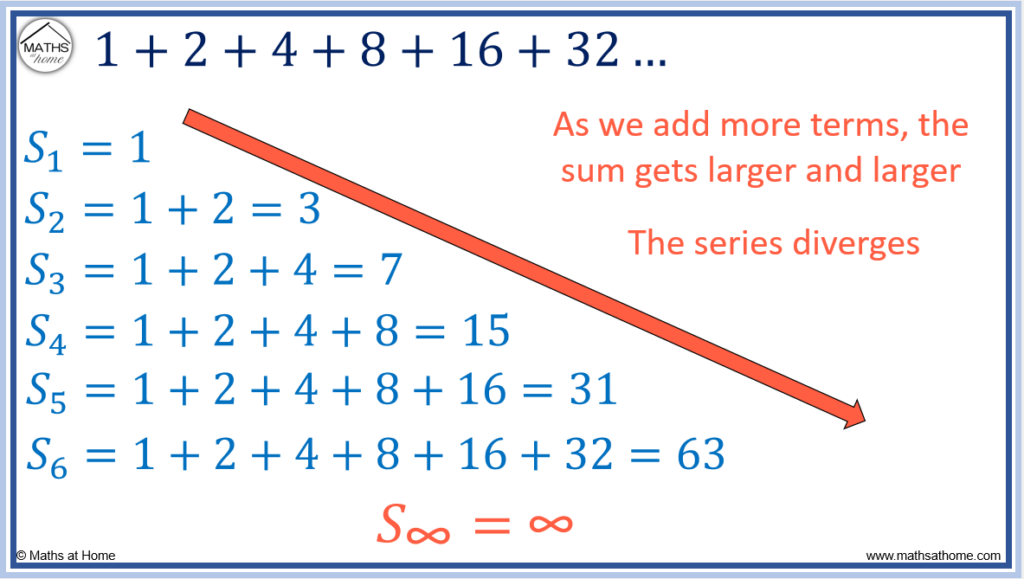
For a series to converge, the terms must get smaller and smaller in magnitude as the series progresses.
For a geometric series, the series converges if |r|<1.
Arithmetic series do not converge and so they do not have a defined sum to infinity. If the common difference is positive, then the sum to infinity of an arithmetic series is +∞. If the common difference is negative, the sum to infinity is -∞.
Sum to Infinity Calculator
Enter the first two terms of a geometric sequence into the calculator below to calculate its sum to infinity.
Negative Sum to Infinity
The sum to infinity of a geometric series will be negative if the first term of the series is negative.
This is because the sum to infinity is given by .
For a sum to infinity to exist, . This means that the denominator of the sum to infinity equation can never be negative.
The only way to obtain a negative sum to infinity is for the numerator, a1, to be negative.
a1 is the first term of the series. Hence, if the first term is negative, the sum to infinity will also be negative.
For example, find the sum to infinity of
Here, and
.
Therefore the sum to infinity becomes
which equates to
.
Sum to Infinity of an Alternating Series
A geometric series will alternate between positive and negative terms if the ratio is negative.
For example, in the series the terms alternate from negative to positive.
The ratio, .
Since , the sum to infinity
becomes
.
The denominator simplifies to and this can be evaluated so that
.
Examples of Calculating the Sum to Infinity
Here are sum examples of calculating the sum to infinity for geometric series.
In each case, the sum to infinity formula will be used, where a1 is the first term and r is the ratio.
| Geometric Series | First Term, a1 | Ratio, r | Calculation | Sum to Infinity |
| 9 | ||||
| 5 | ||||
| 9 | ||||
| 20+2+0.2+… | 20 | |||
| 4.8+1.2+0.3 | 4.8 | |||
| 4 | ||||
| -8 |
How to Write a Recurring Decimal as a Fraction with an Infinite Series
Recurring decimals can be written as a fraction using the geometric infinite series formula S∞=a/[1-r]. A decimal can be written as fractions out of 10, 100, 1000 and so on. Written in this way, the recurring decimal can be written as a geometric series in which the first term and ratio can be found.
Recurring Decimal to Fraction: Example 1
For example, write as a fraction.
The recurring decimal can be written as a series of fractions out of 10, 100, 1000 and so on.
The first term, .
The ratio is since
is divided by 10 to make
and so on.
Therefore the sum to infinity becomes
.
This simplifies so that . Evaluating
, the sum to infinity is
.
Recurring Decimal to Fraction: Example 2
Write the recurring decimal as a fraction.
Here
This can be written as
Therefore and
.
The sum to infinity becomes
.
This simplifies to and
is found to be
.
Sum to Infinity Proof
The proof of the sum to infinity formula is derived from the formula for the first n terms of a geometric series: Sn=a[1-rn]/[1-r]. If -1<r<1 then as n→∞, rn→0. Substituting rn with 0, the sum to infinity S∞=a[1-0]/[1-r], which simplifies to S∞=a/[1-r].
Here is the derivation of the sum to infinity of a geometric series in steps.
- The formula for the sum of the first n terms of a geometric series is
.
- Since
, as
,
.
- Substituting
and
into
becomes
.
- Simplifying,
.

This derivation works since the common ratio is defined to be between -1 and 1.
When a number between -1 and 1 is raised to a high power, its size decreases.
For example:
As the power tends to an infinitely large value, the decimal size tends toward zero.
As such as ,
.
This is why the ratio must be defined as -1<r<1 for a geometric series to have a sum to infinity.
