How to Change the Base of a Logarithm

How to Change the Base of a Log: Video Lesson

How to Change the Base of a Log

To change the base of a logarithm from base ‘a’ to base ‘c’, use the change of base formula: loga(b)=[logc(b)]/[logc(a)]. For example, log3(81) written in base 5 is log5(81)/log5(3).

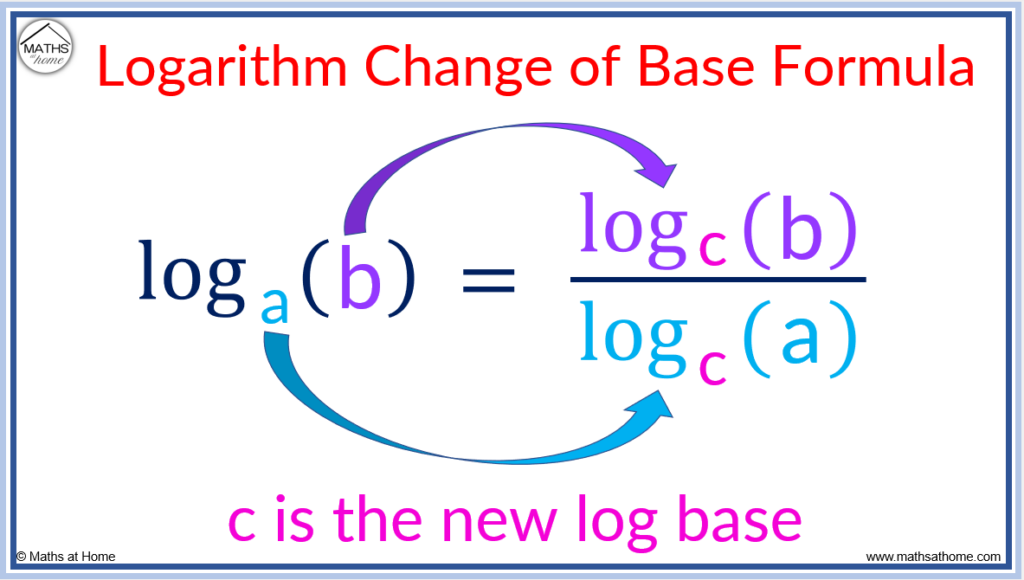
the logarithm change of base formula

The change of base rule converts a logarithm in a given base to a logarithm in a new base. The result will be a quotient (fraction) with the new logarithm as both the numerator and denominator.

the log base a. of b equals the log base c of b over the log base c of a.

The change of base rule for logarithms

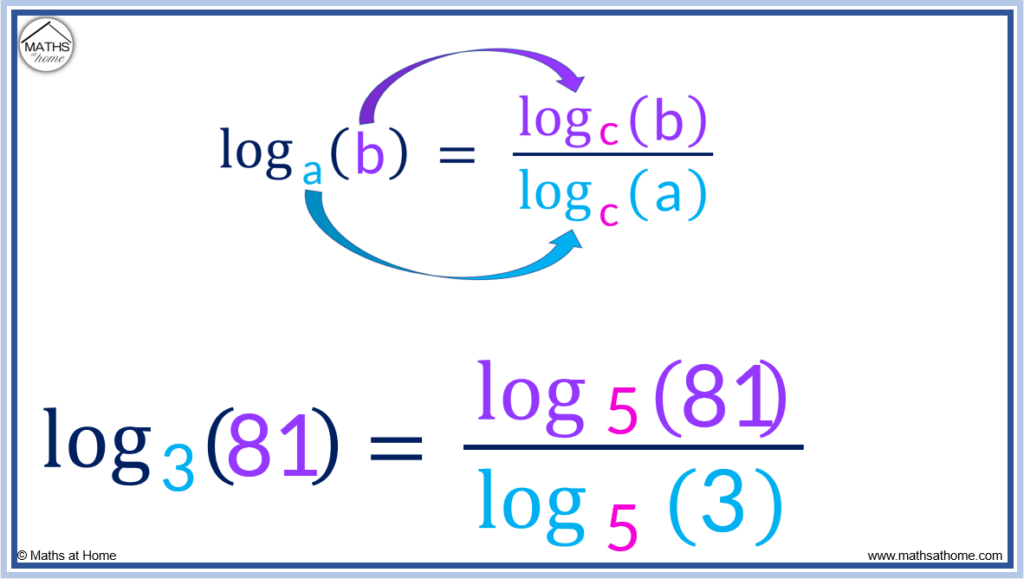
For example, convert the log base 3 of 81 to logarithm base 5.

Using the change of base formula, the log base a. of b equals the log base c of b over the log base c of a., a=3, b=81 and the new base c=5.

The base is changed to base 5 like so: the log base 3 of 81 equals the log base 5 of 81 over the log base 5 of 3.

example of using the change of base rule for logarithms

As long as the new base of the logarithm chosen is the same on the numerator and denominator of the fraction, any base can be chosen.

For example, the log base 3 of 81 can also be written in base 10 in the same manner using the log base 3 of 81 equals the log base 10 of 81 over the log base 10 of 3.

how to change the base of a logarithm

Both the log base 10 of 81 over the log base 10 of 3 and the log base 5 of 81 over the log base 5 of 3 are equal to the log base 3 of 81.

When to Use the Change of Base Formula

The change of base formula is used to rewrite a logarithm so that the logarithm has a new base. This is useful for evaluating logarithms on a calculator when only log base 10 is available. It can also be useful for simplifying some logarithmic expressions.

Some calculators do not have the function for entering different bases and simply have a ‘log’ button. This means that these calculators can only work in base 10.

For example, we previously considered the log base 3 of 81. If a calculator does not have a function for entering log base 3, then this cannot be calculated.

If the calculator has the ‘log’ button, then the base can be changed to base 10 and then evaluated. The ‘log’ button means log base 10.

change of base rule on a calculator

Here log 81 over log 3 equals 4.

Evaluating Logarithms Using the Change of Base Formula

To evaluate a logarithm using the change of base formula, use loga(b)=log(b)÷log(a). The calculation of log(b)÷log(a) can be done on a calculator to work out loga(b).

how to evaluate logs using the change of base formula

The change of base formula is the log base a. of b equals the log base c of b over the log base c of a..

By choosing the new base to be 10 and writing the fraction as a division, the change of base formula can be more easily evaluated with the following rule:

the log base a. of b equals log b divided by log a.

Change of base formula for evaluating logs

For example, evaluate the log base 3 of 10.

Here a=3 and b=10.

Using the log base a. of b equals log b divided by log a. with these values, the log base 3 of 10 equals log 10 divided by log 3.

Evaluating this on a calculator, the log base 3 of 10 almost equals 2.10

example of evaluating a logarithm using the change of base formula

Here is another example of evaluating a logarithm using the change of base formula.

Evaluate the log base 9 of 5.

Here a=9 and b=5.

Using the log base a. of b equals log b divided by log a. with these values, the log base 9 of 5 equals log 5 divided by log 9.

On a calculator, the log base 9 of 5 almost equals 0.732.

example of calculating a logarithm with a different base

Change of Base Formula with Natural Log

The change of base formula also works with the natural logarithm, ln. To change the base of a logarithm to a natural logarithm, use the formula: loga(b)=ln(b)/ln(a).

change of base to natural logarithms ln

For example, the log base 2 of 9 equals l n of 9 over l n of 2.

Natural logarithms can be evaluated on a calculator. Therefore the log base 2 of 9 equals l n of 9 over l n of 2 almost equals 3.17.

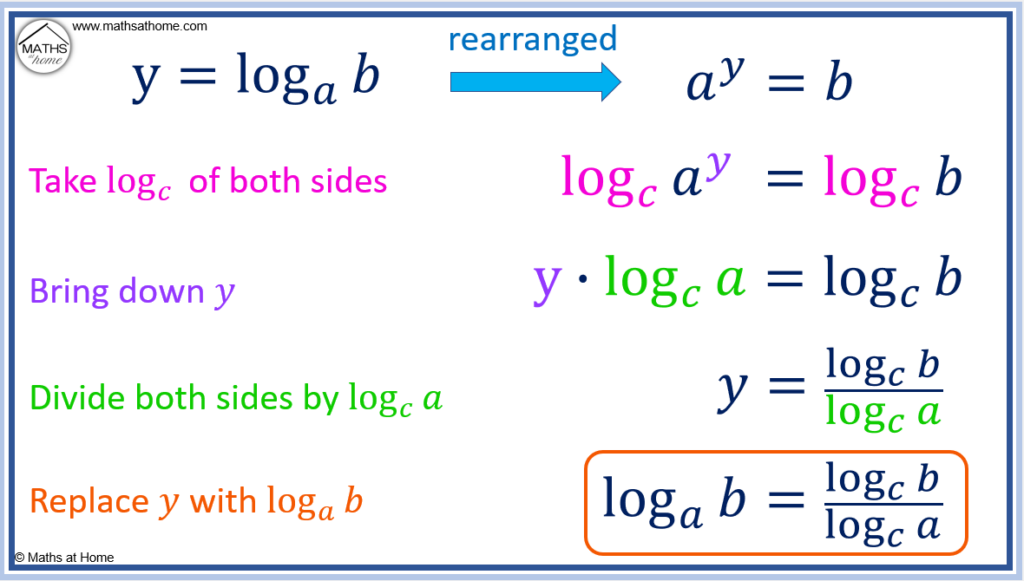
Proof of the Change of Base Formula for Logs

  1. Let logab = y such that ay=b.
  2. Take logc of both sides such that logcay=logcb.
  3. Bring down the power of y in front of the log to get ylogca=logcb.
  4. Divide both sides by logca to get y=[logcb]/[logca].
  5. Substitute y=logab such that logab=[logcb]/[logca].
proof of the logarithm change of base formula

How to Change the Base of a Log on a Calculator

To find the logarithm of a different base on a calculator, use the change of base button. Most calculators have the option to enter the base of a logarithm. This allows any logarithm to be evaluated after using the change of base formula.

For example, the log base 3 of 81 equals 4 .

Changing the base to base 5, the log base 3 of 81 equals the log base 5 of 81 over the log base 5 of 3.

Evaluating this on a calculator the log base 5 of 81 over the log base 5 of 3 equals 4.

change of base on a calculator

To enter logs with different bases on a Ti-84 calculator:

  1. Press the [math] key
  2. Scroll down and select ‘logBASE(‘ from the list
how to change log base on ti84 calculator

How to Change the Base of Exponents

To change the base of an exponent from base ‘a’ to base ‘c’, use the formula ab=cb⋅logc(a).

how to change the base of an exponent

a. to the b-th power equals c raised to the b times log base c of a. power

The change of base formula for exponents

For example, write 35 as a power of 2.

Here, a=3, b=5 and c=2.

Therefore 3 to the fifth power equals 2 raised to the 5 times log base 2 of 3 power.

We can approximate 5 times the log base 2 of 3 almost equals 7.92 and so 3 to the fifth power almost equals 2 raised to the 7.92 power

The change of base rule for exponents can be used to write any exponential as base e, where ‘e’ is Euler’s number, e almost equals 2.718.

For example, write 5x as an exponential with base e.

Here a=5, b=x and c=e.

Therefore 5 to the x-th power equals e raised to the x times log base e of 5 power.

Since log base e is the natural logarithm, ln, this can be written as 5 to the x-th power equals e raised to the x l n of 5 power.

Any exponential equation can be written as an exponential equation with base e using the formula: ax=exln(a).