How to Solve Quadratic Equations

Solving Quadratic Equations: Video Lesson

Quadratic Equation Solver

A quadratic equation of the form a. x squared plus b x plus c equals 0 can be solved using the quadratic formula where:

  • ‘a’ is the coefficient of of 𝑥2.
  • ‘b’ is the coefficient of 𝑥.
  • ‘c’ is the constant term

Enter the values of ‘a’, ‘b’ and ‘c’ into the quadratic equation solver below to calculate the values of 𝑥 that satisfy the equation.

For example, the quadratic equation 2 x squared plus x minus 3 equals 0 has ‘a’=2, ‘b’=1 and ‘c’=-3.

How to Solve Quadratic Equations

To solve a quadratic equation, the first step is to set one side of the equation equal to zero. The 3 ways to solve quadratic equations are factoring, completing the square or using the quadratic formula. If a quadratic equation cannot be factorised then completing the square or quadratic formula must be used.

If the quadratic has an 𝑥2 coefficient of 1 then it might be possible to solve it by factorising in the following way:

solving quadratic equations by factorising

If the quadratic has an 𝑥2 coefficient greater than 1 or cannot be factorised, the quadratic formula can be used:

solving quadratic equations using the quadratic formula

Here is a list of the methods that can be used to solve quadratic equations:

  • If 𝑥2 equals a number, square root both sides of the equation to solve it.
  • If the quadratic only contains 𝑥2 and 𝑥 terms, factorise the 𝑥 out and solve.
  • Try to factorise by finding two numbers that add to make the coefficient of 𝑥 and multiply to make the constant term. Solve by setting each factor to equal zero.
  • If the quadratic contains an 𝑥2 coefficient greater than 1, try to split the 𝑥 term and factorise by grouping.
  • If the quadratic cannot be factorised, complete the square and solve.
  • If the quadratic cannot be factorised, use the quadratic formula x equals the fraction with numerator negative b plus or minus the square root of b squared minus 4 a. c and denominator 2 a..

All quadratic equations can be solved using the quadratic formula so this method will always work for solving quadratic equations.

methods for solving quadratic equations

How to Solve Quadratic Equations using Square Roots

If a quadratic equation is of the form 𝑥2=k, square root both sides. The solutions are 𝑥=±√k. For example, if 𝑥2=4 then 𝑥=±2.

This simple type of quadratic equation can be identified as there is only an 𝑥2 and constant term in the equation.

solving quadratic equations using square roots

In this next example, 𝑥2 is equal to a non square number. We still square root both sides of the equation to obtain the solution.

For example, solve 𝑥2-5=0.

The first step is to add 5 to both sides of the equation so that 𝑥2=5.

The next step is to square root both sides of the equation so that 𝑥=±√5.

Evaluating ±√5 on a calculator, 𝑥≈-2.24 or 𝑥≈2.24.

solving a quadratic equation with square roots

How to Solve Quadratic Equations by Factoring

To solve a quadratic equation ‘𝑥2+b𝑥+c=0′ by factoring:
  1. Think of two numbers that add to make b and multiply to make c.
  2. Factor the quadratic as (𝑥+m)(𝑥+n)=0, where m and n are the two numbers from step 1.
  3. Solve the quadratic by setting each bracket equal to zero.
  4. The solutions are 𝑥=-m and 𝑥=-n.

Solving Quadratic Equations by Factoring: Example 1

For example, solve the quadratic equation x squared plus 4 x plus 3 equals 0 by factoring.

Here, b equals 4 and c equals 3.

Step 1. Think of two numbers that add to make b and multiply to make c

The numbers 1 and 3 add to make 4 and multiply to make 3.

how to solve quadratic equations by factoring

Step 2. Factor the quadratic as (𝑥+m)(𝑥+n)=0, where m and n are the two numbers from step 1

In step 1, the two numbers that add to make 4 and multiply to make 3 were 1 and 3.

Therefore the quadratic equation x squared plus 4 x plus 3 equals 0 can be factorised to open paren x plus 3 close paren times open paren x plus 1 close paren equals 0.

Step 3. Solve the quadratic by setting each bracket equal to zero

Either open paren x plus 3 close paren equals 0 or open paren x plus 1 close paren equals 0.

We find the values of 𝑥 that make each bracket equal zero.

For open paren x plus 3 close paren equals 0, the solution is x equals negative 3.

For open paren x plus 1 close paren equals 0 the solution is x equals negative 1.

Therefore the solutions to this quadratic equation are 𝑥=-3 and 𝑥=-1.

Solving Quadratic Equations by Factoring: Examples with Negatives

To solve a quadratic by factoring, think of two numbers that add to make the coefficient of 𝑥 and multiply to make the constant term.

For a quadratic x squared plus b x plus c equals 0, use the following rules to find the two numbers:

  • If b and c are both positive, the two numbers will both be positive
  • If c is positive but b is negative, the two numbers will both be negative
  • If c is negative, one number will be positive and one number will be negative

It is easier to factorise quadratics if you know what signs to expect in the brackets.

rules for factoring quadratics

Here are some examples of solving quadratic equations by factoring.

examples of solving quadratic equations by factoring
  • In example 1, x squared plus 6 x plus 8 equals 0.

Since b and c are positive, the quadratic will factor as open paren x plus close paren times open paren x plus close paren equals 0.

The two numbers that add to make 6 and multiply to make 8 are 4 and 2.

Therefore, the factored quadratic is open paren x plus 4 close paren times open paren x plus 2 close paren equals 0 and so, x equals negative 4 and x equals negative 2.

  • In example 2, x squared minus 5 x plus 6 equals 0.

Here, c is positive and b is negative so the quadratic will factor as open paren x minus close paren times open paren x minus close paren equals 0.

The two numbers that add to make -5 and multiply to make 6 are -3 and -2.

Therefore the factored quadratic is open paren x minus 3 close paren times open paren x minus 2 close paren equals 0 and so, x equals 3 and x equals 2.

  • In example 3, x squared plus 2 x minus 3 equals 0.

Here c is negative so the quadratic will factor as open paren x plus close paren times open paren x minus close paren equals 0.

The two numbers that add to make 2 and multiply to make -3 are 3 and -1.

Therefore the factored quadratic is open paren x plus 3 close paren times open paren x minus 1 close paren equals 0 and so, x equals negative 3 or x equals 1.

  • In example 4, x squared minus 3 x minus 10 equals 0.

Here c is negative so the quadratic will factor as open paren x plus close paren times open paren x minus close paren equals 0.

The two numbers that add to make -3 and multiply to make -10 are 2 and -5.

Therefore the factored quadratic is open paren x plus 2 close paren times open paren x minus 5 close paren equals 0 and so, x equals negative 2 and x equals 5.

How to Solve Quadratic Equations with Difference of Two Squares

Any quadratic equation of the form 𝑥2-a2=0 can be factored as (𝑥+a)(𝑥-a)=0 using the difference of two squares. Therefore the solutions are 𝑥=a and 𝑥=-a. For example, 𝑥2-25=0 factors as (𝑥+5)(𝑥-5)=0 and has solutions of 𝑥=5 and 𝑥=-5.

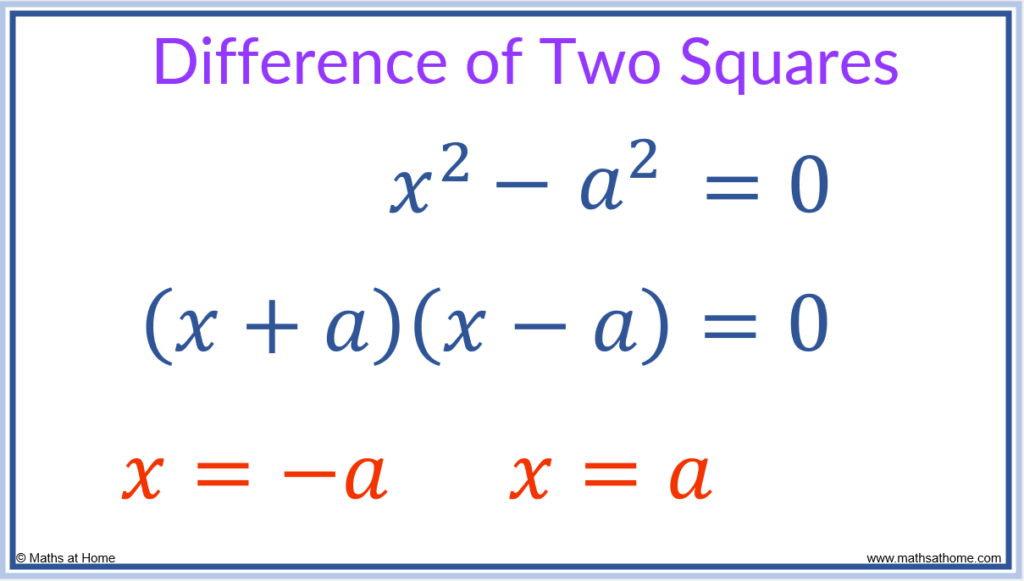
how to solve a quadratic using the difference of two squares

Quadratic equations of the form x squared minus a. squared equals 0 can be solved using the difference of two squares method.

To identify the difference of two squares, the quadratic should be made up of two terms separated by a minus sign.

For the quadratic x squared minus 25 equals 0, this is the same as x squared minus 5 squared equals 0.

Therefore this can be factored as open paren x plus 5 close paren times open paren x minus 5 close paren equals 0 and setting each bracket equal to zero to solve, x equals negative 5 and x equals 5.

example of difference of two squares

The difference of two squares can also be used to solve quadratics of the form k raised to the sub 2 power x squared minus a. squared equals 0. These quadratics will factor in the form open paren k x plus a. close paren times open paren k x minus a. close paren equals 0 which can be solved by setting each bracket equal to zero.

For example, solve 9 x squared minus 4 equals 0 using the difference of two squares.

This can be factorised as open paren 3 x plus 2 close paren times open paren 3 x minus 2 close paren equals 0.

The solutions are therefore x equals negative two thirds and x equals two thirds.

difference of two squares example

How to Solve Quadratic Equations with a Coefficient of 𝑥2 Greater than 1

To solve a quadratic equation with a leading coefficient greater than 1, use the quadratic formula or factorise and solve.

To factor a quadratic a𝑥2+b𝑥+c when a is greater than 1:

  1. Split the middle term into two terms that multiply to make the value of a×c.
  2. Factor the first two terms and the last two terms separately.
  3. Factor the whole expression by grouping.

For example, factor and solve the quadratic 2 x squared plus 7 x plus 6 equals 0.

In this quadratic, a. equals 2, b equals 7 and c equals 6

Step 1. Split the middle term into two terms that multiply to make the value of a×c

The middle term of 2 x squared plus 7 x plus 6 is 7 x. This will be split into two terms that when multiplied, equal the value of 2×6.

7 x is split into 4 x plus 3 x because 4×3=12, which is the same as 2×6.

step 1 of factoring a quadratic with a coefficient

Step 2. Factor the first two terms and the last two terms separately

The quadratic is currently written as 2 x squared plus 4 x plus 3 x plus 6.

The first two terms 2 x squared plus 4 x can be factorised as 2 x times open paren x plus 2 close paren and the last two terms 3 x plus 6 can be factorised as 3 times open paren x plus 2 close paren.

Therefore 2 x squared plus 4 x plus 3 x plus 6 can be written as 2 x times open paren x plus 2 close paren plus 3 times open paren x plus 2 close paren.

step 2 of factorising a quadratic with a leading coefficient greater than 1

Step 3. Factor the whole expression by grouping

In the equation 2 x times open paren x plus 2 close paren plus 3 times open paren x plus 2 close paren equals 0, there is a factor in common which is open paren x plus 2 close paren.

2 x times open paren x plus 2 close paren plus 3 times open paren x plus 2 close paren equals 0 can be grouped to get open paren 2 x plus 3 close paren times open paren x plus 2 close paren equals 0.

how to factorise a quadratic by grouping

Step 4. Solve the quadratic by setting each bracket equal to zero

The quadratic is currently written as open paren 2 x plus 3 close paren times open paren x plus 2 close paren equals 0.

Therefore either open paren 2 x plus 3 close paren equals 0 or open paren x plus 2 close paren equals 0.

Solving these equations, x equals negative three halves or x equals negative 2.

how to solve a quadratic where the leading coefficient is greater than 1

Examples of Solving Quadratic Equations with a>1 by Factoring

Here are some examples of solving quadratic equations with a leading coefficient greater than 1 using the factorising by grouping method.

EquationSplit the middle termFactorGroupSolutions
2 x squared minus 9 x plus 7 equals 02 x squared minus 2 x minus 7 x plus 7 equals 02 x times open paren x minus 1 close paren minus 7 times open paren x minus 1 close paren equals 0open paren 2 x minus 7 close paren times open paren x minus 1 close paren equals 0x equals seven halves,x equals 1
3 x squared plus 8 x plus 4 equals 03 x squared plus 6 x plus 2 x plus 4 equals 03 x times open paren x plus 2 close paren plus 2 times open paren x plus 2 close paren equals 0open paren 3 x plus 2 close paren times open paren x plus 2 close paren equals 0x equals negative two thirds,x equals negative 2
5 x squared minus 22 x plus 8 equals 01 lines Line 1: 5 x squared minus 20 x minus 2 x plus 8 equals 01 lines Line 1: 5 x times open paren x minus 4 close paren minus 2 times open paren x minus 4 close paren equals 01 lines Line 1: open paren 5 x minus 2 close paren times open paren x minus 4 close paren equals 0x equals two fifths,x equals 4
8 x squared minus 14 x plus 5 equals 08 x squared minus 4 x minus 10 x plus 5 equals 04 x times open paren 2 x minus 1 close paren minus 5 times open paren 2 x minus 1 close paren equals 0open paren 4 x minus 5 close paren times open paren 2 x minus 1 close paren equals 0x equals five fourths,x equals one half

How to Solve Quadratic Equations by Completing the Square

All quadratic equations can be solved by completing the square and then rearranging the equation for 𝑥. For example, the equation 𝑥2+4𝑥+1=0 can be written as (𝑥+2)2-3=0. Adding 3 to both sides of the equation, (𝑥+2)2=3. Taking the square root, 𝑥+2=±√3 and so, 𝑥=-2±√3.

To solve an equation by completing the square, follow these steps:

  1. Complete the square, writing 𝑥2+b𝑥+c=0 in the form open paren x plus b over 2 close paren squared minus open paren b over 2 close paren squared plus c equals 0
  2. Move the constant term to the other side of the equals sign
  3. Square root both sides
  4. Solve for 𝑥

For example, complete the square and solve, x squared plus 4 x plus 1 equals 0.

Step 1. Complete the square

To complete the square, write x squared plus b x plus c equals 0 in the form open paren x plus b over 2 close paren squared minus open paren b over 2 close paren squared plus c equals 0.

In x squared plus 4 x plus 1 equals 0, b equals 4 and c equals 1.

Therefore completing the square using the above formula, x squared plus 4 x plus 1 equals 0 becomes open paren x plus four halves close paren squared minus four halves squared plus 1 equals 0.

This simplifies to open paren x plus 2 close paren squared minus 3 equals 0.

formula for completing the square

Completing the square has now been completed and now we solve the equation by rearranging for 𝑥.

Step 2. Move the constant term to the other side of the equals sign

We add 3 to both sides of the equation so that open paren x plus 2 close paren squared minus 3 equals 0 becomes open paren x plus 2 close paren squared equals 3

Step 3. Square root both sides

Taking the square root of both sides, open paren x plus 2 close paren squared equals 3 becomes x plus 2 equals plus or minus the square root of 3.

Remember, when taking the square root, there are two solutions. A positive and a negative solution.

Step 4. Solve for 𝑥

Simply subtract two from both sides so that x plus 2 equals plus or minus the square root of 3 becomes x equals negative 2 plus or minus the square root of 3.

The two solutions are x sub 1 equals negative 2 minus the square root of 3 and x sub 2 equals negative 2 plus the square root of 3.

solving a quadratic equation by completing the square

Example of Solving a Quadratic Equation with a Leading Coefficient Greater than 1 using Completing the Square

If a quadratic equation has a leading coefficient greater than 1, first factor this coefficient out before completing the square.

For example, solve 2 x squared minus 12 x plus 3 equals 0 by completing the square.

Since the leading coefficient is 2, factor this out to get 2 times open paren x squared minus 6 x plus 1.5 close paren equals 0.

We can now divide both sides by 2 to get x squared minus 6 x plus 1.5 equals 0.

Now completing the square we get open paren x minus 3 close paren squared minus 7.5 equals 0.

Solving for 𝑥, we get x equals 3 plus or minus the square root of 7.5.

Examples of Solving Quadratic Equations by Completing the Square

Here are some examples of solving quadratic equations by completing the square

Quadratic EquationComplete the SquareSolutions
x squared plus 6 x minus 5 equals 0open paren x plus 3 close paren squared minus 14 equals 0x equals negative 3 plus or minus the square root of 14
x squared minus 4 x plus 3 equals 0open paren x minus 2 close paren squared minus 1 equals 0x equals 1 comma x equals 3
x squared plus 3 x minus 1 equals 0open paren x plus 1.5 close paren squared minus 3.25 equals 0x equals negative 1.5 plus or minus the square root of 3.25
2 x squared plus 8 x minus 2 equals 02 times open paren x plus 2 close paren squared minus 10 equals 0x equals negative 2 plus or minus the square root of 5

How to Solve Quadratic Equations with the Quadratic Formula

To solve a quadratic equation a𝑥2+b𝑥+c=0, use the quadratic formula 𝑥=[-b±√(b2-4ac)]/2a.

The quadratic formula is the most reliable method for solving a quadratic equation. It can always be used to obtain solutions.

x equals the fraction with numerator negative b plus or minus the square root of b squared minus 4 a. c and denominator 2 a.

The quadratic formula

To use the quadratic formula, first find the values of -b, b2-4ac and 2a so that these three values can be entered directly into the formula.

For example, solve the quadratic equation 2 x squared minus 5 x plus 3 equals 0.

Here, a. equals 2, b equals negative 5 and c equals 3.

Therefore negative b equals 5, b squared minus 4 a. c equals 1 and 2 a. equals 4.

how to use the quadratic formula to solve quadratic equations

Entering these values into the quadratic formula, x equals the fraction with numerator 5 plus or minus the square root of 1 and denominator 4.

Therefore x sub 1 equals the fraction with numerator 5 minus 1 and denominator 4 and x sub 2 equals the fraction with numerator 5 plus 1 and denominator 4.

x sub 1 equals 1 and x sub 2 equals 1.5.

Solving Quadratic Equations with the Quadratic Formula Examples

Here are some examples of using the quadratic formula to solve quadratic equations:

EquationabcQuadratic FormulaSolutions
3 x squared plus 5 x plus 1 equals 0351x equals the fraction with numerator negative 5 plus or minus the square root of 13 and denominator 6x almost equals negative 1.43, x almost equals negative 0.232
2 x squared plus 3 x minus 5 equals 023-5x equals the fraction with numerator negative 3 plus or minus the square root of 49 and denominator 4x almost equals negative 2.5, x almost equals 1
2 x squared minus 5 x plus 1 equals 02-51x equals the fraction with numerator 5 plus or minus the square root of 17 and denominator 4x almost equals 0.219, x almost equals 2.28
x squared plus 3 x minus 1 equals 013-1x equals the fraction with numerator negative 3 plus or minus the square root of 13 and denominator 2x almost equals 3.30, x almost equals 0.303
negative x squared plus 4 x plus 2 equals 0-142x equals the fraction with numerator negative 4 plus or minus the square root of 24 and denominator negative 2x almost equals negative 0.449, x almost equals negative 4.45

Solving Quadratic Equations Not Written in Standard Form

To solve a quadratic equation that is not written in standard form, first rearrange it so that it is in the form a𝑥2+b𝑥+c=0. Then it can be factorised or the quadratic formula can be used to solve it.

Solving a Quadratic Equation Not Written in Standard Form: Example 1

For example, solve the quadratic equation the fraction with numerator 4 and denominator x minus 2 equals x plus 1.

The first step is to multiply both sides of the equation by the denominator of x minus 2.

The equation becomes 4 equals open paren x plus 1 close paren times open paren x minus 2 close paren.

Expanding the brackets, 4 equals x squared minus x minus 2.

Subtracting 4 from both sides, 0 equals x squared minus x minus 6.

x squared minus x minus 6 equals 0 can be factorised to give open paren x minus 3 close paren times open paren x plus 2 close paren equals 0.

Therefore x equals 3 or x equals negative 2.

Solving a Quadratic Equation Not Written in Standard Form: Example 2

Solve the quadratic equation, x times open paren x plus 4 close paren equals 4 times open paren x plus 16 close paren.

Expanding the brackets, x squared plus 4 x equals 4 x plus 64.

Subtracting 4 x from both sides, x squared equals 64.

We can solve this by finding the square root of both sides so that x equals plus or minus 8.

Solving a Quadratic Equation when given ‘y’

When given y in a quadratic equation, the corresponding values of x can be found by rearranging the equation equal to zero and solving for x.

For example, in the equation y equals x squared plus 5 x plus 3, find the values of x for which y equals negative 3.

Substituting y equals negative 3 into the equation, negative 3 equals x squared plus 5 x plus 3.

Adding 3 to both sides, 0 equals x squared plus 5 x plus 6.

Factorising, 0 equals open paren x plus 2 close paren times open paren x plus 3 close paren.

Therefore, x equals negative 2 and x equals negative 3.

How to Solve Quadratic Equations by Graphing

For a quadratic equation that is set equal to zero, the solutions are the x-axis intercepts of its graph. Graphing a quadratic is one way to find the x-intercepts. These can be read off from the graph as the solutions to the quadratic equation.

For example, the graph of y equals x squared plus x minus 12 is shown below.

solutions to a quadratic equation by graphing

The graph has x-intercepts of x equals negative 4 and x equals 3.

These are the solutions of x squared plus x minus 12 equals 0.

Solving Quadratic Equations with Complex Solutions

For a quadratic equation of the form a𝑥2+bx+c=0, complex solutions will exist if b2-4ac<0. This is because it is not possible to obtain real answers when finding the square root of a negative number in the quadratic formula. Instead, the solutions will contain imaginary components.

For example, find the solutions to x squared plus 2 x plus 5 equals 0.

a=1, b=2 and c=5.

Therefore, b squared minus 4 a. c equals 4 minus 20 equals negative 16.

Therefore, the quadratic formula, x equals the fraction with numerator negative b plus or minus the square root of b squared minus 4 a. c and denominator 2 a. becomes x equals the fraction with numerator negative 2 plus or minus the square root of negative 16 and denominator 2.

Since the square root of negative 1 equals i, the square root of negative 16 equals 4 i.

Therefore x equals the fraction with numerator negative 2 plus or minus the square root of negative 16 and denominator 2 simplifies to x equals the fraction with numerator negative 2 plus or minus 4 i and denominator 2 and so, x equals negative 1 plus or minus 2 i.