How to Solve an Exponential Equation

How to Solve an Exponential Equation: Video Lesson

How to Solve an Exponential Equation

To solve an exponential equation, take logs of both sides of the equation and bring the power down in front of the log. The resulting linear equation can be solved for x. For example, solve 5x=13. Taking logs, log(5x)=log(13). Then xlog(5)=log(13). Now solving for x, x = log(13)/log(5). Therefore, x≈1.59.

Solving an Exponential Equation: Example 1

Solve 5x = 13.

Step 1. Take logs of both sides

5x = 13 becomes log(5x) = log(13).

Step 2. Bring down the power in front of the log

The power of x can be written in front of the log so that log(5x) = log(13) becomes xlog(5) = log(13).

how to solve an exponential equation

Step 3. Solve the resulting equation for x

xlog(5) = log(13) can be solved for x by dividing both sides of the equation by log(5).

x equals log 13 over log 5

This can be evaluated on a calculator to get 𝑥 ≈ 1.59.

Solving an Exponential Equation: Example 2

Solve 32x = 0.51

Step 1. Take logs of both sides

32x = 0.51 becomes log(32x) = log(0.51).

Step 2. Bring down the power in front of the log

The power of 2x can be written in front of the log so that log(32x) = log(0.51) becomes 2xlog(3) = log(0.51).

how to solve an exponential equation with a negative answer

Step 3. Solve the resulting equation for x

2xlog(3) = log(0.51) can be solved by dividing both sides by 2log(3).

x equals log 0.51 over 2 log 3

This can be evaluated as 𝑥 ≈ -0.306.

How to Solve Exponential Equations with Different Bases

To solve an exponential equation with different bases:

  1. Take logarithms of both sides of the equation.
  2. Bring down the exponent in front of the logs.
  3. Expand and collect x terms.
  4. Factorise and solve for x.
steps to solve an exponential equation

For example solve the exponential equation 5𝑥 = 2𝑥+2.

Step 1. Take logarithms of both sides

Write each side of the equation inside a log.

5𝑥 = 2𝑥+2 becomes log(5𝑥) = log(2𝑥+2).

step 1 of solving exponential equations

Step 2. Bring down the exponent in front of the logs

Use the log law log(ab) = blog(a) to bring the powers down in front of the logs on both sides.

log(5𝑥) = log(2𝑥+2) becomes 𝑥log(5) = (𝑥+2)log2.

step 2 of solving an exponential equation

Step 3. Expand and collect 𝑥 terms

Expanding the bracket on the right hand side of the equation, (𝑥+2)log2 becomes 𝑥log2 +2log2.

Now the bracket is expanded, the equation becomes 𝑥log5 = 𝑥log2 + 2log.

We need to gather the 𝑥 terms all together on one side of the equation. We subtract 𝑥log2 from both sides of the equation which gives us:

𝑥log5 – 𝑥log2 = 2log2.

step 3 of solving exponential equations

Step 4. Factorise and solve for 𝑥

Now the 𝑥 terms are on one side of the equation, we can factorise 𝑥 out.

𝑥log5 – 𝑥log2 becomes 𝑥(log5 – log2).

Therefore the equation becomes 𝑥(log5-log2) = 2log2.

To solve for 𝑥, we simply divide both sides of the equation by (log5-log2).

Therefore x equals the fraction with numerator 2 log 2 and denominator open paren log 5 minus log 2 close paren.

This is the exact answer but it can be evaluated on a calculator as 𝑥 ≈ 1.51.

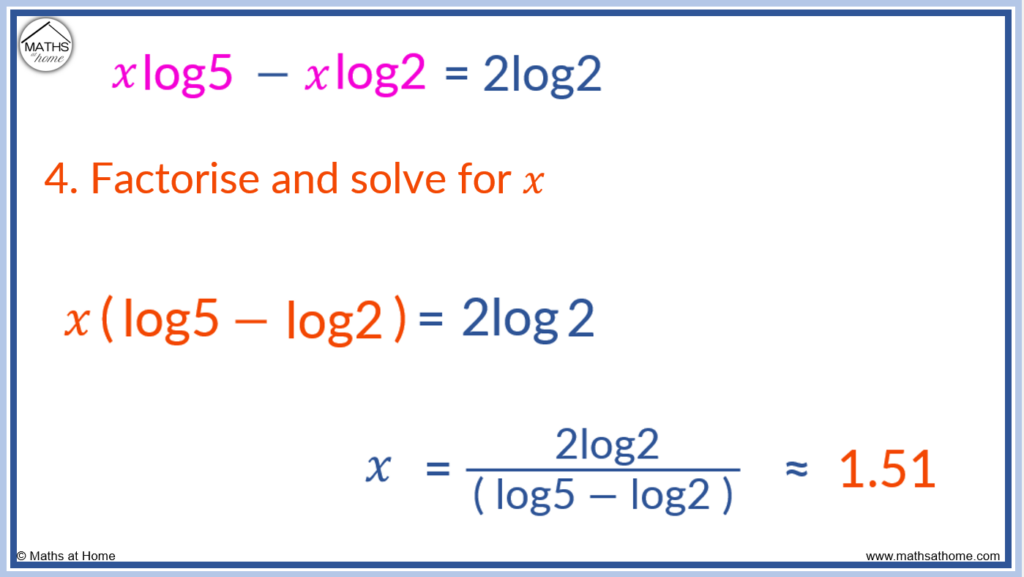
step 4 of solving an exponential equation

The image below shows a summary of how to solve the exponential equation in steps.

example of how to solve an exponential equation

Solving Exponential Equations with e

To solve an exponential equation that has a base of e, take the natural logarithm of both sides of the equation. Then solve the resulting equation for x. For example, solve e2x=5. Taking the natural logarithm of both sides, 2x = ln(5). Dividing both sides by 2, x = ln(5)/2, which approximately equals 0.805.
how to solve an exponential equation with e

The natural logarithm, ln(x) is the inverse function to ex.

Therefore ln(ex) = x.

In this example, e2x = 5.

Taking the natural logarithm of both sides, we get:

ln(e2x) = ln(5)

Here, ln and e cancel out so that:

2x = ln(5)

Now we solve the resulting equation for x by dividing both sides by 2.

x = ln(5)/2

This is the exact answer and evaluating it on a calculator, we get x ≈ 0.805.

Here is another example.

Solve the exponential equation 5e3x = 31.

When solving exponential equations with e, the natural logarithm ln(x) is used.

However it is important to first remove any coefficients from in front of the e.

We first divide both sides by 5 to get:

e3x = 6.2

example of solving an exponential equation with e

Now the coefficient has been removed, the natural logarithm can be taken.

3x = ln(6.2)

Now we can solve for x by dividing both sides by 3.

x = ln(6.2)/3

Evaluating this on a calculator 𝑥 ≈ 0.608.

How to Solve Exponential Equation with the Same Base

If an exponential equation can be written so that both bases are the same, the equation can be solved by comparing the exponents. For example, 2x+4=8x can be written as 2x+4=(23)x. Expanding, this becomes 2x+4=23x. Setting the exponents equal to each other, x+4=3x and so x = 2.

Solving Exponential Equations with the Same Base: Example 1

In this example, 8 is a power of 2 and so, it is possible to write both sides of the equation with the same base of 2.

how to solve an exponential with the same base

Solving Exponential Equations with the Same Base: Example 2

Solve 52x = 51-x

In this example, the bases are already equal. The bases are both 5.

Therefore the exponents must be equal to each other.

2x = 1 – x

Solve this equation for x by adding x to both sides.

3x = 1

Solve for x by dividing both sides of the equation by 3.

x = 1/3

Solving Exponential Equations with the Same Base: Example 3

Solve 9 raised to the 2 x minus 1 power equals the square root of 3.

Firstly, write both sides of the equation with the same base.

We can use 9 = 32 and √3 = 31/2 to help us.

3 squared raised to the exponent 2 x minus 1 end exponent equals 3 raised to the one half power

Now expanding, this becomes:

3 raised to the 4 x minus 2 power equals 3 raised to the one half power

Now the bases are equal, the exponents must be equal.

4𝑥 – 2 = 0.5

Now we solve for 𝑥. We add 2 to both sides:

4𝑥 = 2.5

Now we divide by 4 to get:

𝑥 = 0.625

How to Solve Exponential Equations with Fractional Bases

To solve exponential equations with fractional bases:

  1. Find a common base.
  2. Equate the exponents.

Solving an Exponential Equation with a Fractional Base: Example 1

Solve 1 lines Line 1: one fourth to the x-th power equals 8

Step 1. Find a common base

Comparing both sides of the equation, 4 and 8 are both powers of 2.

one fourth to the x-th power equals 2 to the negative 2 power to the x-th power and 2 to the negative 2 power to the x-th power equals 2 raised to the negative 2 x power.

8 = 23.

how to solve an exponential equation with a fractional base

1 lines Line 1: one fourth to the x-th power equals 8 becomes 2 raised to the negative 2 x power equals 2 cubed

Step 2. Equate the exponents

Now that the bases are equal, the exponents can be equated.

-2𝑥 = 3

This can be solved for 𝑥 by dividing both sides by -2.

x equals negative three halves

Solving an Exponential Equation with a Fractional Base: Example 2

Solve 1 lines Line 1: two thirds raised to the x plus 6 power equals open paren 8 over 27 close paren raised to the 3 x power

Step 1. Find a common base

In this example, we can compare the fractions on each base.

8 = 23 and 27 = 33.

Therefore open paren 8 over 27 close paren equals two thirds cubed.

Therefore1 lines Line 1: two thirds raised to the x plus 6 power equals open paren 8 over 27 close paren raised to the 3 x power can be written astwo thirds raised to the x plus 6 power equals open paren two thirds cubed close paren raised to the exponent 3 x end exponent.

This simplifies totwo thirds raised to the x plus 6 power equals two thirds raised to the 9 x power.

how to solve exponential equations with fractions

Step 2. Equate the exponents

Now that the bases are the same, the exponents can be equated.

𝑥 + 6 = 9𝑥

This equation can be solved by first subtracting 𝑥 from both sides to get 6 = 8𝑥.

Solving for 𝑥, the solution is x equals three fourths.

Solving an Exponential Equation with a Fractional Base: Example 3

For exponential equations involving fractions, where no common base can be found, take logarithms of both sides. Then bring down the power in front of the log and solve for 𝑥.

Solve four fifths raised to the 2 x power equals 12

Step 1. Take logs of both sides

the log of four fifths raised to the 2 x power equals log 12

Step 2. Bring down the power in front of the log

2 x log four fifths equals log 12

Step 3. Solve for 𝑥

x equals log 12 over 2 log four fifths

Evaluating this on a calculator, 𝑥 = -5.57.

How to Solve Exponential Equations Involving Quadratics

An exponential equation will lead to a quadratic equation if one base is the square of the other base. For example the equation 9x-5(3x)+6=0 can be written as (3x)2-5(3x)+6=0. Substituting k=3x, this leads to the quadratic equation k2-5k+6=0. This quadratic equation can be solved to find x.

The steps for solving an exponential equation involving a quadratic are:

  1. Write one base as the other base squared
  2. Substitute this base for k to form a quadratic
  3. Solve the resulting quadratic for k
  4. Solve the exponential equation for x

Solving an Exponential Equation Leading to a Quadratic: Example 1

For example solve 9 to the x-th power minus 5 times open paren 3 to the x-th power close paren plus 6 equals 0.

We know that this equation will lead to a quadratic because 9x is the square of 3x.

Step 1. Write one base as the other base squared

9x = (32)x which can be written as (3x)2.

Therefore 9x = (3x)2.

Therefore 9 to the x-th power minus 5 times open paren 3 to the x-th power close paren plus 6 equals 0 can be written as 3 to the x-th power squared minus 5 times open paren 3 to the x-th power close paren plus 6 equals 0.

Step 2. Substitute this base for k to form a quadratic

We can substitute k = 3x in the equation 3 to the x-th power squared minus 5 times open paren 3 to the x-th power close paren plus 6 equals 0 so that the quadratic equation of k squared minus 5 k plus 6 equals 0 is formed.

how to solve an exponential equation leading to a quadratic

Step 3. Solve the resulting quadratic for k

k squared minus 5 k plus 6 equals 0 can be factorised to give (k-3)(k-2) = 0.

Therefore k = 3 or k = 2.

Step 4. Solve the exponential equations for x

Since we set k = 3x, if k = 3 or k = 2 then 3x = 3 or 3x = 2.

If 3x = 3 then x = 1.

If 3x = 2 then we can solve this exponential equation with logs.

log(3x)=log(2) and so, xlog(3) = log(2).

Therefore x equals log 2 over log 3.

Evaluating this, x almost equals 0.631.

Solving an Exponential Equation Leading to a Quadratic: Example 2

Solve 25 to the x-th power minus 5 raised to the x plus 1 power plus 4 equals 0.

Step 1. Write one base as the other squared

25x = (5x)2

Therefore 25 to the x-th power minus 5 raised to the x plus 1 power plus 4 equals 0 becomes 5 to the x-th power squared minus 5 raised to the x plus 1 power plus 4 equals 0.

We can write 5 to the x-th power squared minus 5 raised to the x plus 1 power plus 4 equals 0 as 5 to the x-th power squared minus 5 times 5 to the x-th power plus 4 equals 0.

Step 2. Substitute this base for k to form a quadratic

Let k = 5x so that 5 to the x-th power squared minus 5 times 5 to the x-th power plus 4 equals 0 can be written as k squared minus 5 k plus 4 equals 0.

Step 3. Solve the resulting quadratic for k

k squared minus 5 k plus 4 equals 0 can be written as (k – 4)(k – 1) = 0.

Therefore k = 4 or k = 1.

Step 4. Solve the exponential equations for x

Since k = 5x, the solutions of k = 4 and k = 1 become 5x = 4 and 5x = 1.

If 5x = 4, x equals log 4 over log 5almost equals 0.861 period

If 5x = 1, 𝑥 = 0