Calculate a Bearing From an Angle: Video Lesson
Calculate a Bearing Using Trigonometry: Video Lesson
What is a Bearing in Mathematics?
In mathematics, a bearing is defined as an angle measured clockwise from north. Bearings are usually written as a three-figure bearing. For example, the angle 50° from north is written as 050°.
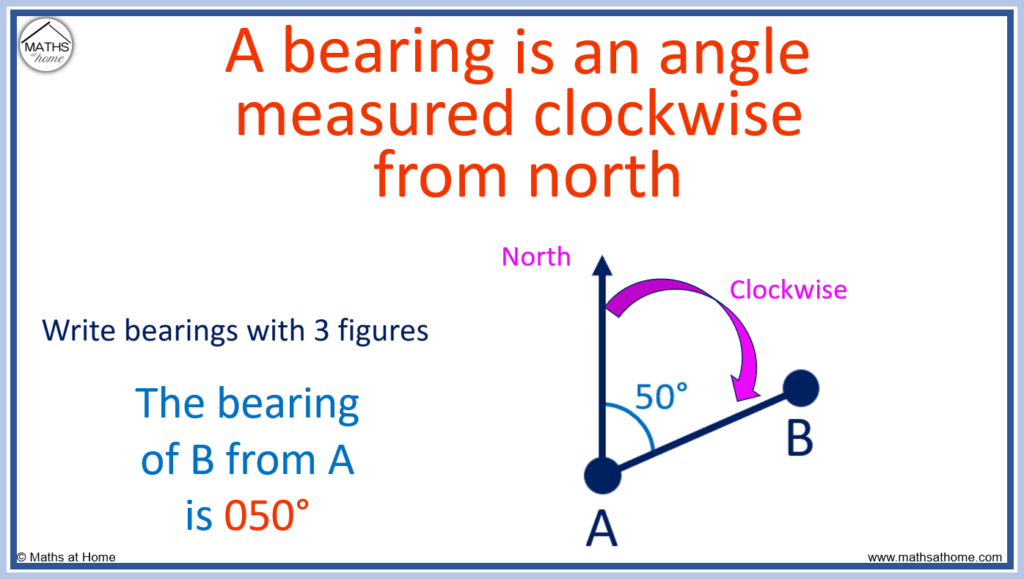
A bearing is always defined as an angle clockwise from north. Bearings are important for navigation in 2-dimensions such as when using maps. Bearings are useful because the angle is always relative to north and therefore they provide a consistent measurement of direction.
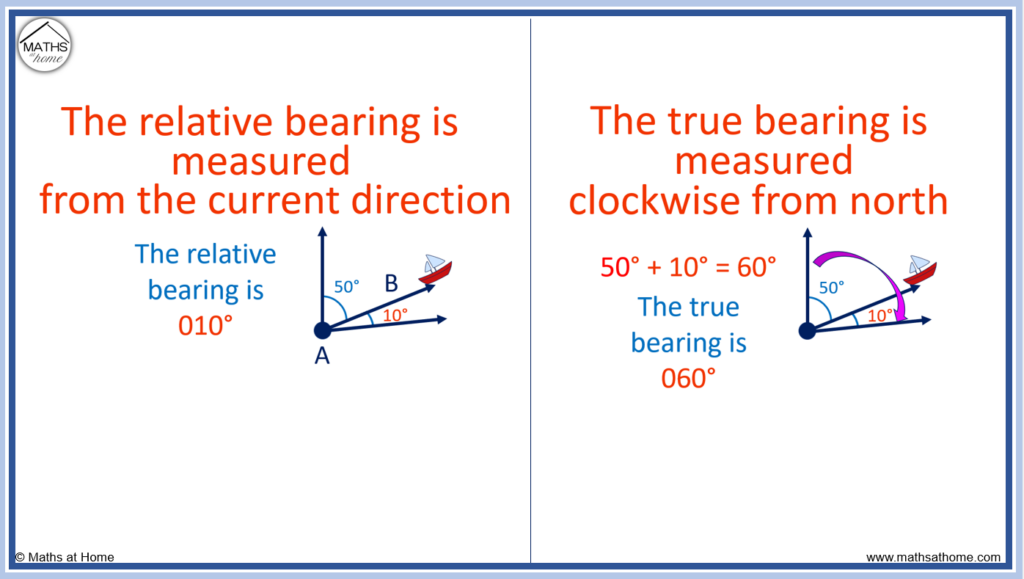
The true bearing is the angle measured clockwise from north. The true bearing is often referred to simply as the bearing.
The relative bearing is the angle between the direction of travel and some other direction. This angle is measured clockwise from the current direction.
For example, a ship is currently travelling on a bearing of 050°. A relative bearing of 010° is made from the ship’s current direction.
Whilst the relative bearing is 010°, the true bearing of this new direction is 060° because the ship is already on a bearing of 50° and 50° + 10° = 60°.
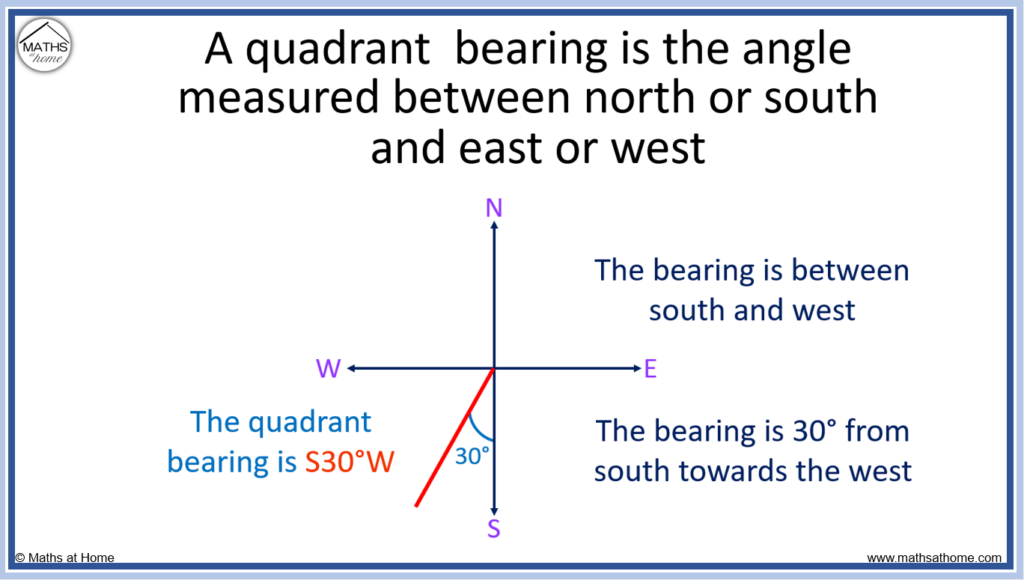
Alternatively, bearings can be written as quadrant bearings.
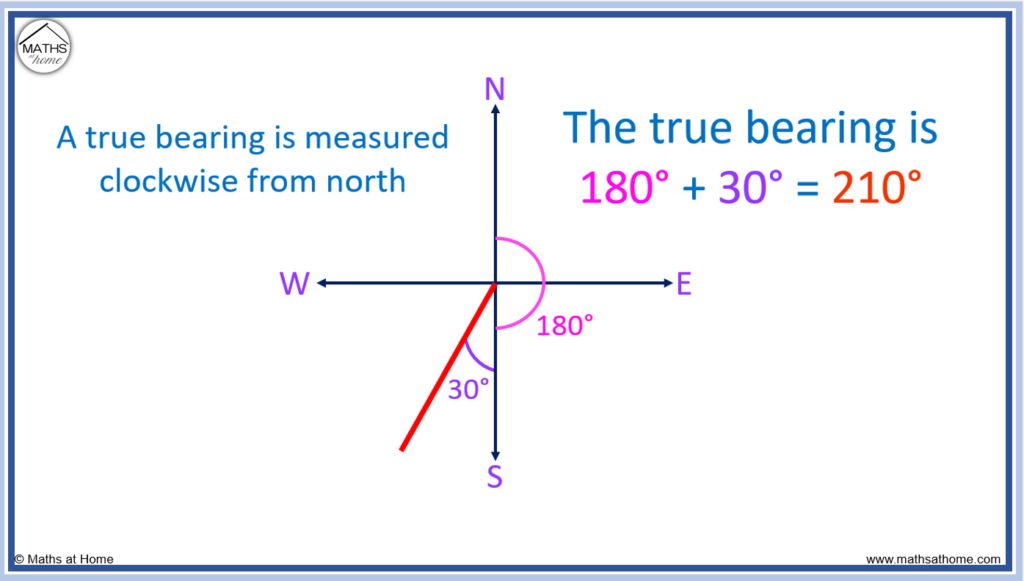
A quadrant bearing is the angle made between a north or south direction and an east or west direction. North or south is written first, then the angle, then east or west. For example, a quadrant bearing of S30°W means to start facing south then make a 30° angle towards the west.
In a quadrant bearing, the angle is always measured as the smallest angle from either north or south. This angle can be either clockwise or counter-clockwise depending on which direction is the nearest. The angle of a true bearing is always measured from north and the angle is always given in a clockwise direction.
Therefore a quadrant bearing of S30°W would convert to a true bearing of 210°. This is because the angle measured clockwise from north would include the 180° to face south, then a further 30°. In total, 180° + 30° = 210°.

To convert a quadrant bearing to a true bearing, first draw a diagram of the quadrant bearing. The true bearing is the angle measured clockwise from north to this bearing. Use the fact that from north, east is 90°, south is 180° and west is 270°. Then add or subtract the quadrant bearing angle from these values depending on if the quadrant bearing is measured clockwise or counter-clockwise respectively.
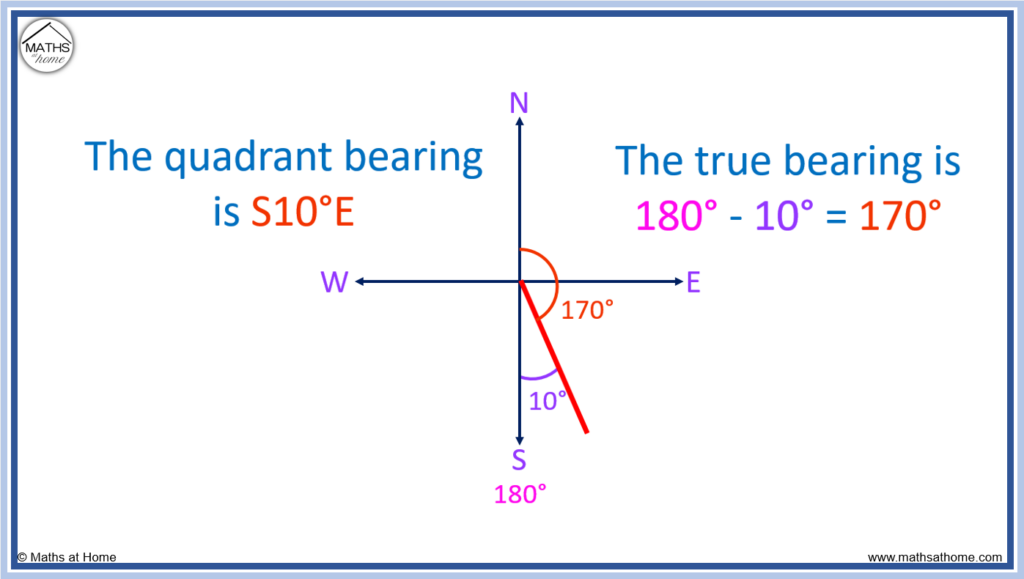
For example, a quadrant bearing of S10°E converts to a true bearing of 170°.
This is because south is 180° but we must go back 10° to get to S10°E. Therefore 180° – 10° = 170°.
Here are some examples of converting between quadrant bearings and true bearings.
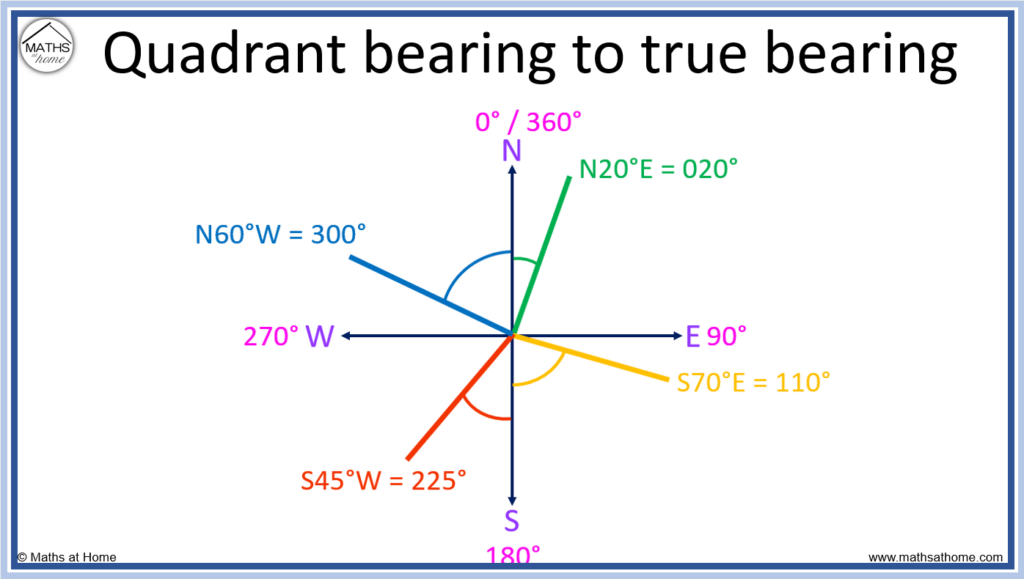
| Quadrant Bearing | Conversion calculation | True Bearing |
| N20°E | 0° + 20° | 020° |
| S70°E | 180° – 70° | 110° |
| S45°W | 180° + 45° | 225° |
| N60°W | 360° – 60° | 300° |
How to Calculate a Bearing
To calculate a bearing, find the angle clockwise from north. Start by drawing a vertical line representing north at the first location. Draw a line connecting the start location to the end location. Measure the clockwise angle between the north line and this line.
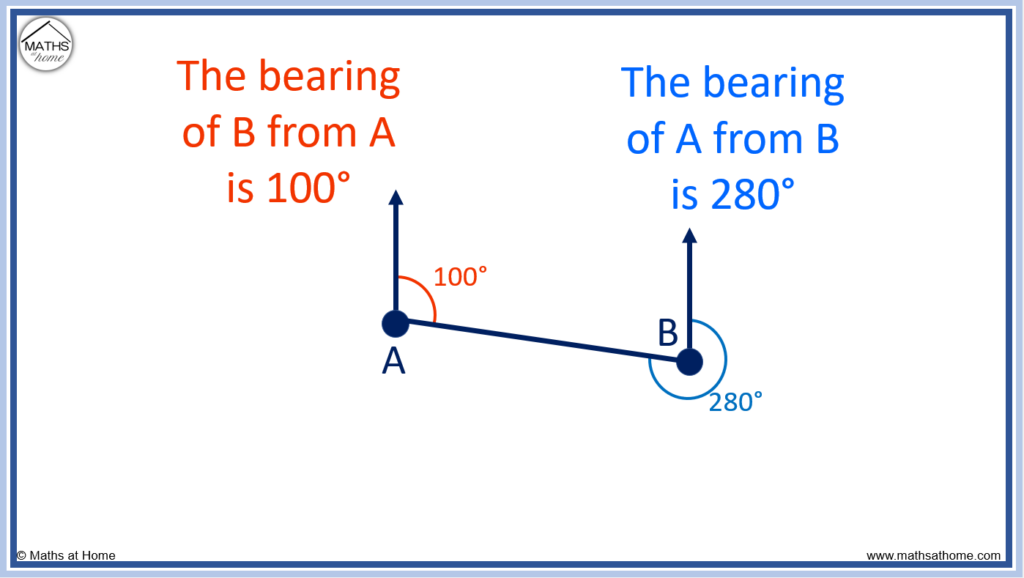
For example, the bearing from A to B is 100°. This is the angle from north clockwise to B.
The bearing from B to A is 280°. This is the angle from north clockwise to A.
There are 3 rules to follow when measuring a bearing:
- Always measure the angle in a clockwise direction
- Always measure the angle from north
- Always give a 3-figure bearing (E.g. 030° instead of 30°)
How to Calculate a Bearing From an Angle
To find a bearing from a given angle, use the following angle facts:
- Co-interior ‘c’ angles add to 180°.
- Alternate ‘z’ angles are equal.
- Angles on a straight line add to 180°.
- Angles in a full turn add to 360°.
Bearing From an Interior Angle
Interior angles add to 180°. If given the bearing from B to A, the bearing from A to B can be found using interior angles. Subtract the bearing of B to A from 180° to find the missing interior angle, then use the fact that angles in a full turn add to 360° to find the bearing of A to B.
For example, the bearing of B from A is 050°. Find the bearing of A from B.
Drawing a north on both points A and B, the norths form parallel lines and a co-interior angle are formed.
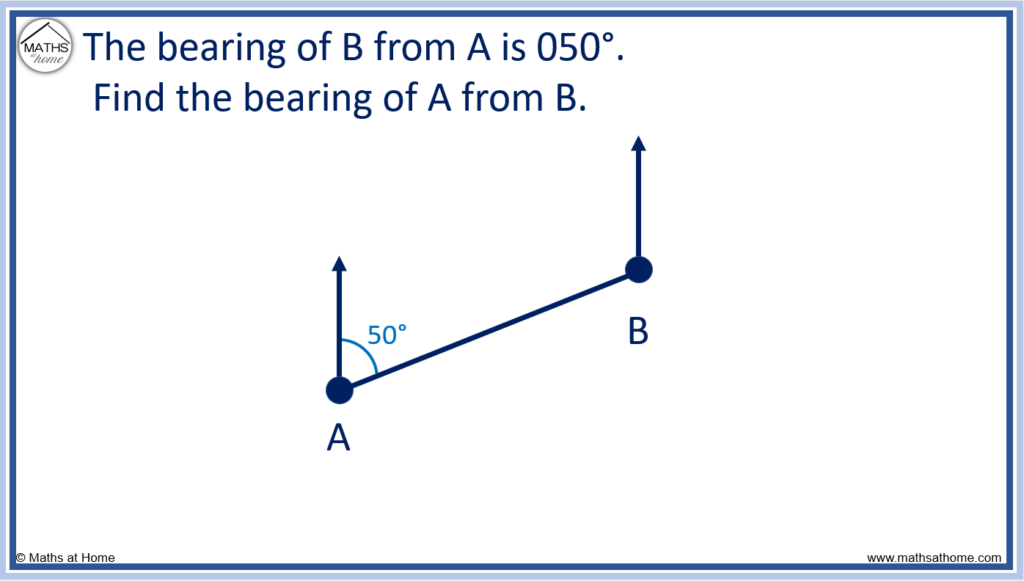
The bearing of 050° and the co-interior angle formed must total 180°. The counter-clockwise angle from B to A is 130°.
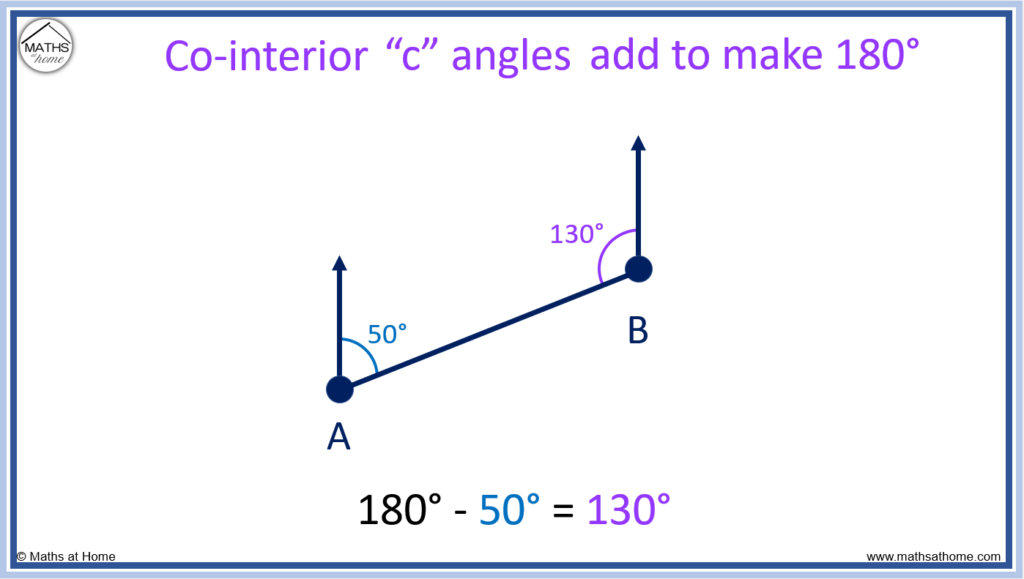
However a bearing must always be measured clockwise from north. 130° is counter-clockwise from north.
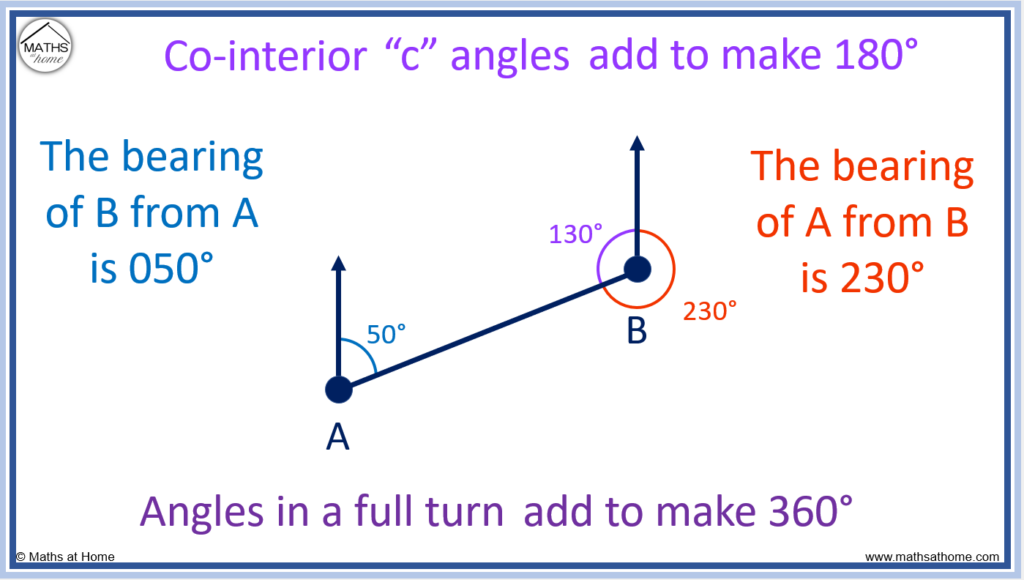
The clockwise angle on the other side is needed. Use the angle fact that angles in a full turn add to 360°.
To work the bearing, subtract 130° from 360°.
360° – 130° = 230° and so, the bearing of A from B is 230°.
Here is another example of bearings using interior angles.
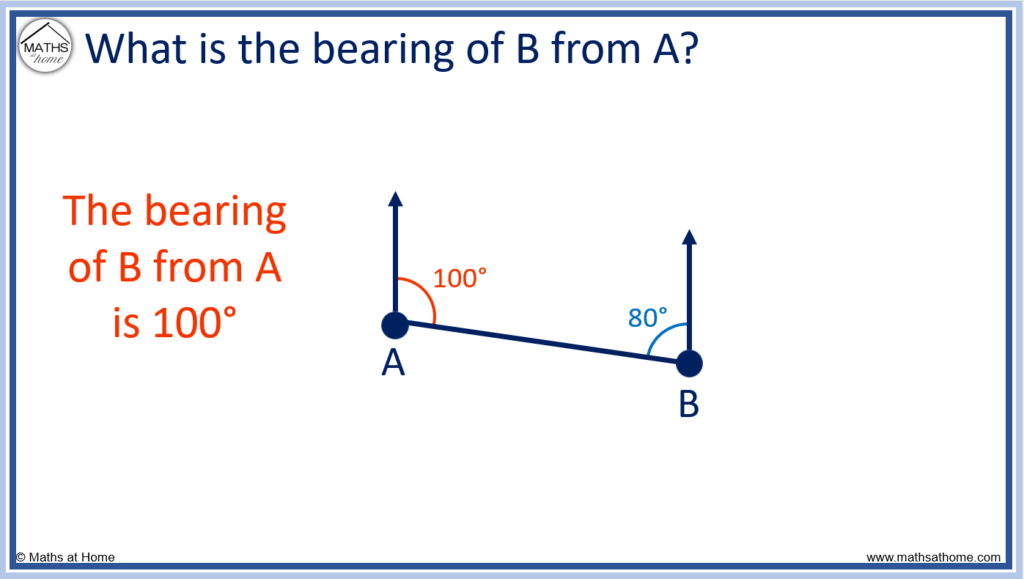
For example, find the bearing of B from A.
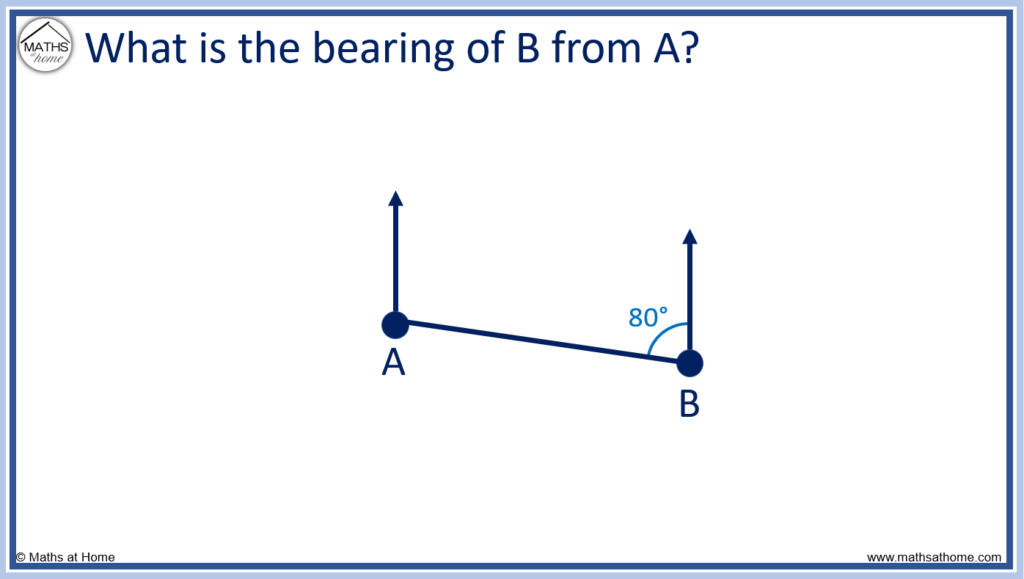
In this case, the bearing of B from A and the given angle of 80° both form interior angles. Therefore they both add to 180°.
180° – 80° = 100° and so, the bearing of B from A is 100°.
Bearings with Alternate Angles
Alternate angles are equal and are recognised by the ‘z’ shape made between the two angles. These angle facts can be used to calculate bearings.
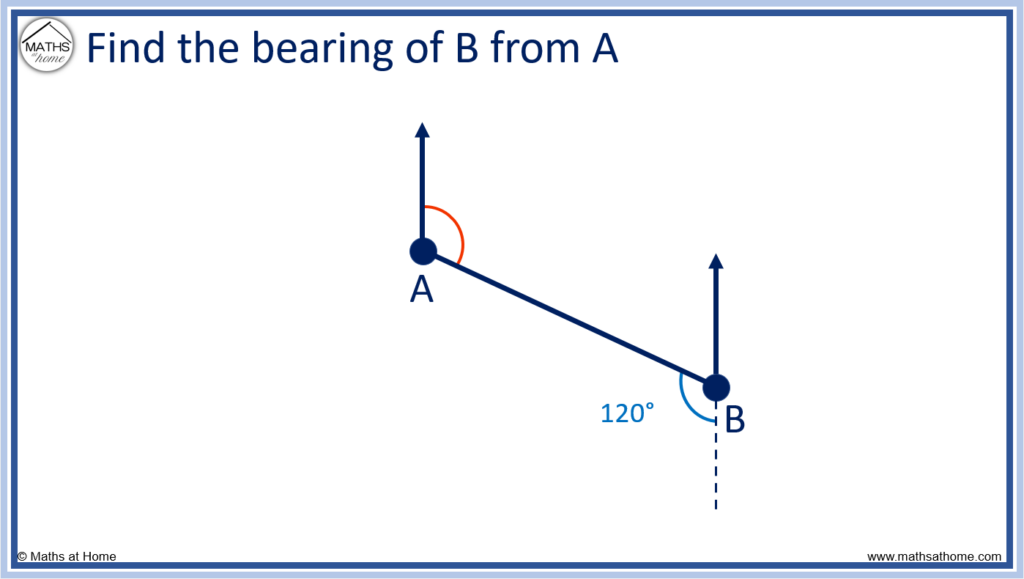
For example, find the bearing of B from A.
The angle of 120° is shown. It makes an alternate angle with the bearing of B from A.
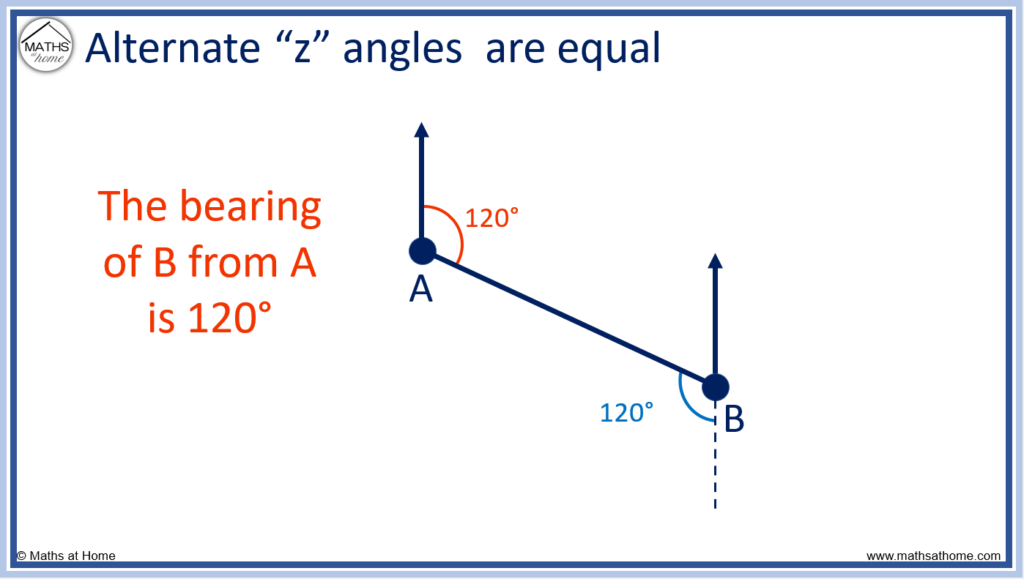
Therefore the bearing of B from A is also 120°.
Here is another example of using alternate angle facts to find a bearing.
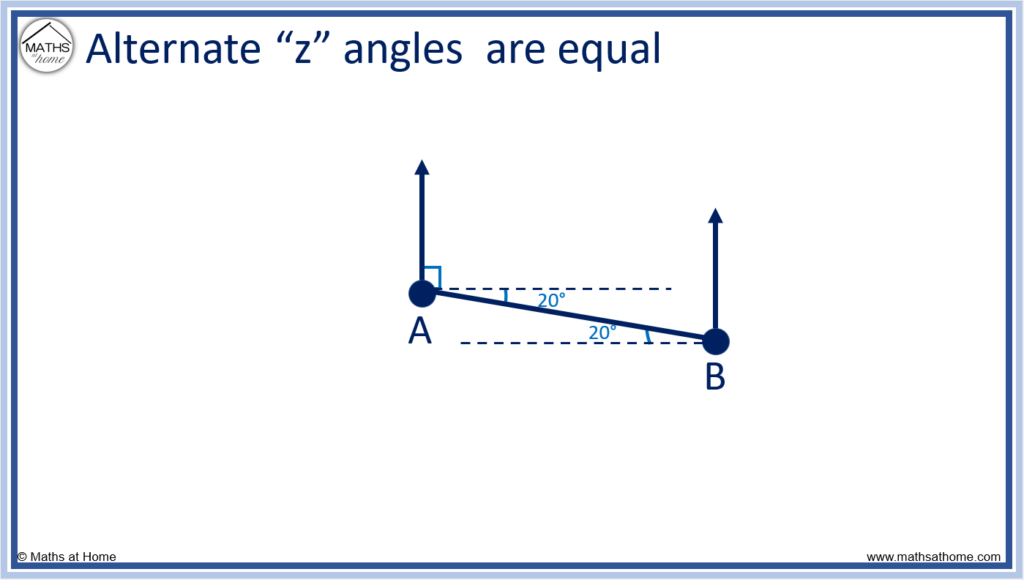
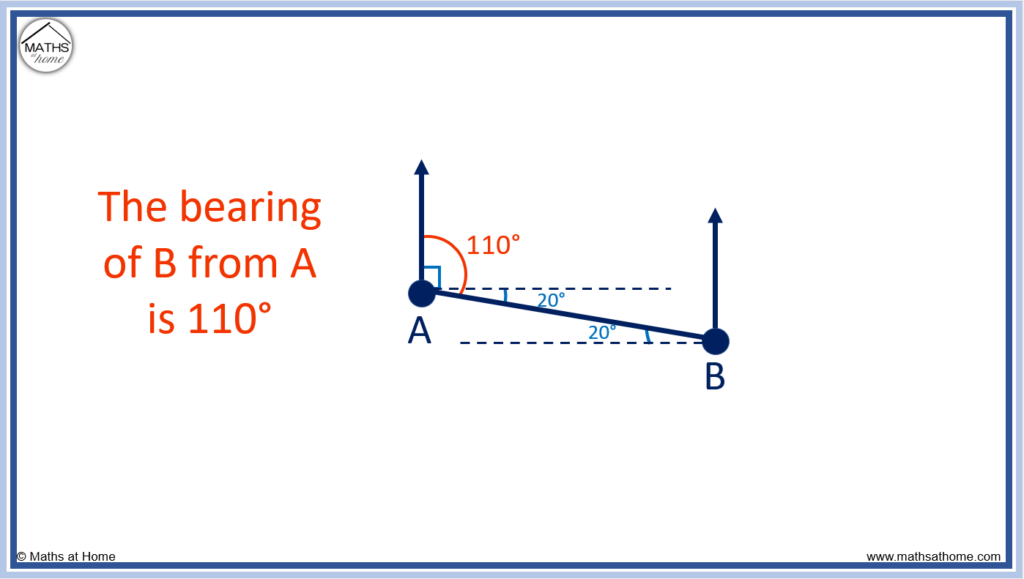
Find the bearing of B from A
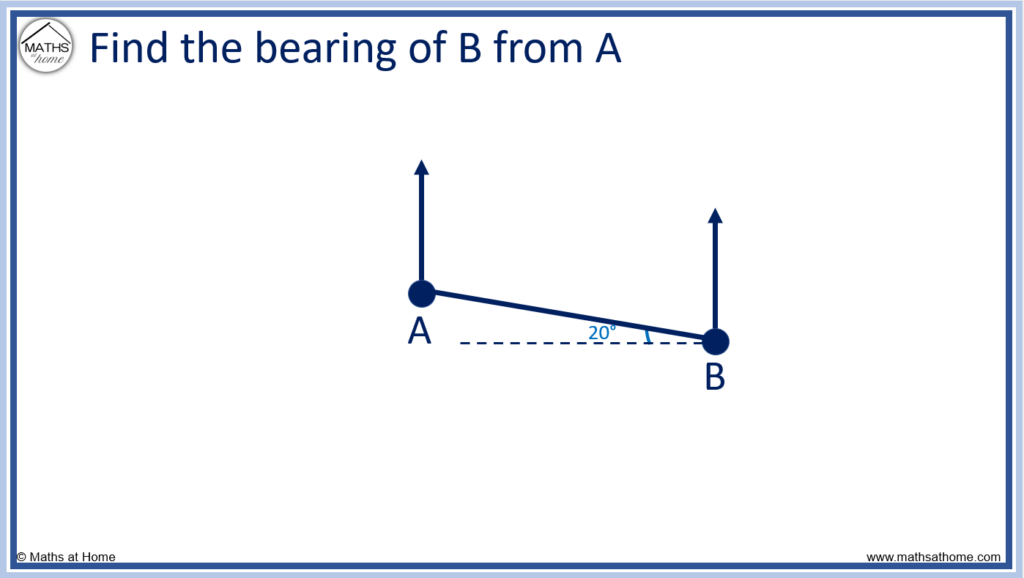
We can see that alternate angles are equal. Therefore the angle between the line AB and the horizontal is 20° as shown below.
The horizontal is 90° with north and so the bearing is 90° + 20° = 110° as shown.
How to Calculate a Bearing using Trigonometry
To find a bearing using trigonometry, create a right-angled triangle. If distances are given in any of the compass directions, label these sides as the adjacent or opposite sides of the triangle. If a distance is given in a particular bearing, label this distance as the hypotenuse of the triangle.
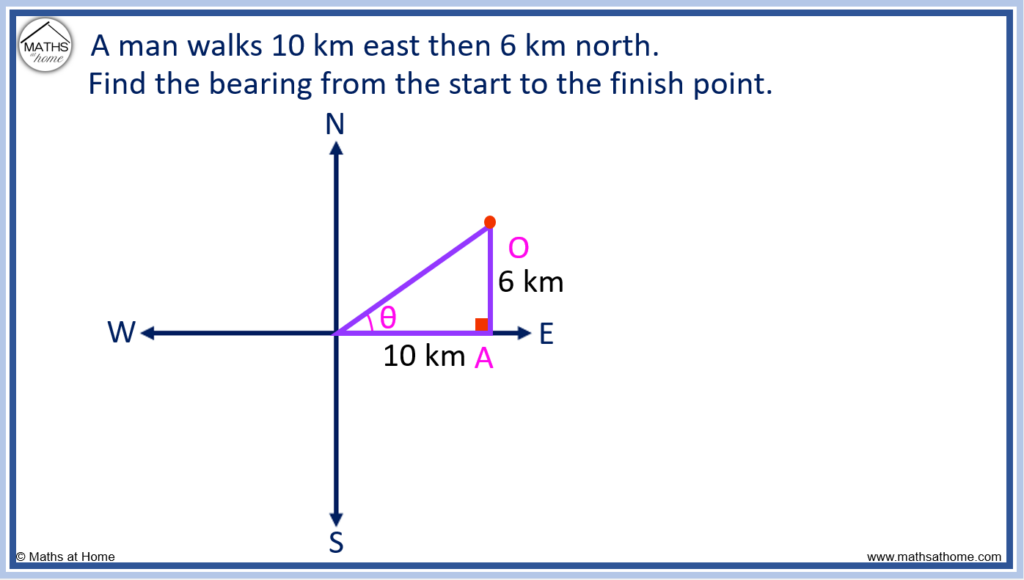
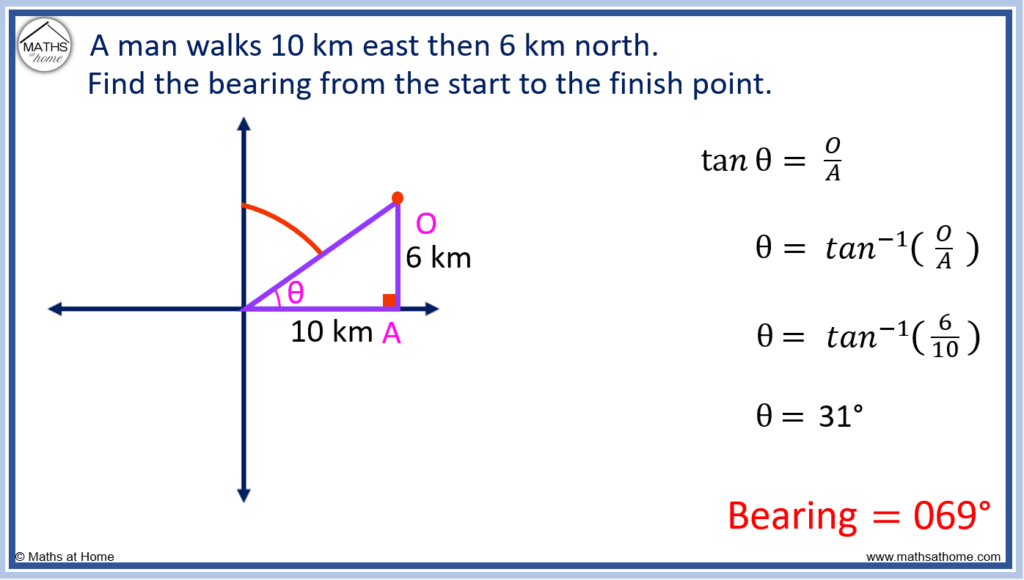
For example, a man walks 10 km east and then 6 km north. Find the bearing from the start to the finish point.
Since the distances given are in compass directions of east and north, a right-angled triangle can be drawn in which the 10 km east is the adjacent side and the 6 km north is the opposite side.
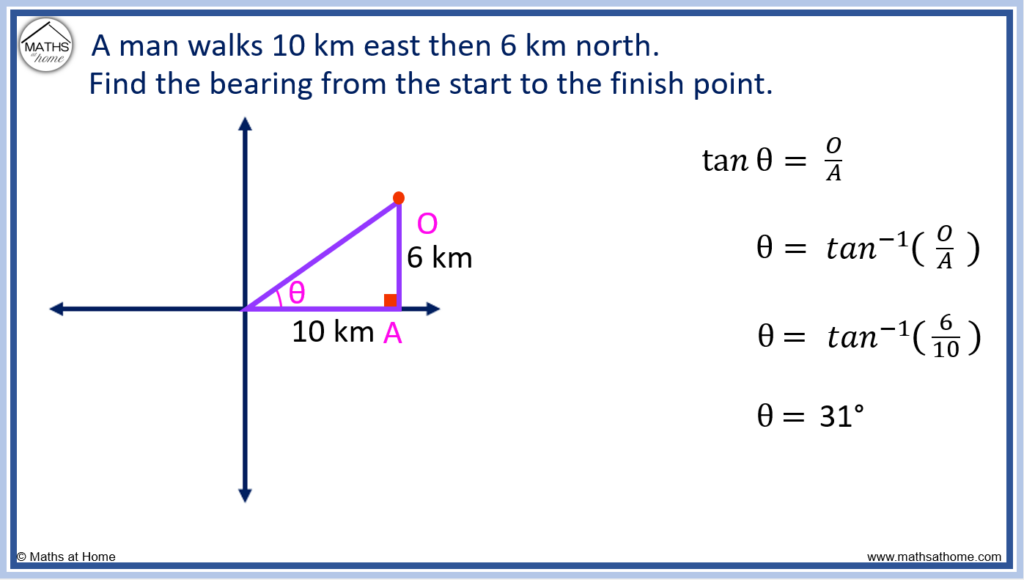
Since the two known sides of the triangle are the opposite and adjacent, we can use the tan function to find the angle shown.
and so,
.
Solving this, and so,
.
The bearing of the final position from the starting position must be given as clockwise from north. The bearing is indicated with the angle shown below.
To find this bearing, we know that the bearing plus make a total of 90°. We subtract 31° from 90° to get a bearing of 69°.
Here is another example of finding a bearing using trigonometry.
A boat sails 8 km west and then 3 km south. Find the bearing from the start to the finish point.
Since the distances given are in the compass directions of west and south, a right-angled triangle can be formed with an adjacent of 8 km and an opposite of 3 km.
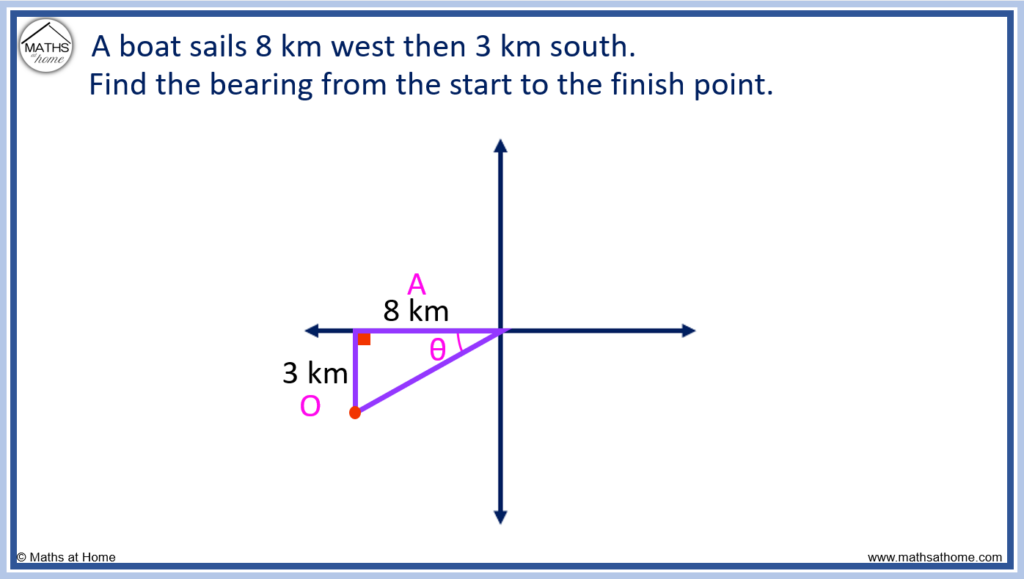
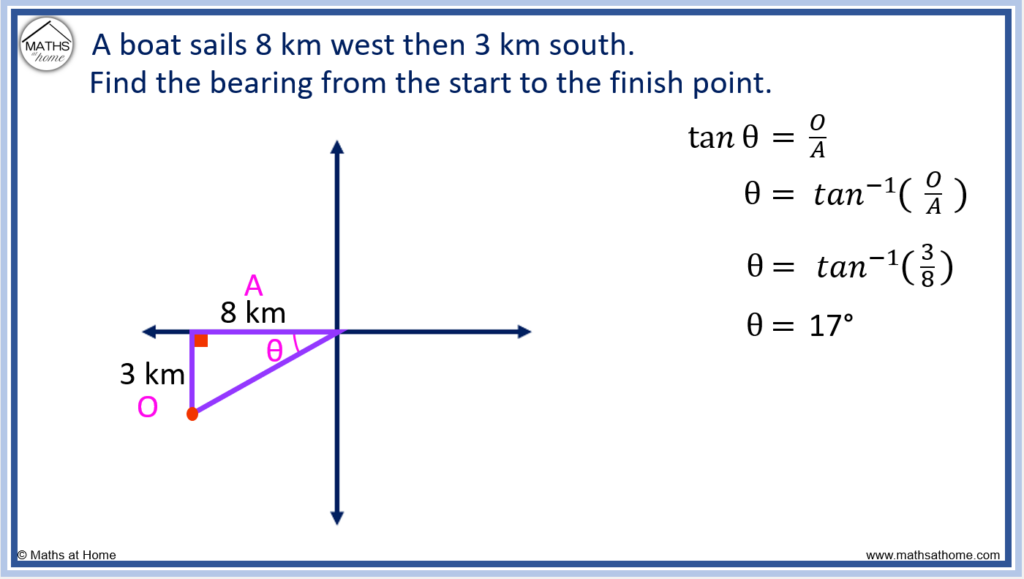
Since the known sides are the adjacent and the opposite, use .
Therefore and so,
.
.
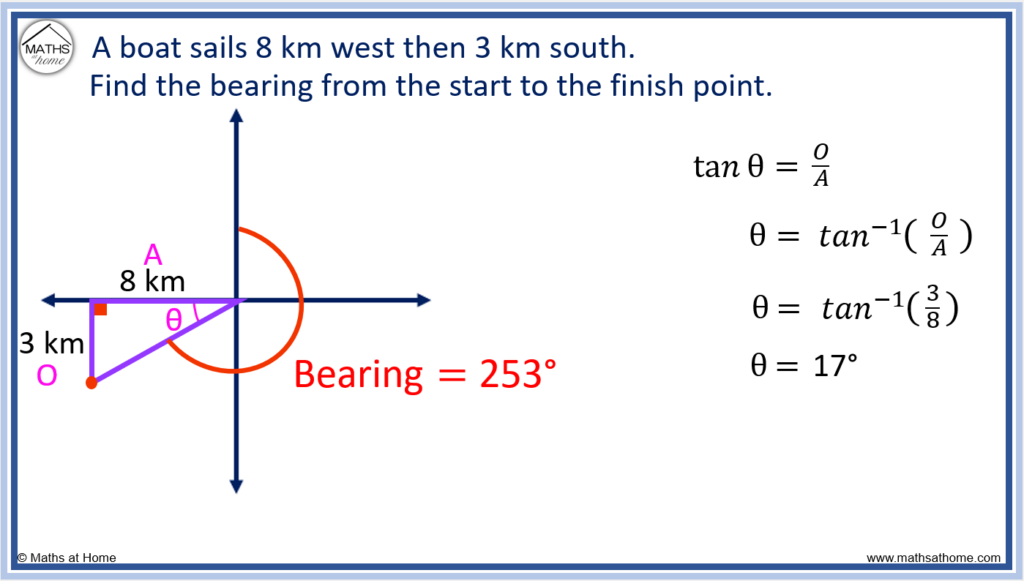
The bearing is always measured clockwise from north.
The bearing is the angle clockwise from north to west subtract θ.
From north to west is 270° and so the bearing is 270° – 17° = 253°.
Here is an example of how to find a distance when given a bearing.
A place travels 500 km on a bearing of 300°. How far west did the plane travel?
Start by drawing a diagram. 300° clockwise from north is shown below. It is past 270° but less than 360° and so, it lies between west and north.
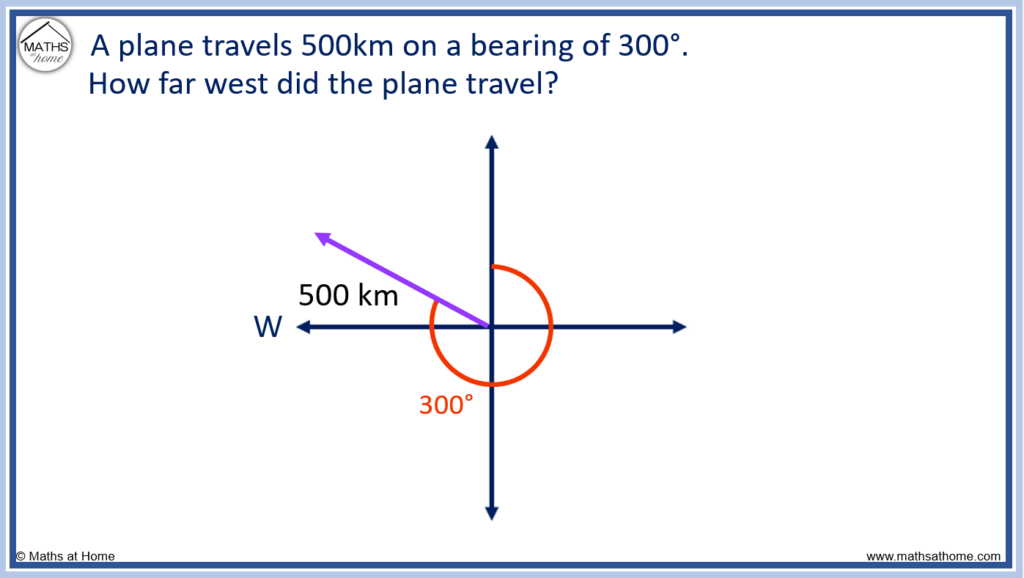
We draw a right-angled triangle with one of the sides indicating the distance travelled west.
The angle of the right-angled triangle must be 60° since 360° – 300° = 60°.
With the angle labelled as shown, the distance travelled west is the opposite side and 500 km is the hypotenuse.
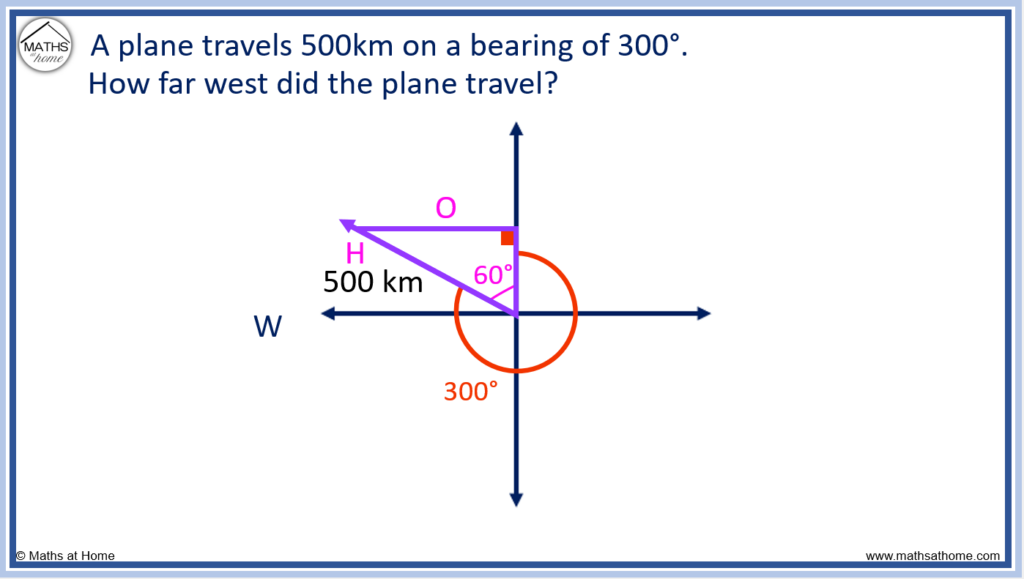
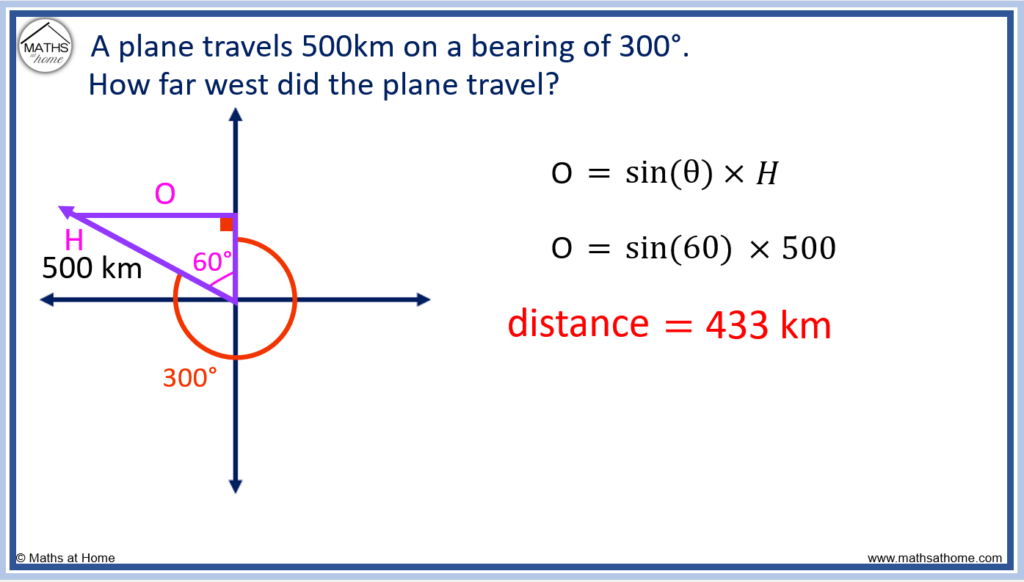
We require the distance travelled west, which is the opposite. We have the hypotenuse and the angle, θ = 60°.
Therefore we use .
Hypotenuse = 500 and θ = 60°
Therefore the .
The distance travelled west is therefore 433 km.
Bearings Using the Sine and Cosine Rule: Example 1
If bearings are made between three locations and a non-right-angled triangle is formed between them, then the sine rule or cosine rule, c2=a2+b2-2ab.cos(C) may be used to solve the problem. The distances travelled make up the side lengths a, b and c and the internal angles of the triangle are A, B and C.
In this example, the cosine rule is used to find a missing side length and then the sine rule is used to find a missing angle. This angle is then used to find the bearing.
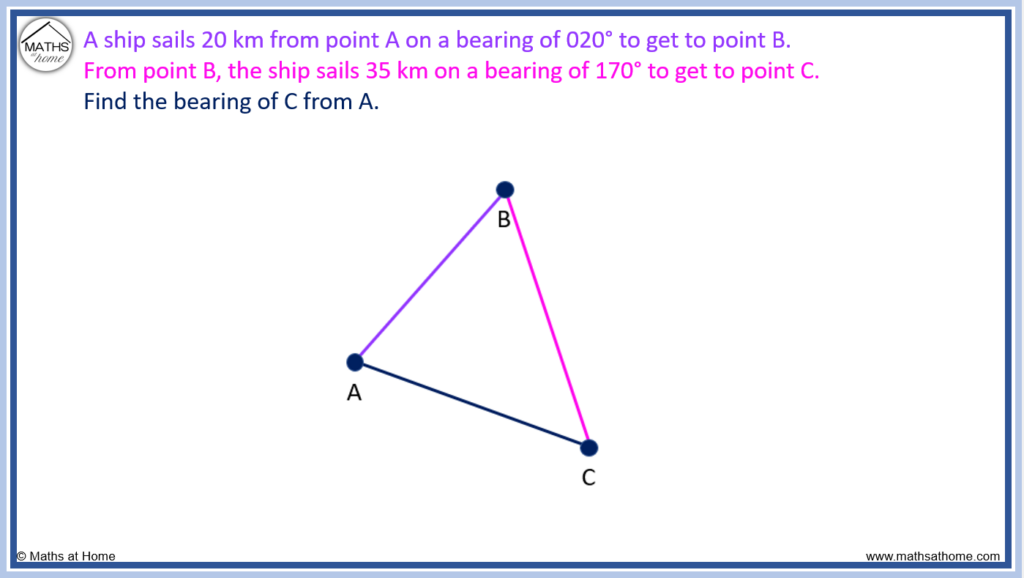
Step 1 below shows the diagram of the situation with bearings marked.
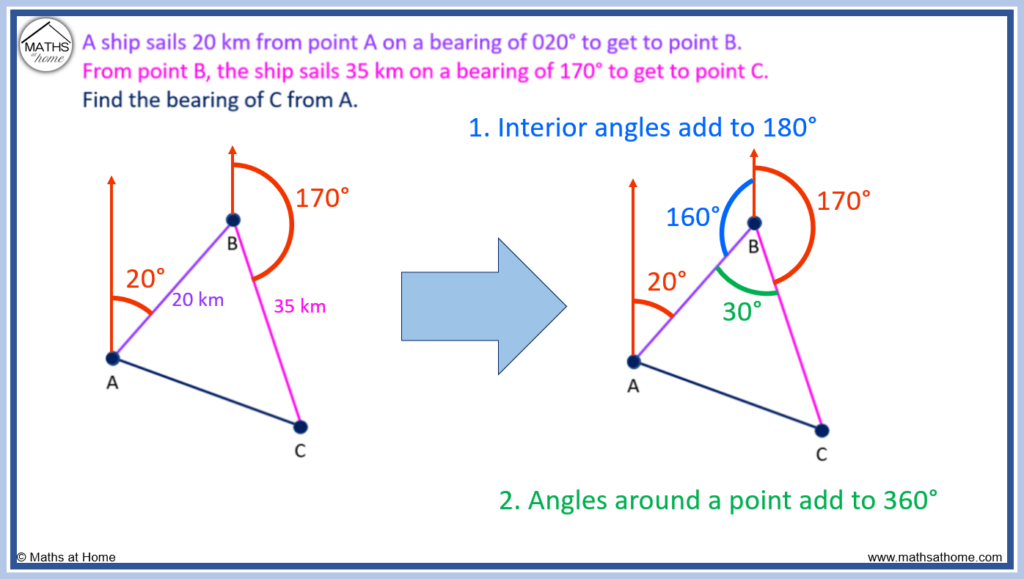
In Step 2, an interior angle of the triangle is found. Firstly, we use the fact that interior angles add to 180° to find the 160° angle marked in blue. Secondly, angles around a point add to 360°, so subtracting 160° and 170° from 360°, we see that the internal angle of the triangle must be 30°.
Step 1. Label a diagram with the bearings and lengths
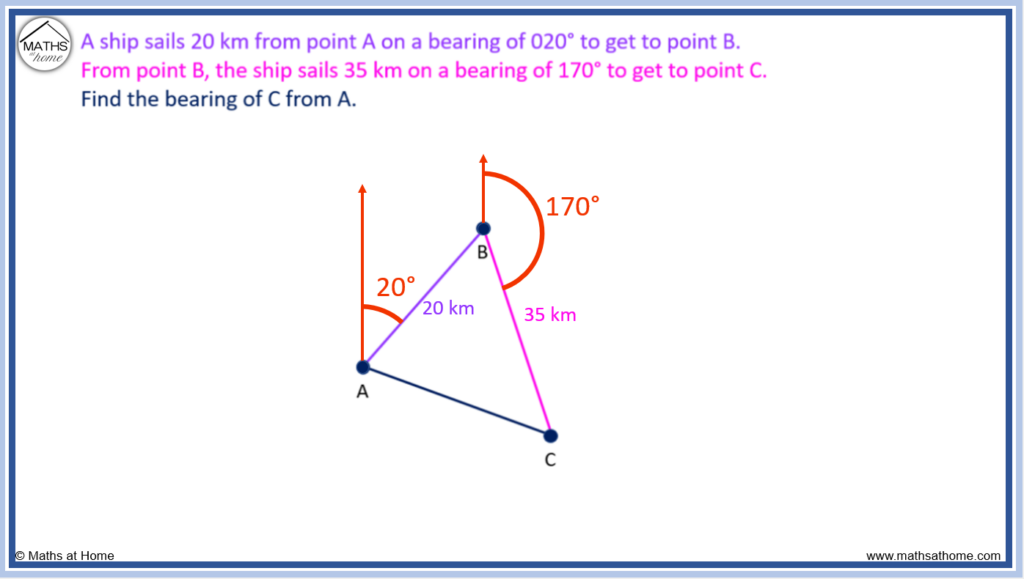
Step 2. Find any missing angles inside the triangle
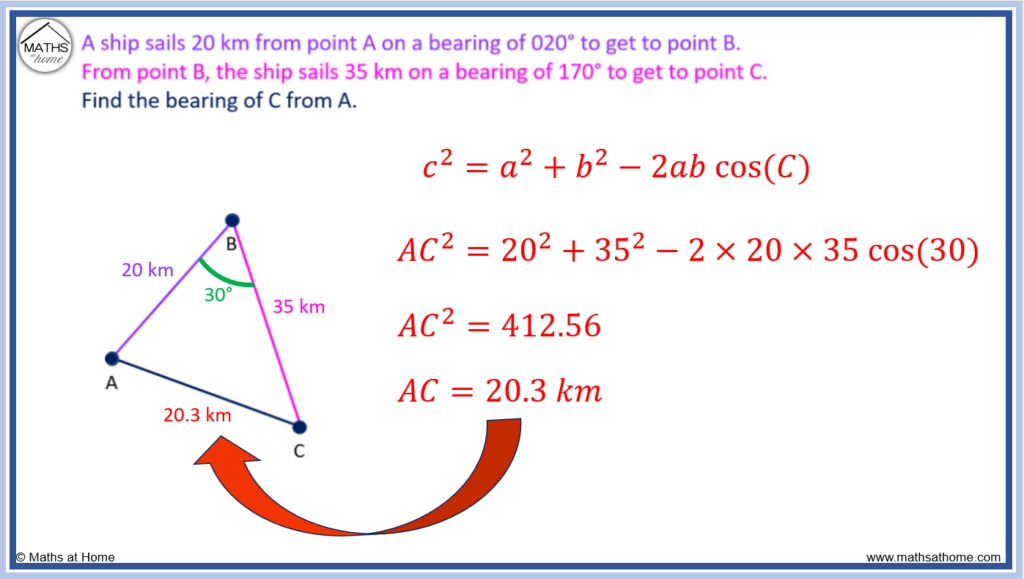
Step 3. Use the cosine rule to find the missing side opposite the known angle
The cosine rule can be used to find a missing side, c using the formula .
Here c is the missing side from A to C. Therefore C is the angle opposite, which is 30°.
a and b are the two other known side lengths, 20 and 35.
Substituting these values into the cosine rule, we get AC = 20.3 km.
Step 4. Use the sine rule to find a missing angle
The sine rule states that , which can be rearranged as
.
When using the sine rule, side a must be opposite angle A and side b must be opposite angle B.
We choose b and B as a pair of an opposite side and angle that we know.
a is the side opposite to the angle we wish to find.
Therefore a = 35, b = 20.3 and B = 30°.
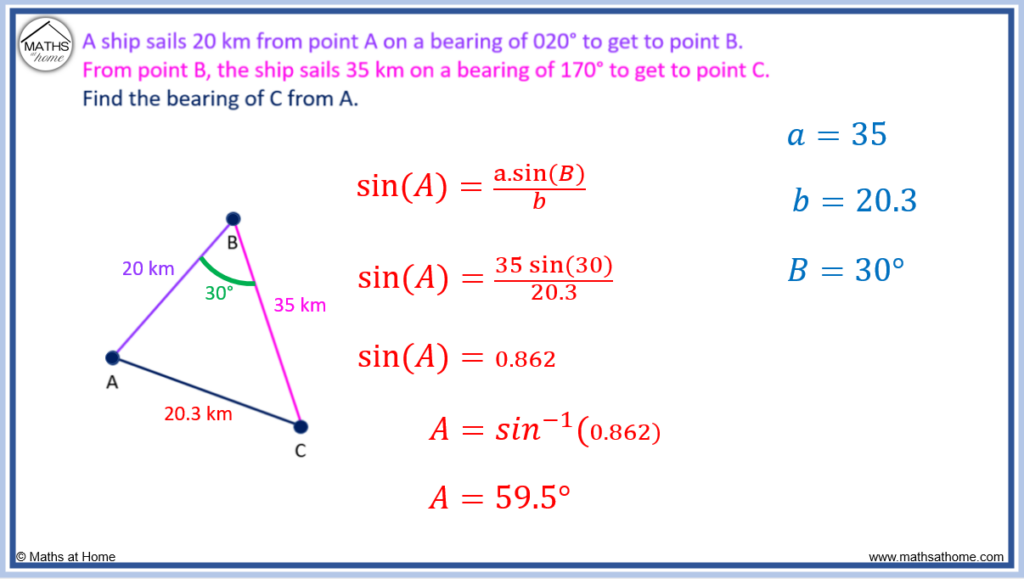
Therefore, .
Therefore, and so,
.
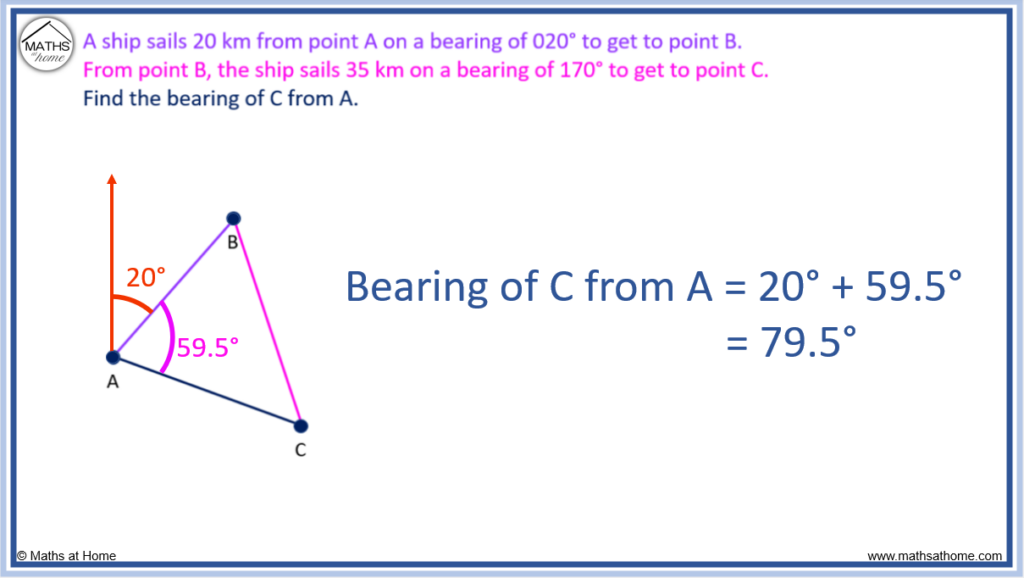
Step 5. Find the bearing as an angle clockwise from north
The bearing of C from A is found as the angle clockwise from north at A.
We can now combine the 20° bearing of A to B with the internal angle of the triangle 59.5°.
The bearing of A to C is 79.5°.
Bearings using the Sine and Cosine Rule: Example 2
A ship leaves point A on a bearing of 45° and travels for 13 km. Another ship leaves point A on a bearing of 155° and travels for 20 km. How far apart are the two ships?
In this example, a diagram is drawn and a non-right-angled triangle is created.
The internal angle of the triangle is found by the difference between the bearings. 155° – 45° = 110°.

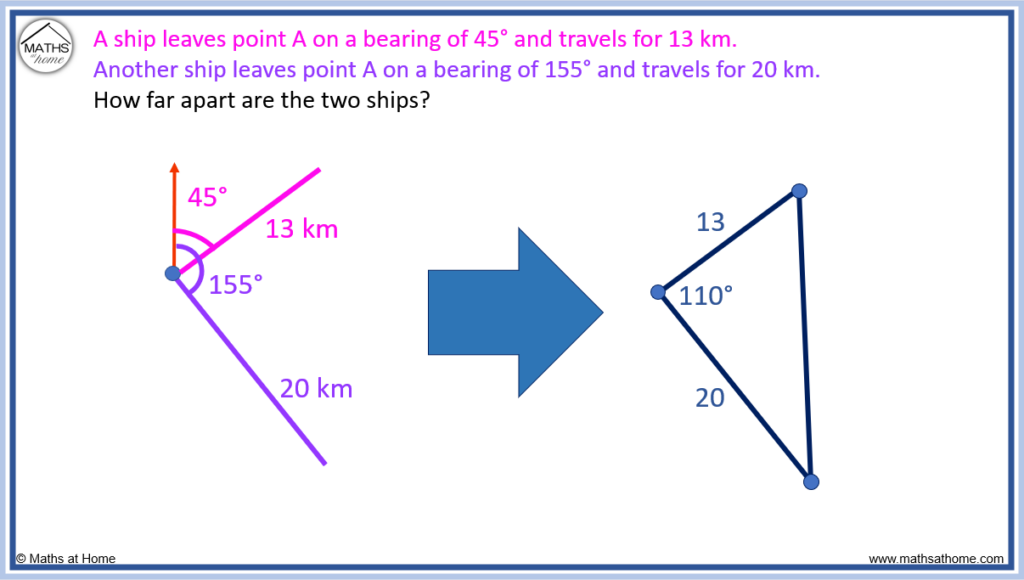
The cosine rule can be used to find the distance between the two ships, shown by the right hand side of the triangle.
The missing side is labelled as c and the cosine rule is .
a and b are the two known sides either side of the angle C.
a = 13, b = 20 and C = 110°.

becomes
.
Therefore and so, the missing side c = 27.3 km.
Bearings with Vectors
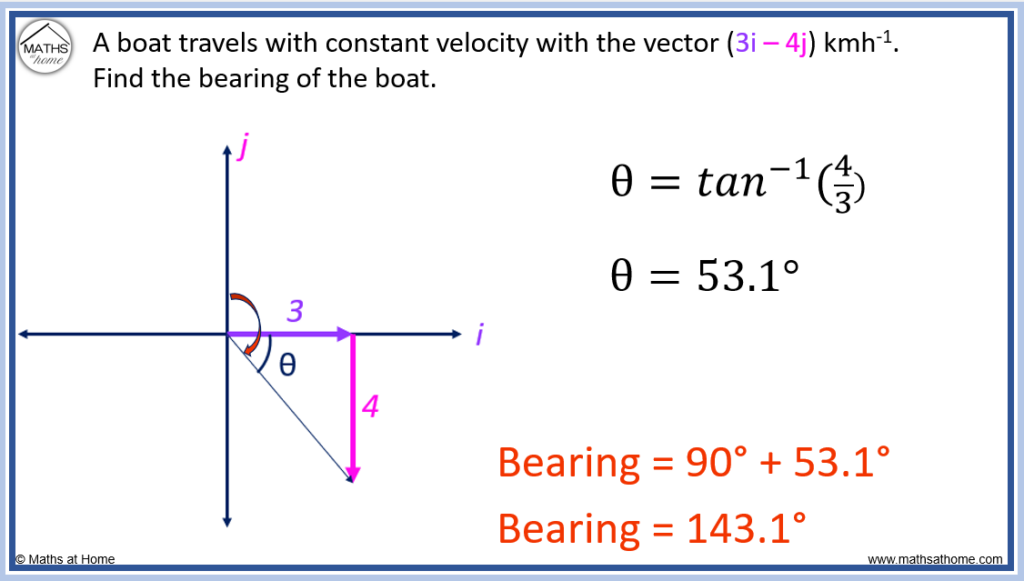
For any vector of the form ai+bj, the angle of the vector is found using tan-1(b/a). The bearing of the vector is then found as the angle clockwise from north. For example, the vector (3i-4j) makes an angle of tan-1(4/3) = 53° below east. The bearing is found as 90°+53°=143°.
Vectors can be written as bearings since:
A positive i component is in the eastern direction.
A negative i component is in the western direction.
A positive j component is in the northern direction.
A negative j component is in the southern direction.
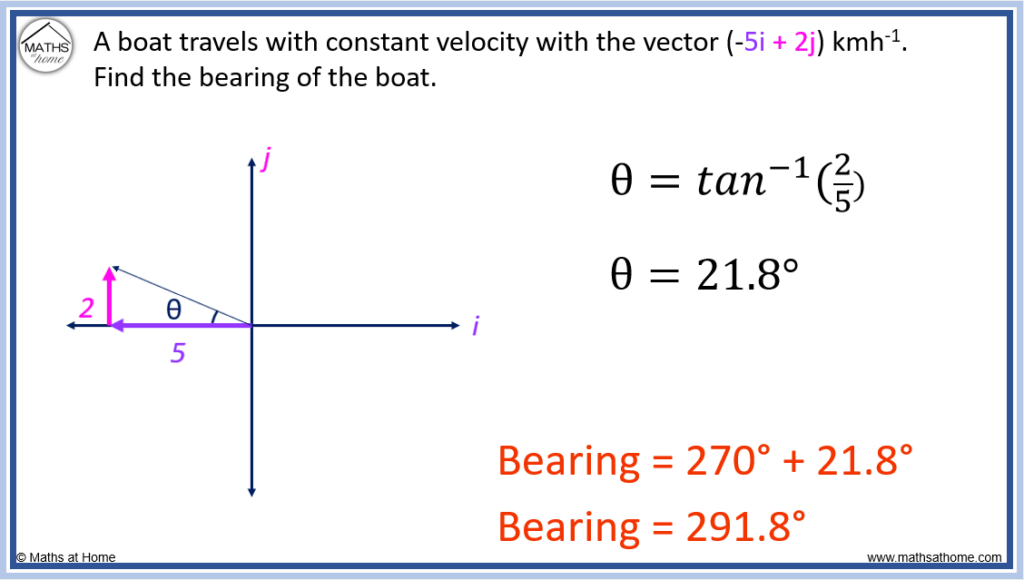
For example, a boat travels with a constant velocity with the vector (-5i+2j) kmh-1. Find the bearing of the boat.
-5i is in the westerly direction and 2j is northerly.
The angle from the horizontal is found as . Therefore
.
The west direction is at a bearing of 270° and so, the bearing of the boat is 270° + 21.8° = 291.8°.
As a three-figure bearing, this is 292°.