Simpson’s Rule for Area of a Shape: Video Lesson
Simpson’s 1/3 Rule For Area Formula
Simpson’s rule for finding the area of a shape is: Area=(w/3)×[yfirst + 4(yodd) + 2(yeven) + ylast], where w is the equal width between each measurement, yfirst and ylast are the first and last measurements, yodd is the sum of the odd measurements and yeven is the sum of the even measurements.
The Simpson Rule Formula is used for calculating the approximate area of shapes with curved boundaries.
Simpson’s 1/3 Rule for Calculating Area
- w = the equal width of each subinterval (width between each measurement)
- yfirst = the first measurement
- yfirst = the last measurement
- yodd = the sum of the odd measurements
- ylast = the sum of the even measurements

Simpson’s rules are several different equations named after the mathematician Thomas Simpson which can be used for finding areas.
Whilst many other forms of Simpson’s rule involve integration, Simpson’s 1/3 Rule is a formula that does not involve integration and can be used to approximate the area of an irregular shape by taking equally-spaced measurements of the height of the shape.
Simpson’s 1/3 rule (also known as Composite Simpson’s rule) involves a quadratic interpolation of a parabola between the points given and is more accurate than the trapezoidal rule for area. Alternate formulae can be used for Simpson’s rule involving definite integrals.
The area of the shape is broken into ‘n‘ equally-sized strips of width ‘w’. These are sometimes known as the subintervals.
To improve the accuracy of the Simpson’s Rule approximation, a greater number of measurements should be taken. Essentially, a larger n value (or smaller strip width) leads to a more accurate result.
Limitations with Simpson’s rule include:
- The need to have equally-spaced measurements, which may not always be possible.
- Several measurements may be needed to sufficient accuracy, which may not always be possible.
- Poor accuracy when considering shapes with sharp corners or rapid changes in measurements.
How to Calculate the Area of a Shape Using Simpson’s Rule
To calculate the area of a shape using Simpson’s rule use the formula Area=(w/3)[yfirst + 4(yodd) + 2(yeven) + ylast], where w is the width between each measurement, yfirst and ylast are the first and last meaurements, yodd is the sum of the odd measurements and yeven is the sum of the even measurements.
For example, calculate the area of the irregular shape shown below with measurements taken every 6 metres:
Here, w = 6 m.
- yfirst = 5 m
- y1 = 25 m
- y2 = 26 m
- y3 = 18 m
- y4 = 20 m
- y5 = 16 m
- y6 = 12 m
- ylast = 2 m
Therefore: and so,
.
and so,
.
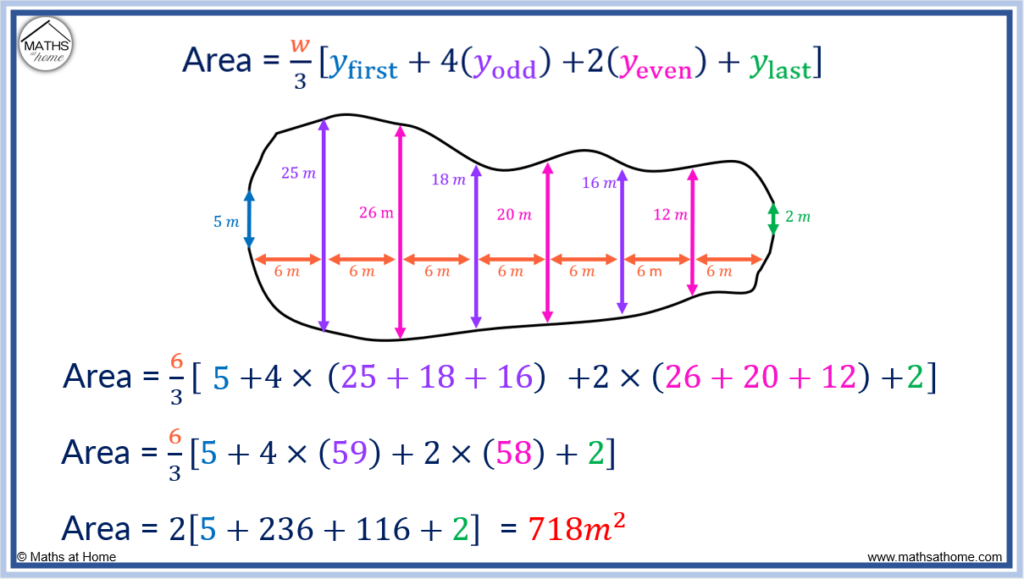
The Simpson’s rule of becomes:
Evaluating this, we obtain: which simplifies to
and so,
.
Therefore the approximate area of the irregular shape is 718 m2.
Simpson’s Rule Examples: Questions and Answers
Here are some further examples of using Simpson’s one-third rule to calculate the area of irregular shapes.
For example, the length of a curved island is measured in subintervals every 20 m as shown in the diagram. Approximate the area.
In this example, the first (yfirst) and last (ylast) measurements are 0 m as represented by the dots on each end of the diagram below.
Since the measurements are taken every 20 metres, the value of w = 20.
- yfirst = 0
- y1 = 30
- y2 = 40
- y3 = 50
- y4 = 60
- y5 = 22
- ylast = 0
Therefore and so,
.
and so,
.

The Simpson’s rule of becomes:
which simplifies to
.
can be evaluated by multiplying 20 by 608 and dividing by 3 to obtain
.
Here is another example of using Simpson’s 1/3 rule to find the area of a shape.
The distance across a swimming pool is measured every 150 cm as shown in the diagram. Approximate the area.
Since the distances are measured every 150 cm, the value of w = 150.
The first measurement is zero as represented by the dot at the start of the diagram below. Therefore yfirst = 0.
- yfirst = 0
- y1 = 180
- y2 = 240
- y3 = 320
- ylast = 350
Therefore and so,
.
.

The Simpson’s rule of becomes:
.
This simplifies to which becomes
and so,
.
This is equivalent to an area of 14.15 m2.
Simpson’s Rule From a Table
Simpsons rule, Area=(w/3)[yfirst + 4(yodd) + 2(yeven) + ylast] can be used to calculate the area of a shape when the values are given in a table. yfirst is the first value in the table, ylast is the last value in the table. yodd is the sum of the values in the odd rows of the table and yeven is the sum of the even rows of the table.
For example, use Simpson’s rule to calculate the area of the shape with measurements taken every 9 cm as given in the following table:
| yfirst | 6 cm |
| y1 | 3 cm |
| y2 | 7 cm |
| y3 | 9 cm |
| y4 | 5 cm |
| y5 | 4 cm |
| y6 | 8 cm |
| ylast | 0 cm |
and so,
.
and so,
.

The Simpson’s rule area formula of becomes
.
This simplifies as or
.
Therefore the area of the shape is 330 cm2.
Using Simpson’s Rule in Surveying
Simpson’s rule is a numerical method for approximating irregularly shaped areas. In surveying, Simpson’s rule can be used to approximate the area of plots of land by dividing the land into an even number of equally-sized intervals and measuring the height at each interval.
Here are the steps for using Simpson’s rule in surveying:
- Divide the land into ‘n‘ equally-spaced intervals along the x-axis and record the width between them as ‘w‘
- Measure the height (elevation) of the land at each of the intervals, f(xi).
- Use Simpson’s rule: Area ≈ (w/3) [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + … + 2f(xn-2) + 4f(xn-1) + f(xn)]
The number of ordinates is the number of measurements made. In this example, we have 6 ordinates.
We multiply the odd ordinates by 4 and the even ordinates by 2. The first and last ordinates are not multiplied.
For example, the following elevations were measured along the curve every 30 m (so ‘w’ = 30)
- f(x0) = 15
- f(x1) = 18
- f(x2) = 24
- f(x3) = 31 – this is f(xn-2)
- f(x4) = 32 – this is f(xn-1)
- f(x5) = 35 – this is f(xn)
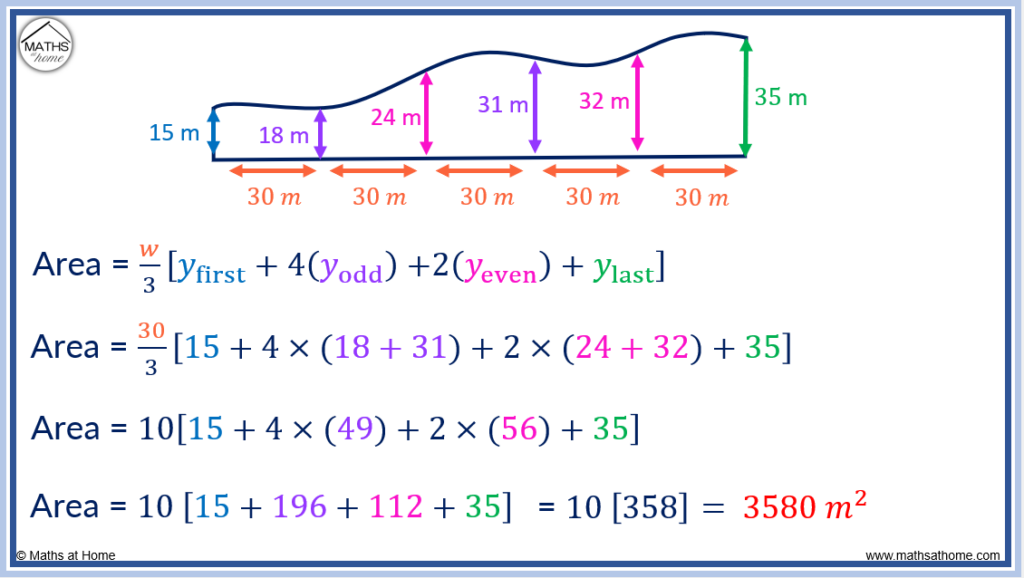
Therefore, Area ≈ (w/3) [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + … + 2f(xn-2) + 4f(xn-1) + f(xn)] becomes:
Area ≈ (30/3) [15 + 4×18 + 2×24 + 4×31 + 2×32 +35] ≈ 3580 m2
Therefore the cross area of the surveyed land is approximately 3580 m2.
