Scientific Notation: Video Lesson
What is Scientific Notation?
Scientific notation can be used to represent both decimals less than one whole and very large whole numbers.
Scientific notation is a concise way to represent both very large or very small numbers. Scientific notation involves a number between 1 and 10 being multiplied to a power of 10. The power of 10 is positive if the number being represented is large and it is negative if the number is small.
- A positive power of 10 tells us how many digits the number has between its first digit and the decimal point
- A negative power of 10 tells us how many zero digits are in front of the non-zero digits.
For example, 6×105 is a 6 followed by 5 digits. It represents 600 000.
For example, 6×10-5 is a 6 with 5 zeros before it. It represents 0.00006.

How Scientific Notation is Used in Real Life
Scientific notation is used whenever very large or very small numbers are involved. For example in physics, astronomy, chemistry and finance.
Some examples of scientific notation used in real-life include:
- The very large distances involved in astronomy. For example, the distance between the Earth and the Sun is said to be 93 million miles, which can be written as 9.3 × 107 miles.
- In Physics, very large or very small known constants are represented in scientific notation such as the speed of light (2.998 × 108 meters per second) or Planck’s constant (6.63 × 10-34 joule-seconds).
- In chemistry, the mass of atoms, molecules and molar mass is often written in scientific notation. For example, Avogadro’s number is 6.02 × 1023 particles per mole.
- In finance and economics, figures such as national debt, gross domestic product (GDP), or market capitalisation are often expressed in scientific notation. For instance, if a country’s GDP is $2.5 trillion, it would be expressed as 2.5 × 1012 dollars.
- Engineers often work with values that span many orders of magnitude, such as voltage, current, or power.
- In medicine and biology, scientific notation is used to express values like cell counts, DNA base pairs, or concentrations of substances in body fluids.
In science, abbreviations are commonly used to refer to given orders of magnitude such as:
| Order of Magnitude | Scientific Notation |
| femto | ×10-15 |
| pico | ×10-12 |
| nano | ×10-9 |
| micro | ×10-6 |
| milli | ×10-3 |
| centi | ×10-2 |
| deci | ×10-1 |
| deca | ×101 |
| hecto | ×102 |
| kilo | ×103 |
| mega | ×106 |
| giga | ×109 |
| tera | ×1012 |
| peta | ×1015 |
Here are some common values of scientific notation listed on a number line from least to greatest.

Scientific Notation Explained
Scientific notation is used when a very large or very small number is too long to write in the normal manner. In scientific notation numbers are written as a number between 1 and 10 multiplied by a power of 10. For example, 32500 is written as 3.25×104.
Scientific notation is a more concise way to write long numbers whilst indicating their order of magnitude.
Scientific notation is also commonly known as standard form. Both scientific notation and standard form refer to numbers written as a number between 1 and 10 multiplied by 10 to the power of some other positive or negative number.
For example consider the following lists:
- 101 = 10
- 102 = 100
- 103 = 1000
- 104 = 10000
The power that 10 is raised to in each case is equal to the number of digits after the 1.
- 3 × 101 = 30
- 3 × 102 = 300
- 3 × 103 = 3000
- 3 × 104 = 30000
The power that 10 is raised to in each case is equal to the number of digits after the 3.

A number written in scientific notation always consists of the following parts:
- A number between the values of 1 and 10
- A multiplication by 10 raised to a power

The name for a number not written in scientific notation is simply ‘standard notation’ or ‘decimal notation’. When comparing a number written in standard notation to a number written in scientific notation, it may also be referred to as ‘expanded form’.
The first step is to write the first part of the number which must always be between 1 and 10.
We take 32500 and write it as 3.25 so that it is now a number that is bigger than 1 and less than 10.
The next step is to find the power of 10 that 3.25 is raised to to make it equal to 32500.
The power that ten is raised to is equal to the number of digits after the first digit.
In 32500, there are 4 digits after the first digit of 3. Therefore the power that 10 is raised to is 4.
32500 can be written as 3.25 × 104.
Scientific notation is often used on calculator displays (since the calculator screen cannot fit very long numbers). On a calculator, scientifi notation is written using ‘E’ to represent ×10^.
For example, 32500 can be written as 3.25 × 104 or alternatively as 3.25E4.
In scientific notation, E stands for ×10 raised to the power of the number that comes after the E.

Scientific notation can also be used to write very small numbers by using negative powers of 10.
10-1 means or 0.1
10-2 means or
or 0.01.
We can see that the negative power of 10 describes how many zeros are at the start of the decimal number.
For example, 10-3 has 3 zeros when written as 0.001.

The number 0.000034 can be written as 3.4 × 10-5. There are 5 zeros before the digits of 3 and 4.
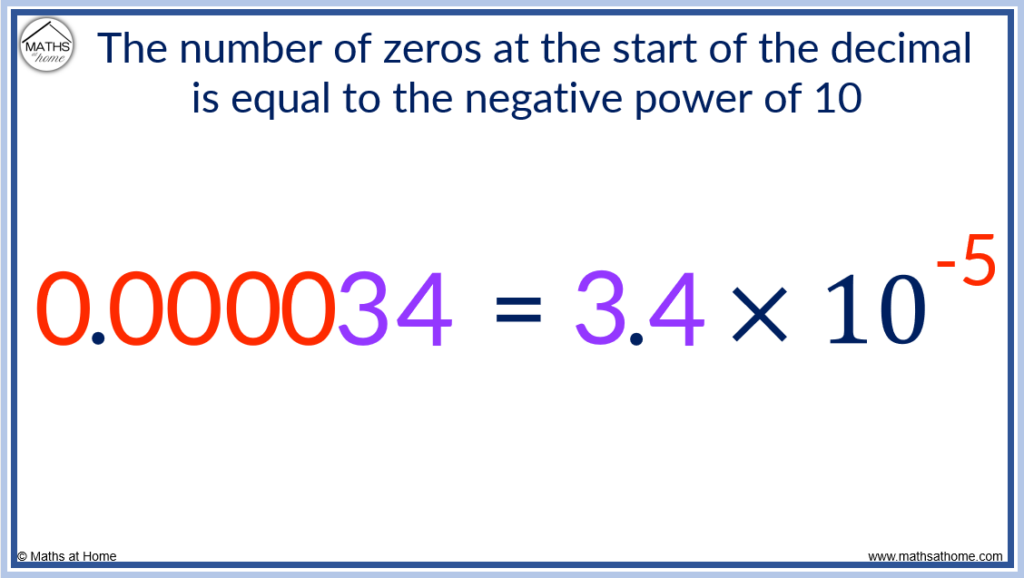
Rules of Scientific Notation
Numbers written in scientific notation must adhere to the following rules:
- The number before the multiplication sign must always be at least 1 and less than 10.
- There is always a multiplication by a power of 10 (as opposed to a multiplication by any other number).
- The power of 10 can be negative, zero or positive.
- If the number being represented is 10 or more, the power of 10 is positive.
- If the number being represented is 10 or more, the power of 10 is equal to the number of digits that come after the first digit of the number.
- If the number being represented is less than 1, the power of 10 is negative.
- If the number being represented is less than 1, the power of 10 is equal to (-1) multiplied by the number of zeros at the start of the number.
- If the number being represented is greater than 1 but less than 10, the power of 10 is zero.
How to Write Large Numbers in Scientific Notation
To write a large number in scientific notation:- Write a decimal point after the first digit of the number to form a number between 1 and 10.
- Multiply this by a power of 10, where the power is equal to the number of digits after the first digit of the large number.
For example, write 630000 in scientific notation:
Step 1. Write a decimal point after the first digit of the number to form a number between 1 and 10
A decimal point is placed after the 6 to make 6.30000 which is just 6.3
6.3 is a number between 1 and 10.
Step 2. Multiply this by a power of 10, where the power is equal to the number of digits after the first digit of the large number
The first digit of 630000 is 6. We count the number of digits after this first digit of 6.
There are 5 digits after the first digit. That is, the 3, 0, 0, 0 and 0.
Therefore we multiply by 105.
630000 is written in scientific notation as 6.3×105.

How to Write Small Numbers in Scientific Notation
To write small numbers in scientific notation:
- Write the non-zero digits as a number between 1 and 10.
- Multiply this by a negative power of 10 equal to the number of zeros in front of the first non-zero digit.
For example, write 0.000008 in scientific notation.
Step 1. Write the non-zero digits as a number between 1 and 10
The zeros at the start of 0.000008 are ignored to obtain the non-zero digit of 8.
8 is written because it is a number between 1 and 10.
Step 2. Multiply this by a negative power of 10 equal to the number of zeros in front of the first non-zero digit
The first non-zero digit in 0.000008 is the 8.
The number of zeros in front of this non-zero digit is 6.
Since there are 6 zeros, we multiply the 8 by 10 to the power of -6.
0.000008 is written in scientific notation as 8×10-6.

Small numbers less than one whole are written in scientific notation with a negative exponent representing the number of zeros at the start of the number.
For example, write the number 0.0257 in scientific notation.
Step 1. Write the non-zero digits as a number between 1 and 10
The zeros at the start of 0.0257 are ignored and the decimal point is placed after the first non-zero digit of 2.
This results in 2.57 which is a number between 1 and 10.
Step 2. Multiply this by a negative power of 10 equal to the number of zeros in front of the first non-zero digit
The first non-zero digit is 2.
There are 2 zeros before the 2 and so, we multiply 2.57 by 10 to the power of -2.
0.0257 is written in scientific notation as 2.57×10-2.
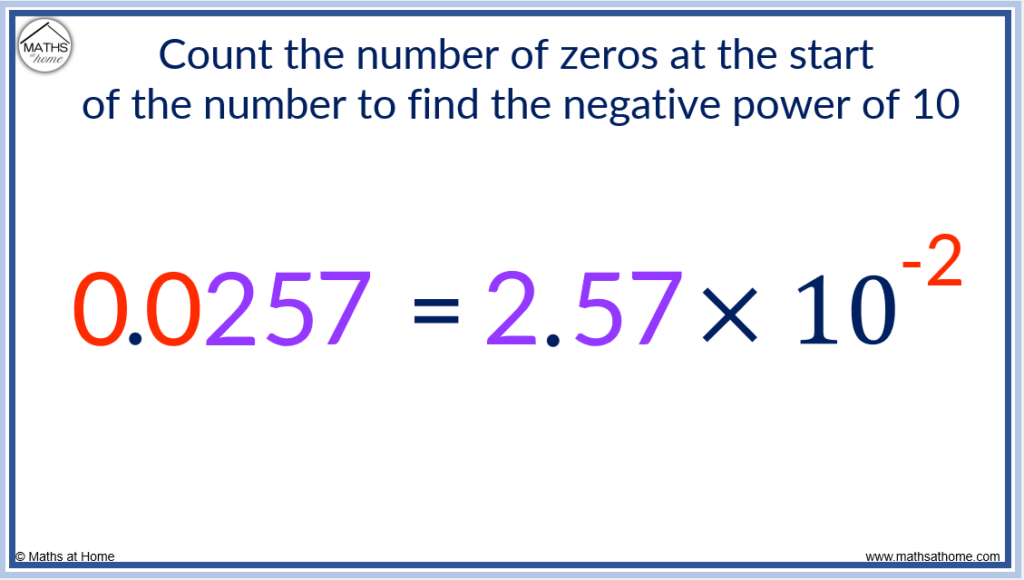
The power of the 10 is equal to the number of zeros at the start of the number multiplied by -1.
How to Read Scientific Notation
- If the power of 10 is positive, this is the number of digits after the first digit. So 2.11×106 has 6 digits after the 2. It is written as 2110000.
- If the power of 10 is negative, this is the number of zeros in front of the digits. So 5.3×10-3 has 3 zeros at the start. It is written as 0.0053.
Scientific Notation for a Large Number
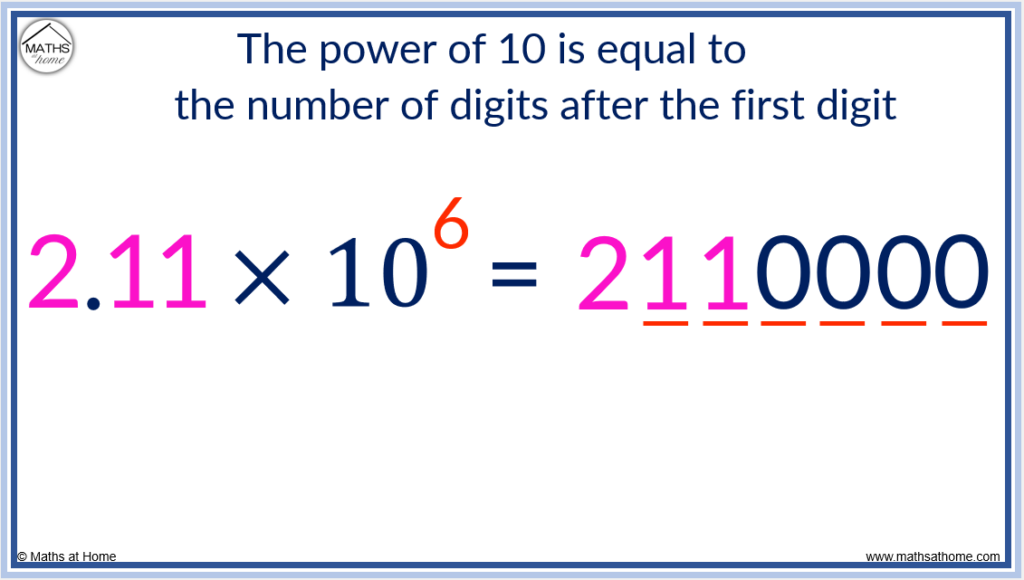
The power of 10 is 6 and so, there are 6 digits after the 2.
We already have two digits of 1 and so, four more 0 digits are needed.
Scientific Notation for a Small Number

The power of 10 is negative 3.
Negative powers tell us how many 0 digits are at the start of the number.
We put three 0 digits and then the 5 and the 3.
The decimal point always comes after the first 0 digit.
For example, 2.93 × 104 has 4 digits after the first digit of 2.
Following the 2, there is a 9 then a 3. We need two more 0 digits to obtain 4 digits after the 2.
2.93 × 104. = 29300.

For example, 1.04 × 10-4 has a negative power of 10.
Therefore this power is equivalent to the number of zeros at the start of the number. There will be 4 zeros followed by the digits of 1, 0 and 4.
1.04 × 10-4 = 0.000104.
Notice that the power of 10 is only equal to the number of zeros at the start of the number, not the total number of zeros in the answer.

Examples of Scientific Notation
Notice that as an extra zero digit is added to the value, the exponent in scientific notation increases by 1.
Notice that as we move from one thousand to one million to one billion to one trillion, three zero digits are added and so, the exponent in scientific notation increases by 3.
Here are some common values listed in scientific notation:
| Number | Standard Notation | Scientific Notation |
| One Thousandth | 0.001 | 1×10-3 |
| One Hundredth | 0.01 | 1×10-2 |
| One Tenth | 0.1 | 1×10-1 |
| One | 1 | 1×100 |
| Ten | 10 | 1×101 |
| One Hundred | 100 | 1×102 |
| One Thousand | 1 000 | 1×103 |
| Ten Thousand | 10 000 | 1×104 |
| One Hundred Thousand | 100 000 | 1×105 |
| One Million | 1 000 000 | 1×106 |
| One Billion | 1 000 000 000 | 1×109 |
| One Trillion | 1 000 000 000 000 | 1×1012 |
The power of zero in 1×100 means that zero tens have been multiplied by.
That is, 100 = 1 and so 1×100 simply means 1×1 which is just equal to 1.
Here are some examples of numbers written in scientific notation:
| Standard Notation | Scientific Notation |
| 0.0006 | 6×10-4 |
| 0.005 | 5×10-3 |
| 0.028 | 2.8×10-2 |
| 0.349 | 3.49×10-1 |
| 5.4 | 5.4×100 |
| 12.7 | 1.27×101 |
| 400 | 4×102 |
| 500 | 5×102 |
| 1230 | 1.23×103 |
| 54400000 | 5.44×107 |
How to Round Numbers in Scientific Notation
It is common for numbers to be written to a particular number of significant figures and then written in scientific notation. This is because numbers in scientific notation are very large or very small and so, the final digits do not really impact on the overall size of the number.
Typically, numbers in scientific notation are given to 2 or 3 decimal places although further accuracy may be required.
It is common to round numbers in scientific notation to 3 significant figures.
First round a number to the given significant figures and then convert this number to scientific notation.For example, write 125364 in scientific notation, rounded to 3 significant figures.
The first step is to round the number to 3 significant figures.
That is, we look at the first 3 non-zero digits of the number, which are 1, 2 and 5. We then look at the next digit after this to decide if the 3rd significant figure of 5 remains as a 5 or rounds up to a 6.
Only round up the 3rd significant figure if the 4th significant figure is equal to 5 or more.
Since the digit after the 5 is a 3, we do not round up.
We write 125 and then replace the other digits with zeros, so that 125364 written to 3 significant figures is 125000.
We now write this in scientific notation as 1.25 × 105, since there are 5 digits after the first digit of 1 in the number 125000.

For example, write the number 0.06627 in scientific notation to 3 significant figures.
Significant figures are counted after the zeros at the start of the number.
We look at the first 3 significant figures of the number which are 6, 6 and 2.
We only round up the 3rd significant figure if the 4th significant figure is equal to 5 or more.
The 4th significant figure is a 7 and so, we round the 2 up to a 3.
0.06627 rounded to 3 significant figures is 0.0663.
This number starts with 2 zeros, so writing it in scientific notation we have 6.33 × 10-2.

How to Add and Subtract Numbers in Scientific Notation
The ease of adding and subtracting numbers in scientific notation depends on whether the size of the exponents are the same in each number.
To add or subtract numbers in scientific notation that have the same exponent, simply add or subtract the coefficients and keep the exponent the same. For example, 3×105 + 4×105 is (3+4)×105 which equals 7×105.
In this example, the exponents on both 3×105 and 4×105 are both 5.
Therefore, we can simply add the 3 and the 4 together to obtain 7, whilst the exponent in the answer remains as 5.
3×105 + 4×105 = 7×105.
This addition is essentially the same as 300 000 + 400 000 = 700 000.

For example, 3×10-4 – 1×10-4 = (3-1)×10-4 which is just 2×10-4.
In this example, we simply subtract the coefficients and keep the exponent as -4.

To add or subtract numbers in scientific notation that have different exponents, it is easiest to convert the numbers to standard notation first. Then perform the addition or subtraction and write the result back in scientific notation if needed.
In the example of 3.21×103 + 2×104, the exponents are different sizes.
- Converting 3.21×103 to standard notation, we have 3 210. The exponent of 3 means there are 3 digits after the first digit.
After the 3, we have the 2 then the 1 and so, another digit of 0 is needed to make 3 digits after the first digit in total.
Converting 2×104 to standard notation, we have 20 000. That is, we have 4 digits after the first digit of 2.
Now, these numbers can be added following the standard addition process.
3 210 + 20 000 = 23 210.
We can write this in scientific notation if needed as 2.321×104 since there are 4 digits after the first digit in 23 210.

Here is an alternate method for adding numbers in scientific notation when they have different exponents.
The same numbers as above are used but here we are demonstrating a different method to solve the problem.
To add or subtract numbers in scientific notation, first convert the numbers to have the same exponent. To do this, multiply the coefficient of the number with the largest exponent by 10 each time the exponent is reduced by 1.
For example, in 3.21×103 + 2×104, we wish to reduce the exponent in 2×104 from a 4 to a 3 so that it is the same exponent as in 3.21×103.
Since we need to reduce the exponent by 1, we multiply the 2 by 10 to make 20.
2×104 is the same as 20×103.
Therefore 3.21×103 + 2×104 is rewritten as 3.21×103 + 20×103.
Now the coefficients can be added so that 3.21×103 + 20×103 = (3.21+20)×103.
This equals 23.21×103 which can be readjusted to 2.321×104 as we divide the coefficient by 10 as we increase the exponent of 10 by 1.


Here is an example of subtracting numbers in scientific notation by first converting them to have the same exponents.
In the example of 5.3×105 – 7.9×104 , we need to change the exponent of 5.3×105 to a 4.
To do this, we multiply the 5.3 by 10 to make 53.
5.3×105 is the same as 53×104.
Therefore 5.3×105 – 7.9×104 can be written as 53×104 – 7.9×104.
Now the numbers have the same exponent, subtract the coefficients like so:
(53 – 7.9)×104 = 45.1×104.
Finally, this is rewritten so that the coefficient is a number between 1 and 10. We divide 45.1 by 10 and increase the exponent by 1 to compensate.
45.1×104 = 4.51×105.

How to Multiply and Divide Numbers in Scientific Notation
To multiply numbers in scientific notation, multiply the coefficients and add the exponents. For example, (2×103) × (3×105) = 6×108. The coefficients of 2 and 3 were multiplied to make 6 and the exponents of 3 and 5 were added to make 8.
This occurs since exponents are always added when they are multiplied together.

Here is an example of multiplying numbers in scientific notation: (4.5×109) × (5.2×10-2).
Firstly, the coefficients of 4.5 and 5.2 are multiplied to obtain 23.4.
Secondly, the exponents are added so that 9 + -2 = 7.
Therefore, (4.5×109) × (5.2×10-2) = 23.4×107.
However, 23.4 must be written as a number between 1 and 10.
We divide 23.4 by 10 to obtain 2.34 and we increase the exponent from 7 to 8 to compensate.
(4.5×109) × (5.2×10-2) = 2.34×108.

To divide numbers in scientific notation, divide the coefficients and subtract the exponents. For example, (6×107) ÷ (2×102) = 3×105. The coefficients of 6 and 2 were divided to obtain 3 and the exponent of 2 was subtracted from the exponent of 7 to obtain 5.
This occurs since exponents are subtracted when they a division takes place.

Here is another example of dividing numbers in scientific notation: (8.4×104) ÷ (2.5×10-3).
Firstly, the coefficients are divided so 8.4 ÷ 2.5 = 3.36.
Secondly, the exponents are subtracted. 4 – -3 is the same as 4 + 3 which equals 7.
(8.4×104) ÷ (2.5×10-3) = 3.36×107.

Scientific Notation on Calculator
Scientific notation is commonly used in calculator displays.
To write scientific notation on a calculator, use the button labelled as ‘×10𝑥‘ or just 10𝑥‘.
- Enter the coefficient (the number between 1 and 10)
- Then press the ‘×10𝑥‘ button
- Then enter the power of 10

Here are the instructions for entering scientific notation on some common calculators:
Casio Fx-300
The ‘×10𝑥‘ button is found in the middle of the bottom row.
- Enter the coefficient (the number between 1 and 10)
- Then press the ‘×10𝑥‘ button
- Then enter the power of 10
Casio Fx-82
The ‘×10𝑥‘ button is found in the middle of the bottom row.
- Enter the coefficient (the number between 1 and 10)
- Then press the ‘×10𝑥‘ button
- Then enter the power of 10
Casio Fx-CG50
The ‘×10𝑥‘ button is found in the middle of the bottom row.
- Enter the coefficient (the number between 1 and 10)
- Then press the ‘×10𝑥‘ button
- Then enter the power of 10
Ti-30XB
The ’10𝑥‘ option is found above the ‘log’ button. Press ‘2nd’ then ‘log’ to write numbers in scientific notation.
- Enter the coefficient (the number between 1 and 10)
- Press the ‘2nd’ button
- Then press the ‘log’ button to select the ’10𝑥‘ option
- Then enter the power of 10
Ti-84
The ’10𝑥‘ option is found above the ‘log’ button. Press ‘2nd’ then ‘log’ to write numbers in scientific notation.
- Enter the coefficient (the number between 1 and 10)
- Press the ‘2nd’ button
- Then press the ‘log’ button to select the ’10𝑥‘ option
- Then enter the power of 10
