Video Lesson
How to Calculate Reverse Percentages
All percentage changes can be reversed to find an original amount. The process of calculating an original amount following a percentage change is known as finding a reverse percentage.
Reverse percentages are commonly used to find the original price of an item after a percentage change (discount or tax).
The method and process described on this page explains how to reverse a given percentage increase or decrease to find an original amount.
To reverse a percentage change:
- Write the percentage change as a decimal multiplier.
- Divide the new amount by the decimal multiplier.

To calculate the decimal multiplier:
- If the percentage change is an increase, add it to 100% or if the percentage change is a decrease, subtract it from 100%.
- Divide this new percentage by 100 to make the decimal multiplier.
To find an original number after a percentage change, divide the new number by the decimal multiplier
The trick for finding reverse percentages
For example: A television is on sale with a 10% discount. The sale price of the television is $990. What did it cost before the sale?
100% – 10% = 90% so following the 10% discount, the television is at 90% of its original price. The decimal multiplier is 0.90.
The original cost of the television is equal to the sale price of the television divided by the decimal multiplier.
Therefore the original price of the television = $990 ÷ 0.90 = $1100.
Example of finding an original amount after a percentage decrease:
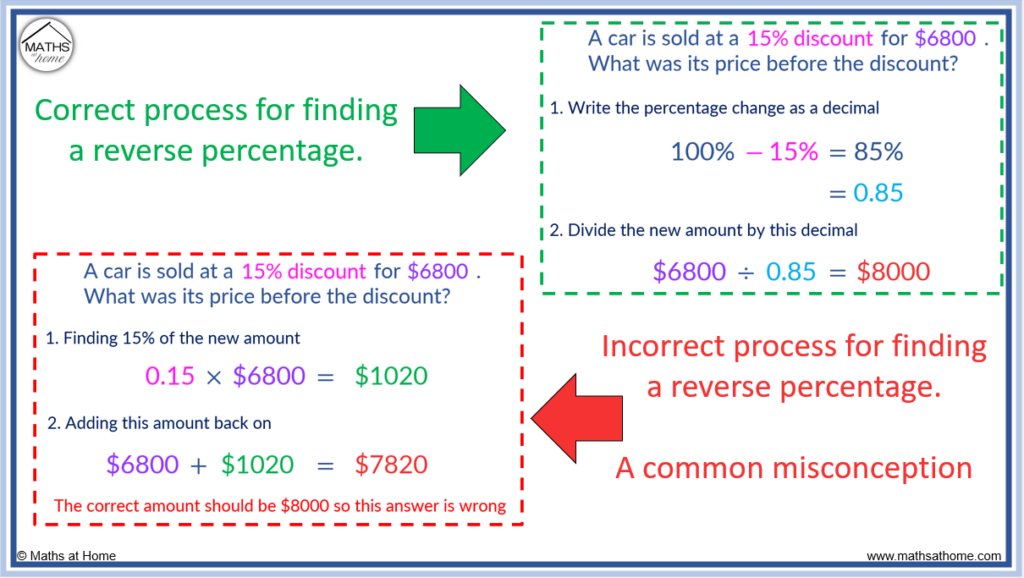
A car is sold at a 15% discount for $6800. What was its price before the discount?
In this example, the new price of a car was 15% less than its original price. So the original price we are calculating will be higher than $6800.
Step 1. Write the percentage change as a decimal multiplier
The original price of the car is 100%.
A discount is a percentage decrease therefore we subtract 15% from 100%.
100% – 15% = 85%
We now divide this percentage by 100 to write it as a ‘decimal multiplier’.
85% ÷ 100 = 0.85

Step 2. Divide the new amount by this decimal multiplier
The new amount is is the current price of the car, which is $6800.
In Step 1. we found that the decimal multiplier was 0.85.
We divide the new amount by the decimal multiplier.
$6800 ÷ 0.85 = $8000
Therefore, the original price of the car before the discount was $8000.

The explanation of the mathematics in this example is that the car was originally more expensive before the discount.
It was $8000 and after a discount of 15% its new value was $6800.
We reduced 100% by 15% to get 85% of the total price. Basically, $6800 was 85% of the original price.
Multiplying $8000 by 0.85 would reduce the original price to the new price of $6800.
Therefore dividing $6800 by 0.85 ‘reversed’ this process so we could find that the original price was $8000.
Dividing by a decimal number between 0 and 1 will make a number larger.
$6800 divided by 0.85 became $8000
Misconceptions of Calculating Reverse Percentages
Misconceptions around calculating reverse percentages are almost always to do with deviating from the correct process. The most common misconception is finding the given percentage of the new amount and then simply adding or subtracting this back on to the new amount. This is incorrect because we need to find the given percentage of the original amount not the new amount.This misconception can be illustrated using the example above:
A car is sold at a 15% discount for $6800. What was its price before the discount?
The 15% discount is 15% of the original amount. That is 15% of $8000.
- 15% of $8000 is $1200.
However, the common mistake is to find 15% of the new amount.
- 15% of $6800 is only $1020.
Therefore we cannot simply find 15% of the known new amount and add it back on.
If we add $1020 back on to $6800, we obtain an original amount of $7820 which is the incorrect answer. It should be $8000.
This is because we need to add 15% of the original amount and add this back on. 15% of $8000 is $1200 and $6800 + $1200 takes us to the correct answer of $8000.
However, since we do not know the original amount, we need to follow the two step process listed above which is to find the decimal multiplier and divide the new amount by this to find the original amount.
The comparison of the correct and incorrect methods are shown below.
The order in which percentages are calculated matters.
To teach reverse percentages, it is important to distinguish between the large variety of methods for each percentage type so that students know when to use the correct process.
Reverse percentage questions can be identified as questions that tell you the new amount and ask you to find an original amount.
With these questions, the easiest way to calculate the original amount is to divide the new amount by the decimal multiplier.
Questions that tell you the original amount and as you to calculate the new amount are not reverse percentage questions.
In these type of questions, you need to find the given percentage and simply add or subtract it to or from the original amount.
An example of this type of question would be:
A car costs $2000 and its price is increased by 15%. Find the new price of the car.
Since we are asked to find the new value, this is not a reverse percentage question.
We simply find 15% of $2000 and add this on to $2000.
0.15 × $2000 = $300 and so, the new price is $2000 + $300 = $2300.
Example of finding an original amount after a percentage increase
Here is an example of calculating a reverse percentage following a percentage increase:
The population of a town grew by 5.1% and is now 8408. What was the population before?
Step 1. Write the percentage change as a decimal multiplier
The population grew by 5.1%, which means that it increased.
100% is the original population size.
100% + 5.1% = 105.1%
We then divide this percentage by 100 to find the decimal multiplier.
105.1% ÷ 100 = 1.051

Step 2. Divide the new amount by this decimal multiplier
The population is now 8408 and so the new amount is 8408.
The decimal multiplier was calculated in step 1 as 1.051.
To find the original amount, divide the new amount by the decimal multiplier.
8408 ÷ 1.051 = 8000
Therefore there were 8000 people in the town before it grew by 5.1%.

The original population was 8000 people. It grew by 5.1% to become 8408 people.
We divided 8408 by 1.051 to reverse the percentage increase and obtain the original amount of 8000.
How to Reverse any Percentage Change
The following tables list the divisions that should be performed to calculate a given reverse percentage. Simply divide the new amount by the given number in order to calculate the original amount before the percentage change occurred.
For example:
- If a painting increased in price by 10% to $220, the original price can be found by dividing $220 by 1.1 to obtain $200.
- If the amount of fuel decreased by 20% to 640 L, the original amount can be found by dividing 640 mL by 0.8 to obtain 800 mL.
| Percentage increase to be reversed | Calculation |
| 10% increase | ÷ 1.1 |
| 20% increase | ÷ 1.2 |
| 25% increase | ÷ 1.25 |
| 30% increase | ÷ 1.3 |
| 40% increase | ÷ 1.4 |
| 50% increase | ÷ 1.5 |
| 60% increase | ÷ 1.6 |
| 70% increase | ÷ 1.7 |
| 75% increase | ÷ 1.75 |
| 80% increase | ÷ 1.8 |
| 90% increase | ÷ 1.9 |
| 100% increase | ÷ 2 |
| 150% increase | ÷ 2.5 |
| 200% increase | ÷ 3 |
| Percentage decrease to be reversed | Calculation |
| 10% decrease | ÷ 0.9 |
| 20% decrease | ÷ 0.8 |
| 25% decrease | ÷ 0.75 |
| 30% decrease | ÷ 0.7 |
| 40% decrease | ÷ 0.6 |
| 50% decrease | ÷ 0.5 |
| 60% decrease | ÷ 0.4 |
| 70% decrease | ÷ 0.3 |
| 75% decrease | ÷ 0.25 |
| 80% decrease | ÷ 0.2 |
| 90% decrease | ÷ 0.1 |
| 95% decrease | ÷ 0.05 |
All percentages can be reversed. The table above simply lists a few common examples.
Reverse Percentages using the Unitary Method
To calculate reverse percentages using the unitary method:
- Write the new amount as a percentage of the original amount.
- Divide the new amount by this percentage value to obtain the size of 1%.
- Multiply this by 100 to obtain the original amount of 100%.
Example of using the unitary method to reverse a percentage decrease
For example we will consider the same example we used previously for finding the price of a car:
A car is sold at a 15% discount for $6800. What was its price before the discount?
This is how to find the price of a discounted item.
Step 1. Write the new amount as a percentage of the original amount
The car is discounted by 15%.
Therefore 100% – 15% = 85% and so, the new price of $6800 is 85% of the original price.
We write: 85% = $6800
Step 2. Divide the new amount by this percentage value to obtain the size of 1%
Since 85% = $6800, we divide by 85 to obtain:
1% = $80
Step 3. Multiply by 100 to obtain the original amount of 100%
Since:
1% = $80
We multiply by 100 to obtain:
100% = $8000
Therefore, the original amount was $8000.

100% is always the value of the original amount and is always the answer to the reverse percentage calculation.
The unitary method of calculating reverse percentages involved calculating 1% of the original value and then multiplying this by 100 to obtain 100% of the original value.
Example of using the unitary method to reverse a percentage increase
A shirt costs $68.75 after a tax of 25% has been added. What was the cost of the shirt before the tax?
This is how we find the original price after the percentage increase.
Step 1. Write the new amount as a percentage of the original amount
The original price of the shirt is equal to 100%.
25% has been added onto this price so that 100% + 25% = 125%.
Therefore the increased price of $68.75 is equal to 125%.
125% = $68.75
Step 2. Divide the new amount by this percentage value to obtain the size of 1%
Dividing by 125 we obtain:
1% = $0.55
Step 3. Multiply by 100 to obtain the original amount of 100%
Since 1% = $0.55, we can multiply by 100 to obtain:
100% = $55.00
Therefore the shirt was $55 before the 25% tax was added to it.

Reverse Percentages: Algebraic Method
An algebraic method may be used to teach the reverse percentage process.
To calculate a reverse percentage using algebra:
- Write the original amount required as ‘𝑥’.
- Write the percentage multiplier multiplied by ‘𝑥’ equal to the new amount.
- Divide both sides by the percentage multiplier to calculate the original amount ‘𝑥’.
For example: A car is sold at a 15% discount for $6800. What was its price before the discount?
Step 1. Write the original amount required as ‘𝑥‘
The original price of the car is denoted as 𝑥.
This is the answer that we will calculate.
Step 2. Write the percentage multiplier multiplied by ‘𝑥’ equal to the new amount
The price was discounted by 15%.
Therefore the original amount of 100% was reduced by 15% so that 100% – 15% = 85%.
Therefore the new amount of $6800 is 85% of the original amount.
This means that the original amount of ‘𝑥’ was multiplied by 0.85 to obtain $6800.
We write 0.85𝑥 = $6800
Step 3. Divide both sides by the percentage multiplier to calculate the original amount ‘𝑥’
If 0.85𝑥 = $6800, then we can calculate 𝑥 by dividing both sides of the equation by 0.85.
$6800 ÷ 0.85 = $8000. Therefore:
𝑥 = $8000

Here is an example of using algebra to calculate a reverse percentage:
A shirt costs $68.75 after a tax of 25%. What was the cost of the shirt before tax?
Step 1. Write the original amount required as ‘𝑥‘
The original price of the shirtis denoted as 𝑥.
This is the answer that we will calculate.
Step 2. Write the percentage multiplier multiplied by ‘𝑥’ equal to the new amount
The price was increased due to the tax by 25%.
Therefore the original amount of 100% was increased by 25% so that 100% + 25% = 125%.
Therefore the new amount of $68.75 is 125% of the original amount.
This means that the original amount of ‘𝑥’ was multiplied by 1.25 to obtain $68.75.
We write 1.25𝑥 = $68.75
Step 3. Divide both sides by the percentage multiplier to calculate the original amount ‘𝑥’
If 01.25𝑥 = $68.75, then we can calculate 𝑥 by dividing both sides of the equation by 1.25.
$68.75 ÷ 1.25 = $55.00. Therefore:
𝑥 = $55

Calculating Reverse Percentages without a Calculator
A reverse percentage can be calculated without a calculator by using simple percentage calculations.
Finding 10% or 5% of the original amount can be useful as we can multiply these by 10 or 20 respectively to find 100%.
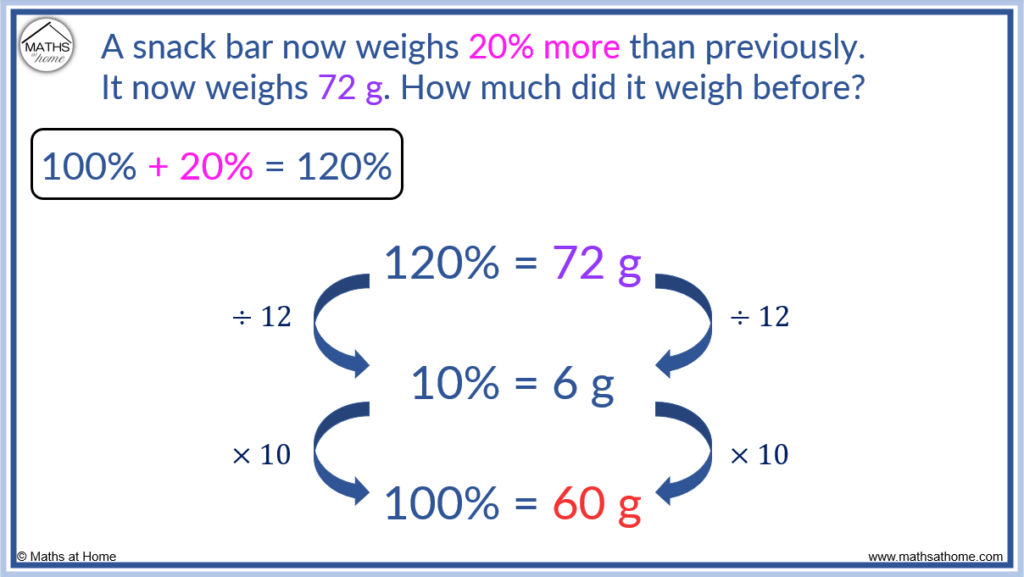
For example: A snack bar now weighs 20% more than previously. It now weights 72 g. How much did it weigh before?
Since the snack bar increased in size by 20%, we now have 120%.
120% = 72 g
We need to calculate 100%, so we can first find 10% and then multiply this by 10.
Since 120% = 72 g, we can divide by 12 to obtain 10%. Since 72 ÷ 12 = 6, we can write:
10% = 6 g
We then multiply 10% by 10 to obtain 100%. Therefore:
100% = 60 g
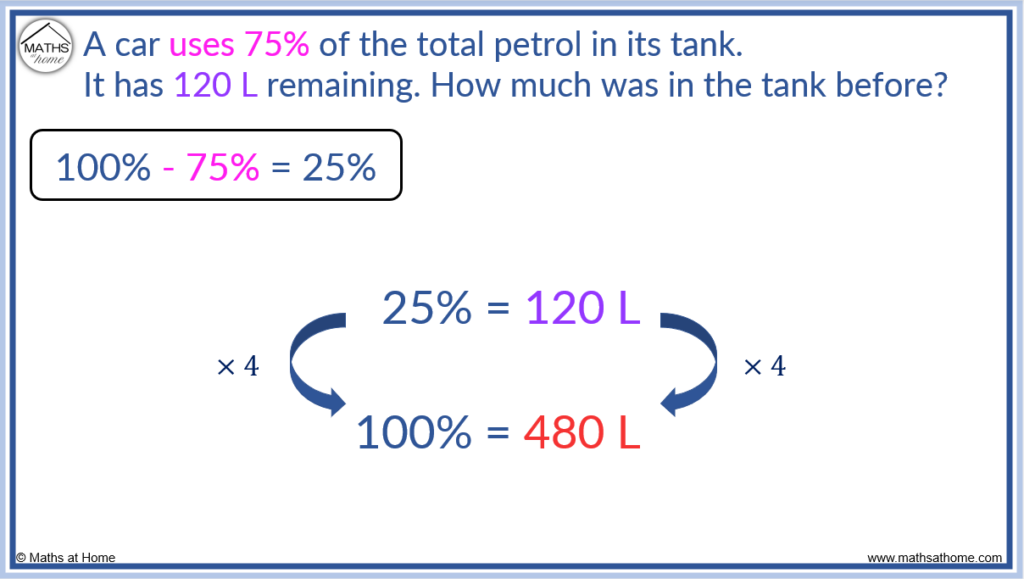
Here is another example of calculating reverse percentages without using a calculator:
A car uses 75% of the total petrol in its tank. It has 120 L remaining. How much was in the tank before?
100% is the amount that was in the tank before the petrol was used. It is the amount that we wish to calculate.
75% of the petrol was used so that there is 100% – 75% = 25% of the petrol remaining.
Therefore, the remaining 120 L is equal to 25% of the total amount. We write:
25% = 120 L
Now 25% goes into 100% four times. So we simply multiply this amount by 4 to obtain the answer.
100% = 480 L
Doing this calculation without a calculator, we can double it and double it again to multiply by 4.
120 L doubled is 240 L and doubling again, we obtain 480 L.
Reverse Percentages Formula
The formula to calculate a reverse percentage is: original amount = new amount ÷ decimal multiplier, where the decimal multiplier = (100% + percentage change) ÷ 100.

For example: A sightseeing tour costs $85.80 including GST at 10%. What is the cost of the tour before GST is added?
GST is the ‘Goods and Services Tax’ and we are told that it is at 10%. This means that an extra 10% of the cost of the tour has been added on to the original price.
This means that the percentage change is 10%. It is a positive value since it was added on to the original amount.
The decimal multiplier = (100% + percentage change) ÷ 100.
The decimal multiplier = (100% + 10%) ÷ 100.
This equals 110% ÷ 100 = 1.1.
We now use the formula of Original Amount = New Amount ÷ Decimal Multiplier to calculate the original cost of the tour before GST was added.
Original Amount = $85.80 ÷ 1.1 = $78. Therefore the original cost of the tour before tax was $78.
How to do Reverse Percentages with Compound Interest
Reverse percentages can be used to calculate an original amount following on from compound interest using the formula: Original Amount = New Amount ÷ (1+i)n ,where i is the interest rate as a decimal and n is the number of compounding periods.
For example: An amount was deposited into a savings account with an interest rate of 2.5% compounded annually. The money was left in the account for 3 years so that there is now $2261.47 in the account. How much money was deposited into the account originally?
- Since the interest rate is 2.5%, i = 0.025
- Since the money is in the account for 3 years, n = 3
- The new amount is 2261.47
We can use the formula: Original Amount = New Amount ÷ (1+i)n
So the original amount = 2261.47 ÷ (1+0.025)3.
We obtain an original amount of $2100.
Therefore $2100 was deposited into the account originally.

How to do Reverse Percentages using Excel
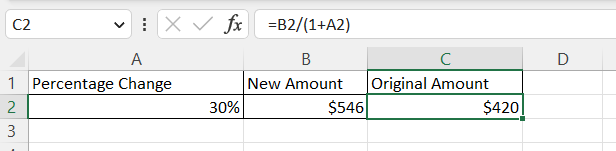
To calculate a reverse percentage using Excel, use the formula: =B2/(1+A2), where B2 is the new amount and A2 is the percentage change. Ensure that the % sign is entered in cell A2 and that any percentage decreases are entered as a negative percentage.
For example, an amount was increased by 30% so that the new amount is $546.
Using this formula, the original amount before the increase was found to be $420.
- The percentage change of 30% is listed in cell A2
- The new amount of $546 is listed in cell B2
- The original amount is calculated in cell C2 using the formula: =B2/(1+A2)
If the percentage change was a decrease or reduction, the percentage change is entered as a negative value.
For example, an amount was decreased by 15% so that the new amount is $51.
Using this formula, the original amount before the decrease was found to be $60.
- The percentage change of 15% is listed in cell A2
- The new amount of $51 is listed in cell B2
- The original amount is calculated in cell C2 using the formula: =B2/(1+A2)
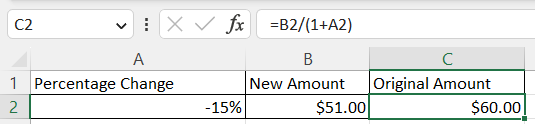
Here, the percentage change was entered as a negative value since it was a percentage decrease. That is, this amount was removed from the original price, not added to it.
We can see that the calculated original price is larger than the new price, which is what we would expect.
