Logarithm Laws: Video Lesson
What are the Laws of Logarithms?
The laws of logarithms are algebraic rules that allow for the simplification and rearrangement of logarithmic expressions. The 3 main logarithm laws are:- The Product Law: log(mn) = log(m) + log(n).
- The Quotient Law: log(m/n) = log(m) – log(n).
- The Power Law: log(mk) = k·log(m).
The three fundamental laws of logarithms are shown below.

Rules when using the Laws of Logarithms
The rules for the laws of logarithms are:
- To simplify logarithms with the product or quotient laws, the bases of the logarithms must be equal.
- The base of the logarithms must be greater than zero.
- The base of the logarithms cannot be equal to 1.
- The inputs of the logarithms must be greater than zero.
- The logarithm of 1 is equal to zero, no matter what the base of the logarithm is.
The three fundamental laws of logarithms can also be written as:
- loga(m) + loga(n) = loga(mn)
- loga(m) – loga(n) = loga(m/n)
- loga(mk) = kloga(m)

Examples of Using Logarithm Laws
The three most important logarithm laws are shown below with an example of each.

When adding logarithms with the same base, the inputs to the logarithms can be multiplied.
The 4 and 5 inside the logarithms are multiplied to obtain 20.

When subtracting logarithms with the same base, the first logarithm is divided by the logarithm being subtracted.
10 is divided by 5 inside the logarithm to obtain log(2).

The coefficient of the logarithm can be moved to become the power of the input to the logarithm.
5 is raised to the power of 2 to obtain 25.
List of the Logarithm Laws
The following table shows the complete list of log laws with examples of how they are used:
| Logarithm Law | Formula | Example |
| Product Law | loga(m) + loga(n) = loga(mn) | log(2) + log(3) = log(6) |
| Quotient Law | loga(m) – loga(n) = loga(m/n) | log(12) – log(3) = log(4) |
| Power Law | loga(mk) = k ·loga(m) | log(9) = log(32) = 2log(3) |
| Inverse Logarithm Property | loga(ak) = k | log2(8) = log2(23) = 3 |
| Zero Law | loga(1) = 0 | log3(1) = 0 |
| Logarithm of a Reciprocal | loga(1/m) = -loga(m) | log(1/2) = -log(2) |
| Identity Property of a Logarithm | loga(a) = 1 | log5(5) = 1 |
| Inverse Property of an Exponent | aloga(k) = k | 3log3(5) = 5 |
| Change of Base Law | loga(m) = logc(m)/logc(a) | log2(5) = log3(5)/log3(2) |
Here is a visual list of 5 of the most commonly used logarithm laws.
The colours used in this list show how the different rearrangements are made in a more simple, visual manner.

The following sections take a look at each of the logarithm laws in greater detail.
The logarithm laws are:
- The Product Rule
- The Quotient Rule
- The Power Rule
- The Inverse Property of Logarithms
- The Zero Rule
- The Identity Rule
- The Inverse Property of the Exponent
The Product (Addition) Logarithm Law
To add two or more logarithms that have the same base, simply multiply the numbers inside the logarithms. For example, log(3)+log(2) = log(6). The result is a single logarithm with the same base as those being added.

The formula for the product law of logarithms is given as:
The product rule of logarithm laws
Two logarithms can only be simplified using the addition (product) rule if they have the same base. This base remains the same in the resulting answer.
For example, log3(2) + log3(5) = log3(2 × 5) = log3(10).

Here is another example of adding logarithms using log laws and then simplifying.
log4(2) + log4(8) = log4(16)
Since two logarithms of the same base were added, the resulting logarithm input was equal to the product of the inputs given.
Now log4(16) = 2 because 42 = 16.
A logarithm simply asks what power the base of the logarithm must be raised to in order to obtain the input.
4 must be raised to the power of 2 to obtain 16 and so, the final answer of this question is just 2.

The product rule for logarithms can also be written in reverse using the formula:
The product rule of logarithm laws
The product rule of logarithms states that a single logarithm can be separated into the sum of individual logarithms which have inputs that multiply to make the input of the original logarithm.
For example, log(21) = log(3) + log(7).
Here are some examples of how to add logarithms using the addition log law.
| Question | Solution | |
| log(5) + log(3) | = log(5×3) | = log(15) |
| log3(2) + log3(7) | = log3(2×7) | = log3(14) |
| log(2) + log(3) + log(4) | = log(2×3×4) | = log(24) |
| log(1) + log(20) + log(0.25) | = log(1×20×0.25) | = log(5) |
| ln(4) + ln(5) | = ln(4×5) | = ln(20) |
| log(𝑥2) + log(y) | = log(𝑥2 × y) | = log(𝑥2y) |
The Quotient (Subtraction )Logarithm Law
Logarithms of the same base can be subtracted by dividing their inputs. For example, log(8) – log(4) = log(2), since 8 ÷ 4 = 2. The result is a single logarithm with the same base as those being subtracted.

The formula for subtracting logarithms using the quotient law is given as:
The quotient law of logarithms
Two or more logarithms can only be simplified using the quotient law if they have the same base. The input of the first logarithm is divided by the input of the logarithm being subtracted. The result is a single logarithm with the same base.
For example, log3(20) – log3(4) = log3(5).
The result is a single logarithm, also base 3.

Here is another example of subtracting logarithms using the quotient logarithm law.
log5(100) – log5(4) = log3(100 ÷ 4) which equals log5(25).
log5(25) can be evaluated since 25 is a power of 5.
52 = 25 and so, log5(25) = 2.

The quotient rule for logarithms can also be written in reverse using the formula:
The product rule of logarithm laws
The quotient rule of logarithms states that a single logarithm can be written as a logarithm subtracted from another logarithm.
For example, log(2/5) = log(2) – log(5).
Here are some examples of how to subtract logarithms using the subtraction log law.
| Question | Solution | |
| log(10) – log(2) | = log(10÷2) | = log(5) |
| log3(6) – log3(3) | = log3(6÷3) | = log3(2) |
| log(20) – log(2) – log(5) | = log(20÷2÷5) | = log(2) |
| log(30) – log(5) – log(1) | = log(30÷5÷1) | = log(6) |
| ln(12) – ln(6) | = ln(12÷6) | = ln(2) |
| log(𝑥2) – log(y) | = log(𝑥2 ÷ y) | = log(𝑥2/y) |
The Logarithm Law for Exponents
If there is a coefficient in front of a logarithm, the power law of logarithms states that the input to the logarithm can be raised to the power of this coefficient. For example, 2log(3) = log(32) which equals log(9).

The formula for the power law of logarithms is:
The power law of logarithms
For example, 3log2(10) can be written as log2(103).
This is because the coefficient of 3 immediately in front of the log can be moved so that it is acting as a power on the number inside the log.
Now log2(103) = log2(1000).

Reciprocal Rule of Logarithms
When the reciprocal of the input to a logarithm is taken, the result is equal to -1 multiplied by the logarithm of the original input. That is log(1/b) = -log(b). For example, log(1/2) = -log(2).
We can see that since then
.
We can use the power law of logarithms to move the power of -1 down to become the coefficient of the logarithm so that or more simply,
.

For example, .

The formula for the reciprocal of the input to a logarithm is given by:
Reciprocal of the input to a logarithm
The reciprocal logarithm law can be applied in the following circumstances.
(since both sides of the equation equal zero)
Logarithms Involving a Square Root
When the coefficient of a logarithm is equal to one half, the input inside the logarithm can be raised to the power of this half. Raising a value to the power of one half is equivalent to finding its square root. Therefore (1/2)loga(b) = loga(√b). For example, (1/2)log(16) = log(√16) = log(4).
The formula for the a logarithm with a coefficient of one half is given as:
Formula for a logarithm with a coefficient of one half
In the example below, using the power logarithm law, (1/2)log(16) = log(161/2).
When 16 is raised to the power of one half, it is equivalent of finding the square root of 16.
Therefore (1/2)log(16) = log(161/2) = log(√16) = log(4).

In general, .
And so, the formula for any fractional coefficient of a logarithm is:
Formula for a fractional coefficient of a logarithm
For example, and so,
.
The Inverse Property of Logarithms
The inverse property of logarithms states that loga(ak) = k. When the base number inside the logarithm is equal to the base of the logarithm, the result is simply the value of the exponent inside the logarithm. For example, log3(35) = 5.
The formula for the inverse property of logarithms is:
The Inverse Property of Logarithms

The other example of the inverse property of logarithms listed above is .
That is because when 2 is raised to the power of 𝑥, we obtain 2𝑥.
Logarithm Law: The Zero Rule
The logarithm of one is equal to zero no matter what the base of the logarithm is. That is, loga(1) = 0 for all valid values of ‘a’. Some of the many examples include: log2(1) = 0, log5(1) = 0, log(1) = 0 and ln(1) = 0.
This rule is true since the value of a logarithmic expression is always equal to the power that the base of the logarithm must be raised to in order to obtain the value of the input of the logarithm.
Since any positive or negative number raised to the power of zero is equal to 1 (that is, a0=1), then loga(1) must be equal to 0.

Logarithm Law: The Identity Rule
The identity rule of logarithms states that if the input to a logarithm is equal in value to the base of the logarithm, the result is equal to 1. That is, loga(a) = 1. For example, log3(3) = 1 and log2(2) = 1.

This rule works since a logarithmic expression is equal in value to the power that its base must be raised to in order to obtain the value which is the input to the logarithm.
Since a1 = a, then loga(a) must equal 1.
The identity rule of logarithms is applied to natural logarithms in the sense that ln(e) = 1. This is because ln(e) means loge(e).
Logarithm Law: Inverse Property of Exponents
The inverse property of exponents states that if a given number is raised to the power of a logarithm which has the same base as this given number, then the result is simply equal to the input of the logarithm. That is, aloga(k) = k. For example, 2log2(5) = 5.

The inverse property of exponents can be applied to natural logarithms in the following manner:
eln(k) = k
This is true since ln(k) means loge(k).
For example, eln(2) = 2.
Logarithm Laws: Examples and Solutions
Here are some examples with solutions of using logarithm laws to simplify and expand expressions.
It is important to understand that the addition and subtraction logarithm laws can only be used when we have one logarithm added to or subtracted from another logarithm and there are no coefficients in front of either logarithm.
Therefore, it is important to always use the power logarithm law to move any coefficients from in front of the logarithms before adding or subtracting them.
For example, use logarithm laws to simplify .
Both logarithms have coefficients and so, we use the power log law so that and
.
Therefore we know that and
.
Therefore becomes
.
Now that the coefficients have been moved and we simply have one logarithm plus another logarithm, we can add them using the addition (product) law of logarithms.
We simply multiply the inputs of 4 and 1000.
.

Here is another example of simplifying a logarithmic expression using logarithm laws.
Simplify .
We move the coefficients first so that they become the powers of the inputs to the logarithm.
In the first logarithm:
and in the second logarithm: .
Therefore becomes
.
Since the logarithms have the same base, we can subtract them using the subtraction (quotient) law.
We simply divide 8 by 2 to obtain 4.
.

Here are some further examples of using logarithm laws:
- Simplify
.
All logarithms are the same base and so we multiply the numbers in the logarithms that are being added and then divide by the number inside the logarithm being subtracted.
Therefore:
- Simplify
.
Both 16 and 2 are powers of 2, which is the base of the logarithms.
We can write as
which is equal to 4.
is just equal to 1.
Therefore, and so, the answer is 5.
…
Alternatively, we can use the addition (product) law immediately so that .
Then we can use the fact that 25=32 to evaluate .
- Evaluate
.
We can use the subtraction (quotient) law so that .
Using the fact that log(100) means log10(100) and also the fact that 102=100, we can evaluate log(100) = 2.
Therefore .
- Expand the logarithmic expression of
.
Since the 25, ,
and z are multiplied together inside the logarithm, we can write
.
We can see that log5(25) = 2 since 52 = 25.
Therefore .
We can then use the power law to bring the coefficients down in front of the logarithms to obtain:
.
- Expand the logarithmic expression
.
All terms on the top of the fraction are multiplied together and so, can be written as the summation of individual logs. The term on the bottom of the fraction are subtracted as we are dividing by this.
We write .
We can write log2(6) as log2(2) + log2(3).
We can therefore write log2(6) as 1 + log2(3).
Therefore .
Finally, we can bring down the power of 5 on the final logarithm using the power law.
.
- Expand the logarithmic expression of
.
We can write .
We can then write this as .
We bring down the power using the power law so that .
Finally, we use the fact that ln(e) = 1 so that:
.
Expanding Logarithms Using Logarithm Laws
Single logarithms can be expanded into multiple logarithms of the same base using logarithm laws.
For example, using the addition (product) law, we can write log(20) as log(20) = log(5) + log(4).
Then log(4) can also be written as log(22), which can be written as 2log(2).
Therefore log(20) can be written as log(20) = log(5) + 2log(2).

Here is another example of expanding a logarithmic expression using logarithm laws.
Using the addition and subtraction logarithm laws, we can write .
All terms on top of the fraction inside the logarithm are positive and the log(y5) is subtracted since it has been divided inside the logarithm.
We can then use the power law of logarithms to bring down the powers as coefficients.
We can also evaluate log(10) = 1.
Therefore .

Change of Base Rule
The change of base formula for logarithms is loga(b) = logc(b) ÷ logc(a). For example log2(10) = log(10) ÷ log(2).
The change of base logarithm formula is:
The change of base logarithm formula
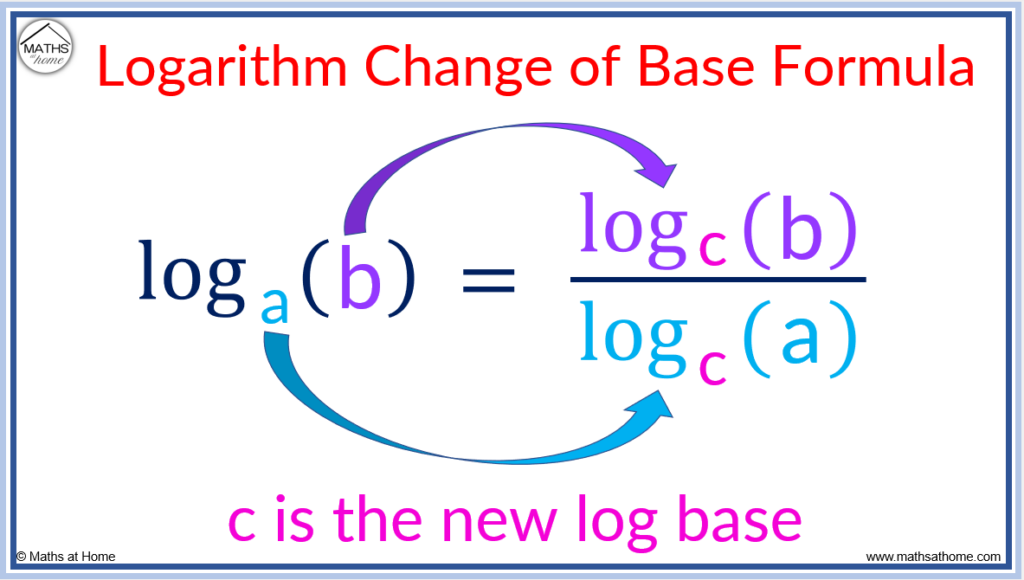
To divide logarithms that have the same base, the change of base formula can be used. That is, logc(b) ÷ logc(a) = loga(b). For example, log2(27) ÷ log2(3) = log3(27) and this can be evaluated since log3(27) = 3.
Proof of the Logarithm Laws
The following is the algebraic proof of the product (addition) law of logarithms.
- Let
and take logarithms of both sides to obtain
. Then use the power law of logarithms to bring the power of m down as the coefficient of the logarithm. That is,
.
- Take
and follow the same process as above to obtain
.
- Multiply
and
to obtain
which is more simply written as
.
- Take logarithms of both sides to obtain
. Then use the power law of logarithms to bring the (m+n) down as the coefficient of the log so that
.
- Then expand the brackets to obtain
.
- Finally substitute
and
from the previous calculations so that
becomes
.

The following is the algebraic proof of the quotient (subtraction) law of logarithms:
- Let
and take logarithms of both sides to obtain
. Then use the power law of logarithms to bring the power of m down as the coefficient of the logarithm. That is,
.
- Take
and follow the same process as above to obtain
.
- Divide 𝑥 by y so that
and so,
.
- Take logarithms of both sides so that
.
- This can be written using the power law of logarithms as
.
- Expanding the brackets,
.
- Finally substitute
and
from the previous calculations so that
becomes
.

The following is algebraic proof of the exponent (power) law of logarithms:
- Consider the expoenential equation of
and write this in logarithmic form as
.
- Returning to
and raise both sides to the power of k to obtain
.
- This can be written more simply as
.
- Now write
in logarithmic form as
.
- Now substitute
as previously found into
in order to obtain
.
- This can be written in the more familiar format as
.

