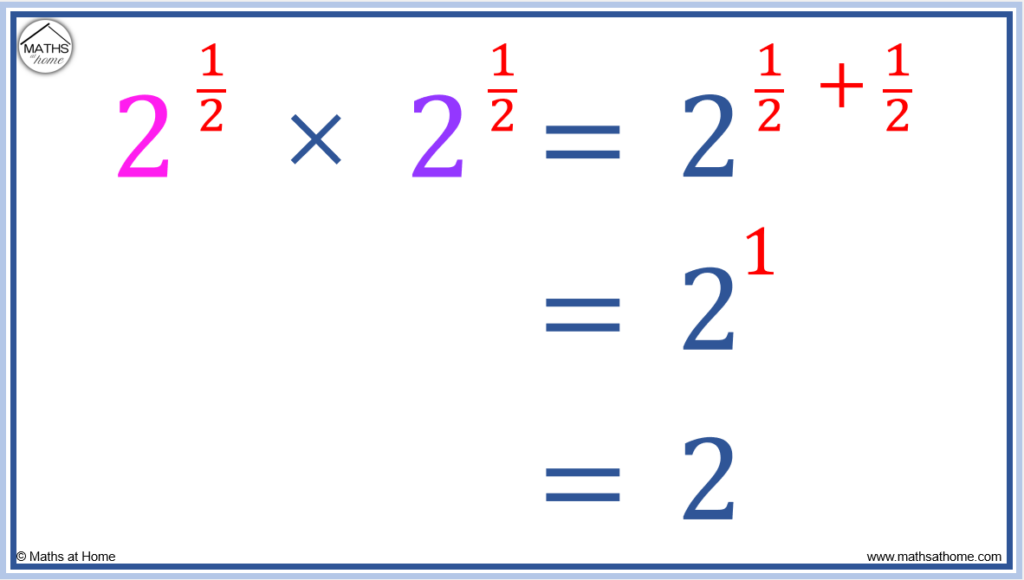A Complete Guide to Multiplying Exponents

Video Lesson: How to Multiply Exponents

Rules for Multiplying Terms with Exponents

• If the base number is the same, keep the base number the same and add the exponents.
• If the base numbers are different but the exponent is the same, multiply the base numbers and raise it to the same exponent.
• If the base number and the exponents are different, then work out each of the terms separately and then multiply them.

How to Multiply Exponents with the Same Base

To multiply terms with the same base, add their exponents. For example, 𝑥⁵ × 𝑥⁴ = 𝑥⁹, since 5 + 4 = 9.

which simplifies as .

To multiply exponents with the same base, keep the base the same and only add the exponents. For example, 3² × 3³ = 3⁵.

Notice that we add the exponents of 2 + 3 = 5 but we keep the base number as 3.

We don’t multiply the base numbers together.

It does not matter how many terms there are, if terms with the same base are multiplied, add the exponents.

For example, in the question :

Here can be written as since a is the same as a¹.

Therefore and so, .

How to Multiply Exponents with Coefficients and Variables

To multiply exponential terms with variables and coefficients, multiply the coefficients and add the exponents of each different variable separately. For example, 2𝑥⁵ × 3𝑥⁴ = 6𝑥⁹. This is because the coefficients are multiplied with 2 × 3 = 6 and the exponents are added with 5 + 4 = 9.

Coefficients are the numbers at the front of each term. We multiply these when we multiply terms because they are normal numbers that multiply when we have a multiplication sign.

• So 2 × 3 = 6

The exponents on each variable behave according to laws of exponents. That is, we actually add them when we have a multiplication sign.

• So 5 + 4 = 9

Therefore: 2𝑥⁵ × 3𝑥⁴ = 6𝑥⁹.

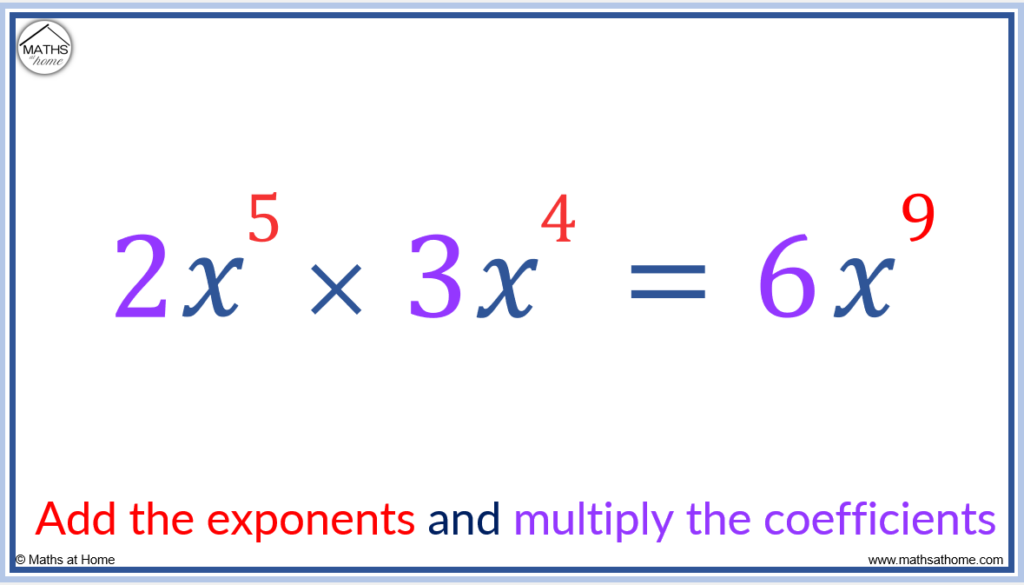
How to Multiply Exponents with Many Variables

To multiply terms that have different variables, multiply the coefficients and then add the exponents of each variable separately, letter by letter. For example in 5𝑥²y³ × 2𝑥³y⁴, the coefficients are multiplied so that 5 × 2 = 10, then the exponents on 𝑥 are added so that 2 + 3 = 5 and finally, the exponents on y are added so that 3 + 4 = 7. Therefore 5𝑥²y³ × 2𝑥³y⁴ = 10𝑥⁵y⁷.

• 5 × 2 = 10
• 𝑥² × 𝑥³ = 𝑥⁵
• y³ × y⁴ = y⁷

---

Here is another example of multiplying variables with exponents: simplify 4a²b × 5ab⁵.

• 4 × 5 = 20
• a² × a is the same as a² × a¹ which equals a³
• b × b⁵ is the same as b¹ × b⁵ which equals b⁶

Therefore 4a²b × 5ab⁵ = 20a³b⁶.

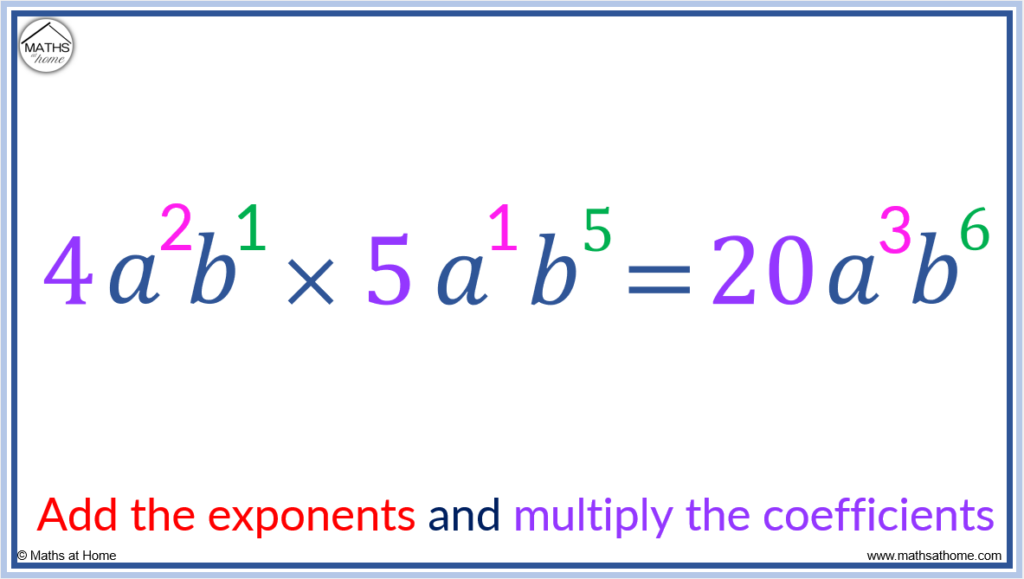
How to Multiply Negative Exponents

To multiply terms with negative exponents, we add the exponents in the normal manner. For example a⁸ × a^-3 = a^8+-3 which is the same as a^8-3 which equals a⁵.

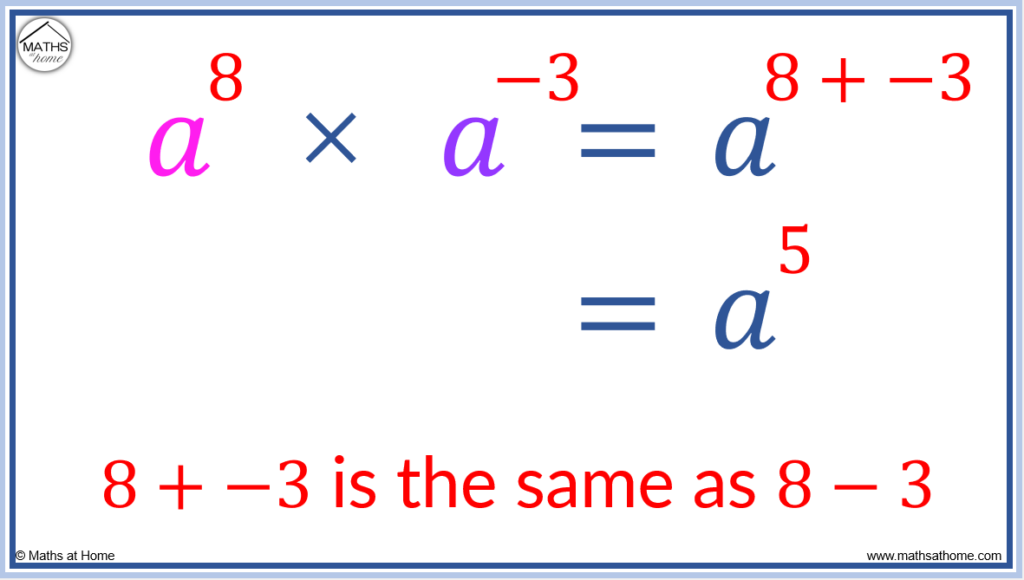
The following rules are used to add negative numbers when multiplying exponents:

• ‘+-‘ and ‘-+’ can both be replaced with a subtraction ‘-‘
• -a-b = -(a+b)

For example, 5^-2 × 5^-1 = 5^-2+-1.

5^-2+-1 is the same as 5^-2-1 which equals 5^-3.

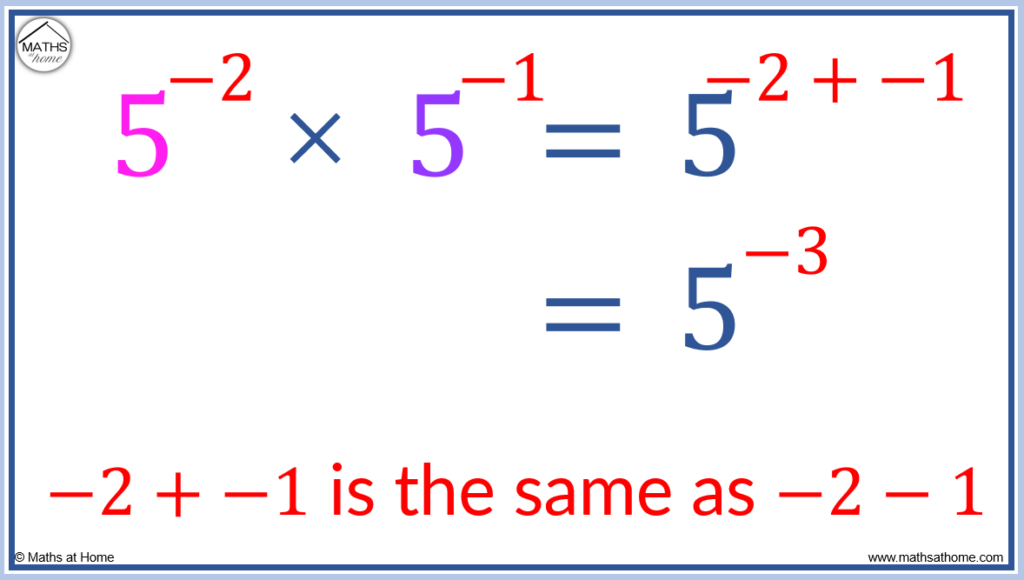
Here is another example of multiplying exponents with negative indices.

c^-6 × c⁴ = c^-6+4 which equals c^-2.

To calculate -6+4, it can be easier to calculate 4-6 to obtain -2.

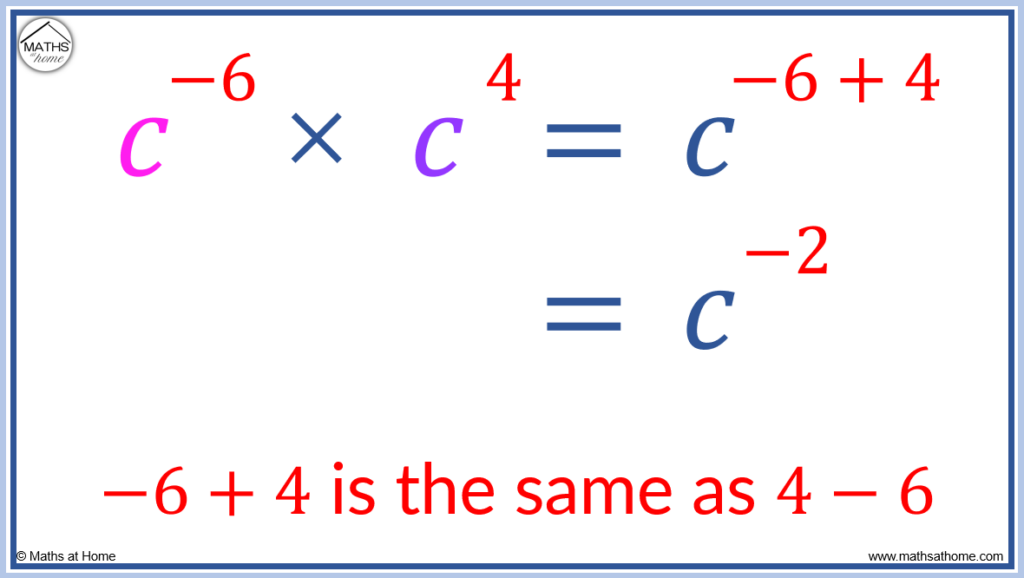
Examples of Multiplying Exponents

Here are some examples of multiplying terms containing exponents:

Multiplying Exponents Question	Answer
x3 × x2 =	x5
x2 × x4 × x5 =	x11
x × x2 =	x3
x-4 × x2 =	x-2
x5 × x-2 =	x3
x-3 × x-5 =	x-8
x-3 × x8 =	x5
2x3 × 3x5 =	6x8
10x2 × 2x × 3x3 =	60x6
5x3y2 × 2x5y2 =	10x8y4
-10xy × 3x4y	-30x5y2

Formula for Multiplying Exponents with the Same Base

The formula for multiplying exponential terms with the same base is a^m × aⁿ = a^m+n.

The formula for multiplying exponential terms

For example, in this question we multiply exponents of ten: :

• a= 10
• m = 3
• n = 6

Therefore becomes since 3 + 6 = 9.

We can multiply exponents of Euler’s number, ‘e’ in the same manner.

To multiply exponents with ‘e’, we add the exponents.

Why do we Add Exponents When we Multiply them?

When two terms with the same base are multiplied, we add the exponents. This is because the exponent acting on a number tells us how many times that number is multiplied. This effect is combined when two exponents are multiplied.

To understand why we add exponents when two terms are multiplied, it is best to consider an example.

• 3² means 3 × 3
• 3³ means 3 × 3 × 3

Therefore 3² × 3³ is the same as (3 × 3) × (3 × 3 × 3) and this equals 3⁵ since there are 5 threes multiplied in total.

How to Multiply Exponents with Different Bases

Terms with the same exponent and different bases can be multiplied using the formula a^m × b^m = (a × b)^m. For example, 2² × 3² = (2 × 3)².

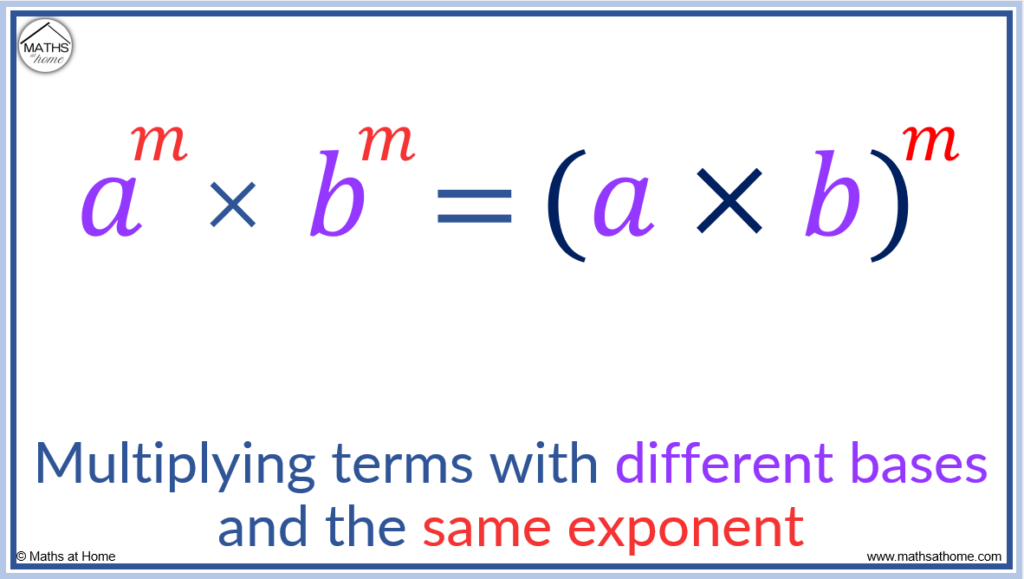
In the example of 2² × 3², the bases are different but the exponents are the same. Both numbers are raised to the power of 2.

That means the two base numbers can be multiplied first and then raised to the power of 2.

Using the formula of a^m × b^m = (a × b)^m, we have:

• a = 2
• b = 3
• m = 2

And so, a^m × b^m = (a × b)^m becomes 2² × 3² = (2 × 3)².

Therefore 2² × 3² = 6² which equals 36.

---

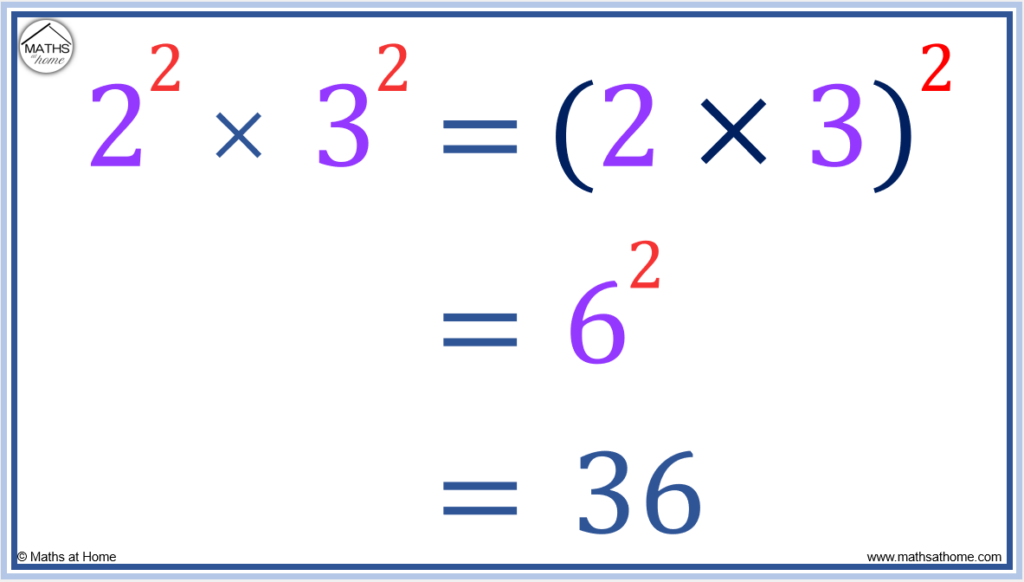
Here is another example of 5⁶ × 2⁶.

Calculating 5⁶ and 2⁶ and then multiplying them together can be quite time consuming.

In this instance, it is easier to use the rule of a^m × b^m = (a × b)^m, where:

• a = 5
• b = 2
• m = 6

Therefore, 5⁶ × 2⁶ = (5 × 2)⁶.

This is easier to calculate because we obtain 10⁶. Finding powers of 10 is easy because the power of 6 tells us that there are 6 zeros in the answer.

10⁶ = 1 000 000.

Therefore 5⁶ × 2⁶ = 1 000 000.

Multiplying Exponents with Square Roots

Finding the square root of a value is the same as raising it to the power of one half. For example √2 × √2 is the same as 2^½ × 2^½. Then adding the exponents, we obtain 2¹. Therefore √2 × √2 = 2.

One half add one half equals one whole and therefore 2^½ × 2^½ = 2.