How to Calculate the Percentage Error (Pictures and Examples)

Video Lesson: Calculating Percentage Error

The Percentage Error Formula

The formula to calculate percentage error is:

Percentage Error = |[(Measured Value – True Value) / True Value]| x 100

Where the Measured Value is the value obtained through measurement or observation.

Where the True Value is the actual, theoretical or accepted value of the quantity being measured.

The absolute value is used to ensure that the error is always positive.

$P e r c e n t a. g of e e r r o r equals the absolute value of the fraction with numerator M e a. s u r e d V a. l u e minus T r u e V a. l u e and denominator T r u e V a. l u e times 100 percent sign$
Formula for calculating the percentage error

The absolute value “| |” is used to ensure that the percentage error calculated is postive.

The absolute value operation means to take the result of $the fraction with numerator M e a. s u r e d V a. l u e minus T r u e V a. l u e and denominator T r u e V a. l u e$ and make it positive.

So if the result of this part of the formula is negative, it becomes positive and if it is already positive, it remains as positive.

This calculation tells us the absolute error.

For example: My height is measured as 182 cm but my actual height is 174 cm. Find the percentage error in the measurement.

The measured value is 182 cm
The true value is 174 cm

The formula of $P e r c e n t a. g of e e r r o r equals the absolute value of the fraction with numerator M e a. s u r e d V a. l u e minus T r u e V a. l u e and denominator T r u e V a. l u e times 100 percent sign$

becomes $the absolute value of the fraction with numerator 182 minus 174 and denominator 174 times 100 percent sign$ which becomes .

We obtain which equals .

The percent error in the height measurement is 4.60%.

how to find the percentage error with the formula

For example: I measure 33 g of a substance but there is actually 40 g. Find the percentage error in the measurement.

In this example the measured value is lower than the true value and so, the absolute value operation “| |” will be used to make the answer positive.

The measured value is 33 g.
The true value is 40 g.

Therefore the formula of $P e r c e n t a. g of e E r r o r equals the absolute value of the fraction with numerator M e a. s u r e d V a. l u e minus T r u e V a. l u e and denominator T r u e V a. l u e times 100 percent sign$ becomes:

$the absolute value of the fraction with numerator 33 minus 40 and denominator 40 times 100 percent sign$ which is .

The absolute value “| |” is used to turn the -7 into a positive 7 so the calculation becomes: .

Evaluating this, we obtain and so, the absolute percentage error is .

Steps to Find the Percent Error

The percent error formula can be broken down into three simple steps based on the order of the calculations.

Following these steps will find the same result as using the percentage error formula but some people may prefer this method.

To calculate the percent error in steps:

Find the difference between the true value and the measured value.

Divide this result by the true value.

Multiply this result by 100.

For example: I measure 26 mL of liquid but the true amount there is 21 mL. Find the percentage error in measurement.

Step 1. Find the difference between the true value and the measured value

The measured value is 26
The true value is 21

The difference between the values is found by subtracting the smaller value from the larger value.

26 – 21 = 5 and so, the difference between the measured and true value is 5.

Step 2. Divide this result by the true value

The true value is 21 and so we divide 5 by 21.

5 ÷ 21 ≈ 0.238.

Step 3. Multiply this result by 100

0.238 × 100 = 23.8

Therefore the percentage error is 23.8%.

Percentage errors are often measured to 3 significant figures and can take decimal values.

What is Percentage Error and Why is it Important?

Percentage error is the difference between a measurement and its actual value. This difference is expressed as a percentage of the actual value. It is used in scientific experiments to compare an experimental value to the expected or known value.

The percentage error is simply given as a percentage without any units.
The larger the percentage error, the greater the inaccuracy in the experiment or measurement.
A smaller percentage error indicates a greater level of precision and accuracy.

Percentage error is a measure of how different an experimental result is from the expected or true value. This is important in scientific experiments where small errors can be very significant.

Percentage error can be used to determine the accuracy and reliability of results.
Measuring percentage error can be useful as adjustments can be made to the experimental methods to reduce the error of future experiments.
Percentage error can be used to identify apparatus malfunction or imprecision of equipment.
Percentage error can be used in manufacturing processes to identify sources of errors so that a better product can be made.
Percentage error can be used to improve the quality and efficiency of manufacturing processes and reduce waste.

Percentage error is also known as relative error. This is because the difference between the measured and true values is always compared relative to the true value.

What is an Acceptable Percentage Error?

The acceptable level of percentage error depends on the level of accuracy required for the experiment and the precision of the measuring instruments involved. Many scientific experiments may allow a 1% error as a result of imprecision in the instruments however in high-precision, medical or safety experiments the acceptable error may be 0.1% or lower.

As a rule, large percentage error is not good and reducing the percentage error present is always positive.

In situations where a certain degree of variability is expected, a higher percentage error may be acceptable. For example, a percentage error of 5% may be acceptable in public opinion polls.

It is possible to have 0% percentage error. This occurs when the measured value is identical to the true value and there is no difference or error present).

Percentage Error over 100%

A percentage error of 100% means that the measured result is double the true value. Therefore it is a significantly large error. Percentage errors larger than 100% can occur and they mean that the measured result is more than double the true value.

For example:

A percentage error of 100% means the measured value is double the true value
A percentage error of 200% means the measured value is triple the true value
A percentage error of 300% means the measured value is quadruple the true value
A percentage error of 400% means the measured value is five times the true value

While a percentage error over 100% may seem extreme, it can still be useful to calculate and report it as it still provides information on the magnitude of the error. However, it is important to consider the context of the measurement or calculation and the potential sources of error that may have contributed to such a large percentage error.

In general, a percentage error over 100% suggests that there may be significant issues with the measurement or calculation, and further investigation and re-evaluation may be necessary to ensure accuracy.

Negative Percentage Error

In the percentage error formula, the absolute value operation ensures that all percentage errors are given as a positive value. However, it can be useful to calculate negative percentage errors which tell us that the measured value is less than the true value. If negative percentage errors are desired, do not take the absolute value in the percentage error calculation.

$P e r c e n t a. g of e E r r o r equals the fraction with numerator M e a. s u r e d V a. l u e minus T r u e V a. l u e and denominator T r u e V a. l u e times 100 percent sign$
The percentage error formula including negative percentage errors

Positive percentage error means that the measured result is larger than the true value
Negative percentage error means that the measured result is less than the true value

For example, we can see that compared to the true value of 50, the measured values below that are above 50 have a positive percentage error and the measured values below 50 have a negative percentage error.

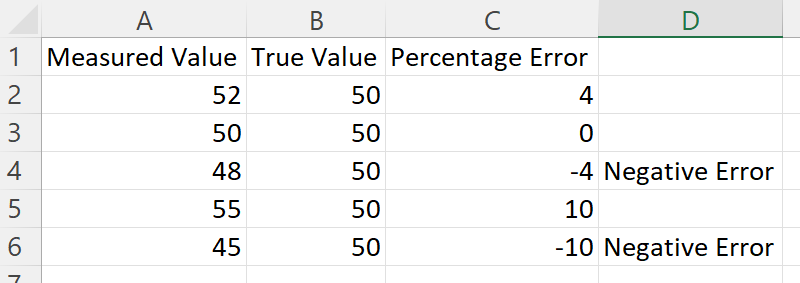
While negative percentage errors can be less common than positive percentage errors, they are still important to report as they provide valuable information on the accuracy of the measurement or calculation.

Negative percentage errors help indicate how many results are above or below the expected value and as such, they can be used to improve the accuracy of an experiment.

Examples of Calculating Percentage Error

Here are some examples of calculating the percentage error.

Measured Value	Actual Value	Calculation	Percentage Error
50 m	40 m	\|[(50 – 40) / 40]\| x 100 =	25%
8 L	10 L	\|[(8 – 10) / 10]\| x 100 =	20%
152 cm	142 cm	\|[(152 – 142) / 142]\| x 100 =	7.04%
23 g	25 g	\|[(23 – 25) / 25]\| x 100 =	8%
30°	26°	\|[(30 – 26) / 26]\| x 100 =	15.9%

Percentage Error for Multiple Trials

To find the percentage error for multiple trials of an experiment, calculate the average of these values and use this average in place of the measured value in the percent error formula.

The formula then becomes:

$P e r c e n t a. g of e E r r o r equals the absolute value of the fraction with numerator open paren A v e r a. g of e V a. l u e minus T r u e V a. l u e close paren and denominator T r u e v a. l u e times 100 percent sign$
Formula for the Percentage Error for Multiple Trials

The steps for calculating the percentage error for multiple trials are:

Calculate the average of the measured values by adding them all together and dividing by the number of trials.

Calculate the difference between the average measured value and the actual value using absolute value.

Divide this difference by the actual value.

Multiply the result by 100 to convert it to a percentage.

For example, 5 trials were conducted to determine the mass of an object which obtained the following results: 10.2 g, 10.1 g, 10.3 g, 10.0 g, and 10.2 g.

The mass of the object is known to be 10.5 g.

Find the percentage error for these 5 trials.

Calculate the average measured value:

Average measured value = (10.2 + 10.1 + 10.3 + 10.0 + 10.2) / 5 = 10.16 g

Calculate the difference between the average measured value and the actual value using absolute value:

Percent error = [(|10.16 – 10.5|) / 10.5] x 100%

Percent error = [0.34 / 10.5] x 100%

Percent error = 3.24%

Therefore, the percent error for these 5 trials is 3.24%.

How to Calculate the Percentage Error in Excel

To find the percentage error using Excel, use the following formula:

=ABS((Measured Value - True Value) / True Value) * 100

To use this formula:

Enter the measured value in one cell, say A2.
Enter the true value in another cell, say B2.
Enter the above formula in a cell and replace “Measured Value” with the cell reference of the measured value (A2) and “True Value” with the cell reference of the true value (B2).

With a measured value in cell A2 and a true value in cell B2, the excel formula to find the percentage error becomes:

=ABS((A2-B2)/B2)*100

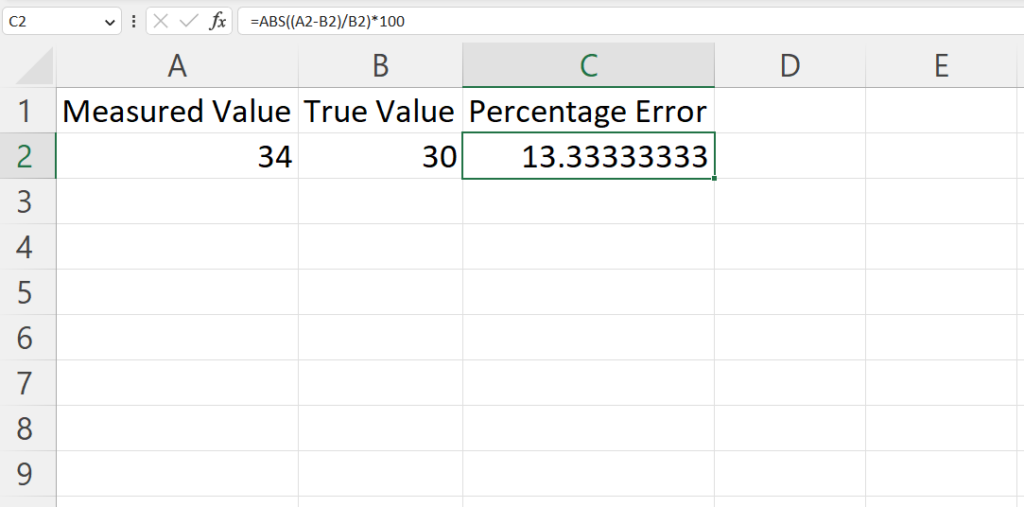
how to find the percentage error on excel

Note that the ABS function is used to get the absolute value of the difference between the actual and estimated value. Multiplying the result by 100 converts the value to a percentage.

For example in the cells above, the measured value of 34 is in cell A2 and the true value of 30 is in cell B2.

In cell C2 we type “=ABS((A2-B2)/B2)*100 and press enter.

The result of 13.3% error is obtained.