How to Find the Modulus and Argument of a Complex Number

Video Lesson: How to Find the Modulus and Argument of a Complex Number

What is the Modulus of a Complex Number?

The modulus is the distance of the complex number from the origin on the argand diagram. For any complex number z = a + bi, the modulus is calculated using the Pythagorean theorem with the formula |z| = √(a2 + b2).

The complex number forms a right-angled triangle on the complex plane as shown below.

The modulus is equal to the length of the vector from the origin to the point of the complex number. That is, it forms the hypotenuse of the right-angled triangle with ‘a’ and ‘b’ forming the two shorter sides.

definition of the modulus of a complex number

The modulus (also known as the magnitude or absolute value) of a complex number is a scalar value that represents the distance of the complex number from the origin on the complex plane. It is a non-negative real number as it represents a distance.

the absolute value of z equals the square root of a. squared plus b squared

The formula for the modulus of a complex number

How to Find the Modulus of a Complex Number

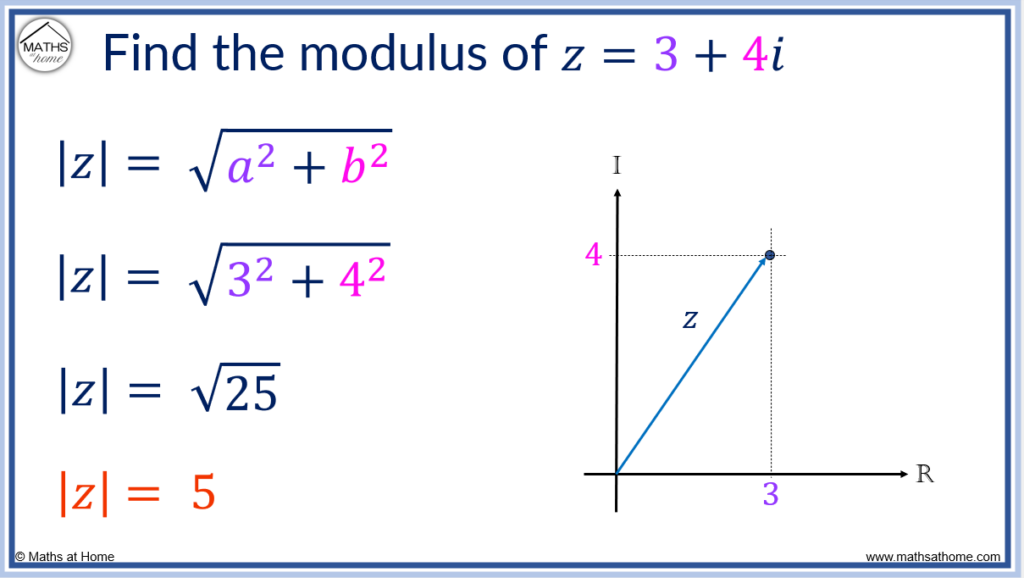
To calculate the modulus of a complex number, z = a + bi, use the formula |z| = √(a2 + b2). For example, the modulus of z = 3 + 4i is |z| = √(32 + 42). Simplifying this, the modulus is found to be |z| =√25 which can be evaluated as |z| = 5.  

formula for finding the modulus of a complex number

Example: Find the modulus of z equals 3 plus 4 i.

  • ‘a’ is the size of the real part of the number. Therefore a = 3.
  • ‘b’ is the size of the imaginary part of the number. Therefore b = 4.

the absolute value of z equals the square root of a. squared plus b squared becomes the absolute value of z equals the square root of 3 squared plus 4 squared.

Evaluating this, the absolute value of z equals the square root of 9 plus 16 and so, the absolute value of z equals the square root of 25.

The size of the modulus is the absolute value of z equals 5.

example of how to find the modulus of a complex number
To calculate the modulus of a complex number in steps:

  1. Square the size of the real part of the complex number.
  2. Square the size of the imaginary part of the complex number.
  3. Add the two results together.
  4. Square root this result.

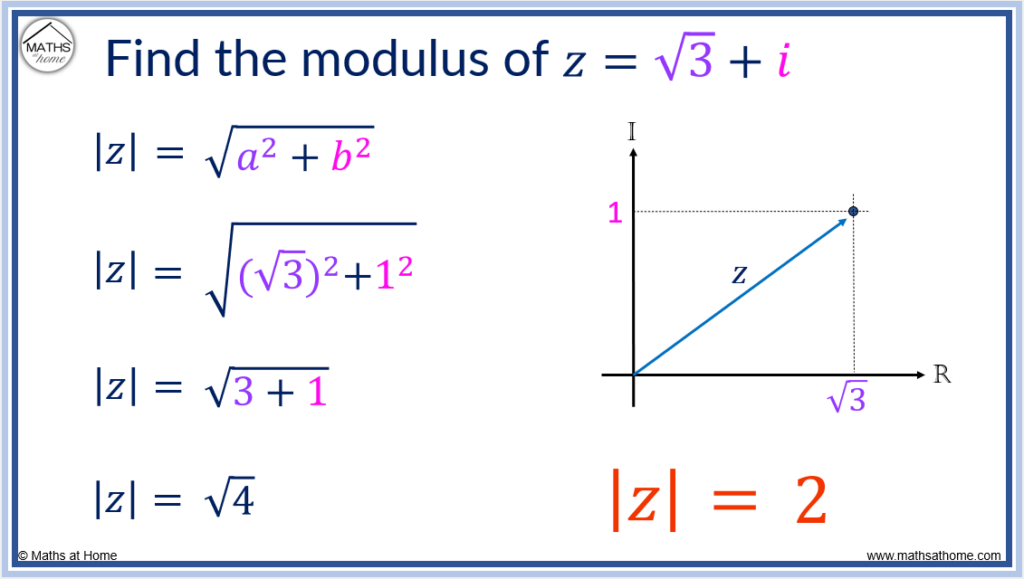
For example: Find the modulus of z = √3 + i.

Step 1. Square the size of the real part of the complex number

The real part of  z equals the square root of 3 plus i is the part without an i.

That is, the real part is √3.

Squaring this, open paren the square root of 3 close paren squared equals 3.

Step 2. Square the size of the imaginary part of the complex number

The imaginary part of z equals the square root of 3 plus i is the part with the i.

That is, the imaginary part is just i, which is the same as 1i.

 The size of the imaginary part is 1.

Squaring this, 1 squared equals 1.

Step 3. Add the two results together

3 + 1 = 4

Step 4. Square root this result

the square root of 4 equals 2 and so, the modulus is the absolute value of z equals 2.

how to find the modulus of sqrt3+i

The following table contains some examples of calculating the modulus of a complex number:

Complex NumberModulus CalculationModulus
z = 1 + 3i√(12 + 32) √10 
z = 1 + i√(12 + 12) √2
z = -1 + 5i√( (-1)2 + 52) √
z = i√(12) √1
z = -2i√( (-2)2 ) √2

How is the Modulus of a Complex Number Used?

Some of the most common uses of the modulus in mathematics, physics and engineering include:

  1. Calculating the distance from the origin: The modulus of a complex number is the distance of the number from the origin on the complex plane. It can be used to calculate the distance between two complex numbers.
  2. Writing the polar form of a complex number: The modulus of a complex number is used to express the number in polar form, where the modulus is the magnitude or radius and the argument is the angle the complex number makes with the positive x-axis.
  3. Writing the modulus-argument form of a complex number: The modulus and argument of a complex number can be used to represent the complex number in modulus-argument form.
  4. Complex Amplitude: In signal processing and physics, the modulus of a complex number can be used to represent the amplitude of a signal.
  5. Inverse trigonometric functions: The modulus of a complex number is used when finding the inverse trigonometric functions of complex numbers, which is useful in physics and engineering.
  6. Determining the stability of a system: In control systems, the modulus of a complex number can be used to determine the stability of a system.

Properties of the Modulus of a Complex Number

The following are some key properties of the modulus of a complex number:

  1. The modulus of a complex number is a non-negative real number. This means that the modulus will always be greater than or equal to zero. That is, the absolute value of z is greater than or equal to 0.
  2. If the modulus of a complex number is zero, then the complex number is z = 0.
  3. The modulus is commutative for multiplication and division. That is, the absolute value of z sub 1 z sub 2 equals the absolute value of z sub 1 times the absolute value of z sub 2 and the absolute value of the fraction with numerator z sub 1 and denominator z sub 2 equals the fraction with numerator the absolute value of z sub 1 and denominator the absolute value of z sub 2.
  4. The modulus of a complex number is invariant under rotation of the complex plane. This means that the modulus does not change when the complex number is rotated in the complex plane.
  5. The modulus of a complex number is equal to the modulus of its conjugate. This means that the modulus of a + bi is the same as the modulus of a – bi. That is, the absolute value of z equals the absolute value of z horizontal bar and the absolute value of negative z equals the absolute value of negative z horizontal bar.
  6. Triangular inequality: The modulus of a complex number satisfies the triangle inequality, which states that the sum of the absolute values of any two complex numbers must be greater than or equal to the absolute value of their sum. That is, the absolute value of z sub 1 minus the absolute value of z sub 2 is less than or equal to the absolute value of z sub 1 plus z sub 2 is less than or equal to the absolute value of z sub 1 plus the absolute value of z sub 2.
  7. The modulus of a complex number raised to a power is equal to the modulus of the complex number raised to that power. That is, the absolute value of z to the power of n equals the absolute value of z to the power of n.
  8. The square of the modulus of a complex number is equal to the difference between the complex number and the conjugate of the complex number. That is, z minus z horizontal bar equals the absolute value of z squared.
  9. If a complex number has a modulus of 1, that is |z|=1, then it is known as unimodular.

What is the Argument of a Complex Number?

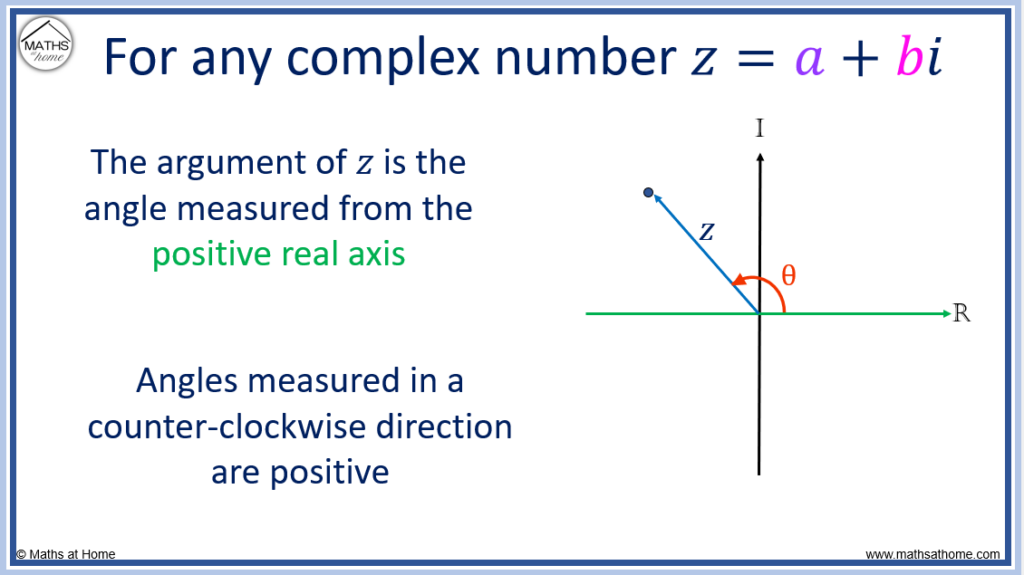
The argument (also known as the phase or amplitude) of a complex number is the angle that the vector representing the number makes with the positive real axis in the complex plane. It is typically denoted by the Greek letter “phi” (φ) measured in radians between the interval –π and π.

The argument of a complex number can be written as arg(z) for short.

The argument is always measured from the positive real axis, which is the right facing direction.

definition of the argument of a complex number

The argument of a complex number is periodic with a period of 2π. Therefore the general argument of a complex number is represented by θ + 2πk.

The principal argument of a complex number is defined as the angle measured from the positive real axis, taking values in the interval –π ≤ θ ≤π.

Angles measured from the positive real axis in the counter-clockwise direction are positive.

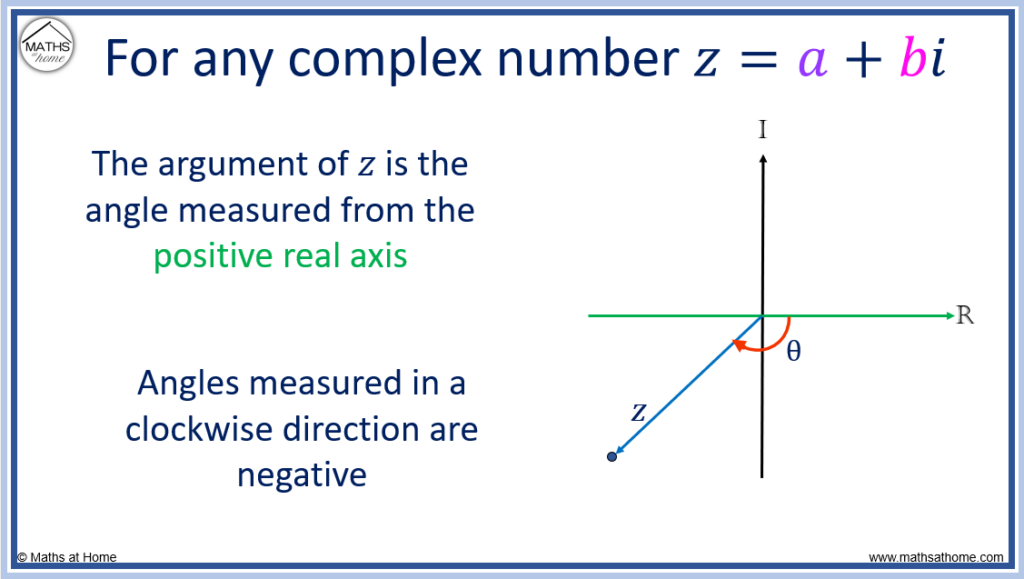
Angles measured from the positive real axis in the clockwise direction are negative.

a complex number with a positive argument
A positive argument angle
a complex number with a negative argument
A negative argument angle

How to Find the Argument of a Complex Number

To calculate the argument of a complex number z=a+bi:

  • First calculate θ=tan-1(b/a).
  • If the complex number is in quadrant 1, the argument is equal to θ.
  • If the complex number is in quadrant 2, the argument is equal to π+θ.
  • If the complex number is in quadrant 3, the argument is equal to θ-π.
  • If the complex number is in quadrant 4, the argument is equal to θ.
how to find the argument of a complex number

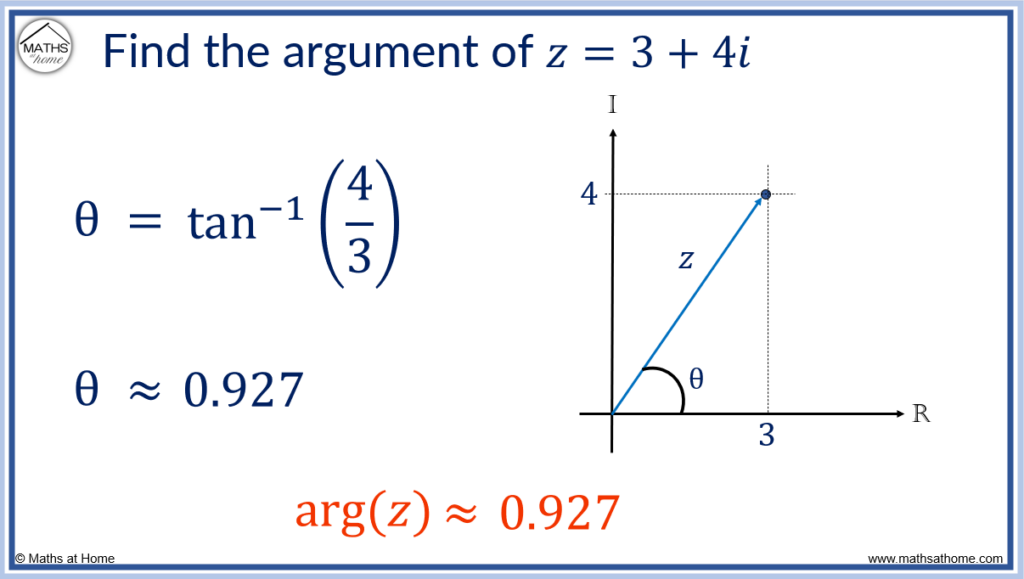
For example, find the argument of z equals 3 plus 4 i.

Step 1. First calculate θ=tan-1(b/a)

‘a’ is the size of real part of the number and ‘b‘ is the size of the imaginary part of the number.

In the complex number, z equals 3 plus 4 i:

  • a. equals 3
  • b equals 4

Therefore theta equals the inverse tangent of open paren b over a. close paren becomes theta equals the inverse tangent of four thirds and so, theta almost equals 0.927.

Step 2. The complex number is in quadrant 1 and the argument is equal to θ

Since the complex number is in quadrant 1 of the argand diagram, the argument is equal to θ.

Therefore, arg z almost equals 0.927.

example of how to find the argument of a complex number

Example of calculating the argument of a complex number in the third quadrant: z equals negative 1 minus 2 i

The complex number is in the third quadrant as shown in the argand diagram below.

The argument is shown by the angle θ, which is a negative angle measured clockwise from the positive real axis.

Step 1. First calculate θ=tan-1(b/a)

‘a’ is the size of real part of the number and ‘b‘ is the size of the imaginary part of the number.

In the complex number, z equals negative 1 minus 2 i

  • a. equals negative 1
  • b equals negative 2

Therefore theta equals the inverse tangent of open paren b over a. close paren becomes theta equals the inverse tangent of open paren negative 2 over negative 1 close paren and so, theta almost equals 1.11.

Step 2. The complex number is in quadrant 3 and the argument is equal to θ–π

The argument is the nearest angle to the complex number direction as measured from the positive real axis (from the right).

Since the complex number is in the third quadrant, the argument is calculated as θ – π.

theta almost equals 1.11 and so, arg z almost equals 1.11 minus pi.

Therefore the argument is given by arg z almost equals negative 2.03.

The argument of a complex number is negative when the nearest angle to the direction of the complex number from the positive real axis is clockwise.

finding the argument of a complex number in the third quadrant

Here are some further examples of calculating the argument of a complex number.

The argument is calculated using the following rules:

For a complex number z equals a. plus b i, the angle theta equals the inverse tangent of open paren b over a. close paren.

  • If the complex number is in quadrant 1, the argument is equal to θ.
  • If the complex number is in quadrant 2, the argument is equal to π+θ.
  • If the complex number is in quadrant 3, the argument is equal to θ-π.
  • If the complex number is in quadrant 4, the argument is equal to θ.
Complex NumberQuadrantθ CalculationArgument Calculation
-1-i3arctan(-1/-1) = π/4π/4 – π = -3π/4
1-√3i4arctan(-√3/1) = –π/3–π/3
3-√3i4arctan(-√3/3) = –π/6–π/6
1+√2i1arctan(2/1) = 0.9550.955
-1+i2arctan(1/-1) = –π/4-π/4 + π = 3π/4

Here are some examples of complex numbers with no real part

  • z=i has an argument of π/2
  • z=-i has an argument of –π/2

These arguments cannot be calculated using arctan since their real component is zero.

Any complex number that has no real part will lie on the imaginary axis.

If it is a positive complex number, it will be located on the imaginary axis above the real axis and so, its argument will be π/2.

If it is a negative complex number, it will be located on the imaginary axis below the real axis and so, its argument will be -π/2.

Modulus and Argument of a Complex Number Written in Exponential Form

For a complex number written in the exponential form as z = Reiφ, R is the modulus and φ is the argument. For example, if z = 3eπi, the modulus is equal to 3 and the argument is equal to π.

modulus and argument of complex numbers in exponential form

The exponential form of a complex number is an easy way to view the modulus and argument.

The modulus is the coefficient of the exponential in front of Euler’s number.

The argument is alongside i in the power of the exponential.

example of finding the modulus and argument of a complex number in exponential form

Modulus and Argument of a Complex Number Calculator

This calculator will calculate the modulus and argument of a complex number.

Simply enter the real part and imaginary part of the complex number in the calculator below.

That is, for any complex number z equals a. plus b i, where a is the real part and b is the imaginary part.

For example, in the complex number z equals the square root of 2 minus i, the real part is the square root of 2 and the imaginary part is -1 because there are -1 lots of i.