How to Write in Logarithmic Form

How to Write in Logarithmic Form: Video Lesson

What is Logarithmic Form?

The logarithmic form is written as log_a(c)=b. It is a rearrangement of the exponential form, a^b=c. Any exponential equation can be written as a logarithm. The logarithmic form is used to calculate an exponent of an equation.

is read as “log base a of c equals b“.

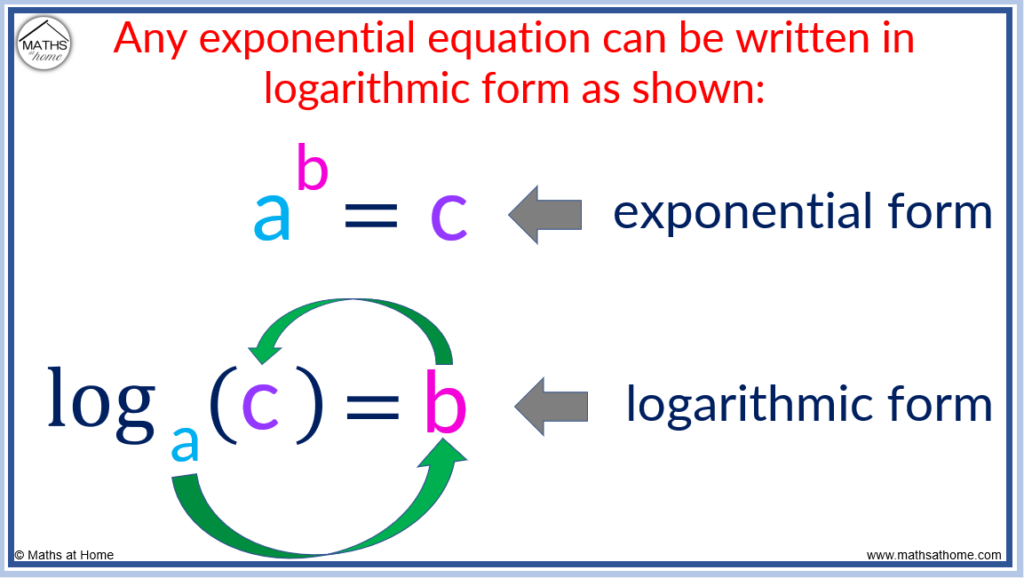
The logarithmic form is simply a rearrangement of an equation written in exponential form. The same numbers are used but they are written in a different order. The word log is written to show that the logarithm function is being used.

An exponential equation contains an exponent (the small number written to the top right of another number).

Equations written in logarithmic form contain three numbers:

• The base of the log is the number written in subscript next to the word ‘log’.
• The number after the equals sign is the exponent.
• The number inside the log before the equals sign is the value of the base raised to the power of the exponent.

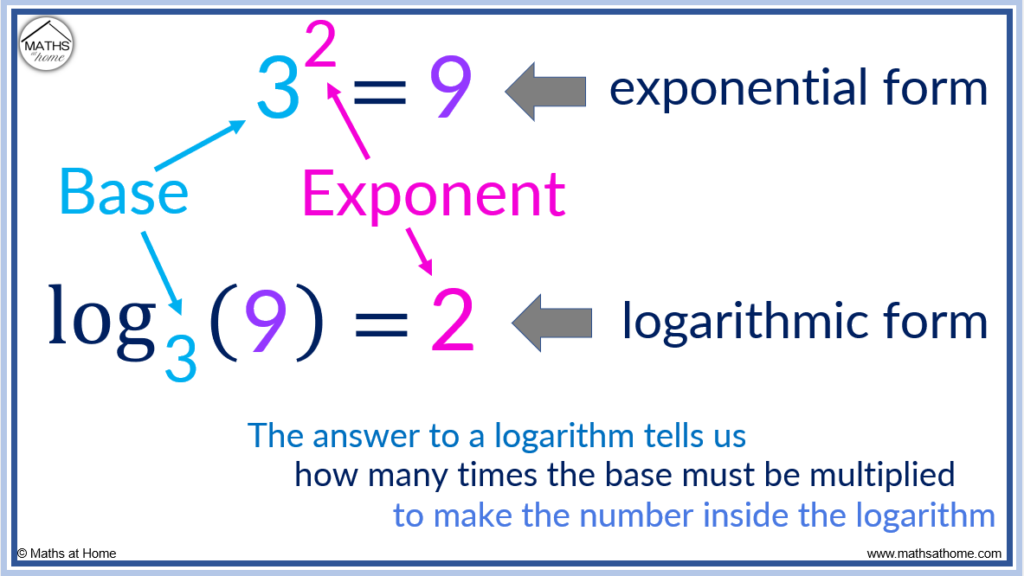
For example, in the exponential equation 3² = 9, the 2 is the exponent.

This can be written in logarithmic form as .

The answer to an equation written in logarithmic form is the exponent.

The 2 is the exponent in the exponential form but it is the answer when written in logarithmic form.

Why do we use the logarithmic form?

The purpose of the logarithmic form is to calculate exponents and solve exponential equations. Logarithms can be used to comprehend the size of large numbers, rearrange equations and solve growth and decay problems.

How are logarithms used in real life?

Here are some examples of where logarithms are used in real life:

• Audio volume. Decibels are measured on a logarithmic scale.
• The pH measure of acidity is a logarithmic scale.
• The Richter scale used to measure earthquakes is on a logarithmic scale.
• Light intensity. The brightness of stars is measured on a logarithmic scale.
• The focal ratio in photography is a logarithmic scale
• The strength of a Wi-Fi signal is measured on a logarithmic scale
• Computer algorithm efficiency is measured on a logarithmic scale
• Radioactive decay and half-life is calculated using logarithms
• Calculating interest rates
• Calculating growth of populations

How to Convert to Logarithmic Form

Any exponential equation of the form a^b=c can be written in logarithmic form using log_a(c)=b. For example, the exponential equation 2³=8 is written as log₂(8)=3 in logarithmic form.

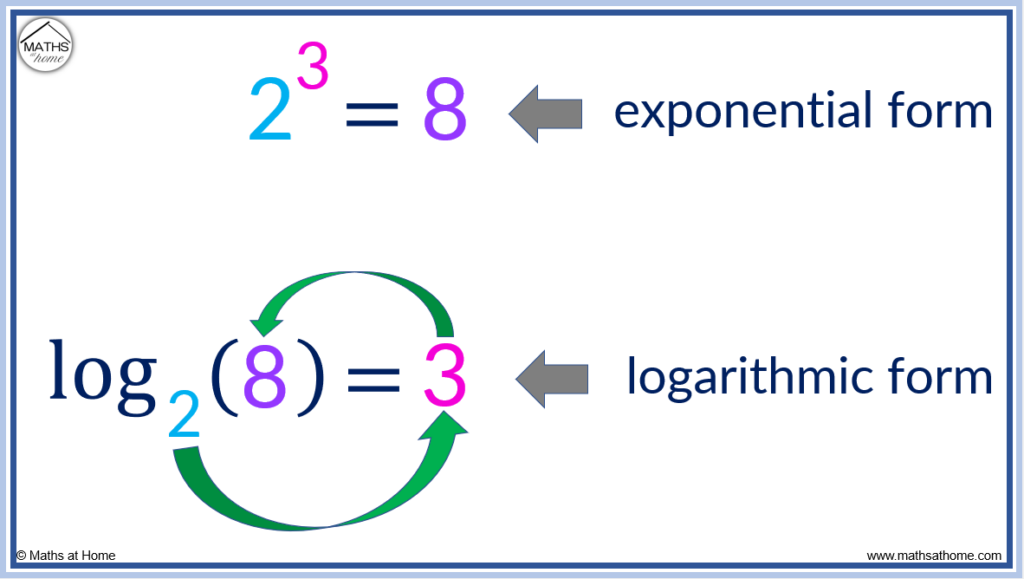
In the example of , , and . Therefore using the formula log_a(c)=b, this can be written in exponential form as .

Here is the exponential equation 3⁴=81. It can be written in logarithmic form as .

The number after the equals sign in logarithmic form is the power that the base of the log is raised to to make the number inside the log. Here 3 is raised to the power 4 to make 81.

If the base of a logarithm is 10, it is not necessary to write the number 10. Whenever a logarithm does not have a base written, it is taken to have base 10.

For example, can be written in logarithmic form as .

Instead of writing the base 10 can be removed and it can be written as

How to Convert Logarithmic Form to Exponential Form

Any equation written in logarithmic form can be written in exponential form by converting log_a(c)=b to a^b=c. For example log₅(25)=2 can be written as 5²=25.

If an equation written in logarithmic form does not have a base written, the base is taken to be equal to 10.

We typically do not write the base of 10.

For example, means .

Since 10²=100, .

The resulting answer to the logarithm is the power that 10 is raised to in order to make 100.

Converting Between Natural Logarithms and the Exponential Form

Euler’s number, e≈2.718. The natural logarithm is a logarithm with base e and is written as ln rather than log. For example ln(x) means log_e(x).

Here are some examples of working with the natural logarithm.

If , then .

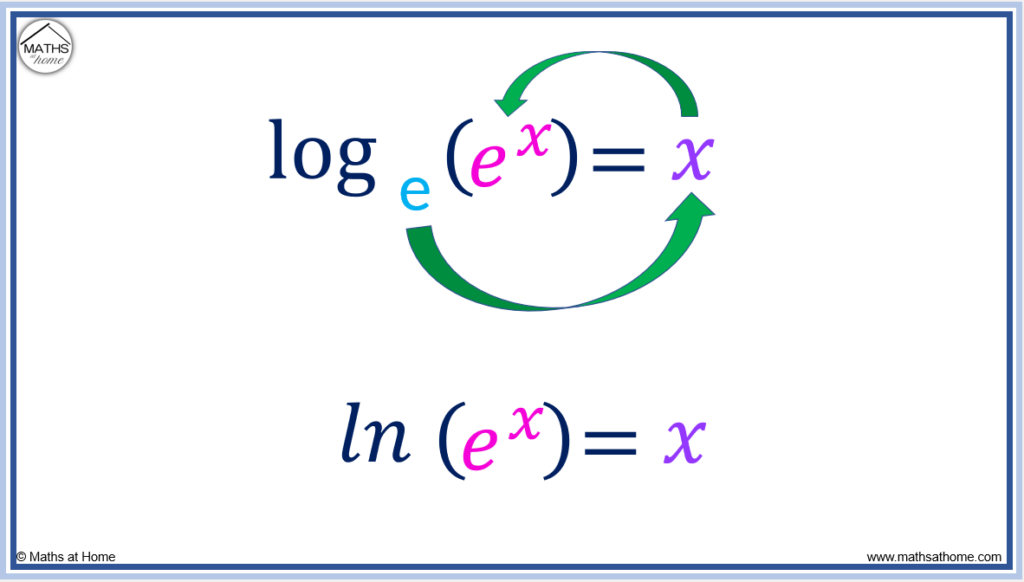
Since e¹=e, then .

If , then .

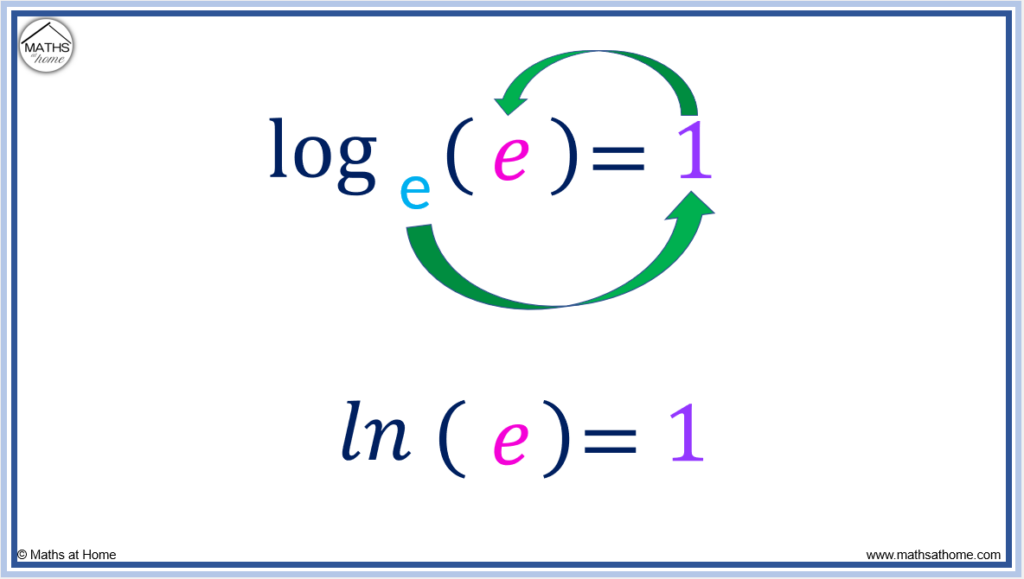
Rules When Using the Logarithmic Form

The following rules apply when writing numbers in logarithmic form:

• If the logarithm base is not written, the base is 10.
• The natural logarithm ln is a logarithm base e.
• No matter what base, the logarithm of 1 is 0. The rule is log_a(1)=0.
• The logarithm of the base number is equal to 1. The rule is log_a(a)=1.
• log_a(0) is undefined.
• Logarithms of negative numbers are undefined.
• The base of a logarithm is never negative, zero or one.

Examples of Writing Equations in Logarithmic Form

Here are some examples of converting exponential equations to the logarithmic form.

Exponential Form	Logarithmic Form
ab=c	loga(c)=b
32=9	log3(9)=2
25=32	log2(32)=5
103=1000	log10(1000)=3 or log(1000)=3
51=5	log5(5)=1
30=1	log3(1)=0
91/2=3	log9(3)=1/2
5-2=1/25	log5(1/25)=-2

Logarithmic Form with Square Roots

Finding the square root of a number is the same as raising it to the power of one half. Therefore √9=3 can be written as 9^1/₂=3. Writing this in logarithmic form, log₉(3)=¹/₂.

Logarithmic Form with Fractions

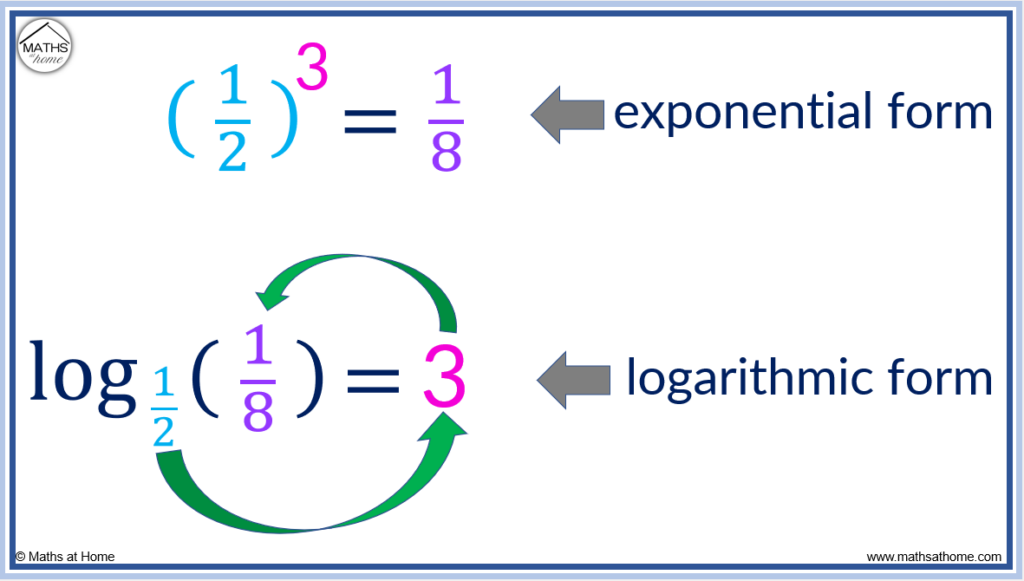
The rule for converting exponential equations, a^b=c, into logarithmic equations, log_a(c)=b, also works for fractions. For example (¹/₂)³=¹/₈ can be written as log_(¹/2)(¹/₈)=3.

Logarithmic Form of Complex Numbers

Any complex number, z=a+bi can be written in form z=re^iθ, where r = √(a²+b²) and θ=tan^-1(b/a)+2πk. The exponential form of a complex number, z=re^iθ can be written in logarithmic form as ln(z)=ln(re^iθ). This can be written as ln(z)=ln(r)+ln(e^iθ), which can be simplified to ln(z)=ln(r)+iθ.