How to Find the Equation of a Tangent Line

How to Find the Equation of a Tangent: Video Lesson

What is a Tangent to a Curve?

A tangent line to a curve is a straight line that just touches the curve at one point. The tangent line has the same gradient as the curve does at this point.

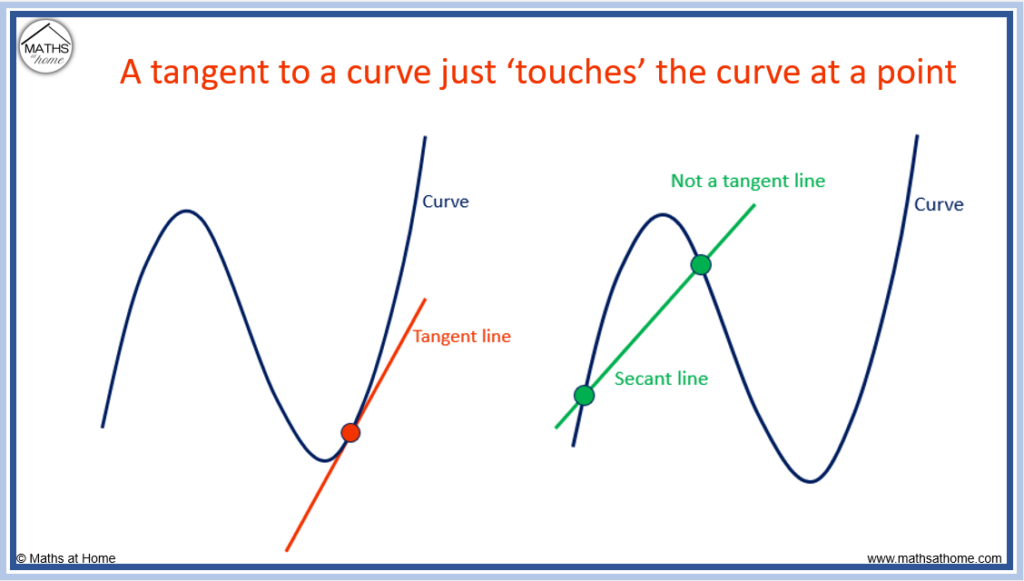
definition of the tangent to a curve

The tangent to the curve above is shown in red.

The tangent to a curve just touches the curve at a given point. It does not pass through the curve at this point, although it can intersect the curve at another location.

A line that passes through two points on a curve is called a secant line. The secant line is shown in green above. This is not a tangent line.

How to Find the Equation of a Tangent using Differentiation

  1. Differentiate the function of the curve.
  2. Substitute the x-coordinate of the given point into this derivative to find the gradient, ‘m’.
  3. Substitute the given coordinates (x,y) along with ‘m’ into ‘y=mx+c’ and then solve to find ‘c’.
  4. Substitute these values of ‘m’ and ‘c’ into ‘y=mx+c’.

Example 1: Equation of the Tangent to a Parabola

For example, find the equation of the tangent to the curve y equals x squared plus 3 x minus 1 at the point (1, 3).

Step 1. Differentiate the function of the curve

If y equals x squared plus 3 x minus 1, then

d y over d x equals 2 x plus 3

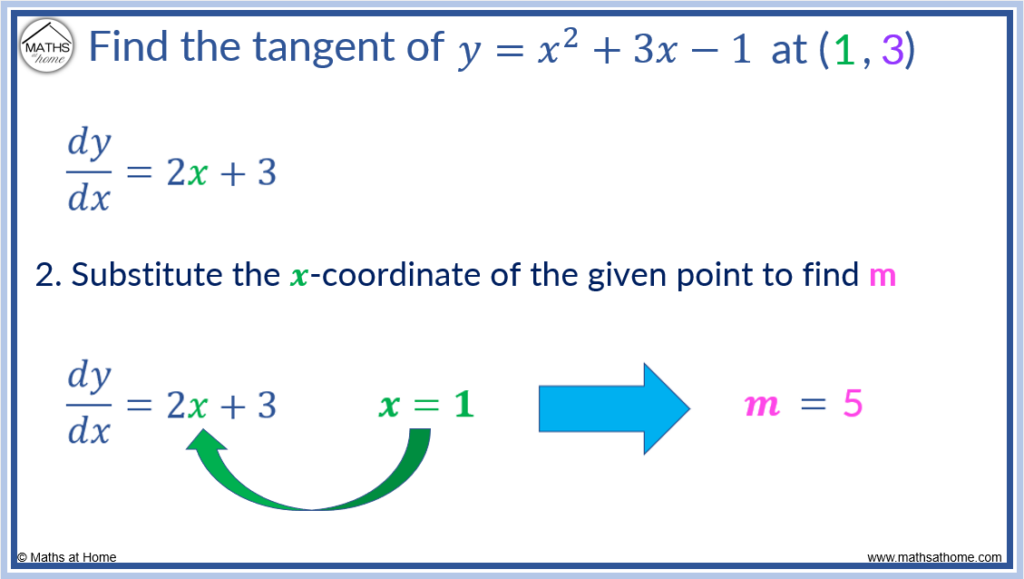
Step 2. Substitute the x-coordinate of the given point into this derivative to find the gradient, ‘m’

The gradient anywhere on the curve is found by the gradient function, d y over d x equals 2 x plus 3.

The tangent is at the point (1, 3).

Here, x=1.

Substituting x=1 into the gradient function d y over d x equals 2 x plus 3, the gradient at this point is found.

2 times 1 plus 3 and so, m=5.

step 2 of finding the equation of a tangent

Step 3. Substitute the given coordinates (x,y) along with ‘m’ into ‘y=mx+c’ and then solve to find ‘c’

Since the tangent is at the point (1, 3), this is where x = 1 and y = 3.

The value of m at this point was previously found to be m = 5.

The tangent is a straight line and so, is represented with the straight line equation y equals m x plus c.

Substituting the values of x = 1, y = 3 and m = 5 into this equation, it becomes 3 equals 5 times 1 plus c.

Solving this equation for c, it is found that c = -2.

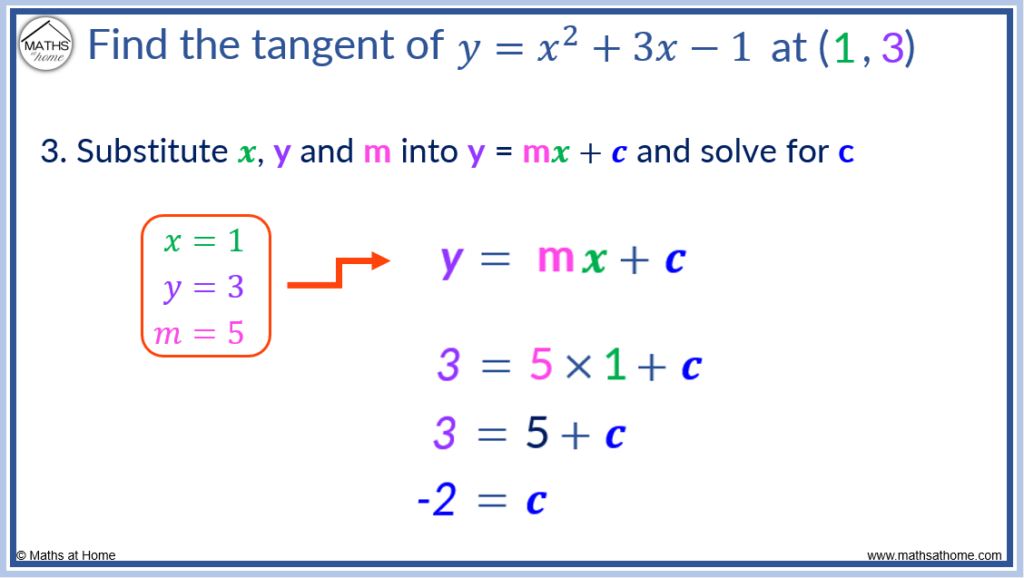
step 3 of finding the equation of a tangent

Step 4. Substitute these values of ‘m’ and ‘c’ into y=mx+c

It has been found that m = 5 and c = -2.

Replacing these values in y equals m x plus c, the equation of the tangent is y equals 5 x minus 2.

how to find the equation of a tangent to a curve

How to Find Where the Tangent Meets the Curve Again

To find where a tangent meets the curve again, first find the equation of the tangent. Then use simultaneous equations to solve both the equation of the tangent and the equation of the curve. Each pair of x and y solutions corresponds to a coordinate (x, y) where the tangent intersects the curve.

For example, find the tangent to y equals the fraction with numerator 2 and denominator x squared at (-1, 2) and find the coordinates where the tangent intersects the curve again.

Firstly, the equation of the tangent is found.

Since y equals 2 x to the negative 2 power, the derivative d y over d x equals negative 4 x to the negative 3 power.

Substituting x equals negative 1 into this derivative, it is found that m equals 4.

Substituting x equals negative 1, y equals 2 and m equals 4 into y equals m x plus c,

2 equals 4 times negative 1 plus c and so, c equals 6.

Therefore since m equals 4 and c equals 6, the equation of the tangent is y equals 4 x plus 6.

how to find the equation of a tangent to a rational function

To find where a tangent to a curve meets the curve again, solve the equation of the tangent and the equation of the curve simultaneously.

Simultaneous equations are used to find the coordinates of intersection of two lines.

The equations y equals 4 x plus 6 and y equals the fraction with numerator 2 and denominator x squared can be solved by setting the equations equal to each other to get 4 x plus 6 equals the fraction with numerator 2 and denominator x squared.

Multiplying each term by x squared, the equation becomes 4 x cubed plus 6 x squared equals 2.

We subtract 2 from both sides to set the equation equal to zero: 4 x cubed plus 6 x squared minus 2 equals 0.

Dividing each term by 2, the equation becomes: 2 x cubed plus 3 x squared minus 1 equals 0.

We already know that one solution is found at x equals negative 1 and so one factor must be open paren x plus 1 close paren.

Dividing 2 x cubed plus 3 x squared minus 1 by open paren x plus 1 close paren using polynomial long division, the result is 2 x squared plus x minus 1, which factorises to open paren x plus 1 close paren times open paren 2 x minus 1 close paren.

Therefore 2 x cubed plus 3 x squared minus 1 equals 0 can be written as open paren x plus 1 close paren squared times open paren 2 x minus 1 close paren equals 0.

finding where the tangent meets the curve again
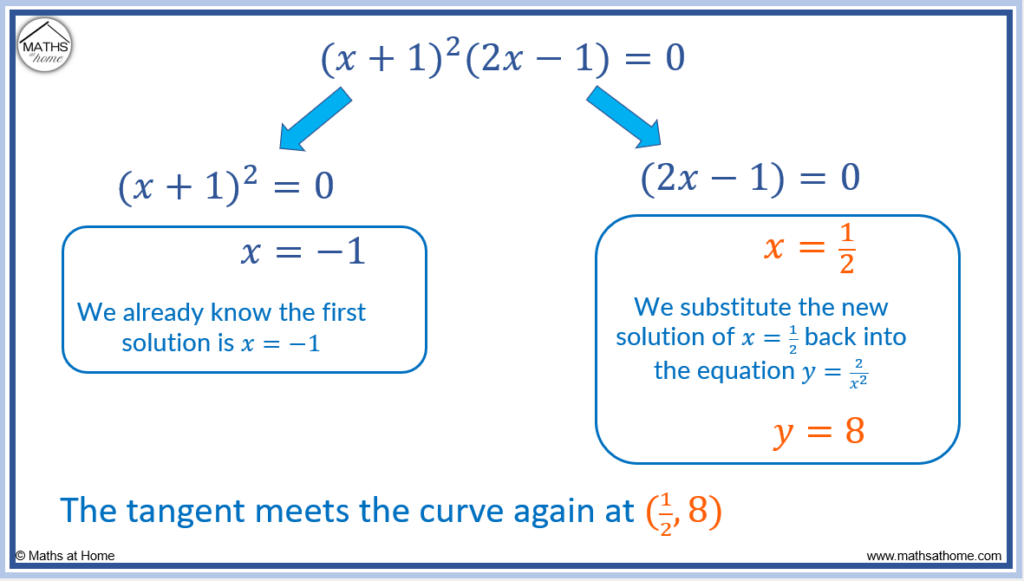
where the tangent intersects the curve again

Therefore either open paren x plus 1 close paren squared equals 0 (which results in the original solution of x equals negative 1, or open paren 2 x minus 1 close paren equals 0, which gives us a new solution of x equals one half.

When x equals one half, the y coordinate can be found by substituting this back into y equals the fraction with numerator 2 and denominator x squared to get y equals 8.

Therefore the tangent intersects the curve again at open paren one half comma 8 close paren.

Formula for the Equation of a Tangent

The equation of the tangent to y=f(x) at the point x=a is given by the formula: y=f'(a)(x-a)+f(a).

The formula for the equation of tangent is derived from g of r a. d i e n t equals the fraction with numerator y sub 1 minus y sub 2 and denominator x sub 1 minus x sub 2.

The gradient of the tangent when x equals a. is equal to the derivative at the point x equals a., which is given byf prime of a..

y sub 1 and x sub 1 can be taken as any y and x points on the tangent line.

y sub 2 is equal to f of a. and x sub 2 is equal to a..

The gradient equation becomes f prime of a. equals the fraction with numerator y minus f of a. and denominator x minus a. which can be rearranged to give y equals f prime of a. times open paren x minus a. close paren plus f of a..

formula for the equation of a tangent

The equation of a tangent to y equals f of x at the point x equals a. is found using the formula: y equals f prime of a. times open paren x minus a. close paren plus f of a..

For example, the find the equation of the tangent of f of x equals x cubed minus 2 x at (0, 0).

The x-coordinate of the point (0, 0) is 0 and so, a = 0.

Differentiating the function, f prime of x equals 3 x squared minus 2.

f of a. is found by substituting x = 0 into f of x equals x cubed minus 2 x.

Therefore, f of a. equals 0 cubed minus 2 times 0 and so f of a. equals 0.

f prime of a. is found by substituting x = 0 into f prime of x equals 3 x squared minus 2.

Therefore f prime of a. equals 3 times 0 squared minus 2 and so f prime of a. equals negative 2.

using the formula for the equation of a tangent

To find the equation of the tangent, substitute a. equals 0, f of a. equals 0 and f prime of a. equals negative 2 into y equals f prime of a. times open paren x minus a. close paren plus f of a..

This becomes y equals negative 2 times open paren x minus 0 close paren plus 0 which simplifies to y equals negative 2 x.

Equation of a Tangent to a Circle

To find the equation of a tangent to a circle:
  1. Find the gradient from the centre of the circle to the tangent point.
  2. Calculate the negative reciprocal of this gradient to find ‘m’.
  3. Substitute the x and y coordinate values along with ‘m’ into ‘y=mx+c’ and solve for c.
  4. Put the values of ‘m’ and ‘c’ back into ‘y=mx+c’.

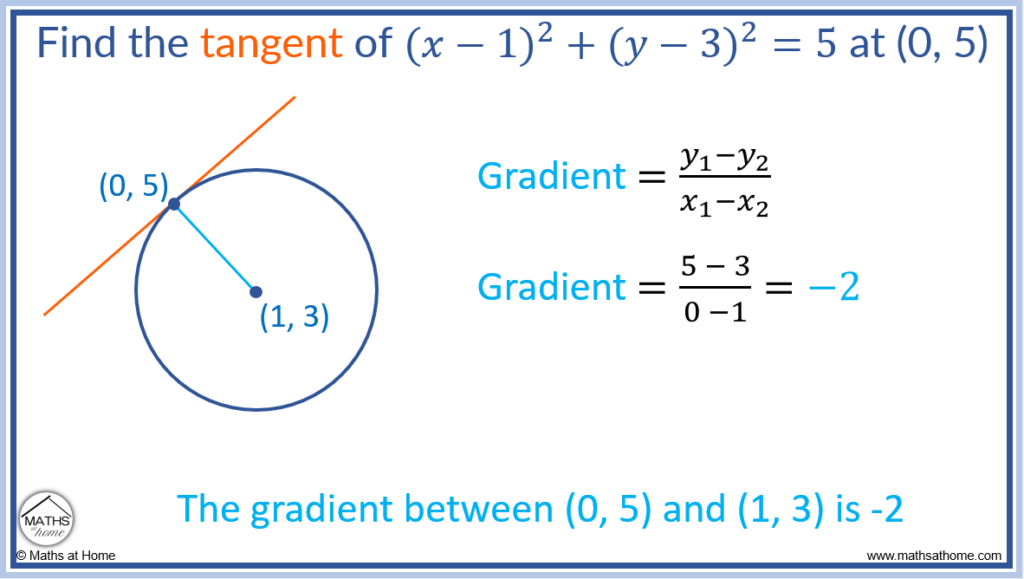
For example, find the tangent to the circle open paren x minus 1 close paren squared plus open paren y minus 3 close paren squared equals 5 at the point (0, 5).

Step 1. Find the gradient from the centre of the circle to the tangent point

The centre of the circle is at (1, 3). The tangent point is at (0, 5).

The gradient is found using the fraction with numerator y sub 1 minus y sub 2 and denominator x sub 1 minus x sub 2.

Evaluating this for the two points, the fraction with numerator 5 minus 3 and denominator 0 minus 1 which equals -2. The gradient between the centre and the point given is -2.

step 1 of finding a tangent to a circle

Step 2. Calculate the negative reciprocal of this gradient to find ‘m’

The gradient of the tangent to a circle is perpendicular to the gradient from the centre to the same point.

The gradient of a line is found by the negative reciprocal of the gradient of the line perpendicular to it.

To calculate the negative reciprocal of a number, calculate -1 divided by that number.

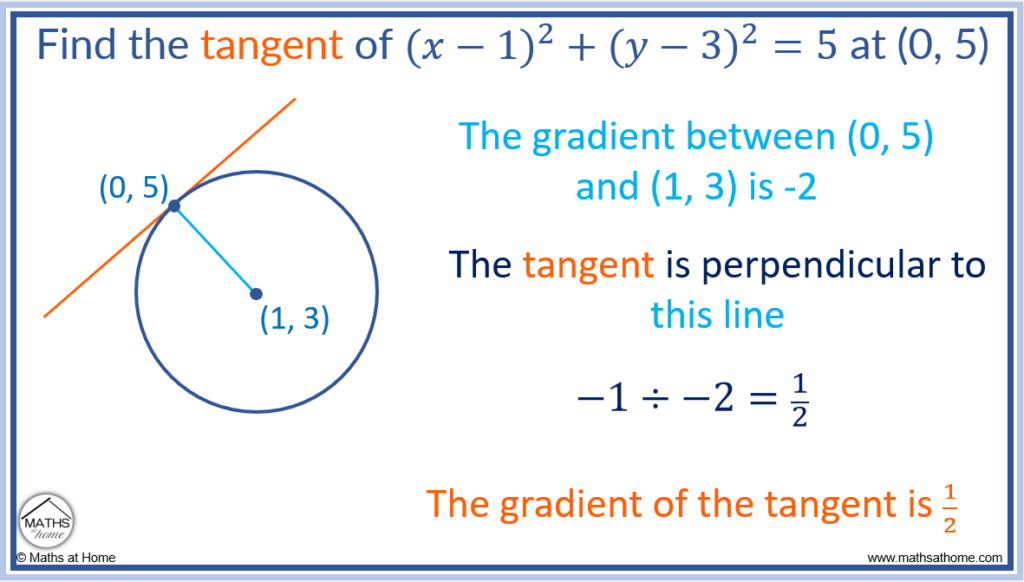
step 2 of finding a tangent to a circle

negative 1 divided by negative 2 equals one halfand so the gradient of the tangent to the circle at this point is one half.

The value of ‘m’ for the tangent line to the circle is one half.

Step 3. Substitute the x and y coordinate values along with ‘m’ into ‘y=mx+c’ and solve for c

The tangent is at the point (0, 5) so we substitute x equals 0, y equals 5 and m = one half into the straight line equation y equals m x plus c.

This results in 5 equals one half times 0 plus c and so, c equals 5.

step 3 of finding a tangent to a circle

Step 4. Put the values of ‘m’ and ‘c’ back into ‘y=mx+c’

It was found that m = one half and c = 5. Therefore the equation of the tangent to the circle is y equals one half x plus 5

Equation of a Tangent to a Square Root Function

The tangent of a square root function can be found by differentiating it and substituting in the x-coordinate to find the gradient. This can be done by writing the function inside the square root as raised to the power of one half. This can then be differentiated using the chain rule.

For example, find the equation of a tangent to the function f of x equals the square root of x minus 2 at the point (6, 2).

We can use the formula for the equation of a tangent: y equals f prime of a. times open paren x minus a. close paren plus f of a..

Step 1. Differentiate the function

f of x equals the square root of x minus 2 and this can be written as f of x equals open paren x minus 2 close paren raised to the one half power.

This can be differentiated using the chain rule to get f prime of x equals one half times open paren x minus 2 close paren raised to the negative one half power.

Step 2. Find f'(a) and f(a)

‘a’ is the x-coordinate of the point at which the tangent meets the curve. In this example, a. equals 6.

f of a. is found by substituting the value of ‘a’ into the f of x equals open paren x minus 2 close paren raised to the one half power equation.

open paren 6 minus 2 close paren raised to the one half power equals 2 and so, f of a. equals 2.

f prime of a. is found by substituting the value of ‘a’ into the f prime of x equals one half times open paren x minus 2 close paren raised to the negative one half power equation.

one half times open paren 6 minus 2 close paren raised to the negative one half power equals one fourth and so, f prime of a. equals one fourth.

Step 3. Substitute the values of f(a), f'(a) and a into the tangent formula

y equals f prime of a. times open paren x minus a. close paren plus f of a. and so, the equation of the tangent becomes y equals one fourth times open paren x minus 6 close paren plus 2.

This simplifies to y equals one fourth x plus one half.

Multiplying each term by 4, this can also be written as 4 y equals x plus 2 or rearranged as 4 y minus x equals 2.

Equation of a Tangent to y=sin(x)

Find the equation of the tangent to f of x equals sine x at the point open paren pi over 4 comma the fraction with numerator the square root of 2 and denominator 2 close paren.

Step 1. Differentiate the function

f of x equals sine x and f prime of x equals cosine x.

Step 2. Find f'(a) and f(a)

‘a’ is the x-coordinate of the point at which the tangent meets the curve. In this example, a. equals pi over 4.

f of a. is found by substituting x equals pi over 4 into f of x equals sine x.

the sine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2 and so, f of a. equals the fraction with numerator the square root of 2 and denominator 2.

f prime of a. is found by substituting x equals pi over 4 into f prime of x equals cosine x.

the cosine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2 and so, f prime of a. equals the fraction with numerator the square root of 2 and denominator 2.

Step 3. Substitute the values of f(a), f'(a) and a into the tangent formula

y equals f prime of a. times open paren x minus a. close paren plus f of a. and so, the equation of the tangent becomes y equals the fraction with numerator the square root of 2 and denominator 2 times open paren x minus pi over 4 close paren plus the fraction with numerator the square root of 2 and denominator 2.

This expands to give y equals the fraction with numerator the square root of 2 and denominator 2 x minus the square root of 2 pi over 8 plus the fraction with numerator the square root of 2 and denominator 2.

Multiplying each term by 8, this becomes: 8 y equals 4 the square root of 2 x minus the square root of 2 pi plus 4 the square root of 2.

Factorising the 4 the square root of 2, this becomes 1 lines Line 1: 8 y equals 4 the square root of 2 times open paren x plus 1 minus pi over 4 close paren.

Dividing by 8 both sides, 1 lines Line 1: y equals the fraction with numerator the square root of 2 and denominator 2 times open paren x plus 1 minus pi over 4 close paren.

Equation of a Tangent with Implicit Differentiation

To find the equation of a tangent using implicit differentiation:
  1. Differentiate the function implicitly.
  2. Evaluate the derivative using the x and y coordinate values to find ‘m’.
  3. Substitute the x and y coordinates along with this value of m into (y-y1)=m(x-x1).

For example, find the equation of the tangent to y to the fifth power minus x cubed equals 5 at the point (3, 2).

Step 1. Differentiate the function implicitly

When differentiating implicitly, differentiate each x term like usual but remember to include a d y over d x after each y term.

y to the fifth power minus x cubed equals 5 differentiates implicitly to 5 y to the fourth power d y over d x minus 3 x squared equals 0.

Step 2. Evaluate the derivative using the x and y coordinate values to find ‘m’

At the point (3, 2), x equals 3 and y equals 2.

Substituting these into 5 y to the fourth power d y over d x minus 3 x squared equals 0, we get 80 d y over d x minus 27 equals 0.

Therefore, rearranging for d y over d x, we get d y over d x equals 27 over 80.

This is the value of m in our straight line equation.

Step 3. Substitute the x and y coordinates along with this value of m into (y-y1)=m(x-x1)

The equation of a straight line can be given as open paren y minus y sub 1 close paren equals m times open paren x minus x sub 1 close paren.

x equals 3, y equals 2 and m equals 27 over 80.

Therefore the equation becomes open paren y minus 2 close paren equals 27 over 80 times open paren x minus 3 close paren.

This can be expanded to get y minus 2 equals 27 over 80 x minus 81 over 80.

Adding 2 to both sides and simplifying, y equals 27 over 80 x plus 79 over 80. This can be written as y equals 1 over 80 times open paren 27 x plus 79 close paren.

How to Find the Equation of a Tangent from an External Point

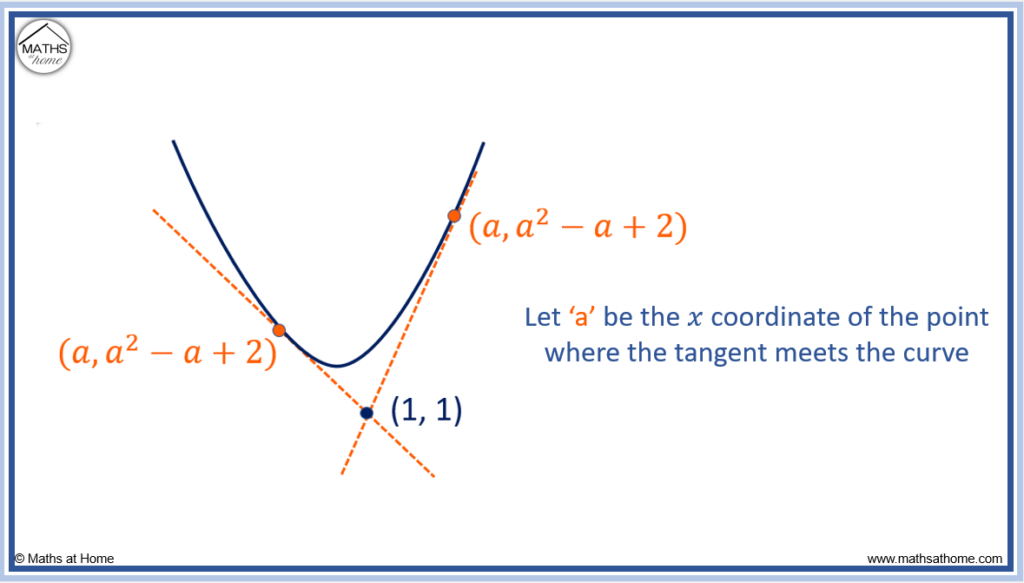
To find the tangent to a curve from an external point, first find the point ‘a’ on the curve where the tangent is. To do this, differentiate the function and set this equal to the change in y over the change in x from the external point to point ‘a’ on the curve. Solve this for ‘a’. Once the location of ‘a’ has been found, find the equation of the tangent in the usual manner.

For example, find the equation of the tangents to the curve y equals x squared minus x plus 2 passing through the point (1, 1).

There are two possible tangents to the curve from this point.

The locations at which the tangent meets the curve will be given the x coordinate of x equals a. and the y coordinate of y equals a. squared minus a. plus 2.

finding a tangent from an external point

Step 1. Differentiate the function

If y equals x squared minus x plus 2, then d y over d x equals 2 x minus 1.

Step 2. Set the derivative at point a equal to the gradient between the external point and the curve

At the point where the tangent meets the curve, x equals a. and so, d y over d x equals 2 a. minus 1.

The gradient between two points is the fraction with numerator y sub 1 minus y sub 2 and denominator x sub 1 minus x sub 2.

open paren x sub 1 comma y sub 1 close paren will be taken as the point on the curve open paren a. comma a. squared minus a. plus 2 close paren.

open paren x sub 2 comma y sub 2 close paren will be taken as the external point open paren 1 comma 1 close paren.

Therefore the fraction with numerator y sub 1 minus y sub 2 and denominator x sub 1 minus x sub 2 becomes the fraction with numerator open paren a. squared minus a. plus 2 close paren minus 1 and denominator a. minus 1. This simplifies to the fraction with numerator a. squared minus a. plus 1 and denominator a. minus 1.

The value of d y over d x for the tangent must be equal to this gradient.

Therefore 2 a. minus 1 equals the fraction with numerator a. squared minus a. plus 1 and denominator a. minus 1.

Step 3. Solve this equation to find the location of the tangent at ‘a’

Multiplying by a-1, the equation above becomes open paren 2 a. minus 1 close paren times open paren a. minus 1 close paren equals a. squared minus a. plus 1.

Expanding brackets: 2 a. squared minus 3 a. plus 1 equals a. squared minus a. plus 1.

Since this is a quadratic, we rearrange to make the right hand side of the equation equal to zero: a. squared minus 2 a. equals 0 .

Factorising: a. times open paren a. minus 2 close paren equals 0 and so, a. equals 0 or a. equals 2.

Therefore, the tangent meets the curve at x equals 0 or x equals 2.

Substitute these values back into y equals x squared minus x plus 2 to get (0, 2) and (2, 4) respectively.

Step 4. Work out the tangent equation for each point

Considering the tangent at the first point, (0, 2).

We know that d y over d x equals 2 x minus 1 and so, d y over d x equals negative 1. Therefore m = -1.

x equals 0, y equals 2 and m equals negative 1.

Therefore y equals m x plus c becomes 2 equals negative 1 times 0 plus c and c equals 2.

The equation of the first tangent is y equals negative x plus 2.

Considering the tangent at the second point, (2, 4).

d y over d x equals 2 x minus 1 and so, d y over d x equals 3 and m equals 3.

x equals 2, y equals 4 and m equals 3.

Therefore y equals m x plus c becomes 4 equals 3 times 2 plus c and therefore c equals negative 2.

The equation of the second tangent is y equals 3 x minus 2.