How to Find the Diagonal of a Rectangle Video Lesson:
How to Find the Diagonal of a Rectangle Using the Pythagorean Theorem
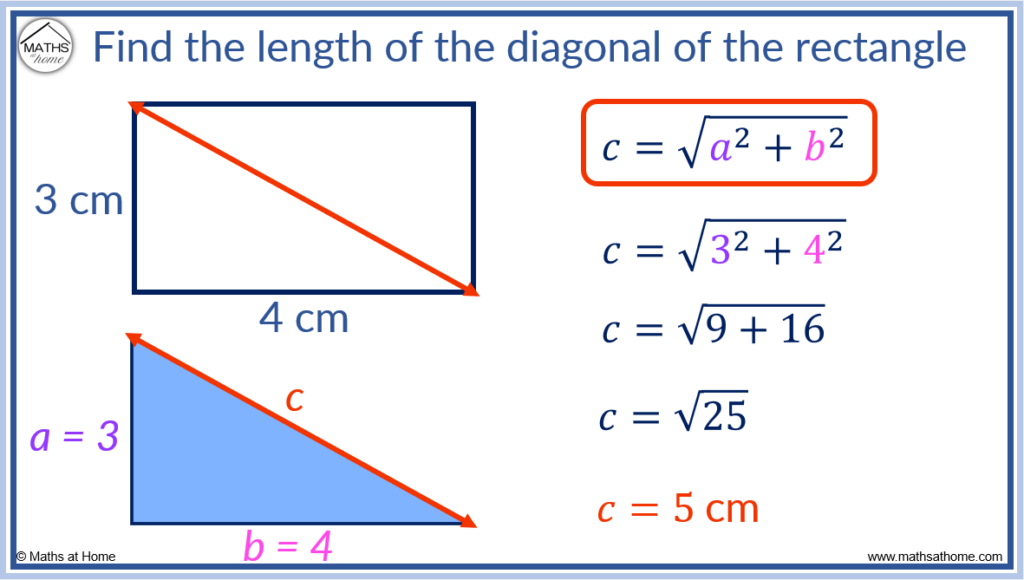
To find the diagonal of a rectangle using the Pythagorean Theorem, use the formula d = √(l² + w²), where l is the length and w is the width of the rectangle. For example, the diagonal of a rectangle of length 4cm and width 3cm is given by d = √(4² + 3²). Evaluating this, d = √25 and therefore the diagonal is 5cm long.
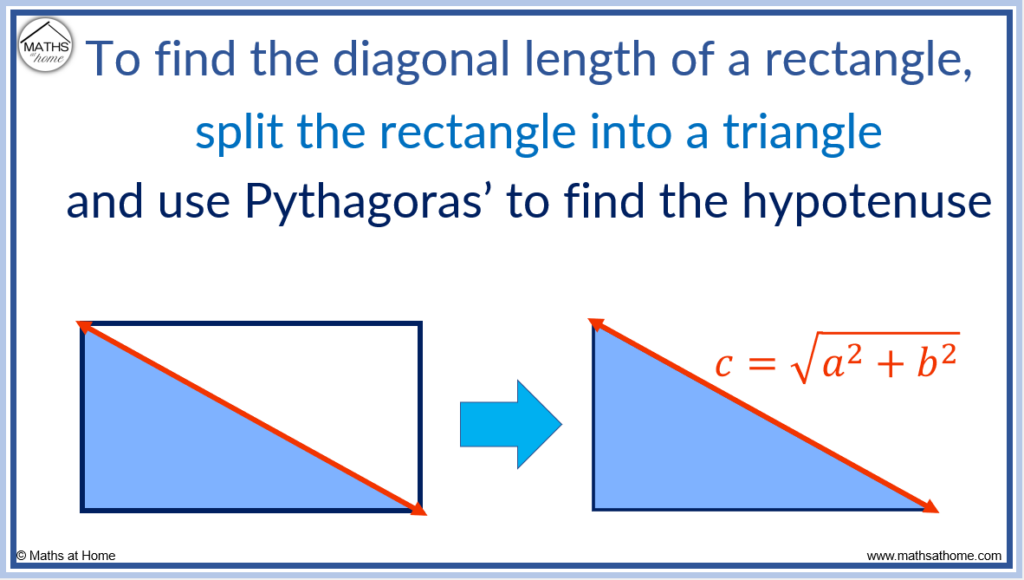
The diagonals of a rectangle are equal in length and divide the rectangle into two congruent triangles. This means that the rectangle is divided into two right-angled triangles from which Pythagoras’ Theorem can be used
Given the length and width of a rectangle, the diagonal is found by squaring these values, adding them and then finding the square root of this. The diagonal is the hypotenuse of the triangle formed by dividing the rectangle in two.
Formula to Find the Diagonal of a Rectangle
The formula to find the diagonal of a rectangle is d = √(l² + w²), where l is the length and w is the width of the rectangle. For example, the diagonal of a rectangle of length 6m and width 2m is given by d = √(6² + 2²). Evaluating this, d = √40 and therefore the diagonal is approximately 6.32m long.
The formula for the length of the diagonal of a rectangle
Example 1:
A rectangle has length of 6m and a width of 2m.
Therefore and
.
Substituting these values into the formula , we obtain
.
This becomes and evaluating this, the diagonal is approximately 6.32m long.


Example 2:
Which rectangle has the longest diagonal?
The first rectangle has length of 8 cm and width of 4 cm.
which equals
. Evaluating this, the diagonal is approximately 8.94 cm long.
The second rectangle has a length of 7 cm and a width of 5 cm.
, which equals
. Evaluating this, the diagonal is approximately 8.60 cm long.
Therefore the first rectangle has the longest diagonal.

Diagonal of a Rectangle Calculator
The diagonal of a rectangle calculator will calculate the length of the diagonal of a rectangle when the length and width of the rectangle are known.
Simply enter the length and width of the rectangle into the calculator to calculate the diagonal length.
How to Find the Diagonal of a Square
To find the diagonal length of a square, use the formula d=√2×a, where a is the side length of the square. For example, the diagonal length of a square 10cm long is d=√2×10. Evaluating this, the diagonal length is 14.1cm.
Formula for the diagonal length of a square with side lengths ‘a’

The formula for the diagonal length of a square is derived from Pythagoras’ Theorem for the length of the diagonal of a rectangle.
For a rectangle, the diagonal length is given by , where l is the length and w is the width of the rectangle.
For a square, the length and width are equal. If the length and width are both equal to ‘a’, then becomes
.
This simplifies to .
This can be written as , which equals
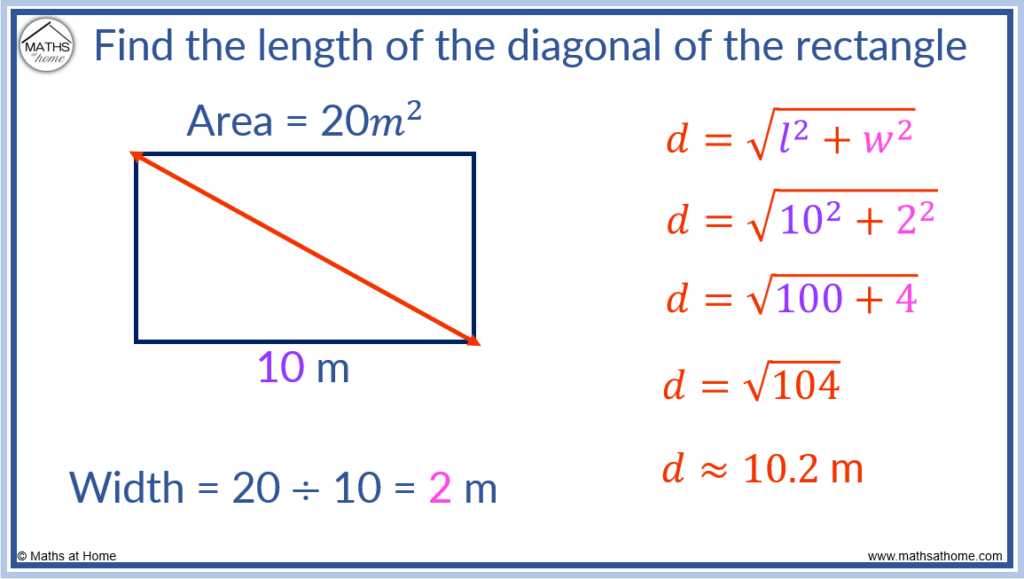
How to Find the Diagonal of a Rectangle Given the Area
If the area and one side of a rectangle are known, divide the area by the known side to find the other side. These two sides are the length (l) and the width (w). Then use the Pythagorean Theorem, d = √(l² + w²), to calculate the diagonal of the rectangle.
Example 1:
For example, find the diagonal of a rectangle with area 20 m2 and length of 10 m.
First divide the area by the length to find the width.
and so, the width is 2 m long.
Now we can use to find the diagonal, given that l=10 and w=2.
which becomes
, which equals 10.2 m.
Example 2:
Find the area of a rectangle given that the diagonal is 5cm long and the length is 4cm long.
To find the area of the rectangle, use the formula .
Find we need to find the height using Pythagoras’ Theorem.
To find the width, knowing the diagonal, use the formula .
Since the diagonal is 5 cm and the length is 4 cm, this becomes , which equals
.
The width is 3 cm. This is the height of the rectangle.
.

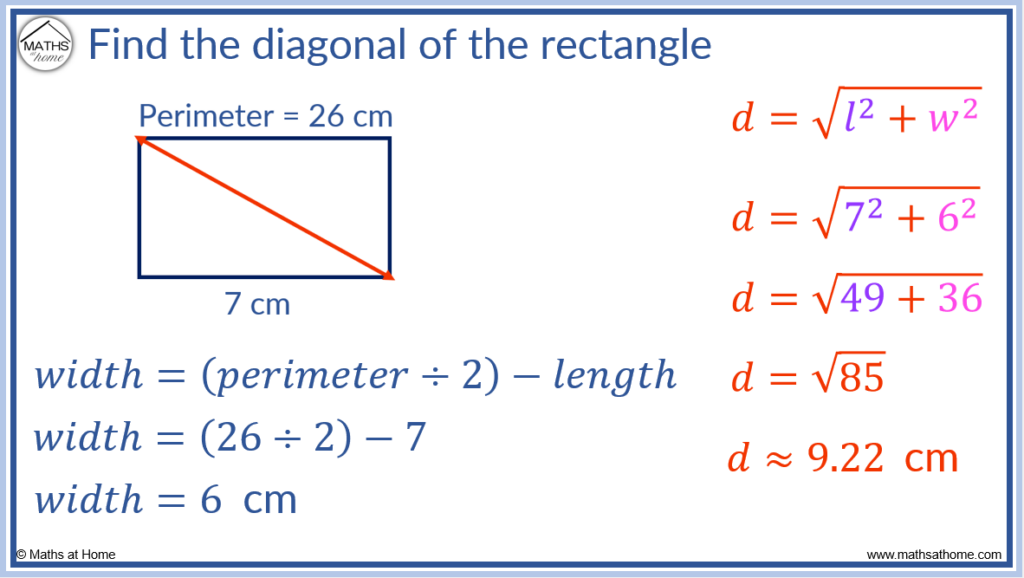
How to Find the Diagonal of a Rectangle Given the Perimeter
If the perimeter and side length of a rectangle are known, subtract the known side length from half of the perimeter to find the other side length. These two sides are the length (l) and the width (w). Then use the Pythagorean Theorem, d = √(l² + w²), to calculate the diagonal of the rectangle.
Example 1:
Find the diagonal of a rectangle with perimeter 26 cm and length of 7 cm.
First, find the width of the rectangle by subtracting the length from half of the perimeter.
Half of the perimeter is 13 cm. 13 – 7 = 6 and so, the width of the rectangle is 6 cm.
Now that the length = 7 and the width = 6, becomes
.
This equals and so, the diagonal length is approximately 9.22 cm.