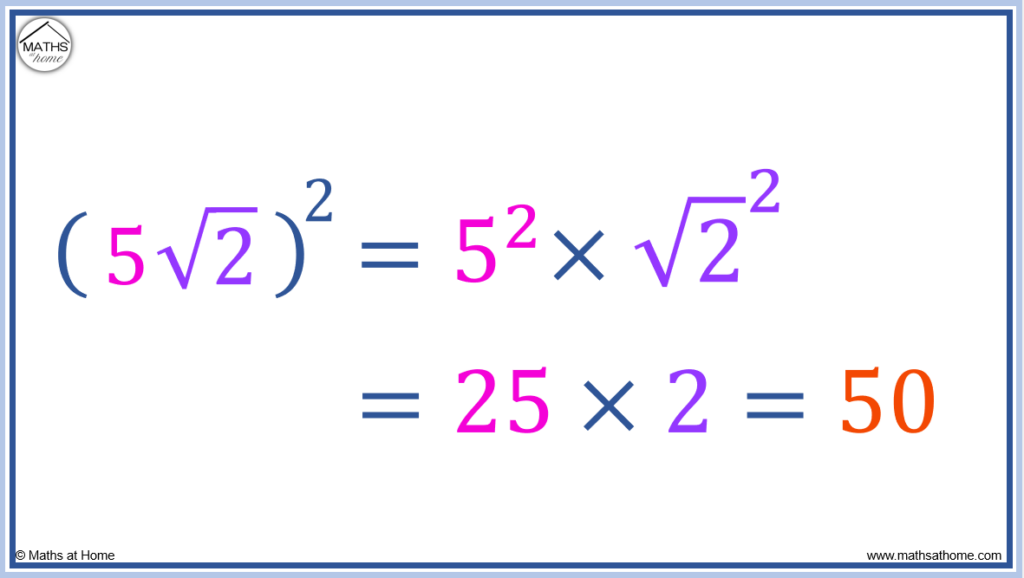How to Simplify Surds

Simplifying Surds Video Lessons:

What is a Surd?

A surd is a number written as a root that cannot be simplified to a whole number. A surd is irrational, which means that if it were written as a decimal it would go on forever. For example, √2 is a surd but √4 is not because √4 is equal to 2.

Put simply, if a number under a square root is not a perfect square number then it is a surd. If the answer to any root contains decimal numbers, then it will be a surd.

The square numbers are obtained by multiplying a number by itself.

The first few square numbers are 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100.

Finding the square root of these numbers will not result in a surd.

If the result of a square root is a whole number, it is not a surd.

Surds are formed from any root, including cube roots, fourth roots etc. If they do not have an integer answer then they are a surd.

For example, ³√8 is not a surd because it equals 2. However ³√5 is a surd because it is not equal to a whole number and is instead equal to the irrational number starting with 1.70997594668…

What is Simplified Surd Form?

Larger surds can often be simplified so that the number inside the root is made smaller. A surd is written in simplified form when the number inside the root has no square factors. For example, √8 can be written as √4×√2, which equals 2√2.

Common square factors include 4, 9, 16, 25 and 36.

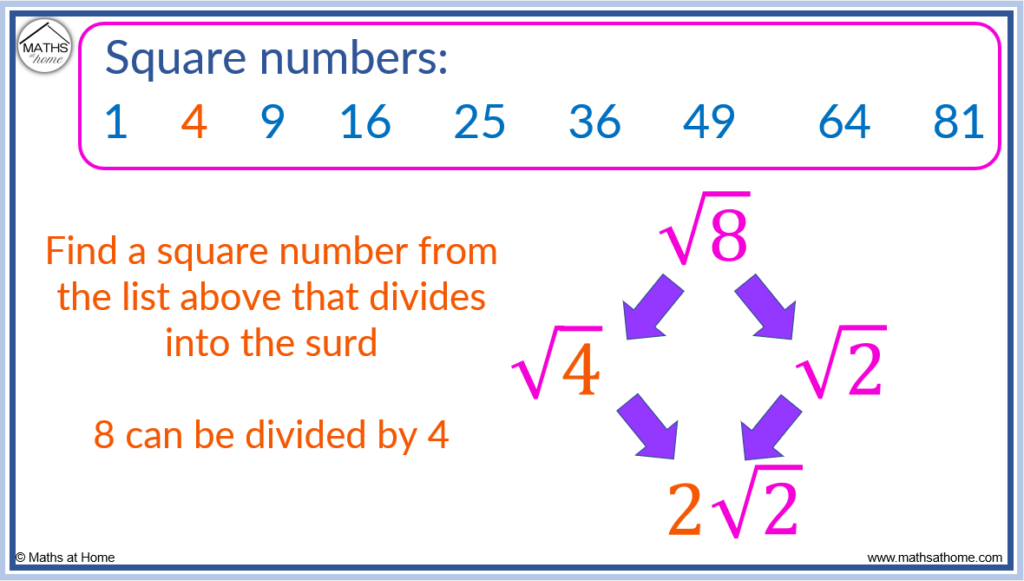
For example, √8 is a surd that can be simplified.

and so, .

The square root of 4 is just 2 and so, becomes or .

When surds are simplified, the simplified surd is written as a whole number next to a number within a root.

How to Simplify Surds

To simplify a surd:

1. Find the largest square number that divides exactly into the surd.
2. Rewrite the surd as the product of this square number and another number.
3. Find the square root of the square number.

Example 1: Simplify the surd √12.

1. Find the largest square number that divides exactly into the surd

The first few square numbers are 1, 4, 9, 16, 25, 36 and 49

The largest square number that divides into 12 is 4.

2. Rewrite the surd as the product of this square number and another number

and so, which can be written as .

3. Find the square root of the square number

The square root of 4 is 2.

Therefore can be written as .

as a simplified surd is .

Example 2: Simplify the surd √75.

1. Find the largest square number that divides exactly into the surd

The first few square numbers are 1, 4, 9, 16, 25, 36 and 49

The largest square number that divides into 75 is 25.

2. Rewrite the surd as the product of this square number and another number

and so, , which can be written as .

3. Find the square root of the square number

The square root of 25 is 5.

Therefore can be written as .

as a simplified surd is .

Simplifying Surds Examples

Here are some examples of simplifying surds:

Surd	Square factor	Simplified Surd
√8	√4√2	2√2
√12	√4√3	2√3
√20	√4√5	2√5
√18	√9√2	3√2
√27	√9√3	3√3
√45	√9√5	3√5
√32	√16√2	4√2
√48	√16√3	4√3
√80	√16√5	4√5
√50	√25√2	5√2
√75	√25√3	5√3
√125	√25√5	5√5
√72	√36√2	6√2
√98	√49√2	7√2
√200	√100√2	10√2
√300	√100√3	10√3

Rules for Simplifying Surds

Here are 6 rules for simplifying surds:

1.

For example, can be written as . This can be written as , which can simplify to .

2.

For example,

3.

For example, .

4. and so, .

This is known as rationalising the denominator. Rationalising the denominator removes the surd from the denominator of the fraction.

For example, and so, .

5.

This is another technique for rationalising the denominator.

For example, . This simplifies to , which simplifies to .

6.

This is another technique for rationalising the denominator.

For example, . This simplifies to .

laws of surds

Simplifying Surds with Addition and Subtraction

To simplify surds using addition and subtraction, first fully simplify each individual surd. Then only add and subtract surds that have the same number under the root. For example, 2√3 + 4√3 = 6√3. If the surds do not have the same number under the root, they cannot be added.

Simply add or subtract the number in front of each surd.

In the case of , we simply count how many ‘s there are.

Since 10 – 7 = 7, we obtain .

Simplifying and then adding surds

Simplify surds first where necessary in order to find like surds that can be added.

For example: Simplify .

18 is different to 50 and so, these are not like surds.

Simplifying, can be written as , which equals .

simplifies to , which equals .

Now both surds are simplified, the number under the square root is the same. Both surds have .

.

Here are some examples of adding and subtracting surds:

Example	Simplified surds	Answer
√8 + √18	2√2 + 3√2 =	5√2
√12 + √27	2√3 + 3√3 =	5√3
√75 + √12	5√3 + 2√3 =	7√3
√80 + √45	4√5 + 3√5 =	7√5
√24 + √600	2√6 + 10√6 =	12√6

How to Simplify Surds with Different Roots

To add or subtract surds, they must have the same root. Only add the surds with the same root together. Do not add or subtract surds with different roots. For example, 2√3+5√2+3√3-2√2 = 5√3+3√2.

Considering the terms containing : we obtain .

Considering the terms containing: we obtain .

How to Simplify Surds with Multiplication

To multiply surds, multiply the numbers in front of the roots together. Then multiply the numbers inside the roots together, keeping the answer inside a root. For example, 2√5 × 3√2 = 6√10.

Here are the rules for multiplying surds:

• 

For example, .

• 

For example, .

• 

For example, .

• 

For example, .

How to Divide Surds

To divide surds, divide the numbers in front of the roots. Then divide the numbers inside the roots, keeping the answer inside a root. For example 10√6 ÷ 2√3 = 5√2.

How to Simplify Surds with a Number in Front

When adding or subtracting surds with numbers in front, simply add or subtract these numbers, whilst keeping the number inside the square root the same. When multiplying or dividing surds with numbers in front, multiply or divide the numbers in front and the number inside the square root.

For example:

• – The remained the same, we just add 2 + 4 to get 6.
• – The remained the same, we just subtract 10 – 3 to get 7.
• – We multiply 2 × 3 = 6 and 5 × 2 = 10, writing the 10 inside the square root.
• – We divide 10 ÷ 2 = 5 and 6 ÷ 3 = 2, writing the 2 inside the square root.

How to Simplify Surds in Fractions

To simplify surds written in a fraction, first simplify the numerator and denominator separately. Then cancel any surds or whole numbers that are in common to both the numerator and denominator.

Example 1

Simplify .

First simplify the numerator and denominator separately.

Simplifying the numerator:

Simplifying the denominator: .

The fraction of becomes .

Cancel any surds or whole numbers that are in common to both the numerator and denominator.

In , both the numerator and denominator contain .

Dividing both the numerator and denominator by ,

becomes .

Therefore, simplifies to .

Example 2

Simplify .

First simplify the numerator and denominator separately.

Simplifying the numerator: .

Simplifying the denominator: .

The fraction of becomes .

Cancel any surds or whole numbers that are in common to both the numerator and denominator.

contains a 4 on the numerator and the denominator. Divide both the numerator and denominator by 4.

becomes .

Therefore simplifies to .

By multiplying the denominator and numerator by , this can be written as .

Rationalising the Denominator of a Surd

To rationalise the denominator of a surd, multiply the numerator and denominator by the surd on the denominator. For example, ²/_√3 rationalised is ²/_√3 × ^√3/_√3 = ^2√3/₃. For a denominator with two terms, multiply by the conjugate of the denominator.

Rationalising the denominator means to rewrite a fraction so that its denominator is a whole number instead of a surd. A surd is an irrational number and writing the denominator as a whole number makes it rational.

Example 1:

Rationalise the denominator of .

The surd has a denominator of and so, we multiply the numerator and denominator by .

.

Example 2:

Rationalise the denominator of .

The denominator has two terms. Therefore we multiply the numerator and denominator by the conjugate.

The conjugate is the same as the denominator but the subtraction sign is replaced with an addition sign.

The conjugate of is .

Rationalising the denominator, .

Expanding the denominator we get, . This simplifies to .

Therefore the fraction becomes , which simplifies to or .

How to Simplify Surds in Brackets

To simplify surds in brackets, expand the bracket by multiplying every term inside the bracket by the number outside the bracket. To multiply a surd by a whole number, simply write the whole number in front of the surd. To multiply two surds, multiply the numbers inside the square roots.

Example 1:

Simplify .

We multiply both the 3 and the by .

Therefore, .

Example 2:

Expand and simplify .

Multiply each term in the bracket by each term in the bracket.

expanded is which simplifies to .

How to Simplify Surds with Powers

To simplify surds that are raised to a power, firstly write the surd as an index. Then multiply this index by the power. For example, (√2)⁴ = (2^1/₂)⁴, which simplifies to 2², which equals 4.

Square roots can be written as the power of ¹/₂.

Cube roots can be written as the power of ¹/₃.

Roots can be written as indices in the following ways:

Root	Power
√a	a1/2
3√a	a1/3
4√a	a1/4
5√a	a1/5
n√a	a1/n

Example 1:

In the example of , the square root is rewritten as a power of one half.

becomes .

The powers are then multiplied to simplify.

and so, , which equals 4.

Example 2:

Simplify .

The cube root of 5 can be written as 5 to the power of one third.

.

Multiplying the indices, .

Therefore .

Example 3:

Simplify .

In this example, both the 5 and the are raised to the power of 2.

Therefore,