How to Find the Area Between Two Curves

Area Between Two Curves: Video Lesson

How to Find the Area Between Two Curves

To find the area between two curves, the formula is A=∫[f(x)-g(x)]dx, where f(x) is the upper curve and g(x) is the lower curve. The limits of integration are the values of x read from the x-axis for which the area is found between.

A r e a. equals the integral from a. to b of f of x minus g of x d x

f of x is the equation of the upper curve. This curve must be above the other curve.

g of x is the equation of the lower curve. This curve must be below the other curve.

A r e a. equals the integral from a. to b of u p p e r c u r v e minus l o w e r c u r v e d x

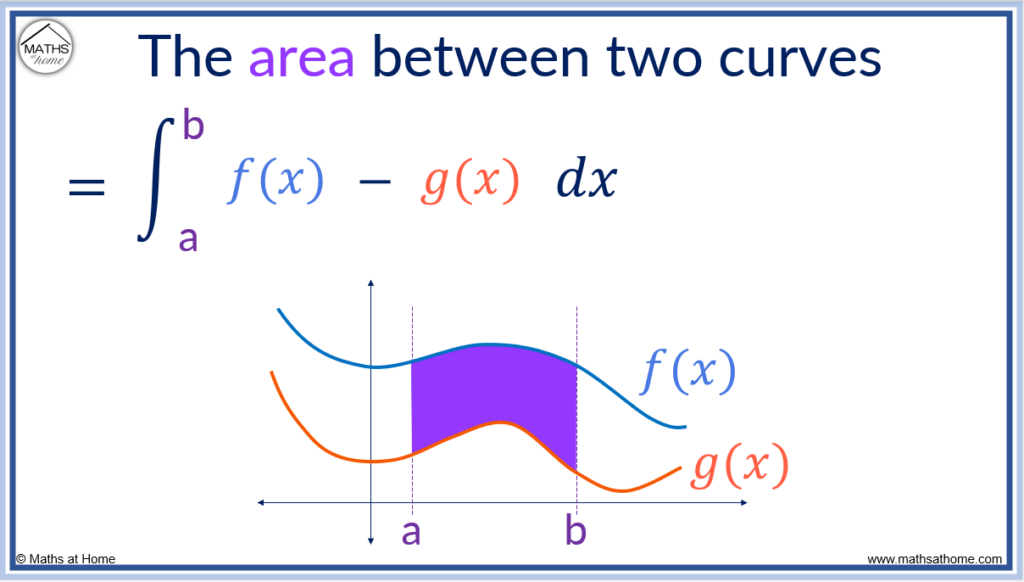
formula for the area between two curves

The formula for the area between two curves is derived through integrating each curve to obtain the area below it. Subtracting the integral of the lower curve from the integral of the upper curve provides the area between the two curves.

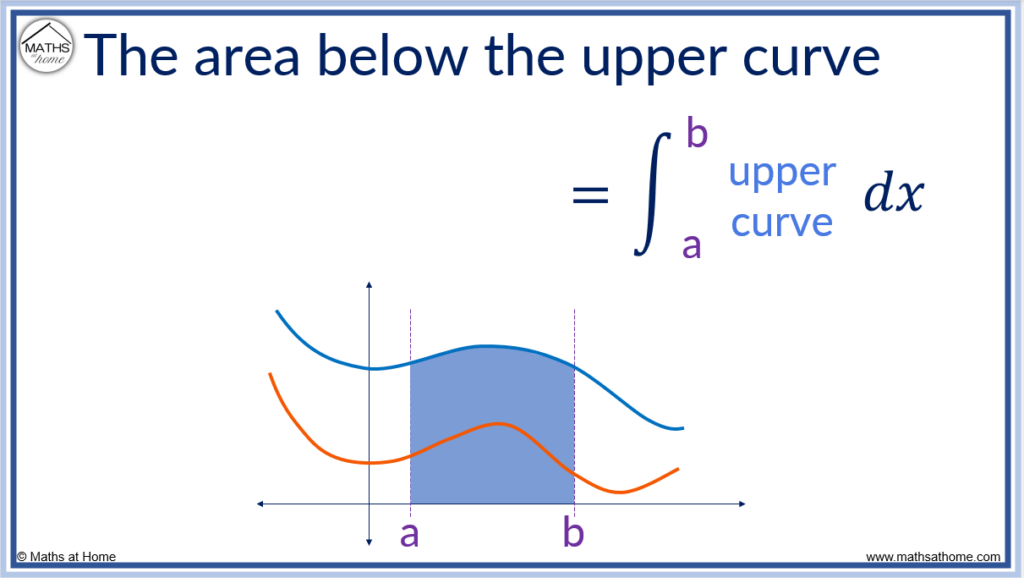
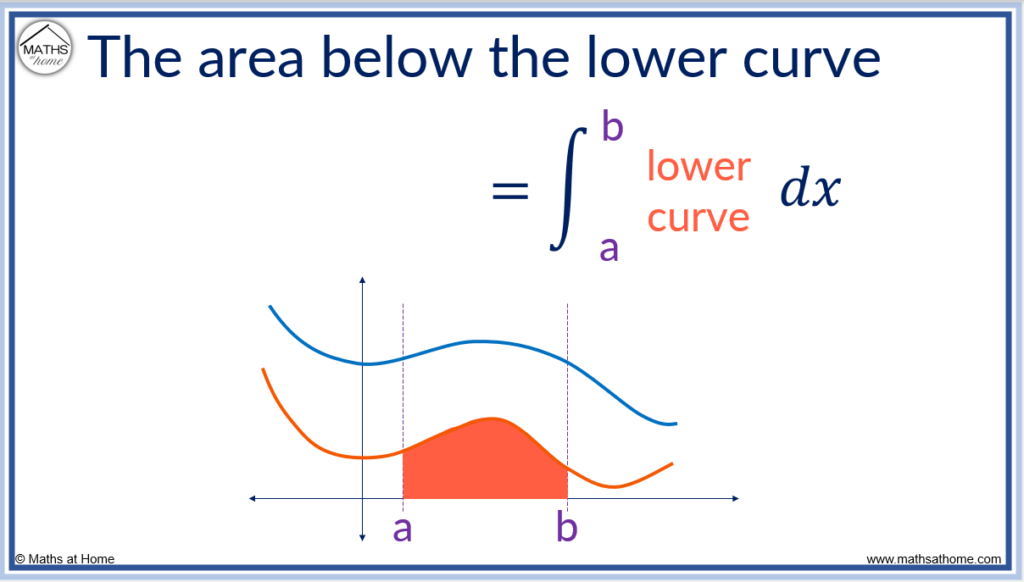
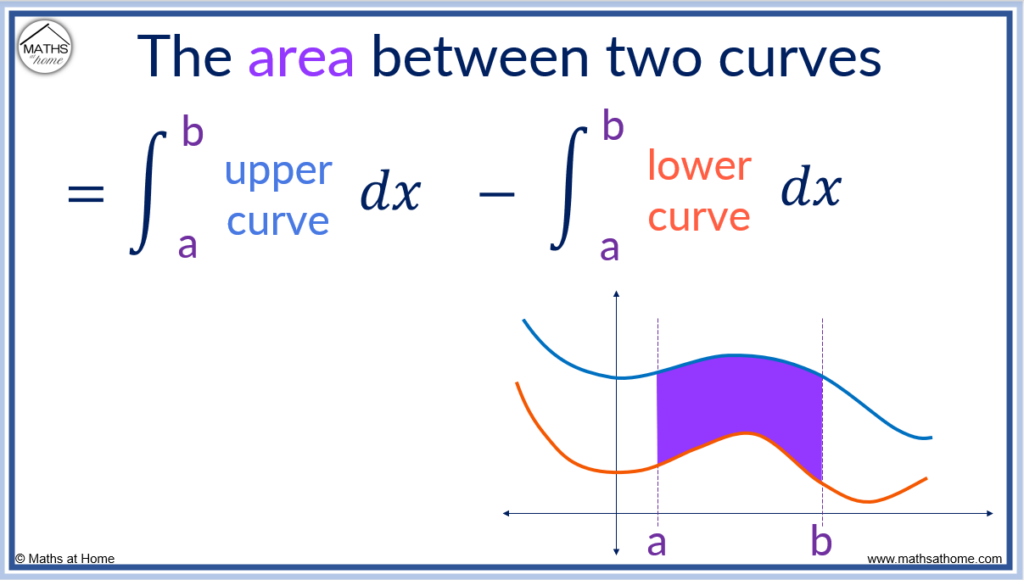
The steps to finding the area between two curves are:

  1. Find the 𝑥-coordinates of intersection of the curves
  2. Integrate the upper curve minus the lower curve within each region
  3. The limits of integration are the 𝑥-coordinates at the start and end of each region
  4. Add the areas of the individual regions to find the total area

For example, find the area between the two curves y equals x cubed minus 6 x plus 3 and y equals x squared plus 3.

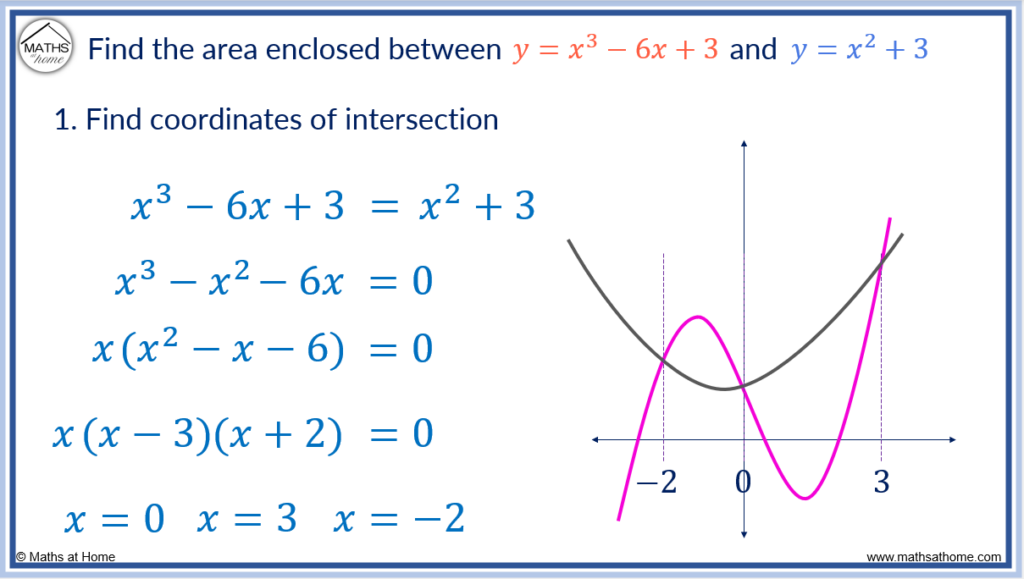
Step 1. Find the 𝑥–coordinates of intersection of the curves

To find the coordinates of intersection, solve the two equations simultaneously.

Setting the equations equal to each other and rearranging the right hand side of the equals sign to equal zero we get:

x cubed minus 6 x plus 3 equals x squared plus 3

x cubed minus x squared minus 6 x equals 0

We can solve this equation by factoring out 𝑥:

x times open paren x squared minus x minus 6 close paren equals 0

Factorising the resulting quadratic:

x times open paren x minus 3 close paren times open paren x plus 2 close paren equals 0

Therefore x equals 0 comma x equals 3 o r x equals negative 2

step 1 of finding the area between two curves

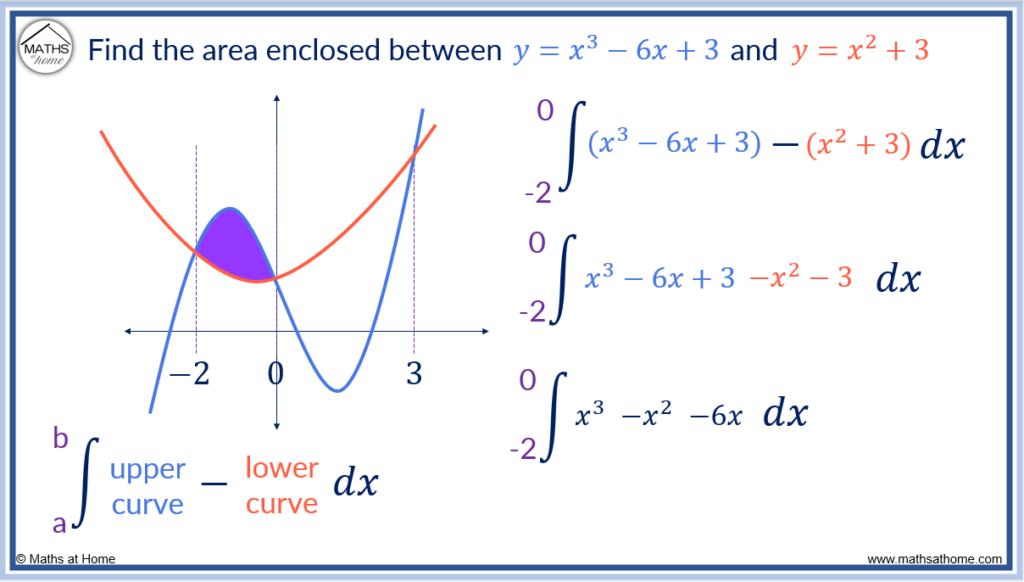
Step 2. Integrate the upper curve minus the lower curve in each region

In the first region, the limits of integration are from -2 to 0. These are the first two points of intersection found in step 1.

The upper curve is simply the curve that is above the other curve in the region chosen. The lower curve is the one that is below the other one.

In this region, the upper curve is y equals x cubed minus 6 x plus 3 and the lower curve is y equals x squared plus 3.

We subtract the lower curve equation from the upper curve equation to get:

x cubed minus x squared minus 6 x

Step 3. The limits of integration are the 𝑥-coordinates at the start and end of each region

The region is found between the 𝑥 coordinates of -2 and 0. The area is found by integrating between the limits of -2 and 0.

step 2 of finding the area between two curves

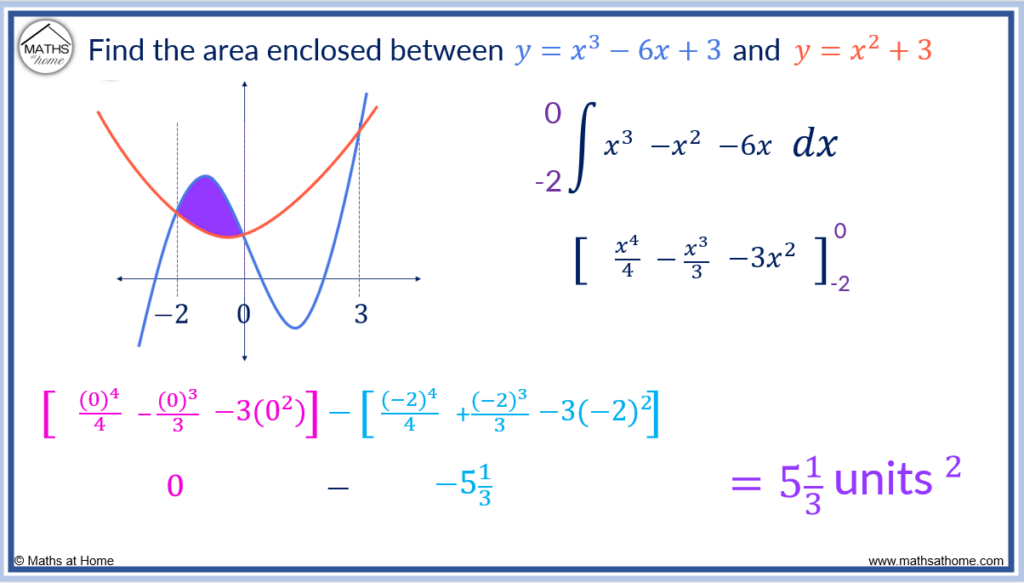
Integrating the integral from negative 2 to 0 of x cubed minus x squared minus 6 x d x we get open bracket the fraction with numerator x to the fourth power and denominator 4 minus the fraction with numerator x cubed and denominator 3 minus 3 x squared close bracket sub negative 2 to the 0 power.

Evaluate the integral to get 0 minus negative 5 and one third equals 5 and one third.

This is the area of the first region.

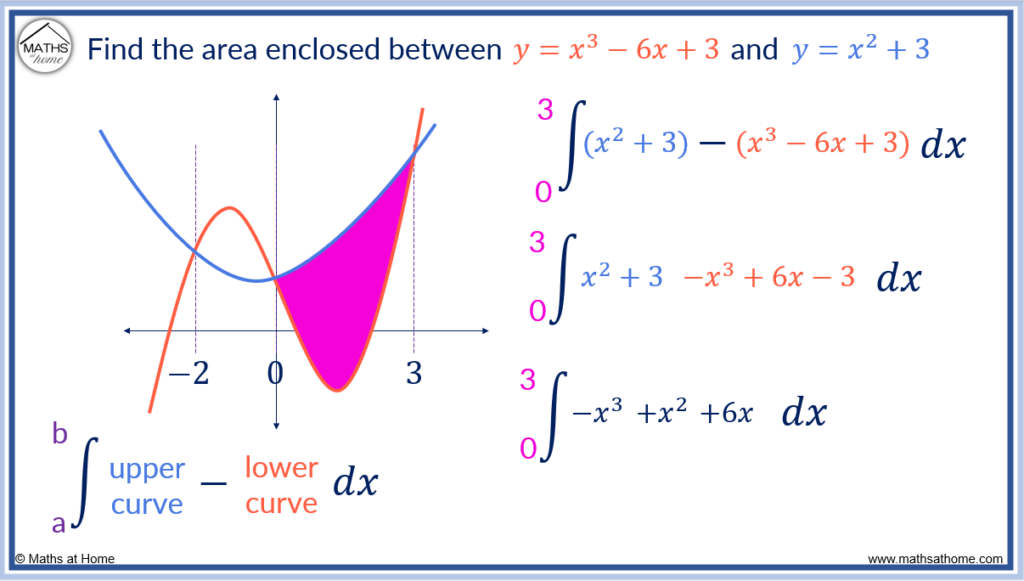
step 2 of finding the area between curves using integration

Now the area of the second region is found between the two curves bound between 0 and 3.

In this region, the upper curve has the equation y equals x squared plus 3 and the lower curve is y equals x cubed minus 6 x plus 3.

The area between two curves is given by the integral of the upper curve subtract the lower curve.

x squared plus 3 minus open paren x cubed minus 6 x plus 3 close paren simplifies to negative x cubed plus x squared plus 6 x.

The area is found bythe integral from 0 to 3 of negative x cubed plus x squared plus 6 x d x.

step 2 of finding the area between curves

the integral from 0 to 3 of negative x cubed plus x squared plus 6 x d x becomes open bracket negative the fraction with numerator x to the fourth power and denominator 4 plus the fraction with numerator x cubed and denominator 3 plus 3 x squared close bracket sub sub 0 cubed.

Evaluating this integral, 15 and three fourths minus 0 equals 15 and three fourths.

This is the area of the second region between the two curves.

step 2 of finding the area between two curves

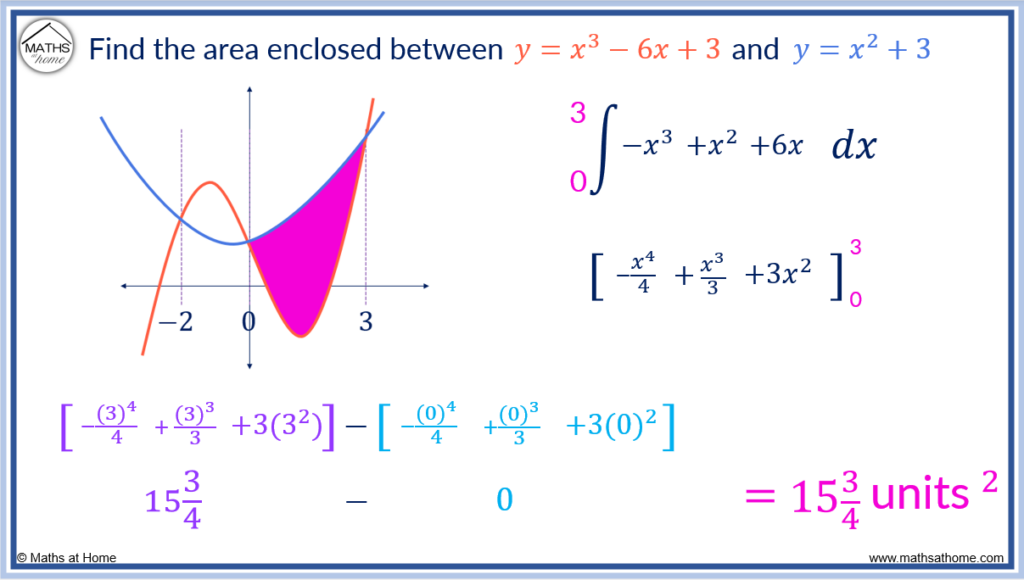
Step 4. Add the areas of the individual regions to find the total area

There are two regions between the two curves in this example.

Adding the two areas gives the total area between the two curves.

5 and one third plus 15 and three fourths equals 21 and 1 over 12 u n i t s squared

how to find the area between two curves

The area between two curves is always positive and will never be negative. If a negative area is obtained, an error must have been made in the calculation. This is true for the total area and the individual areas bound in each region.

Common mistakes made when finding the area between two curves are:

  • Not identifying the upper and lower curve correctly for each individual region
  • Finding incorrect limits of integration due to an error when solving the simultaneous equations
  • Using the limits of integration in the wrong order
  • Numerical mistakes particularly with subtracting negative numbers

Area Between Two Curves Problems and Solutions

Finding the Area Between Two Curves Below the x-axis

It does not matter if the area between two curves is below the x-axis. Simply identify the upper curve as the function that is above the lower curve. Subtract the equation of the lower curve from the equation of the upper curve and then integrate.

For example, find the area between the curves y equals x squared minus 3 x plus 2 and y equals 2 x minus 2.

Step 1. Find the 𝑥–coordinates of intersection of the curves

The two equations can be solved simultaneously by setting the two equations equal to each other, rearranging for zero and then factorising.

x squared minus 3 x plus 2 equals 2 x minus 2 becomes x squared minus 5 x plus 4 equals 0, which factorises to open paren x minus 4 close paren times open paren x minus 1 close paren equals 0.

Therefore, the coordinates of intersection are 𝑥=4 and 𝑥=1.

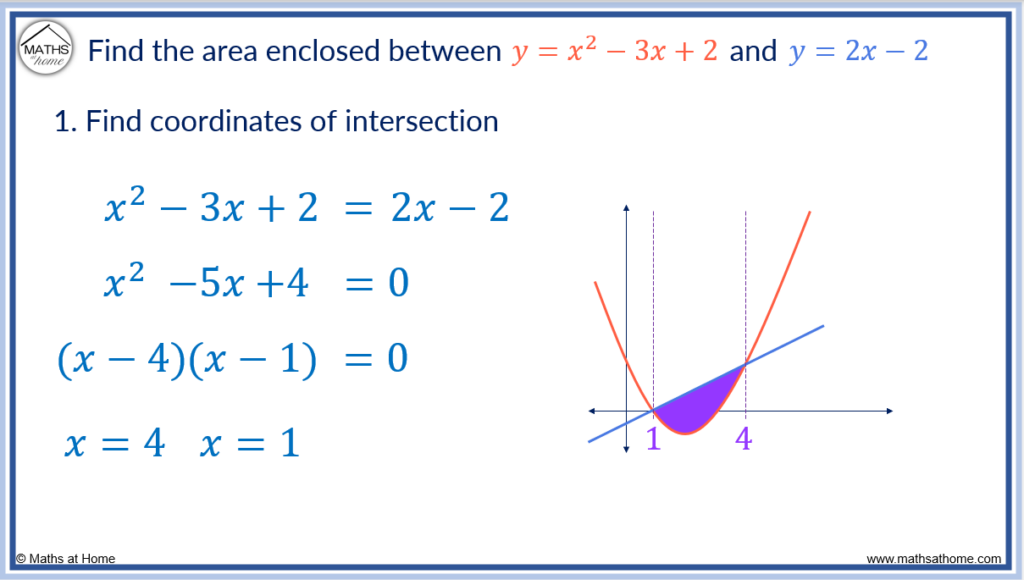
area between two curves example of area below the x axis

Step 2. Integrate the upper curve minus the lower curve in each region

There is only one region in this example. The linear equation is above the quadratic equation at all times in this region.

Therefore the upper curve is y equals 2 x minus 2 and the lower curve is y equals x squared minus 3 x plus 2.

Subtracting the lower curve from the upper curve, the following expression is obtained:

negative x squared plus 5 x minus 4

Step 3. The limits of integration are the 𝑥-coordinates at the start and end of each region

The limits of integration are 1 and 4.

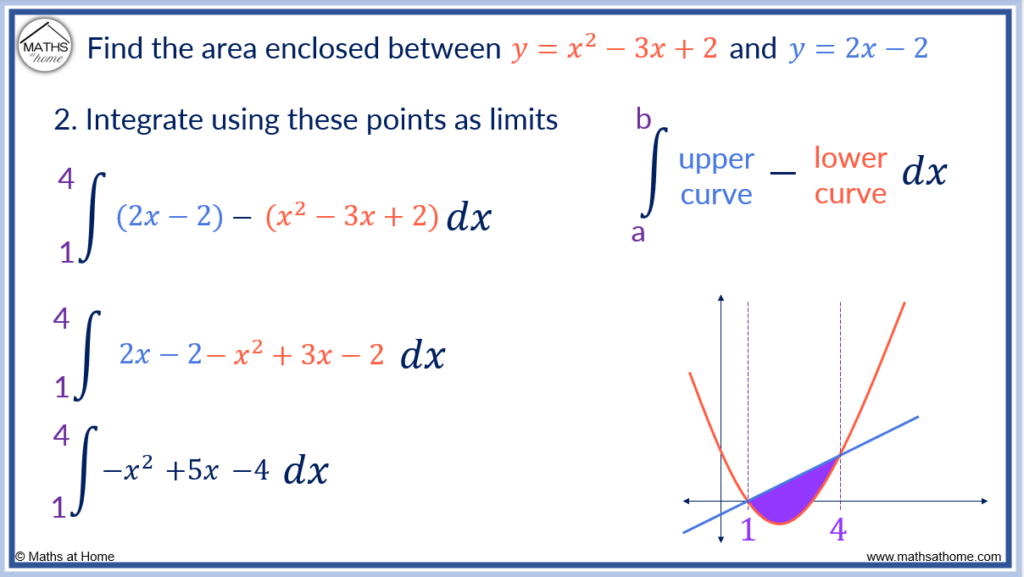
integrating to find the area between two curves with area below the x-axis

Integrating between this range:

the integral from 1 to 4 of negative x squared plus 5 x minus 4 d x becomes open bracket negative the fraction with numerator x cubed and denominator 3 plus 5 x squared over 2 minus 4 x close bracket sub sub 1 to the fourth power.

Evaluating the integral, 2 and two thirds plus 1 and five sixths equals 4.5 u n i t s squared.

The area between the two curves is 4.5 units2.

It does not matter that the area went below the x-axis. The area is still given by the integral of the upper curve minus the lower curve.

how to integrate with limits

Finding the Area Between Two Exponential Curves

In this example, the area between two exponential curves is found.

Find the area enclosed between the exponential curves y equals e raised to the 2 x power and y equals e to the x-th power between 𝑥=0 and 𝑥=2.

The equation of the upper curve is y equals e raised to the 2 x power and the equation of the lower curve is y equals e to the x-th power.

The limits of integration are given as 0 and 2. Therefore the area between the two curves is given by:

the integral from 0 to 2 of e raised to the 2 x power minus e to the x-th power d x which becomes open bracket the fraction with numerator e raised to the 2 x power and denominator 2 minus e to the x-th power close bracket sub sub 0 squared.

Evaluating this, the exact answer is the fraction with numerator e to the fourth power and denominator 2 minus e squared plus 1 over 2 u n i t s squared.

This is approximately 20.410 units2.

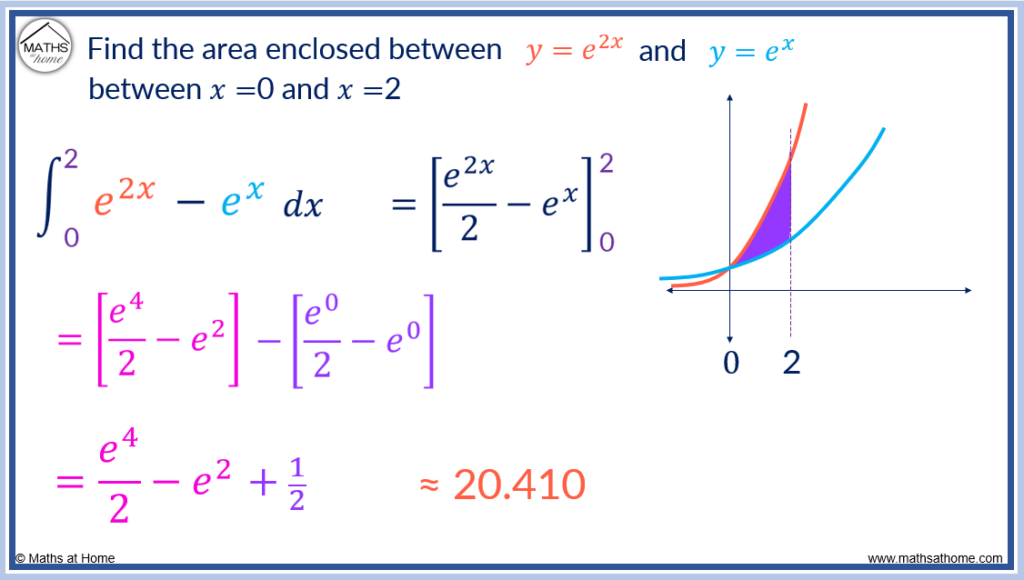
how to find the area between two exponential curves

Finding the Area Between Two Trigonometric Curves

For example, find the area bound between the curves sin(x) and cos(x) within the range 0 is less than or equal to x is less than or equal to 2 pi.

The first step is to find the points of intersection between the curves of sin(𝑥) and cos(𝑥).

Set the equations of the curves equal to each other: sine x equals cosine x.

Divide both sides of the equation by cos(𝑥) to get: tangent x equals 1.

Find the two angles within the range of 0 is less than or equal to x is less than or equal to 2 pi for which tan(𝑥)=1.

x equals pi over 4 or x equals 5 pi over 4.

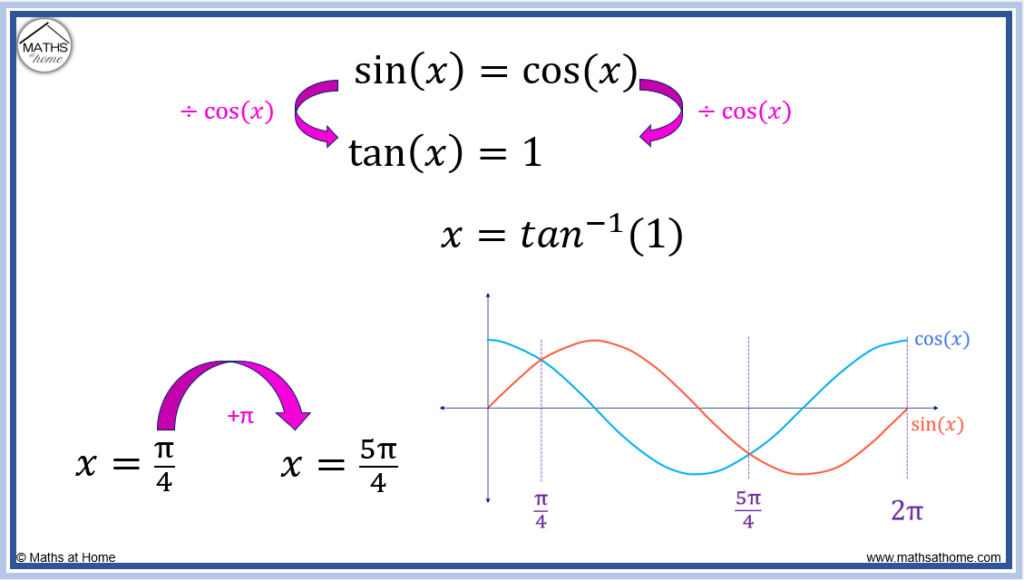
finding the points of intersection between sinx and cosx

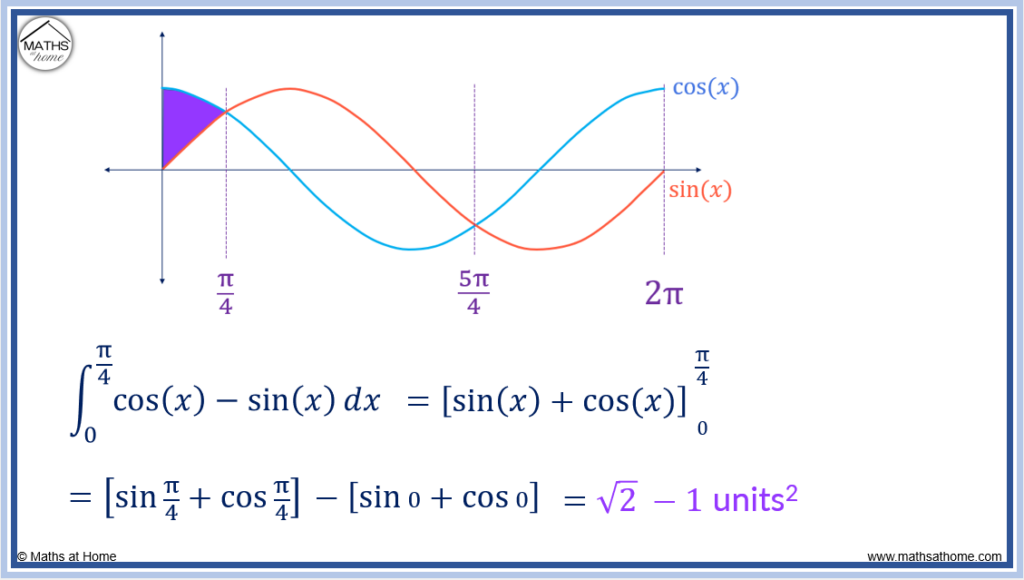
The next step is to find the area bound between sin(𝑥) and cos(𝑥) from 𝑥=0 and x equals pi over 4.

The limits of integration are therefore 0 and pi over 4.

In this region, the upper curve is y equals cosine x and the lower curve is y equals sine x.

The area of this region is therefore found as the integral from 0 to pi over 4 of cosine x minus sine x d x.

Integrating, the area is found as open bracket sine x plus cosine x close bracket sub sub 0 raised to the pi over 4 power.

Evaluating the limits the integral becomes open bracket the sine of open paren pi over 4 close paren plus the cosine of open paren pi over 4 close paren close bracket minus open bracket sine 0 plus cosine 0 close bracket.

the sine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2, the cosine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2, sine 0 equals 0 and cosine 0 equals 1.

Evaluating this, the area is the square root of 2 minus 1 u n i t s squared.

area between sin(x) and cos(x)

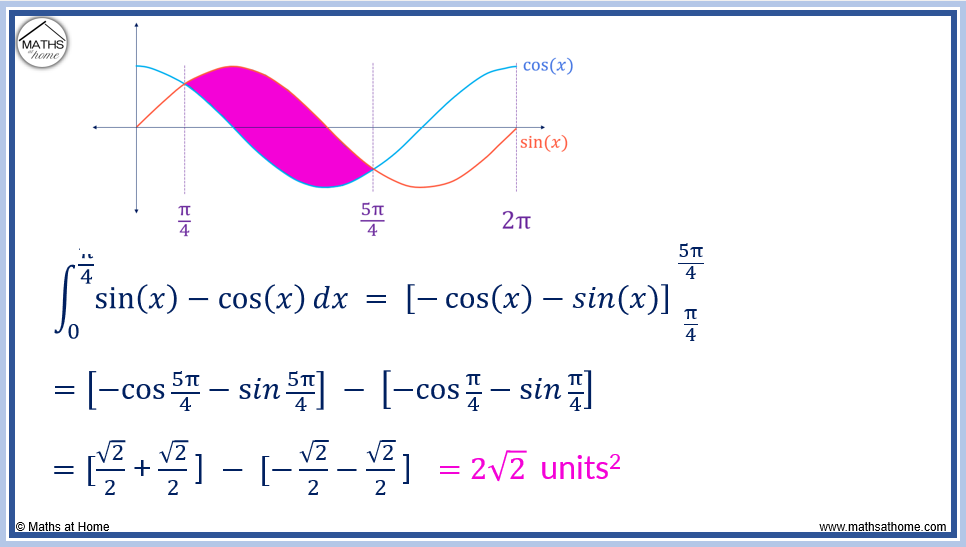
The next step is to find the area bound between sin(𝑥) and cos(𝑥) in the range pi over 4 is less than or equal to x is less than or equal to 5 pi over 4.

In this region, the upper curve is sin(𝑥) and the lower curve is cos(𝑥).

The area is found with the integral the integral from pi over 4 to 5 pi over 4 of sine x minus cosine x d x.

Completing the integration we obtain: open bracket negative cosine x minus sine x close bracket sub pi over 4 raised to the 5 pi over 4 power.

Evaluating the limits: open bracket negative the cosine of open paren 5 pi over 4 close paren minus the sine of open paren 5 pi over 4 close paren close bracket minus open bracket negative the cosine of open paren pi over 4 close paren minus the sine of open paren pi over 4 close paren close bracket.

the cosine of open paren 5 pi over 4 close paren equals negative the fraction with numerator the square root of 2 and denominator 2, the sine of open paren 5 pi over 4 close paren equals negative the fraction with numerator the square root of 2 and denominator 2, the cosine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2 and the sine of open paren pi over 4 close paren equals the fraction with numerator the square root of 2 and denominator 2.

Therefore the integral becomes open bracket the fraction with numerator the square root of 2 and denominator 2 plus the fraction with numerator the square root of 2 and denominator 2 close bracket negative open bracket negative the fraction with numerator the square root of 2 and denominator 2 minus the fraction with numerator the square root of 2 and denominator 2 close bracket which equals 2 the square root of 2 u n i t s squared.

how to find the area between sinx and cosx using trigonometry between pi/4 and 5pi/4

The next step is to find the area between sin(𝑥) and cos(𝑥) in the range 0 is less than or equal to x is less than or equal to 2 pi.

The upper curve is cos(𝑥) and the lower curve is sin(𝑥).

The area between the curves is found with the integral: integral from 5 pi over 4 to 2 pi cosine x minus sine x d x.

Completing the integration: open bracket sine x plus cosine x close bracket sub 5 pi over 4 raised to the 2 pi power.

Evaluating the limits, this becomes: open bracket sine 2 pi plus cosine 2 pi close bracket minus open bracket the sine of open paren 5 pi over 4 close paren plus the cosine of open paren 5 pi over 4 close paren close bracket.

sine 2 pi equals 0, cosine 2 pi equals 1, the sine of open paren 5 pi over 4 close paren equals negative the fraction with numerator the square root of 2 and denominator 2 and the cosine of open paren 5 pi over 4 close paren equals negative the fraction with numerator the square root of 2 and denominator 2.

The integral becomes: open bracket 0 plus 1 close bracket minus open bracket negative the fraction with numerator the square root of 2 and denominator 2 minus the fraction with numerator the square root of 2 and denominator 2 close bracket which equals 1 plus the square root of 2 u n i t s squared.

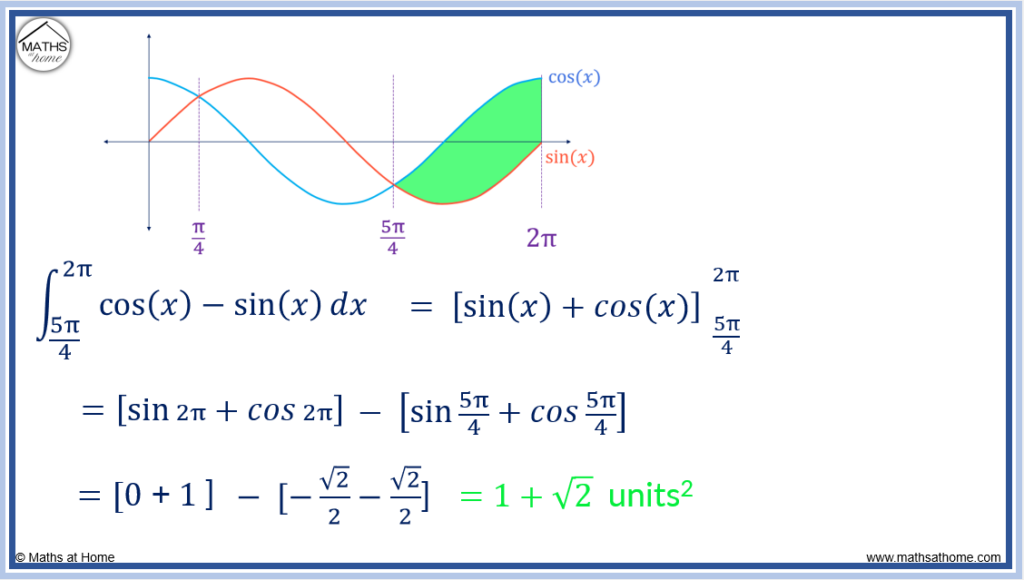
area between cosx and sinx between 5pi/4 and 2pi

The total area between the curves is found by adding the areas of the three individual regions.

1 lines Line 1: open paren the square root of 2 minus 1 close paren plus open paren 2 the square root of 2 close paren plus open paren 1 plus the square root of 2 close paren equals 4 the square root of 2

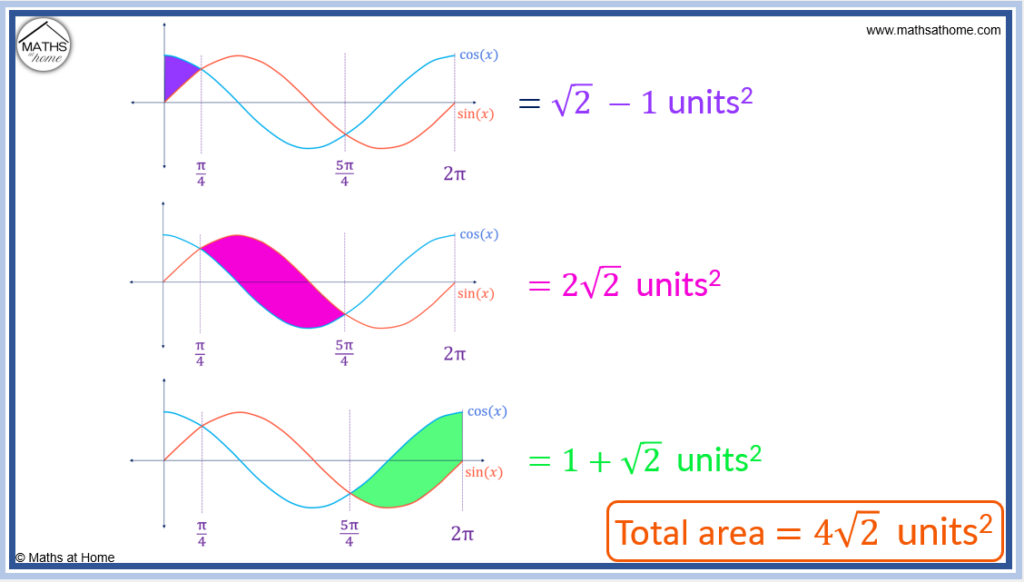
total area between sinx and cosx from 0 to 2pi

The total area between sin(𝑥) and cos(𝑥) from 0 to 2π is 1 lines Line 1: 4 the square root of 2 u n i t s squared.

Area Between Two Curves with Respect to Y-Axis

To find the area between two curves with respect to the y-axis, integrate the equation of the rightmost curve minus the leftmost curve with respect to y. The limits of integration are the lower and upper points on the y-axis either side of the area required.

For example, find the area bound between the curves 𝑥 = 3y – y2 and x = 0.5y2.

To find the area between two curves with respect to the y-axis, integrate the rightmost equation minus the leftmost equation.

For the region shown, between y=0 and y=2, the rightmost equation is x = 3y – y2 and the left most equation is x = 0.5y2.

Subtracting the 0.5y2 from 3y – y2, the result is 3y – 1.5y2.

The area is found with the integral: the integral from 0 to 2 of 3 y minus 1.5 y squared d y.

Completing the integration: open bracket 1.5 y squared minus 0.5 y cubed close bracket sub 0 squared.

Evaluating the limits: open bracket 1.5 times 2 squared minus 0.5 times 2 cubed close bracket minus open bracket 1.5 times 0 squared minus 0.5 times 0 cubed close bracket.

This calculation becomes : open bracket 6 minus 4 close bracket minus open bracket 0 minus 0 close bracket which equals 2 u n i t s squared.

area between two curves with respect to the y-axis