How to Find the Equation of a Line From Two Points

Video Lesson: How to Find the Equation of a Line when Given Two Points

The equation of a straight line can be calculated if two points it passes through are known. The equation can be written in the slope-intercept form, y = m𝑥 + c (sometimes written as y = m𝑥 + b) or the point-slope form, y – y1 = m(𝑥 – 𝑥1).

Both of these forms can be rearranged to write the equation in the general form, a𝑥 + by = c.

point slope form and slope intercept form equations

The point-slope form of the equation of a line is easier to calculate as only the value of the slope (m) is required. This is either given to us or we can calculate it from two points.

The gradient can be easily seen from an equation in point-slope form as it is the number in front of the brackets.

For example, the gradient of y minus 3 equals 2 times open paren x minus 1 close paren is 3.

The slope-intercept form of the line requires both the value of the slope (m) and the y-intercept (c). However it is beneficial in that both of these values can be easily read from the equation. The slope is the coefficient of 𝑥 and the y-intercept is the constant term added to the 𝑥 term.

For example, the gradient of y equals 5 x plus 3 is 5 and the y-intercept is 3.

The slope-intercept form of the line is generally shorter and simpler to write. Since it conveys more information, it is the most common way to write the equation of a straight line.

How to Find the Equation of a Line from Two Points

To find the equation of a line given two points:
  1. Label one point as (𝑥1, y1) and the other point as (𝑥2, y2).
  2. Calculate the slope using m = (y2 – y1) ÷ (𝑥2 – 𝑥1).
  3. Substitute m and either (𝑥1, y1) or (𝑥2, y2) into y = m𝑥 + c.
  4. Solve the resulting equation for c.
  5. Write the equation of the line as y = m𝑥 + c using the calculated values of m and c.

For example, find the slope-intercept form of the equation of the line passing through the two points (5, 2) and (9, 6).

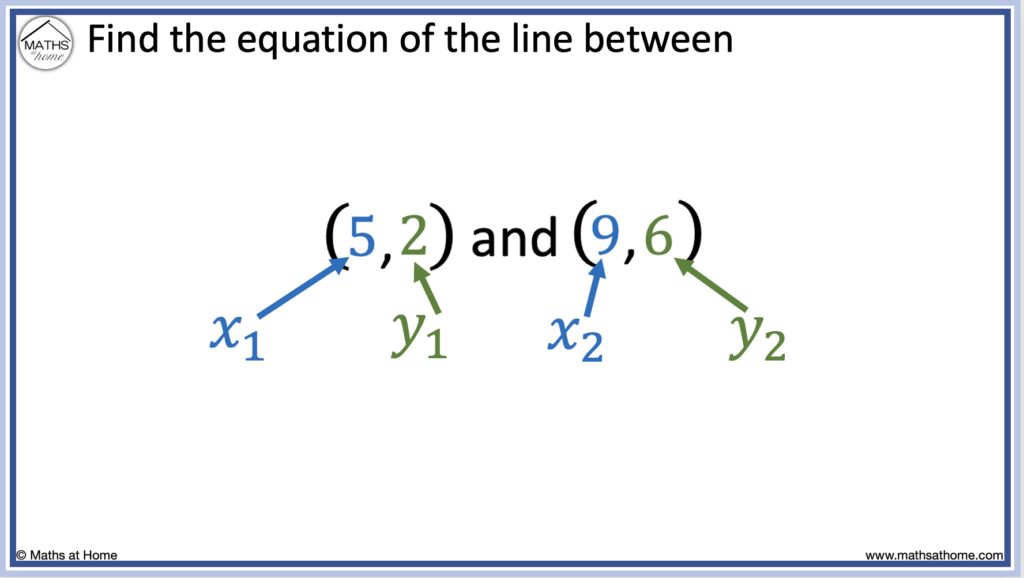
example of finding the equation of a line between two points

Step 1. Label one point as (𝑥1, y1) and the other point as (𝑥2, y2)

The values must be labelled in the order: (𝑥1, y1) and (𝑥2, y2).

That is the 𝑥1 and y1 values are from the first point and the 𝑥2 and y2 values are from the second point.

Considering the points: (5, 2) and (9, 6), we obtain the following values:

  • 𝑥1 = 5
  • y1 = 2
  • 𝑥2 = 9
  • y2 = 6

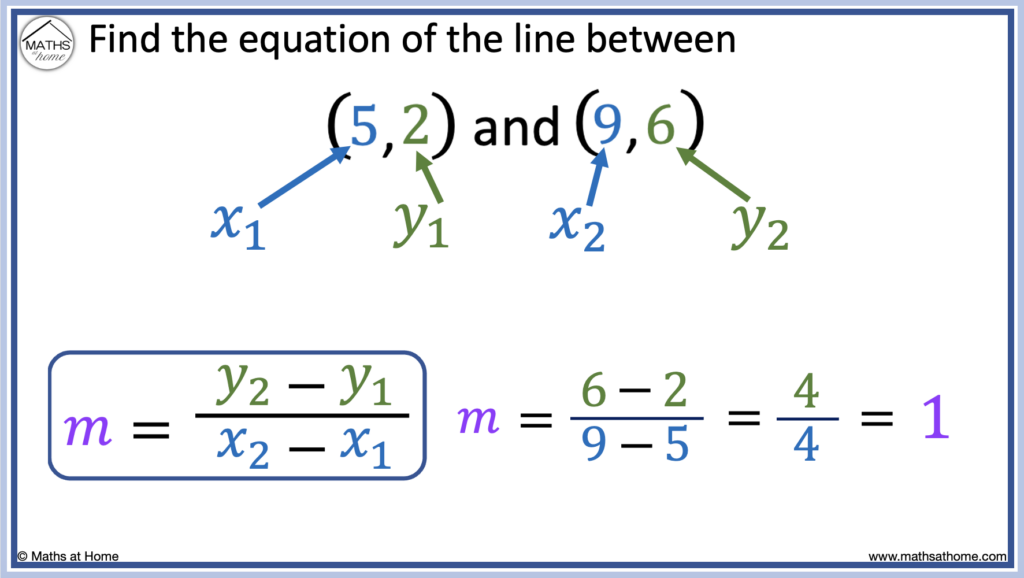
Step 2. Calculate the slope using m = (y2 – y1) ÷ (𝑥2 – 𝑥1)

Substituting the values listed above, we obtain:

m equals open paren 6 minus 2 close paren divided by open paren 9 minus 5 close paren

This becomes m equals 4 divided by 4 equals 1

and so, m equals 1.

calculating the gradient between two points

Step 3. Substitute m and either (𝑥1, y1) or (𝑥2, y2) into y = m𝑥 + c

Either point can be chosen, so we will use the first point of (5, 2).

Therefore we will substitute:

  • 𝑥 = 5
  • y = 2
  • m = 1

into the equation of a straight line: y equals m x plus c

Therefore, y equals m x plus c becomes 2 equals 1 times 5 plus c

how to find the equation of a line between two points

Step 4. Solve the resulting equation for c

2 equals 1 times 5 plus c becomes 2 equals 5 plus c and so, c equals negative 3.

Step 5. Write the equation of the line as y = m𝑥 + c using the calculated values of m and c

Now we have m = 1 and c = -3.

y equals m x plus c can be written as y equals x minus 3.

The equation of the line in slope-intercept form is y equals x minus 3.

We can write the steps to find the equation of a straight line in simple terms.

The steps for the equation of a straight line given two points are:
  1. Calculate the slope, m.
  2. Substitute m into y = m𝑥 + c.
  3. Substitute either coordinate to work out c.
steps to find the equation of a line from two points

Examples of Calculating the Slope-Intercept Equation of a Line when Given Two Points

Find the equation of the line between (1, 5) and (2, 8).

Here, 𝑥1 = 1, y1 = 5 and 𝑥2 = 2, y2 = 8.

Step 1. Calculate the slope, m

The gradient (or slope) of the line is found using the equation: m equals the fraction with numerator open paren y sub 2 minus y sub 1 close paren and denominator open paren x sub 2 minus x sub 1 close paren

Therefore m equals the fraction with numerator open paren 8 minus 5 close paren and denominator open paren 2 minus 1 close paren equals 3.

Step 2. Substitute m into y = m𝑥 + c

Now that we know that m = 3,

y equals m x plus c can be written as y equals 3 x plus c.

Step 3. Substitute either coordinate to work out c

We can choose either (1, 5) or (2, 8).

In this example, we will choose (2, 8).

Therefore we substitute 𝑥 = 2 and y = 8 into y equals 3 x plus c.

Therefore, we obtain 1 lines Line 1: 8 equals 3 times 2 plus c.

1 lines Line 1: 8 equals 6 plus c and so, c = 2.

How to find the slope intercept form from two points

Having now calculated both m and c, we can write the equation of the straight line.

y equals m x plus c becomes y equals 3 x plus 2.

Formula for the Slope-Intercept Equation of a Line From Two Points

Given any two points, (𝑥1, y1) and (𝑥2, y2), the formula for the slope-intercept equation of a straight line is y = m𝑥 + c, where m = (y2 – y1) / (𝑥2 – 𝑥1) and c = y1 – m𝑥1.

y equals m x plus c

Slope-Intercept Equation of a Straight Line

Where: m equals the fraction with numerator open paren y sub 2 minus y sub 1 close paren and denominator open paren x sub 2 minus x sub 1 close paren and c equals y 1 minus m x sub 1.

formula for the equation of a line from two points
To use the formula for the equation of a line given two points:
  1. Calculate m = (y2 – y1) ÷ (𝑥2 – 𝑥1)/.
  2. Calculate c = y1 – m𝑥1.
  3. Substitute these values into y = m𝑥 + c

Examples of using the Formula for the Equation of a Line Given Two Points

Find the equation of the line passing through (3, 4) and (5, 8).

Step 1. Label the coordinates

Using the order (𝑥1, y1) and (𝑥2, y2), we have the following:

𝑥1 = 3 y1 = 4 𝑥2 = 5 y2 = 8

Step 2. Calculate the slope (m)

m equals the fraction with numerator open paren y sub 2 minus y sub 1 close paren and denominator open paren x sub 2 minus x sub 1 close paren and so, m equals the fraction with numerator open paren 8 minus 4 close paren and denominator open paren 5 minus 3 close paren equals four halves and therefore m equals 2.

Step 3. Calculate the y-intercept (c)

c equals y sub 1 minus m x sub 1 and so, c equals 4 minus 2 times 3 and therefore c equals negative 2.

Step 4. Form the equation

y equals m x plus c becomes y equals 2 x minus 2.

Formula for the equation of a line given two points example

Formula for the Point-Slope Equation of a Line Given Two Points

The formula for the point-slope equation of a straight line when given two points, (𝑥1, y1) and (𝑥2, y2), can be written as y – y1 = m(𝑥 – 𝑥1), where m = (y2 – y1) / (𝑥2 – 𝑥1).

y minus y sub 1 equals m times open paren x minus x sub 1 close paren

Point-Slope Equation of a line when Given Two Points

The point-slope form of the equation of a line is always written as y – y1 = m(𝑥 – 𝑥1).

The point-slope equation is easy to obtain as only the gradient and one point is required. The disadvantage to the point-slope form is that the y-intercept is not obvious until the equation is rearranged.

equation of a line given two points

For example, find the point-slope equation of the line passing through the points (7, 2) and (3, 0).

Therefore: 𝑥1 = 7 —- y1 = 2 —- 𝑥2 = 3 —- y2 = 0.

Firstly, the slope (m) is calculated: m equals the fraction with numerator open paren 0 minus 2 close paren and denominator open paren 3 minus 7 close paren equals one half

Then the values of m, y1 and 𝑥1 are substituted into y minus y sub 1 equals m times open paren x minus x sub 1 close paren.

We obtain the point-slope form of the equation as y minus 2 equals one half times open paren x minus 7 close paren.

The formula for the equation of a straight line in slope-intercept form can be written as y = [ (y2 – y1) / (𝑥2 – 𝑥1) ] (𝑥 –𝑥1) + y1.

Equation of a Line From Two Points: Calculator

This calculator calculates the equation of a line from two given points. Simply enter the two coordinates and the calculator will calculate the gradient (m) and y-intercept (c) for any straight line written in slope-intercept form (y = m𝑥 + c).

To use this calculator, you must have two different coordinates.

Steps for using the calculator:

  • Choose one point to be the first point (𝑥1, y1) and the other point to be the second point (𝑥2, y2). It does not matter which one is which.
  • Enter both numbers from the first point (𝑥1, y1) in the first row of the calculator.
  • Enter both numbers from the second point (𝑥2, y2) in the second row of the calculator.
  • The calculator will then tell you the values of m and c for the line.
  • Write y = m𝑥 + c but replace m and c with the values given on the calculator to obtain your equation. Note, if c is negative, we write a subtraction instead of an addition as in the example below.
equation of a line from two points calculator
Each point is made up of an 𝑥 coordinate and a y coordinate.

The numbers must be entered in the order: 𝑥1, y1, 𝑥2, y2.

slope intercept equation of a line from two points calculator example
In the example (2, 1) and (4, 7), we have:

𝑥1 = 2 —- y1 = 1 —- 𝑥2 = 4 —- y2 = 7

In the example above, the calculator calculated m = 3 and c = -5.

Therefore we write y = 3𝑥 – 5.

We don’t write y = 3𝑥 + – 5.

We keep ‘y’ and ‘𝑥’ as ‘y’ and ‘𝑥’. We only substitute the values of m and c.

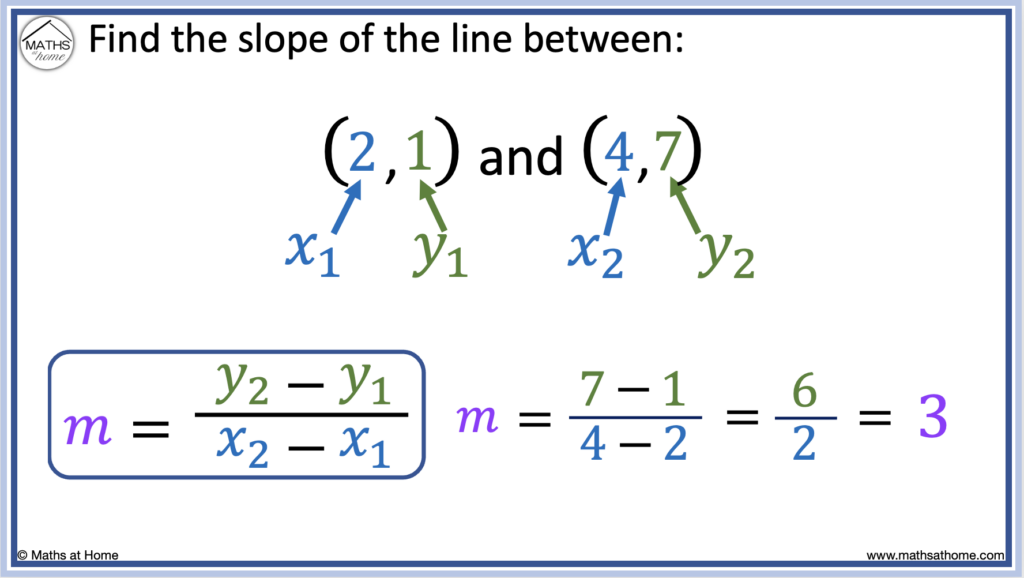
How to Find the Slope from Two Points

When given two points (𝑥1, y1) and (𝑥2, y2), the slope is calculated using the formula: slope = (y2 – y1) ÷ (𝑥2 – 𝑥1). For example, the slope between (2, 1) and (4, 7) is calculated as slope = (7 – 1) ÷ (4 – 2). This is evaluated as slope = 6 ÷ 2 = 3.

how to calculate the slope between two points

How to Find the y-intercept from Two Points

The formula for the y-intercept of a line passing through two points (𝑥1, y1) and (𝑥2, y2) is c = y1 – m𝑥1, where m = (y2 – y1) ÷ (𝑥2 – 𝑥1).

c equals y sub 1 minus m x sub 1 where m equals the fraction with numerator open paren y sub 2 minus y sub 1 close paren and denominator open paren x sub 2 minus x sub 1 close paren

Formula for the y-intercept from two points

For example, calculate the y-intercept of the line passing through the two points (2, 9) and (3, 13).

Step 1. Label the coordinates

Using the order (𝑥1, y1) and (𝑥2, y2):

  • 𝑥1 = 2
  • y1 = 9
  • 𝑥2 = 3
  • y2 = 13

Step 2. Calculate m

m = (y2 – y1) ÷ (𝑥2 – 𝑥1)

Using the values of

  • 𝑥1 = 2
  • y1 = 9
  • 𝑥2 = 3
  • y2 = 13

m equals the fraction with numerator open paren 13 minus 9 close paren and denominator open paren 3 minus 2 close paren

We obtain, m equals four oneths and so, m equals 4.

Step 3. Calculate the y-intercept

The formula for the y-intercept given two points is c equals y sub 1 minus m x sub 1.

Using the values of m = 4, 𝑥1 = 2 and y1 = 9:

c equals 9 minus 4 times 2 equals 1

Therefore, c = 1.

how to calculate the y-intercept from two points