How to Place Fractions on a Number Line
To place fractions on a number line:
- Subtract one from the denominator of the fraction.
- Draw this many evenly-spaced lines between each whole number.
- Locate the whole number part of the fraction on the number line.
- Count on from here by the number of lines equal to the numerator of the fraction.
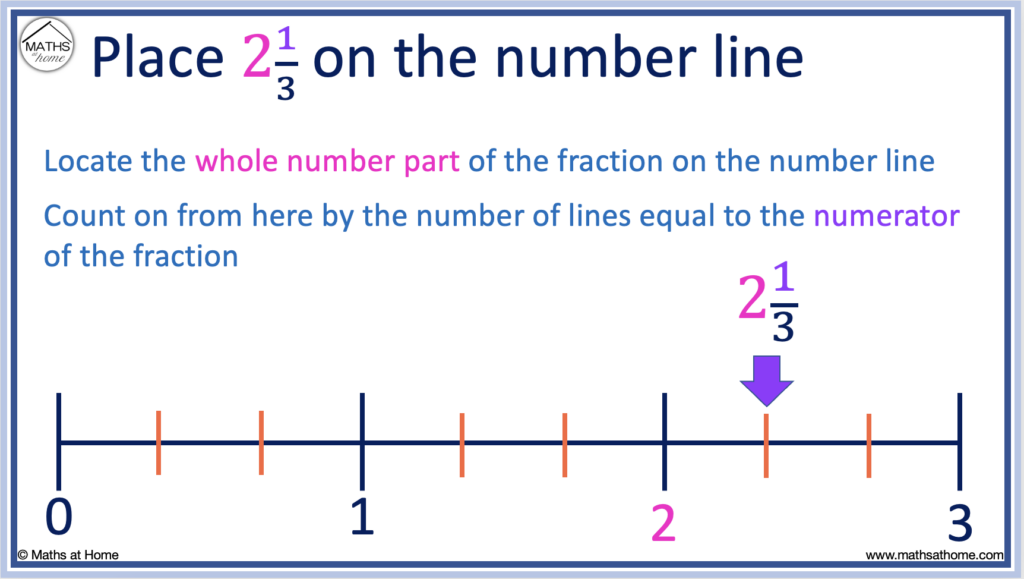
For example, place the fraction 2 1/3 on a number line.
2 1/3 is a mixed number.
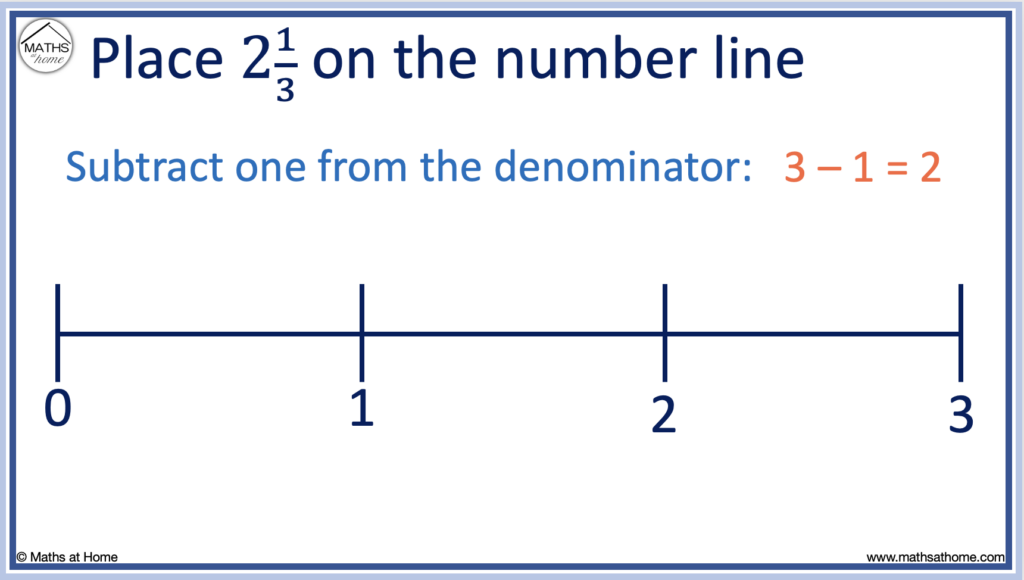
Step 1. Subtract one from the denominator of the fraction
The denominator is the number on the bottom of the fraction.
We have a 3 on the denominator of the fraction of 2 1/3.
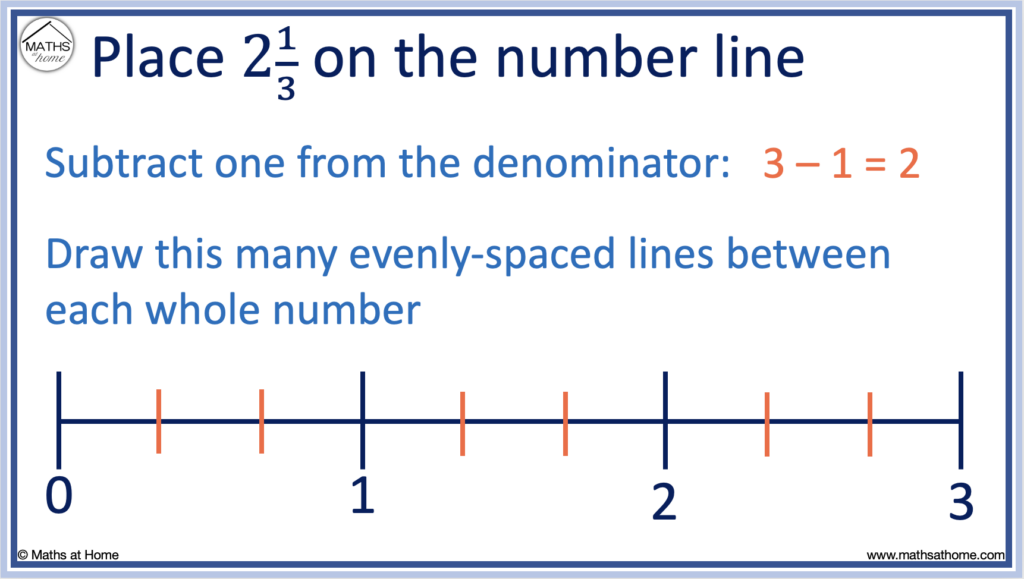
3 – 1 = 2 and so, we draw 2 lines between each whole number on the number line to divide it into thirds.
We draw the lines equally spaced so that each whole number is divided into equal parts.
Step 2. Draw this many evenly-spaced lines between each whole number
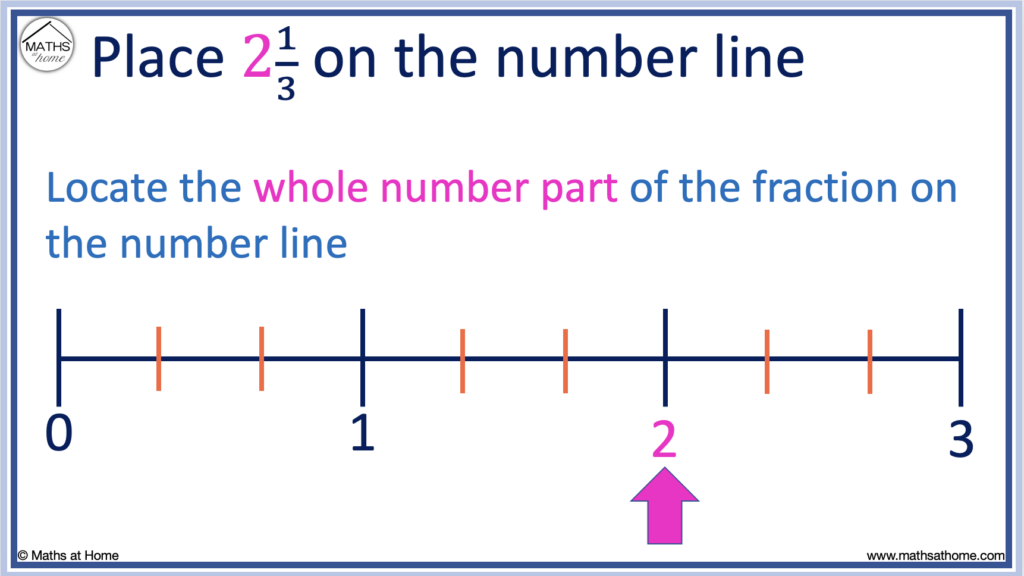
Step 3. Locate the whole number part of the fraction on the number line
In the fraction 2 1/3, the whole number is 2.
Therefore we move to the position of 2.
Step 4. Count on from here by the number of lines equal to the numerator of the fraction
The numerator is the number on top of a fraction.
In the fraction 2 1/3, the numerator of the fraction is 1.
So we count on from the number 2 by 1 more line.
This is the position of the fraction 2 1/3.
Here is another example of plotting a mixed fraction on a number line.
Plot the fraction 1 3/4 on the number line.
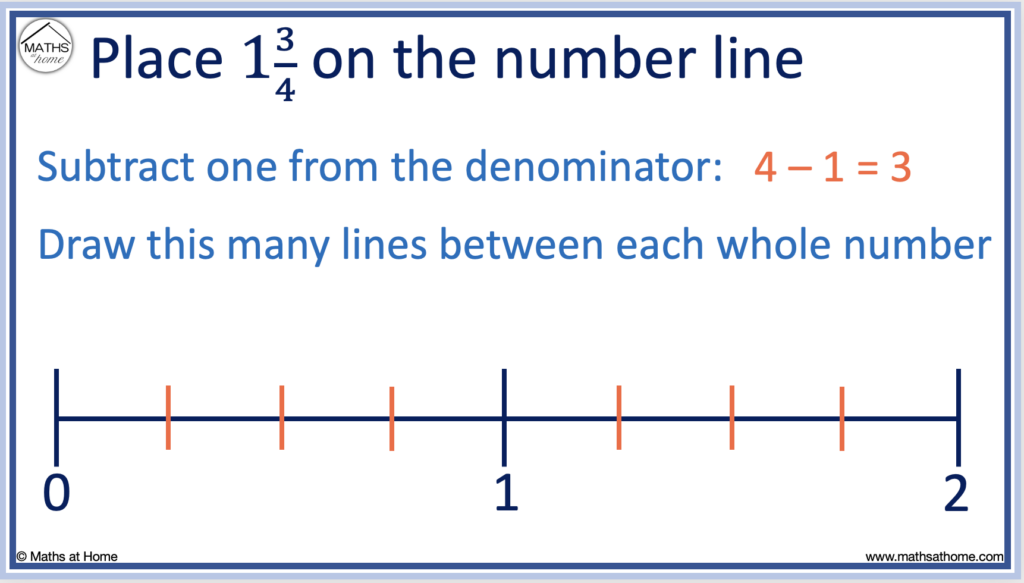
Step 1. Subtract one from the denominator of the fraction
Step 2. Draw this many evenly-spaced lines between each whole number
On the fraction 1 3/4, the denominator is 4.
4 – 1 = 3 and so, we draw 3 lines between each whole number to divide them into quarters.
Step 3. Locate the whole number part of the fraction on the number line
Step 4. Count on from here by the number of lines equal to the numerator of the fraction
The fraction of 1 3/4 has a whole number

Examples of Fractions on a Number Line
In this section we display different types of fractions on a number line.
Different charts are used to display the different types of fraction.
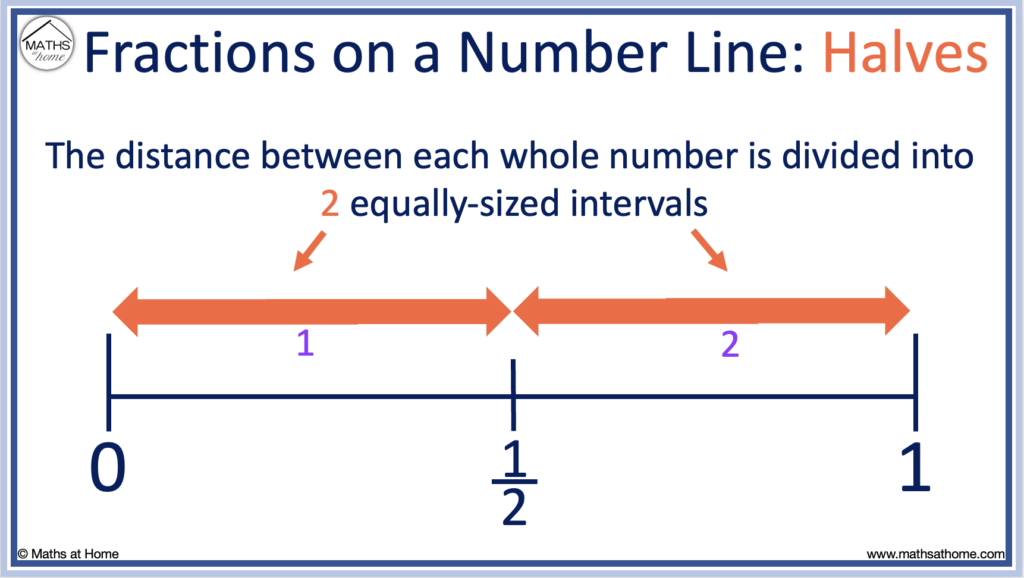
The number line below shows halves from 0 to 1.
Divide the number line so that there are 2 parts between each whole number.
The fraction 1/2 is found at the halfway point between 0 and 1.
Here is a number line containing halves for numbers beyond 1.
A line separates each whole number to divide them into halves.

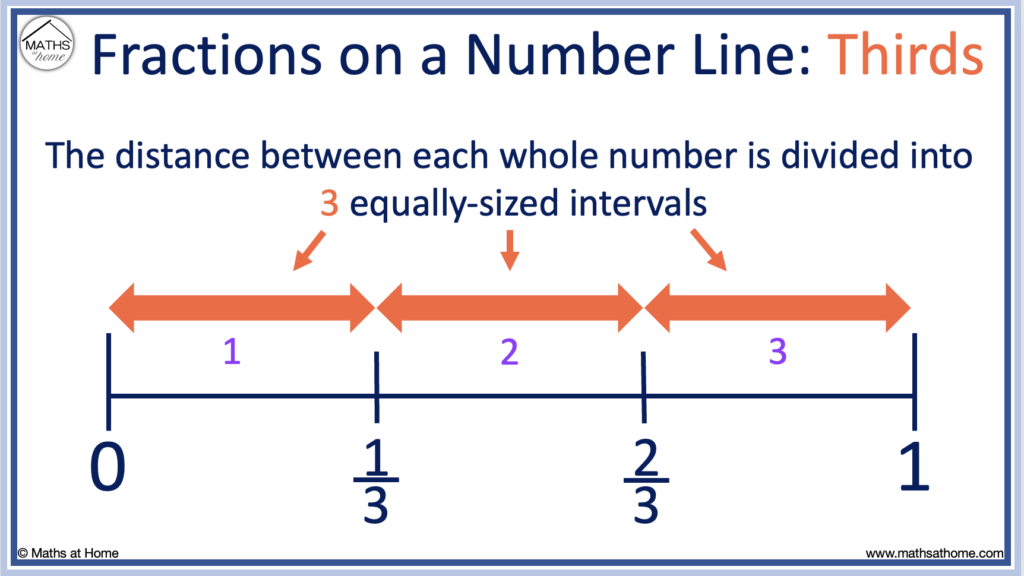
To place one third on a number line:
Draw two equally-spaced lines between 0 and 1 to divide the line into thirds.
One third is located at the first of these lines.
1/3 is found at the first line drawn between 0 and 1.
2/3 is found at the first line drawn between 0 and 1.
The number line below shows thirds beyond 1 whole.
Divide each whole number into thirds by drawing two equally-spaced lines between them.
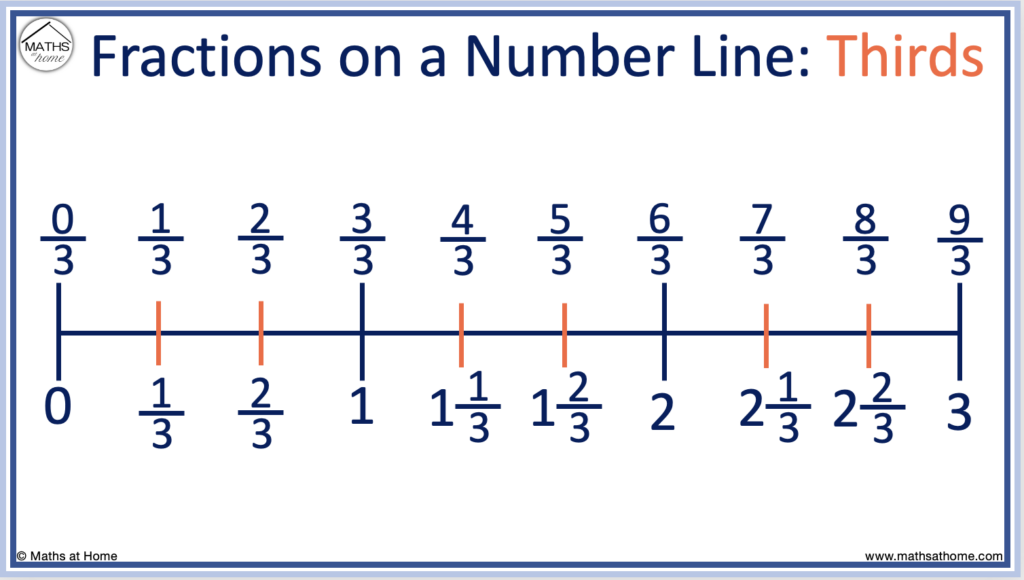
The number line below shows thirds from zero to five.
Improper fractions are shown on the top of the number line.
Improper fractions are fractions in which the numerator on top of the fraction is a larger number than the denominator on the bottom of the fraction.
When counting up in thirds, the denominator remains as a ‘3’ but the numerator increases by 1 each time.

3/3 is equal to one whole.
6/3 is equal to 2.
9/3 is equal to 3.
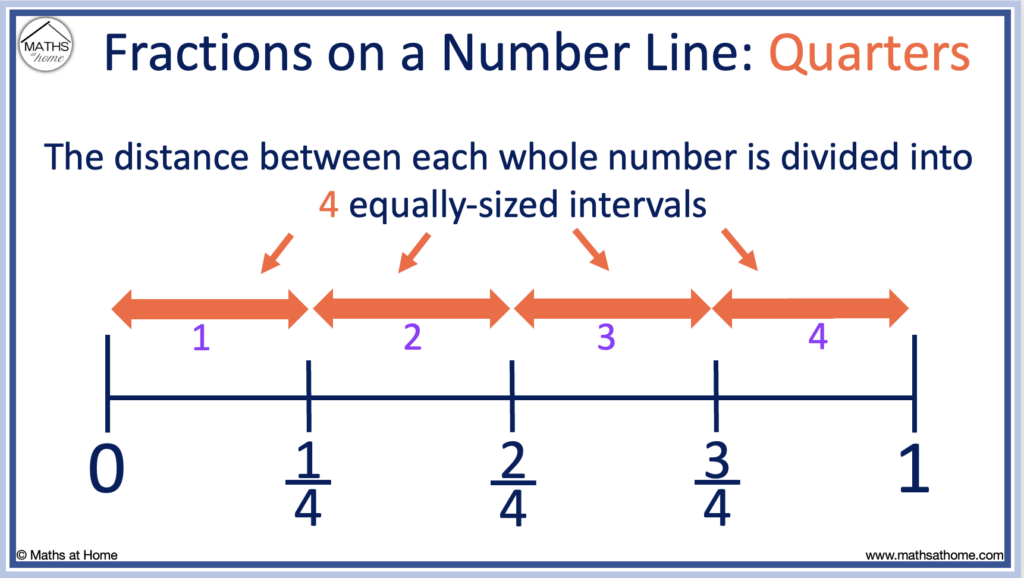
To place one quarter on a number line
Divide the distance from 0 to 1 into quarters by drawing three equally-spaced lines.
1/4 is positioned on the first line between 0 and 1.
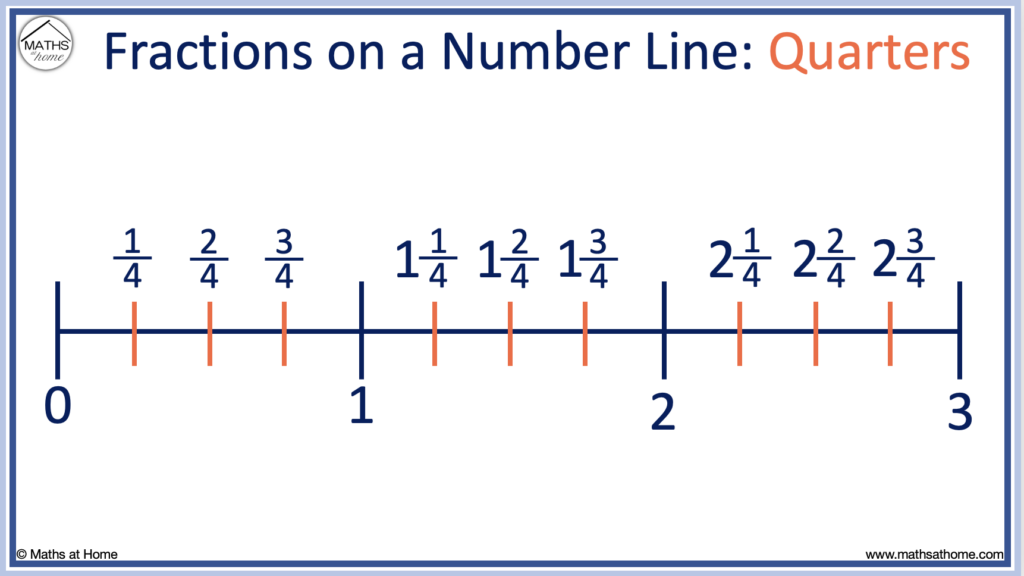
Quarters greater than 1 are shown on the following number line.
To locate quarters on a number line, divide each whole number into four parts using three equally-spaced lines.
To place one fifth on a number line
Divide the distance from 0 to 1 into fifths by drawing four equally-spaced lines.
1/5 is positioned on the first of these lines between 0 and 1.
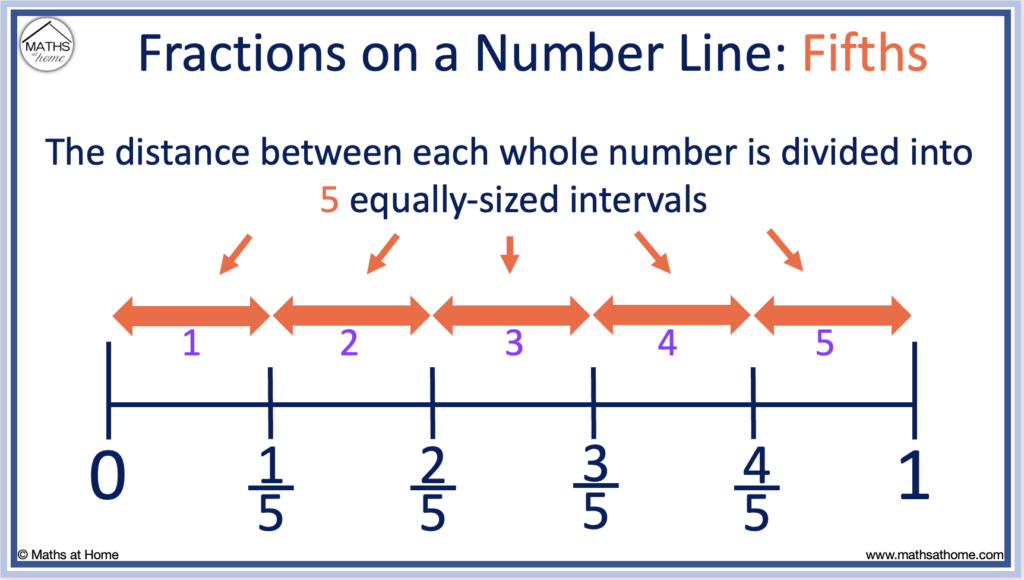
The number line below shows fifths on greater than 1 whole on a number line.

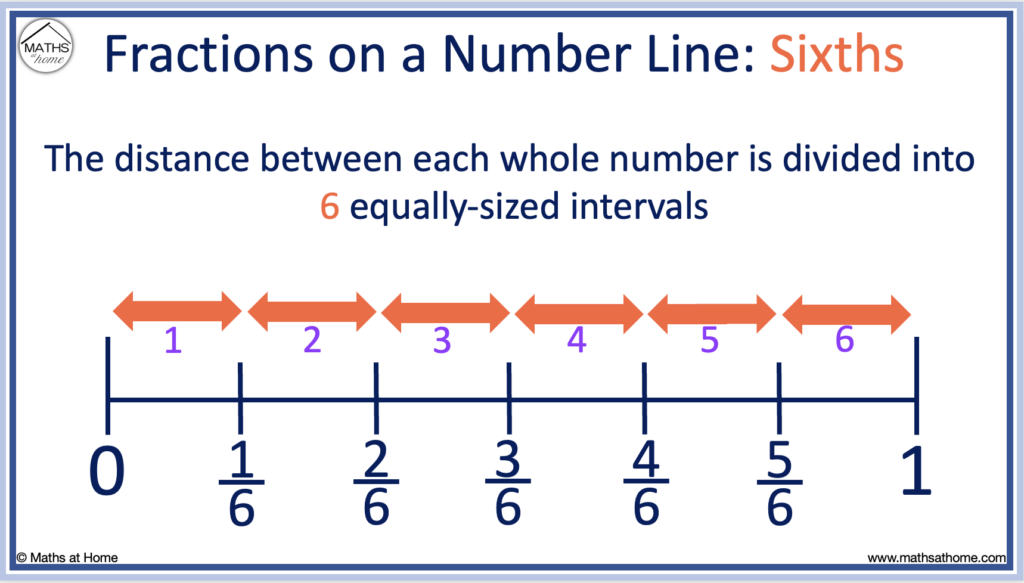
To place sixths on a number line
Divide each whole number into sixths by drawing five equally-spaced lines between them.
1/6 is positioned on the first of these lines between 0 and 1.
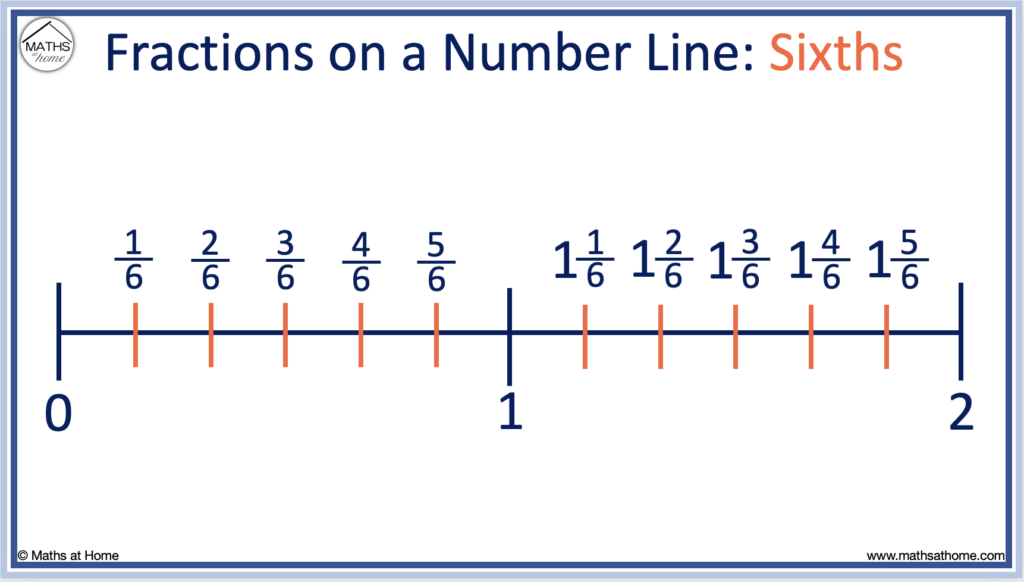
The number line below shows sixths beyond one whole.
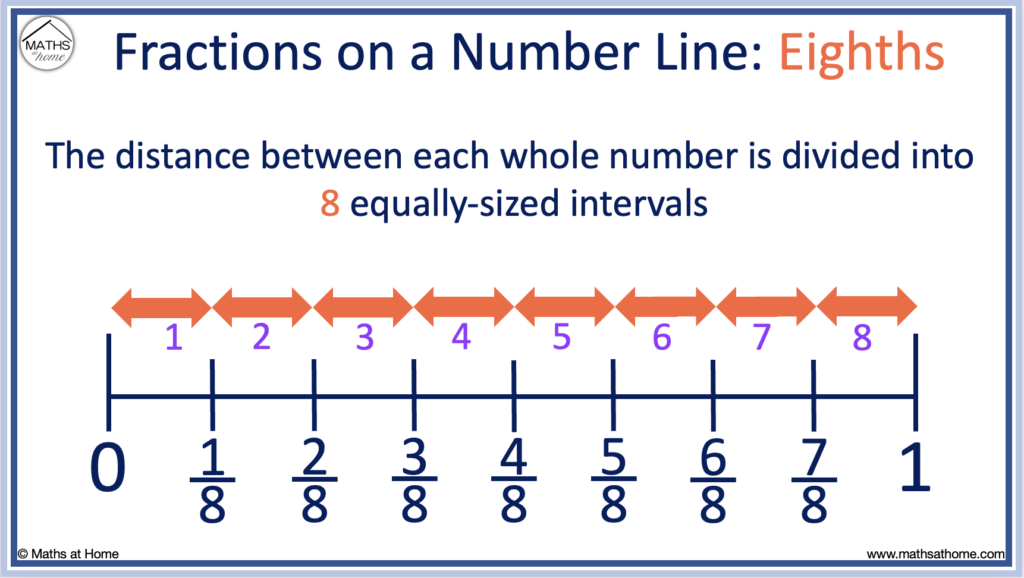
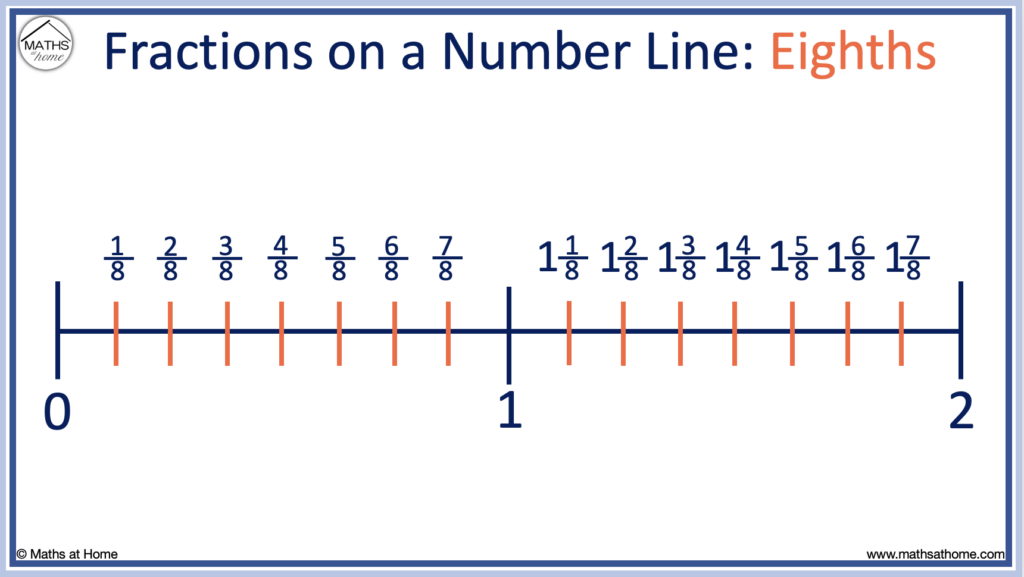
To place eighths on a number line
Divide each whole number into eighths by drawing seven equally-spaced lines between them.
1/8 is positioned on the first of these lines between 0 and 1.
The number line below shows eighths greater than one whole.
To place tenths on a number line
Divide each whole number into tenths by drawing nine equally-spaced lines between them.
1/10 is positioned on the first of these lines between 0 and 1.

The number line below shows tenths greater than one whole.

Negative Fractions on a Number Line
Negative fractions are shown on a number line to left of zero. The further left, the larger the size of the negative fraction. Divide each negative whole number into equally-sized parts to split them into fractions.
For example, the number line below shows negative fractions of one half.
Each whole number is divided into two halves by drawing a line between them.
–1/2 is the first line to the left of zero between zero and negative one.

- Subtract one from the denominator of the fraction.
- Draw this many evenly-spaced lines between each whole number to the left of zero.
- Locate the whole number part of the fraction on the number line.
- Count on further left from here by the number of lines equal to the numerator of the fraction.
For example, place -1 2/3 on the number line.
Subtract one from the denominator of the fraction
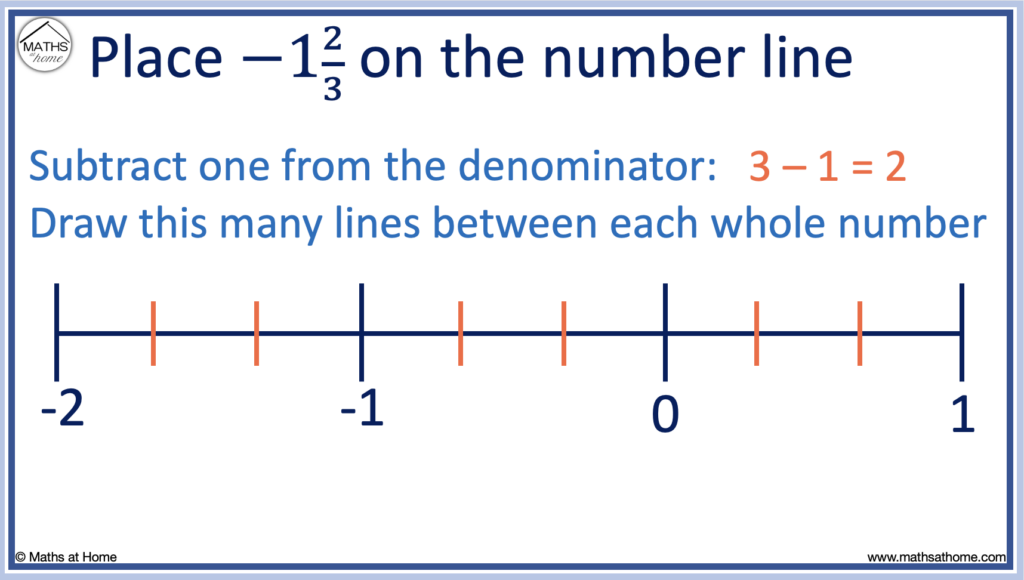
The denominator of the fraction is the number on the bottom of the fraction. In this example, the denominator is 3.
3 – 1 = 2.
Draw this many evenly-spaced lines between each whole number to the left of zero
Each whole number is split into thirds by drawing two evenly-spaced lines between them.
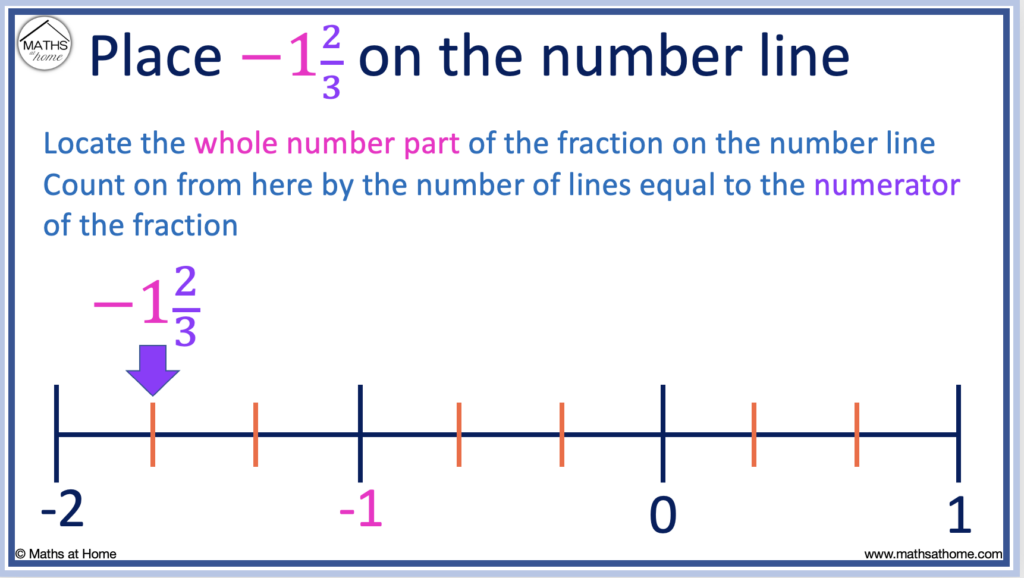
Locate the whole number part of the fraction on the number line
The whole number part of the fraction of -1 2/3 is -1.
-1 is the first whole number to the left of zero.
Count on further left from here by the number of lines equal to the numerator of the fraction
The numerator of the fraction is the number on top of the fraction. In this example, the numerator is 2.
We count left 2 more places.
Therefore -1 2/3 is located by counting on two more thirds to the left of -1. It is shown on the number line below.
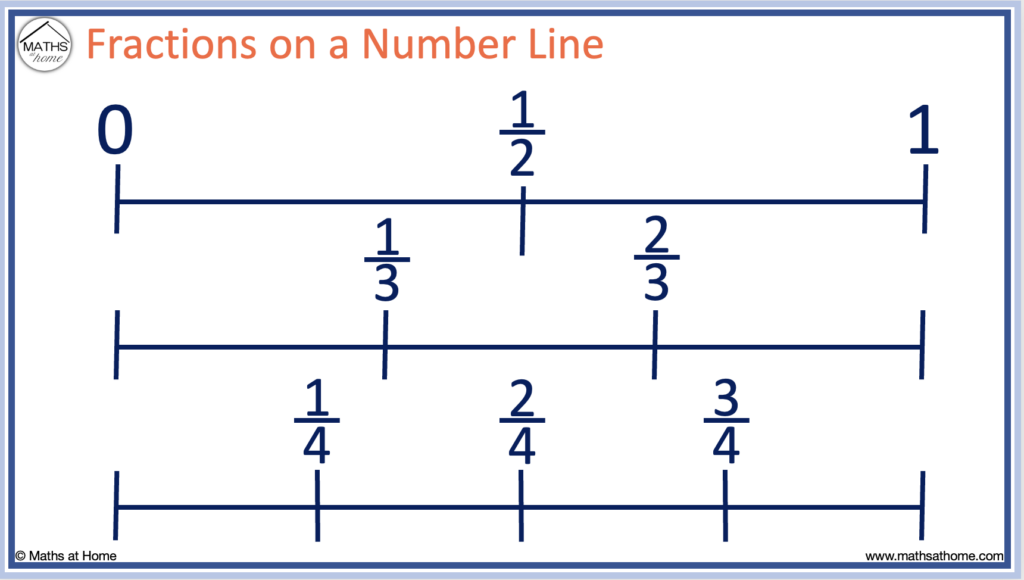
Benchmark Fractions on a Number Line
Benchmark fractions are well known reference amounts that other fractions and quantities can be easily compared to. Some examples include one half, one third and one quarter. Their sizes are commonly understood and they can be used in easily in speech for describing amounts.
For example, to explain how large 4/7 is, we can say that it is slightly larger than 1/2 but less than 2/3.
Here are some benchmark fractions shown on a number line. This chart can be used to better visualise benchmark fractions
Fractions and Decimals on a Number Line
Common fractions written as decimals include:- 1/8 = 0.125
- 1/5 = 0.2
- 1/4 = 0.25
- 1/3 = 0.333…
- 1/2 = 0.5
- 3/4 = 0.75

Unit Fractions on a Number Line
Unit fractions are fractions that have a numerator equal to 1. The denominator tells us how many equally-sized parts one whole is divided into. Therefore the larger the denominator of a unit fraction, the smaller the fraction.
The unit fractions of 1/2, 1/3 and 1/4 are shown on the number line below.
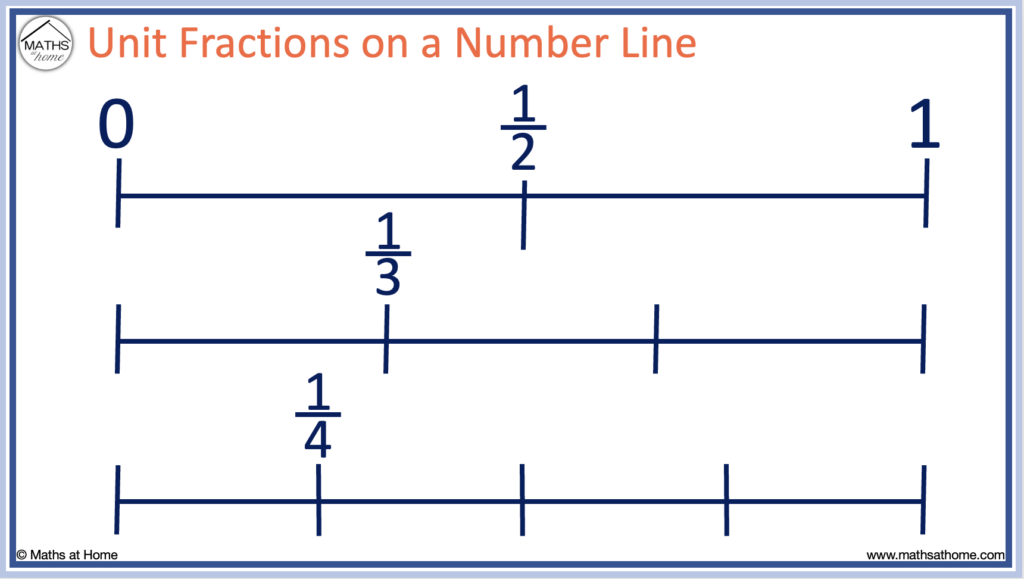
1/2 divides one whole into two equal parts.
1/3 divides one whole into three equal parts.
1/4 divides one whole into four equal parts.
1/2 is larger than 1/3 which is larger than 1/4.
How to Add and Subtract Fractions on a Number Line
To add fractions on a number line:- Divide each number on the number line into the number of parts shown on the denominator.
- Start by at the location of the first fraction.
- Count on by the number of parts shown on the top of the fraction being added.
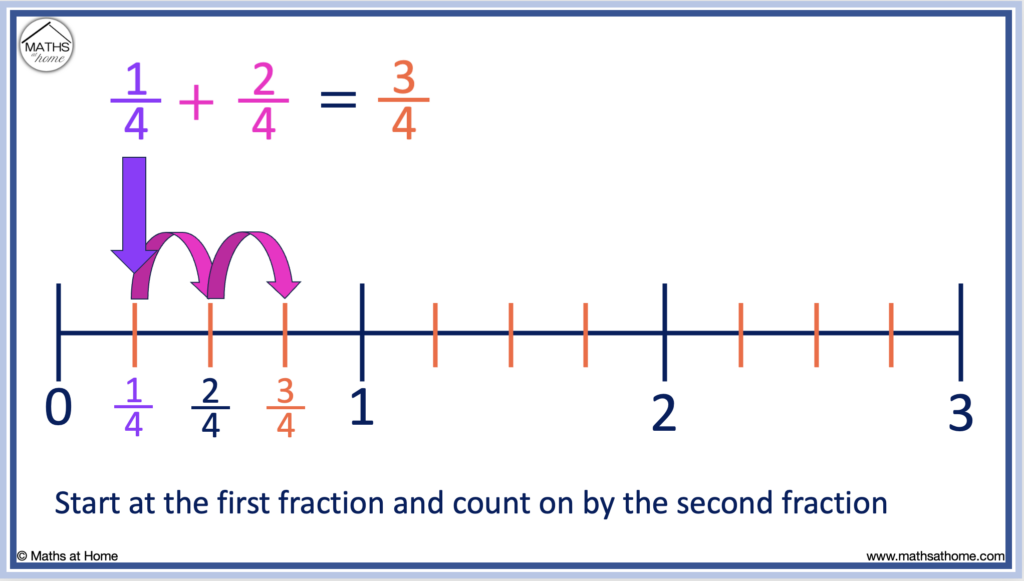
For example, add 1/4 + 2/4.
Step1. Each number on the number line is divided into four equal parts.
Step 2. The first fraction is 1/4, so we start by locating this fraction on the number line.
Step 3. We will then add 2/4, so we count on to the right by 2 more places.
We arrive at 3/4, therefore 1/4 + 2/4 = 3/4.
- Divide each number on the number line into the number of parts shown on the denominator.
- Start by at the location of the first fraction.
- Count left by the number of parts shown on the top of the fraction being subtracted.
For example, subtract the fractions 2 1/3 – 2/3.
Step 1. Divide each number on the number line into 3 equal parts.
Step 2. Start by locating the first fraction, which is 2 1/3.
Step 3. We then subtract 2/3, so we count left 2 places.
We arrive at the answer: 2 1/3 – 2/3 = 1 2/3.

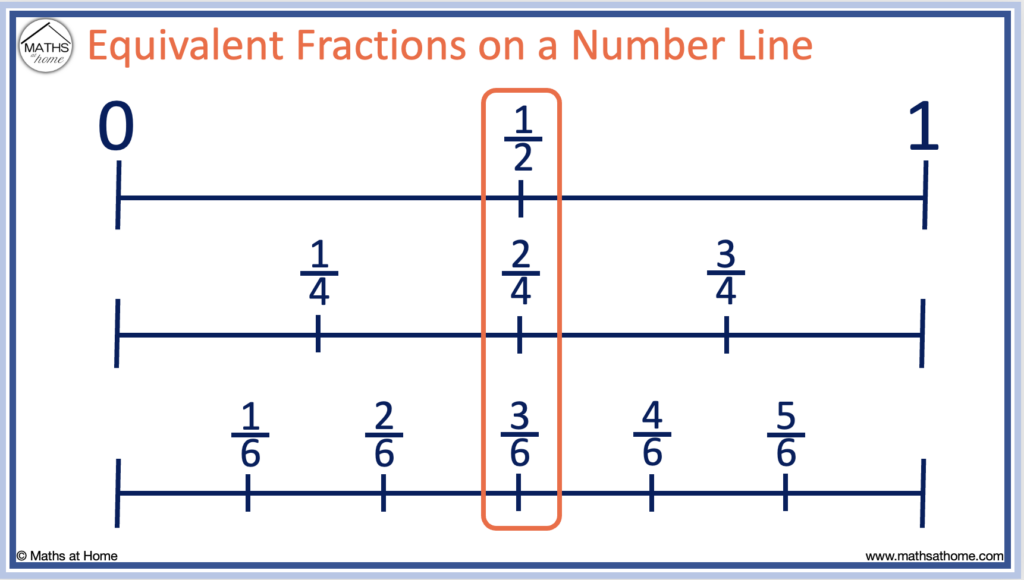
Equivalent Fractions on a Number Line
Equivalent fractions represent the same value and therefore they occupy the same position along a number line. Equivalent fractions can be seen on a number line as they will be located at the same position.
For example, 1/2 is equivalent to 2/4 and 3/6 as they all line up on a number line in the same position.
They are all located half way between 0 and 1 and so, they are all equal to one half.
Teaching Fractions on a Number Line
Using number lines to teach fractions helps to visualise their relative sizes in comparison with other numbers. They allow us to visualise fractions as part of a continuous scale rather than as a portion of a fixed set. Number lines can be particularly useful for representing addition and subtraction of fractions and fractions greater than one whole.
Why Teach Fractions using a Number Line
- Number lines allow a visual representation of the sizes of each fraction
We can see how far apart different fractions are and where fractions compare to whole numbers much more clearly on a number line.
Number lines give us a sense of scale.
- Number lines are way to find equivalent fractions
Equivalent fractions occupy the same location along a number line.
By placing number lines above one another, they can be a good way to visualise the concept of equivalent fractions.
We can count along number lines until we find fractions that are in line with others and then we can say that they are equivalent.
- Number lines are a way to represent fractions in a continuous scale
Fractions are typically taught as smaller amounts of a larger whole. We might teach one half of a shape or one tenth of a block of chocolate. Students become used to fractions only being used to represent a smaller part of a larger total.
However number lines allow students to become more familiar with fractions on any larger scale, beyond one whole.
This is useful for applying fractions to further real-life situations such as reading measuring scales, displaying time lines or representing speed or distance.
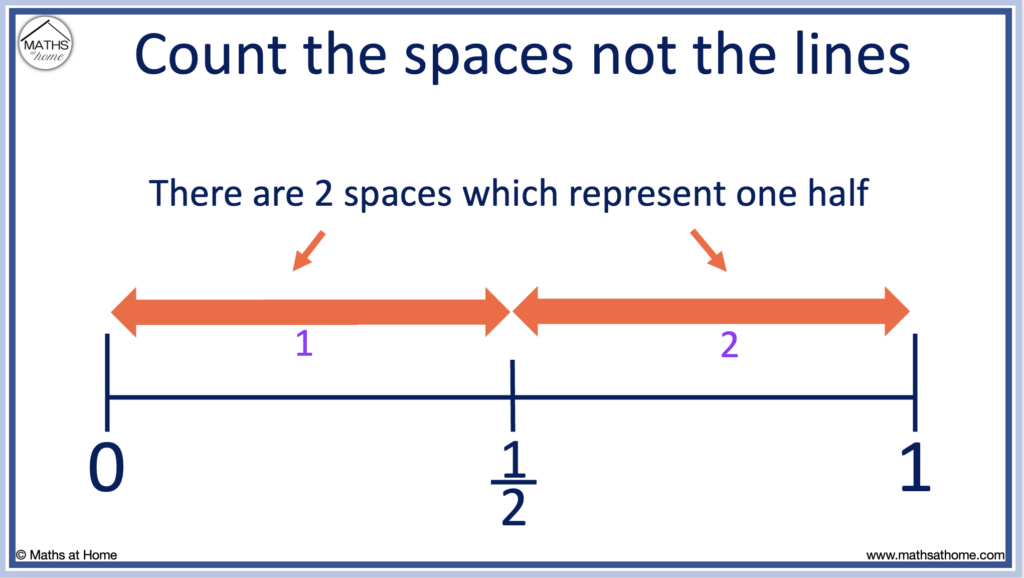
Common Misconceptions
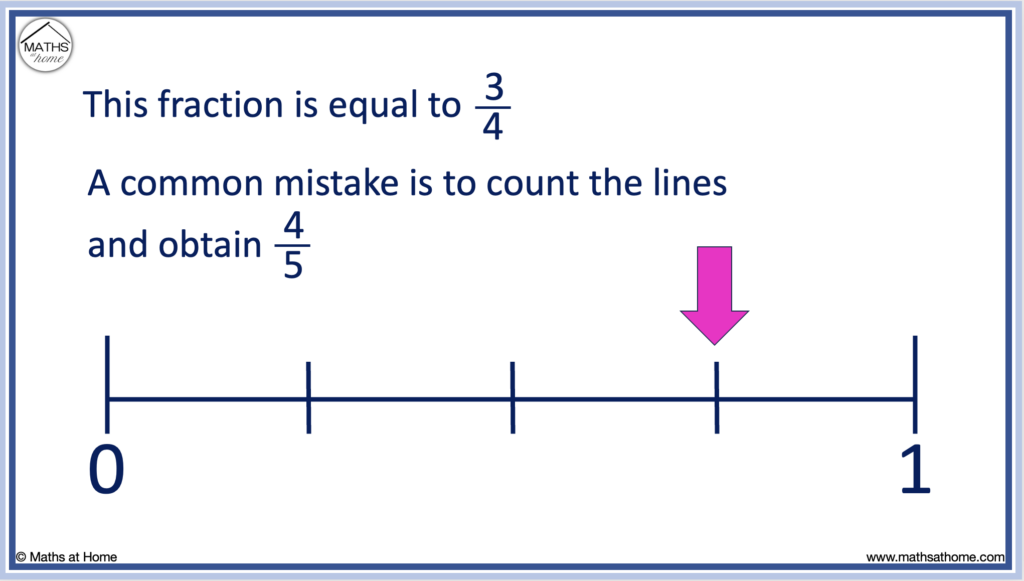
Count the spaces between each number, not the lines.
The example below shows the fraction 3/4. We have counted three of the four spaces.
Students can naturally count the lines instead of the spaces as a common misconception.
Counting the lines, they incorrectly obtain 4/5 instead of 3/4.