Video Lesson: How to Find the Equation of a Parallel Line Passing Through a Point
Parallel lines are lines that never meet (never intersect).
That is, parallel lines are oriented in the same direction. This means that they have the same gradient.
The gradient of a straight line equation (y = m𝑥 + c) is the coefficient of 𝑥. That is, the gradient is equal to the number in front of the 𝑥 when the equation is rearranged so that y is the subject. For example, the gradient of the line y = 3𝑥 + 1 is 3.
We denote the gradient with the letter m. Therefore we say in the example above that m = 3.

For example, the following lines are all parallel as they all have a gradient of 3:
- y = 3𝑥 + 1
- y = 3𝑥 + 2
- y = 3𝑥 – 5
For example, the following lines are all parallel as they all have a gradient of 2:
- y = 2𝑥 + 3
- y = 2𝑥
- y = 2𝑥 – 4
How to Find the Equation of a Parallel Line Through a Point
To find the equation of a parallel line through a given point:- Write y = m𝑥 + c where ‘m’ is the gradient of the given line.
- Substitute the 𝑥 and y values of the given point into this equation.
- Solve the resulting equation for ‘c’.
- Write y = m𝑥 + c with these known values of ‘m’ and ‘c’.
These are the steps for finding the equation of a line parallel to a given line and passing through a given point.

For example, find the equation of the line parallel to y = 2𝑥 + 3, passing through the point (3, 11).
Step 1. Write y = m𝑥 + c, where m is the gradient of the given line
The gradient of any straight line, written in the form y = m𝑥 + c, is the coefficient of 𝑥. That is, it is the number in front of 𝑥.
The original given line is y = 2𝑥 + 3.
Therefore the gradient of this line is 2. Therefore, m = 2.
Any line that is parallel to this also has a gradient of 2.
Therefore we write y = 2𝑥 + c, where c is to be found.
Step 2. Substitute the 𝑥 and y values of the given point into this equation
We are told that the parallel line, y = 2𝑥 + c, passes through the point (3, 11).
In the point (3, 11) we have 𝑥 = 3 and y = 11.
We substitute these values into y = 2𝑥 + c to obtain:
11 = 2 × 3 + c.
Step 3. Solve the resulting equation for ‘c’
11 = 2 × 3 + c can be written as 11 = 6 + c.
Subtracting 6 from both sides, we obtain 5 = c.
Therefore c = 5.
Step 4. Write y = m𝑥 + c with these known values of ‘m’ and ‘c’
We found that for this parallel line:
- m = 2
- c = 5
Therefore we write the straight line equation, y = m𝑥 + c as:
y = 2𝑥 + 5

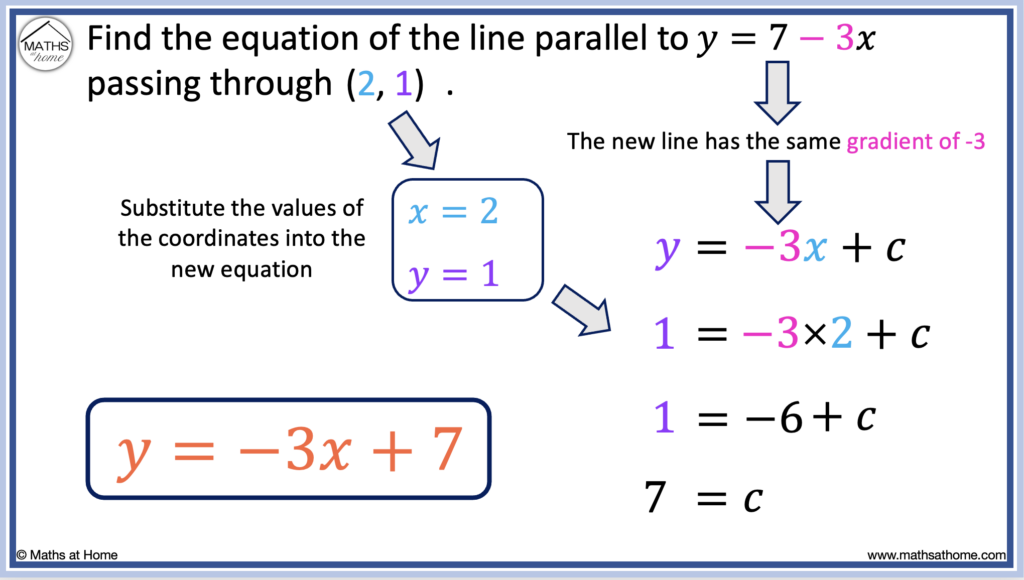
Here is another example of finding the equation of a line parallel to y = 7 – 3𝑥, passing through (2, 1).
Step 1.
The line given by y = 7 – 3𝑥 has a gradient of -3.
Any line parallel to y = 7 – 3𝑥 also has a gradient of -3.
Therefore we write y = -3𝑥 + c.
Step 2.
The line passes through (2, 1), therefore, 𝑥 = 2 and y = 1.
We substitute these values into y = -3𝑥 + c to obtain 1 = -3 × 2 + c.
Step 3.
Solving this for c:
1 = -6 + c
adding 6 to both sides of the equation, we obtain: 7 = c.
Step 4.
Now that m = -3 and c = 7, the equation y = m𝑥 + c becomes y = -3𝑥 + 7.
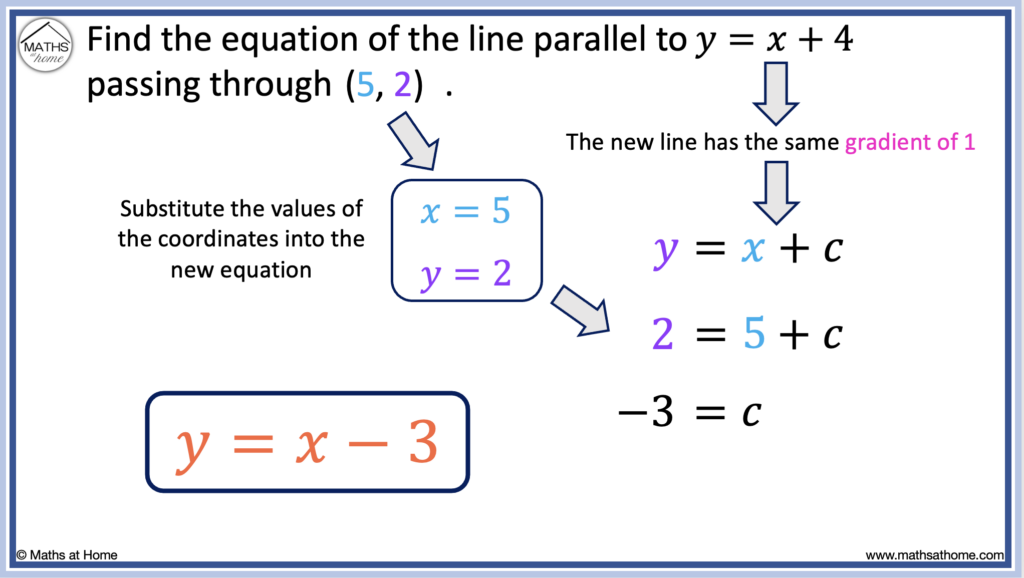
Here is another example, find the equation of the line parallel to y = 𝑥 + 4, passing through (5, 2).
Step 1.
The equation y = 𝑥 + 4 is the same as y = 1𝑥 + 4. It has a gradient of 1.
The lines parallel to this also have gradient of 1.
Therefore we write y = 𝑥 + c.
Step 2.
The line passes through (5, 2) and so, we substitute 𝑥 = 5 and y = 2 into y = 𝑥 + c to obtain:
2 = 5 + c.
Step 3.
We subtract 5 from both sides of the equation to obtain -3 = c.
Step 4.
Now that m = 1 and c = -3,
the equation y = m𝑥 + c becomes y = 𝑥 – 3.
Here is a formula for finding the equation of a parallel line through a point.
This is an alternate method that can be easier to perform mentally.
The equation of the line parallel to y = m𝑥 + k, passing through the point (𝑥1, y1), is given by y = m𝑥 + c, where c = y1 – m𝑥1.
- The gradient is the same because the lines as parallel
- Calculate the value of c using c = y1 – m𝑥1
- Substitute m and c into y = m𝑥 + c
For example, find the equation of the line parallel to y = 4𝑥 + 1, passing through the point (1, 9).
Step 1. Find m
The parallel line will have the same gradient of 4.
Step 2. Calculate c
c = y1 – m𝑥1
Therefore c = 9 – 4×1
So c = 5
Step 3. Write the equation
y = m𝑥 + c becomes y = 4𝑥 + 5.

The Point-Slope Equation of a Parallel Line Through a Given Point
The equation of the line parallel to the line y = m𝑥 + k, passing through the point (𝑥1, y1) is given by y – y1 = m(𝑥 – 𝑥1). Simply substitute the gradient of the first line as m and the coordinates of the point as 𝑥1 and y1.
The point-slope equation of a parallel line through a point
The point-slope equation gives the equation of any line provided that the gradient and a point it passes through is known.
The gradient is simply the same as the gradient of the line that it is parallel to and the point the line passes through is given.
- m = the gradient of the line
- (𝑥1, y1) are the coordinates of the point the line passes through

For example, find the equation of the line parallel to y = 2𝑥 + 5, passing through the point (3, 7).
The gradient of the line parallel to this line has the same gradient.
y = 2𝑥 + 5 has a gradient of 2 because this is the number before the 𝑥.
The line passes through the point (3, 7).
Therefore:
- m = 2
- 𝑥1 = 3
- y1 = 7

We substitute these values into the equation .
We obtain which is the equation of the line.
This can be rewritten in slope-intercept form by rearranging the equation.
Expanding the brackets, we obtain .
Adding 7 to both sides of the equation, we obtain .
Equations of Lines Parallel to the y-axis
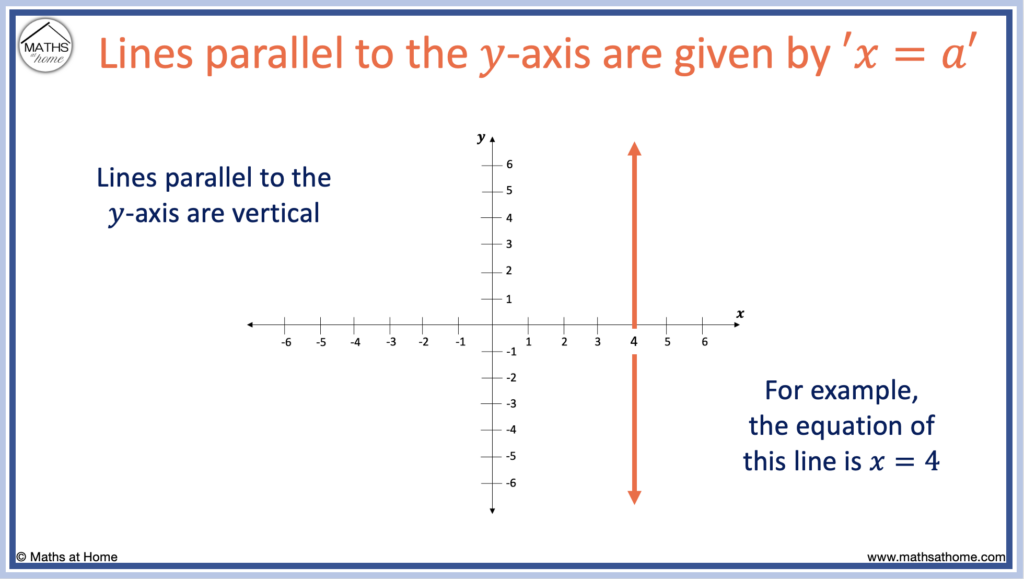
The equation of a line parallel to the y-axis is given by ‘𝑥 = a‘, where ‘a’ is the 𝑥-coordinate that the line passes through. Lines parallel to the y-axis are vertical. For example, the line parallel to the y-axis passing through (4, 0) is 𝑥 = 4.
Lines parallel to the y-axis are lines that are oriented in the same direction as the y-axis. They are vertical lines.
For example, the line below has the equation 𝑥 = 4.
Every point it passes through has an 𝑥-coordinate of 4.
For example, it passes through (4, 0), (4, 1), (4, 2) and any other point with an 𝑥-coordinate equal to 4.
Equations of Lines Parallel to the x-axis
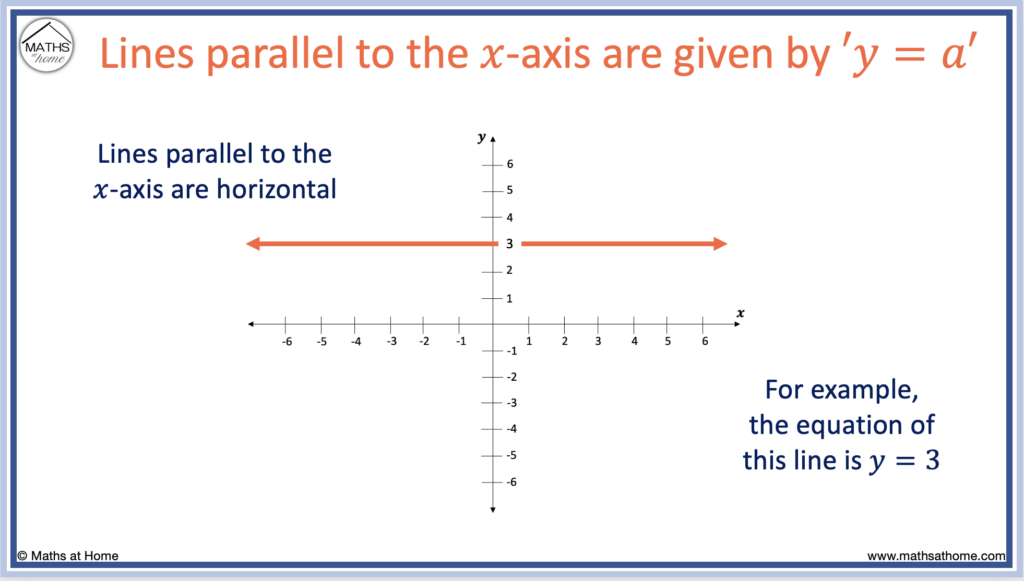
The equation of a line parallel to the x-axis is given by ‘y = a‘, where ‘a’ is the y-coordinate that the line passes through. Lines parallel to the x-axis are horinzontal. For example, the line parallel to the x-axis passing through (0, 3) is y = 3.
Lines parallel to the 𝑥-axis are lines that are oriented in the same direction as the 𝑥-axis. They are horizontal lines.
For example, the line below has the equation of y = 3.
Every point that this line passes through has a y-coordinate of 3.
For example, it passes through the points (0, 3), (1, 3), (2, 3) and any other point with a y-coordinate equal to 3.