Displacement, Velocity and Acceleration Differentiation: Video Lesson
Definitions of Displacement, Velocity, Acceleration and Jerk
Displacement is a vector quantity that is defined as the shortest distance between the initial and final position of an object. Distance is a scalar quantity and is the length of the total path taken by an object. Distance is only measured as a positive value whereas displacement is measured in both positive and negative directions.
If a car drives 10m in one direction and then immediately drives 10m in the opposite direction back to its starting location, the total distance travelled by the car will be 20m. However, the total displacement of the car will be zero as its final position is now the same as its initial location.
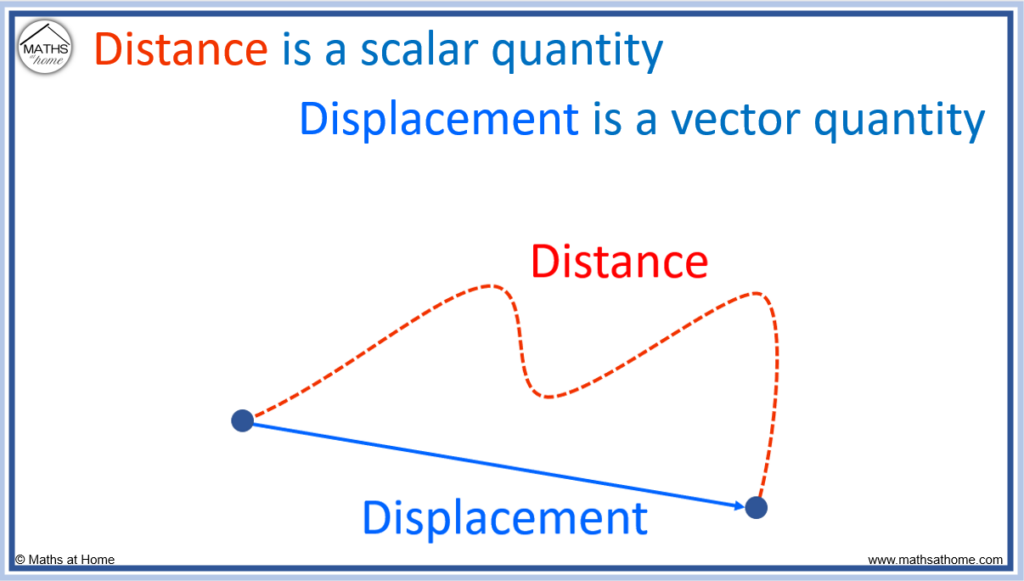
| Distance | Displacement |
| Distance is the total length of the path traveled by an object. | Displacement is the shortest distance between the initial and final position of an object. |
| Distance is a scalar quantity. It has a magnitude but no direction. | Displacement is a vector quantity which has both a magnitude and direction. |
| Distance can never be a negative value. It is only positive or zero. | Displacement can take negative, positive or zero values. |
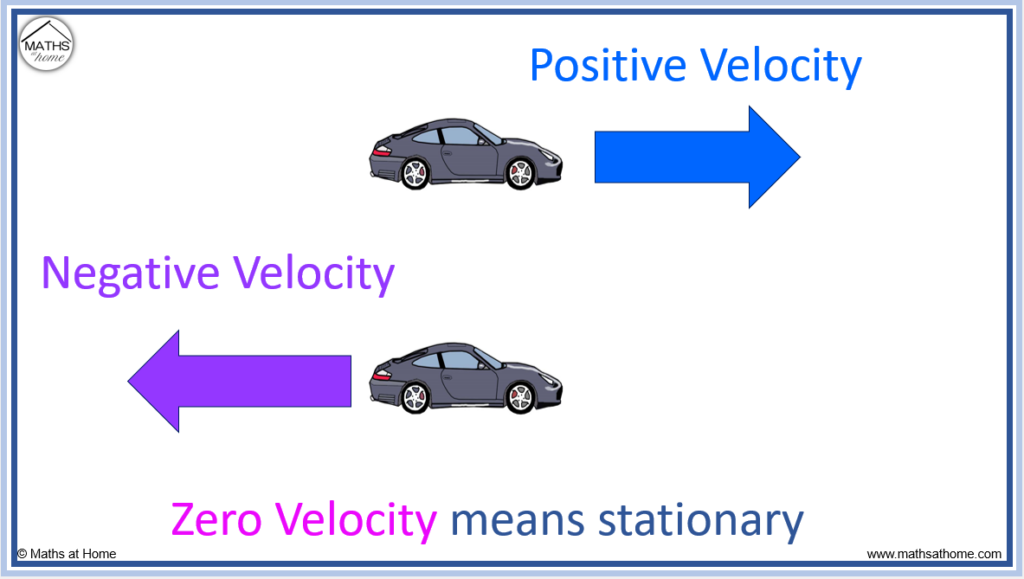
Speed is a scalar quantity and is defined as the distance travelled per unit time. Velocity is a vector quantity and is defined as the displacement travelled per unit time. Velocity must also have a direction. A negative velocity means that the object is traveling in the opposite direction to the positive direction.
Often, a positive velocity refers to an object travelling in the forwards direction, whilst a negative velocity is used to describe an object travelling in the backwards direction.
If an object has zero velocity, either it is stationary or it is reversing its direction of travel.
Speed is the rate of change of distance with time, whereas velocity is the rate of change of displacement with time.
Speed is not a vector quantity. This means that it is not described by a direction. An object travelling at 10ms-1 forwards has the same speed as an object travelling at 10ms-1 backwards. Despite having different velocities, their speeds are equal.

Acceleration is the rate of change of velocity. It is a vector quantity, which means that it has a magnitude and direction. If an object has zero acceleration, its velocity does not change.
An object undergoes acceleration if it speeds up, slows down or changes direction.
In kinematics, jerk is the rate of change of acceleration with respect to time. It is a vector quantity. Jerk is the derivative of acceleration and has the units m/s3.
Jerk is the third derivative of displacement with respect to time. Snap, crackle and pop are the fourth, fifth and sixth derivatives of displacement respectively. Snap, crackle and pop are named after the Rice Krispies mascots and have little practical use.
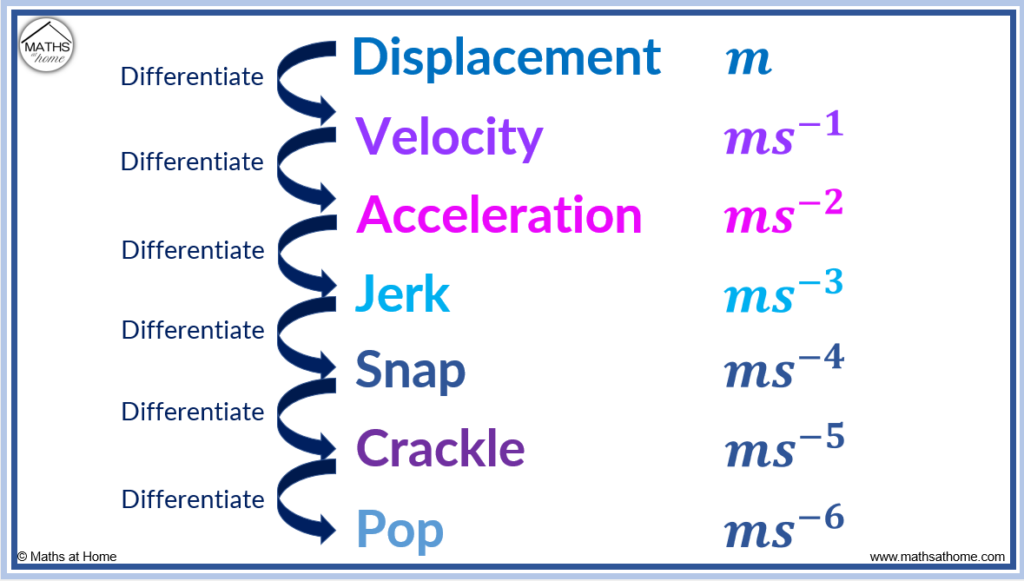
The standard units of displacement are metres (m). Velocity has the units of metres per second (ms-1) and acceleration has the units of metres per second squared (ms-2).
The Relationship Between Displacement, Velocity and Acceleration
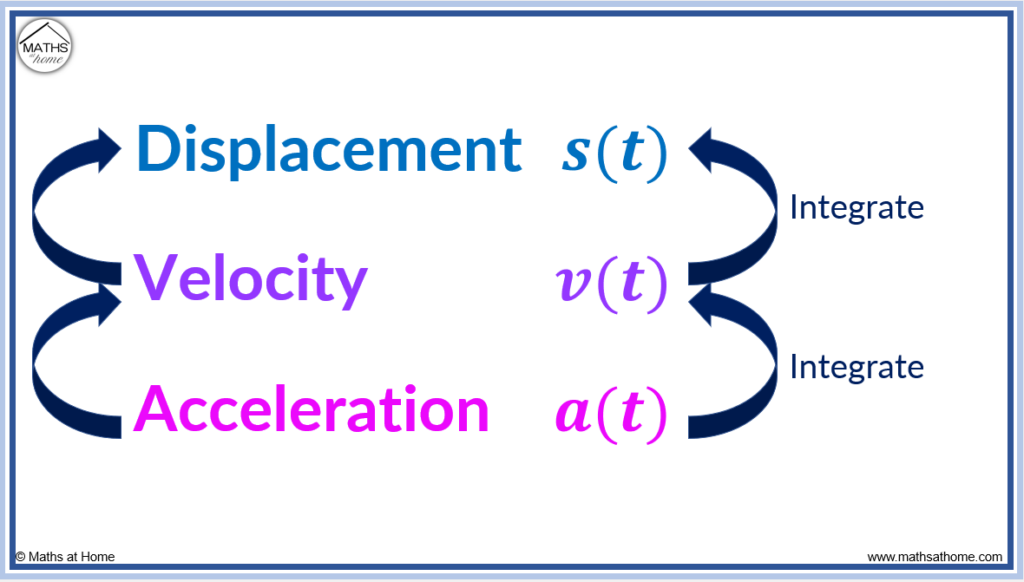
The equation for the instantaneous velocity of a particle can be found by differentiating the displacement equation with respect to time. The equation for the instantaneous acceleration of a particle can be found by differentiating the velocity equation with respect to time. Velocity is the first derivative of displacement and acceleration is the second derivative.
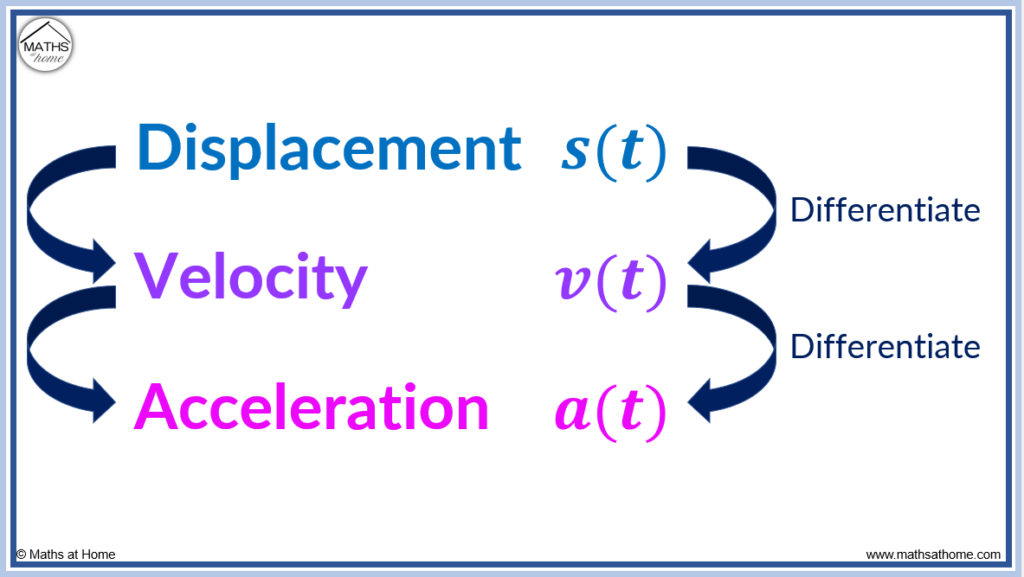
How to find Velocity and Acceleration by Differentiating Displacement
Example 1: The displacement of a particle from an origin is given by , where t is the time in seconds.
Find expressions for the velocity and acceleration.
The velocity equation is found by differentiating the displacement equation with respect to time.
The displacement equation is .
Differentiating, the velocity equation is .
The acceleration equation is found by differentiating the velocity equation with respect to time.
Differentiating, the acceleration equation is .

Find the velocity after 2 seconds
Since velocity is required, the velocity equation of is considered.
We simply substitute t=2 into this equation to find the velocity after 2 seconds.
Example 2: The displacement of a a particle from an origin is given by , where t is the time in seconds.
Find expressions for the velocity and acceleration.
Differentiating the displacement equation with respect to time, .
Differentiating the velocity equation with respect to time, .

Find the displacement when the acceleration is 16ms-2.
In this question, we first must find the time at which the acceleration is equal to 16.
and so, setting the acceleration to 16 we obtain
.
Solving for time, we obtain t = 2 seconds. Therefore the acceleration is 16ms-2 after 2 seconds.
Now we substitute t=2 into the displacement equation to obtain the answer.
and
which equals 6m.
Finding Displacement by Integrating Velocity
To find the displacement equation, integrate the velocity equation with respect to time. The constant of integration can be found by substituting any initial conditions into the displacement equation.

Example 1: The velocity of a particle is given by . Find the equation for the displacement of the particle if it was at the origin initially.
The displacement of the particle is found by integrating the velocity equation.
and so,
.
Therefore the displacement is given by , where C is the constant of integration.
To find the value of C, we substitute in a known displacement. We know that the particle was at the origin initially. This means that the displacement was zero when the time was zero.
Substituting s(0)=0, the equation becomes
and so, C= 0.
Therefore the displacement equation is just m.

Find the displacement after 1 second.
In this question, we simply substitute a time of t=1 into the displacement equation that we have just found.
and so,
.
and so, the displacement is 4 metres after 1 second.
Example 2: Find the displacement of a particle with acceleration if it is initially 2 m to the right of the origin, travelling at 1ms-1.
To find the velocity, integrate the acceleration equation. .
and so,
.
We know that the particle is moving 1ms-1 when the time equals zero.
and therefore,
.
The velocity equation is .

To find the displacement equation, integrate the velocity equation.
and so,
.
.
We know that the particle starts 2 metres away from the origin initially. This means that when time equals zero, the displacement is 2.
Therefore and so,
.
Therefore the displacement equation is .
Displacement from the Velocity-Time Graph
The displacement of an object is equal to the area between the line of a velocity-time graph and the axis. Where the graph is above the axis, the displacement is positive. Where the graph is below the axis, the displacement is negative.
For example, the displacement can be found for the velocity-time graph below by finding the area between the graph and the time axis.
The displacement is the integral of velocity. The area under a curve is found using integration. Therefore the area under the velocity time graph is equal to the displacement.
- In the first 4 seconds, the area is the area of a triangle with a base of 4 and a height of 5.
and so, the displacement in the first 4 seconds is 10 metres.
- Between 4 and 10 seconds, the area is the area of a rectangle with base 6 and height 5.
and so, the displacement between 4 and 10 seconds is 30 metres.
Between 10 and 16 seconds, the area is the area of a rectangle with base 6 and height 3.
and because this rectangle is below the time axis, this displacement is negative. The displacement between 10 and 16 seconds is -18 metres.
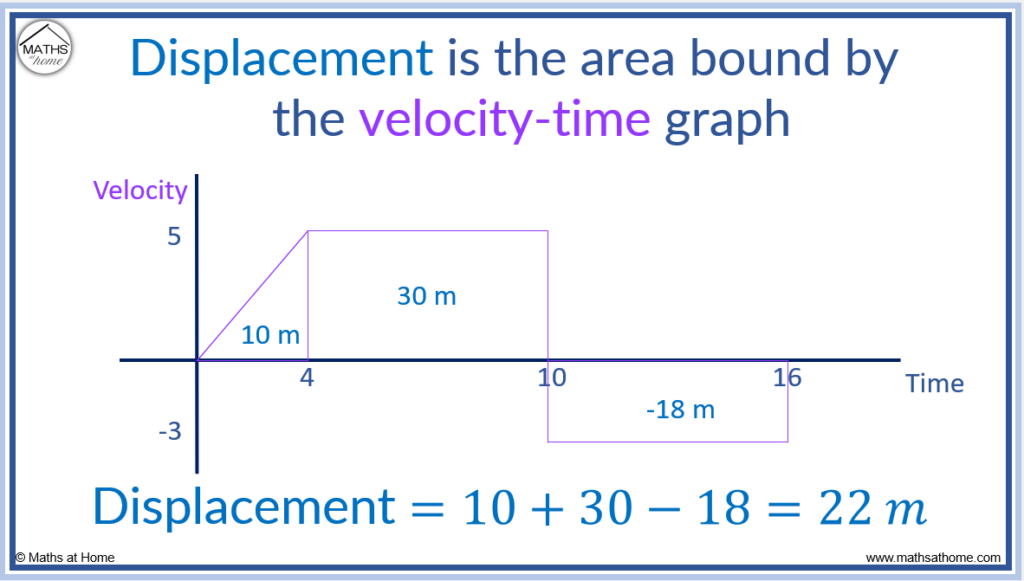
The total displacement from 0 to 16 seconds is found by finding the sum of the areas from 0 to 16.
10 + 30 – 18 = 22 and so, the displacement is 22 metres.
The object moved forwards 10 metres then moved forwards a further 30 metres before reversing 18 metres.
Acceleration from the Velocity-Time Graph
The acceleration of an object is given by the slope of the velocity-time graph. The size of the gradient between two points on a velocity-time graph is equal to the average acceleration over this time period. The instantaneous acceleration at a particular time is equal to the gradient of the tangent to the velocity-time graph at this point.
The gradient is calculated as rise over run.
Acceleration is the derivative of velocity. The gradient of a graph is found using differentiation. Therefore the gradient of the velocity-time graph is equal to the acceleration.
For example, in the first 3 seconds of the velocity-time graph below, the rise is 6 and the run is 3.
and so, the acceleration in the first 3 seconds is 2ms-2.
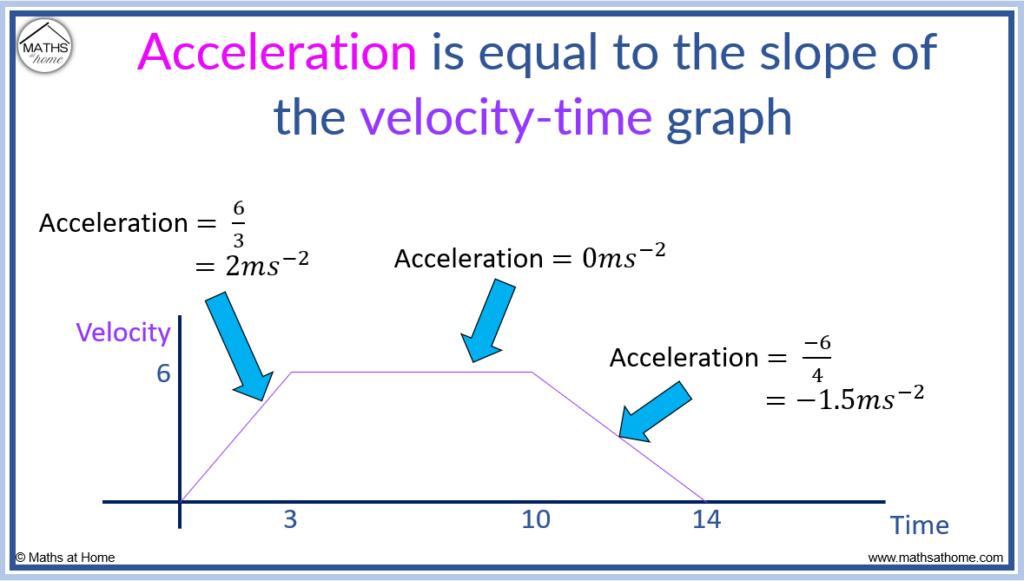
In the time from 3 to 10 seconds, the acceleration is zero because the gradient is zero.
For the regions where the velocity-time graph is horizontal, the acceleration is zero. This is because the gradient is zero.
In the region from 10 to 14 seconds, the rise is -6 and the run is 4.
and so, the acceleration between 10 and 14 seconds is -1.5ms-2.
Formulae for Displacement, Velocity and Acceleration
The formula linking displacement, velocity and acceleration is s=vt-1/2at2, where s is displacement, v is velocity and a is acceleration. This formula works provided the acceleration is constant.
The equations of motion linking displacement (s), velocity (v), acceleration (a), initial velocity (u) and time (t) are:
- v=u+at
- s=ut+1/2at2
- v2=u2+2as
- s=1/2(u+v)t
- s=vt-1/2at2
How to Find Where a Particle Changes Direction
A particle changes direction at the positions where v=0 and a≠0. Set the velocity equation equal to zero and solve for time. If the acceleration at these times is zero, then the particle is stationary. If the acceleration is not equal to zero, then it is changing direction.
For example, the displacement of a particle from an origin is given by , where t is the time in seconds.
Find the displacement when the particle changes direction.
1. Find the expression for velocity by differentiating the displacement equation.
2. Set the velocity equation to zero and solve for time
0=2t-6 and so, t=3 seconds.
The particle reverses direction after 3 seconds.

To find the displacement of the particle when it changes direction, substitute the time of t=3 into the displacement equation.
and so,
.
This equals -5 and so, the particle is located at -5 metres from the origin when it turns around.
