How to Read a Binary Number: Video Lesson
How to Write a Number in Binary: Video Lesson
How to Read Binary
To read a binary number:
- Write a 1 above the rightmost binary digit.
- Write a 2 above the next digit to the left and a 4 above the next digit.
- Keep doubling the number written above as you move one digit to the left.
- Add the numbers that are above the binary digits that contain a 1.

Example of Reading a Binary Number of 1011
We will use these steps to read the binary number of 1011.
Step 1. Write a 1 above the rightmost binary digit
The image below shows a 1 written above the rightmost digit of the binary number.

Step 2. Write a 2 above the next digit to the left and a 4 above the next digit
We write a 2 next to the 1 that was written previously.
We write a 4 next to this 2 as we move left.

Step 3. Keep doubling the number written above as you move one digit to the left
We have already written 1, 2 and 4 above the digits.
We have doubled 1 to get 2, doubled 2 to get 4 and now we double 4 to get 8.
We write an 8 above the next digit to the left.

Step 4. Add the numbers that are above the binary digits that contain a 1
In the binary digit of 1011, there are three digits of 1.
Above these ones, we have written a 1, 2 and an 8.
We add 8 + 2 + 1 = 11 to see that the binary number of 1011 is the number 11 in decimal form.

We did not add the 4 because this was above the 0.
In binary, a 1 means that we use the digit written above the number and a 0 means that we do not use it.
Examples of Reading Binary Numbers
Read the binary number: 10001.
Write the powers of 2 from right to left above the digits of the binary number. This is 16, 8, 4, 2, 1.
Add the powers of two that have a binary digit of 1 below them.
Here we have a 1 below 16 and 1, so we add 16 and 1 to get an answer of 17.
10001 is the binary way of writing the number 17.

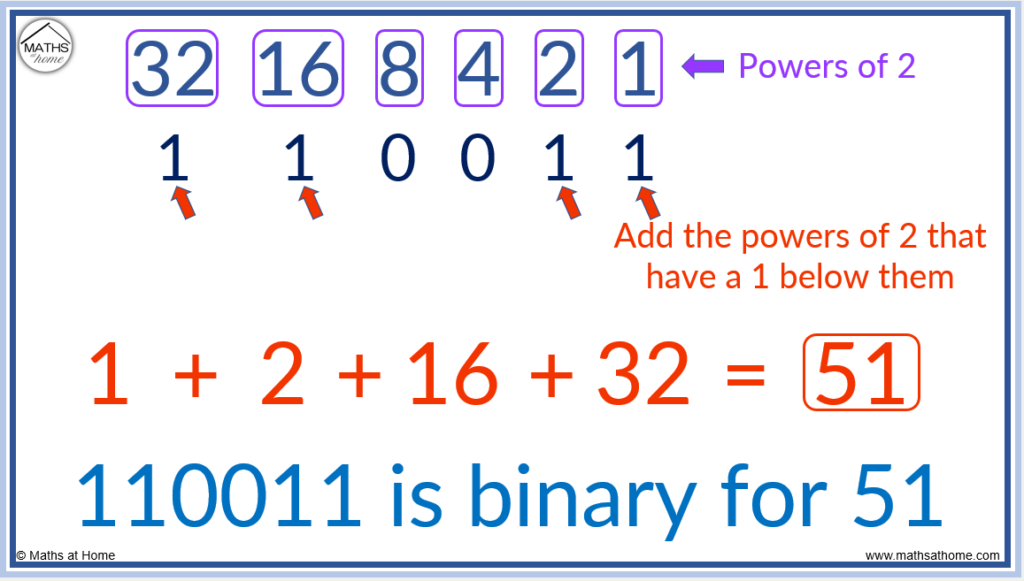
For example, read the binary number of 110011.
The powers of two are written above the digits from right to left, starting with 1 on the right.
32, 16, 8, 4, 2, 1.
Add the powers of 2 that have a binary digit of 1 below them. That is 32, 16, 2 and 1.
1 + 2 + 16 + 32 = 51 and so, 110011 is the binary number that represents 51.
Binary numbers always start with a leading digit on the left hand side of 1. Binary numbers never start with a 0.
Even binary numbers always end in a 0. If a binary number ends in a 0, it is even.
Odd binary numbers always end in a 1. If a binary number ends in a 1, it is odd. This is because the digits of binary numbers represent powers of 2. The only odd power of 2 is the final binary digit of 1.
Here are some examples of converting binary to decimal numbers.
| Binary Number | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | Sum | Decimal Number |
| 101 | 1 | 0 | 1 | 4 + 1 = | 5 | |||||
| 111 | 1 | 1 | 1 | 4 + 2 + 1 = | 7 | |||||
| 1010 | 1 | 0 | 1 | 0 | 8 + 2 = | 10 | ||||
| 10100 | 1 | 0 | 1 | 0 | 0 | 16 + 4 = | 20 | |||
| 101011 | 1 | 0 | 1 | 0 | 1 | 1 | 32 + 8 + 2 + 1 = | 43 | ||
| 1010101 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 64 + 16 + 4 + 1 = | 85 | |
| 10110100 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 128 + 32 + 16 + 4 = | 180 |
How to Write a Number in Binary
To write a number in binary, first write powers of 2 from right to left. For example: 16, 8, 4, 2, 1. Then place a 1 below the powers of 2 that add to make the number. Place a 0 below any powers of 2 that are not used. For example, 19 in binary is 10011 because the 5 digits of 10011 represent 16, 8, 4, 2 and 1 and the 16, 2 and 1 add to make 19.
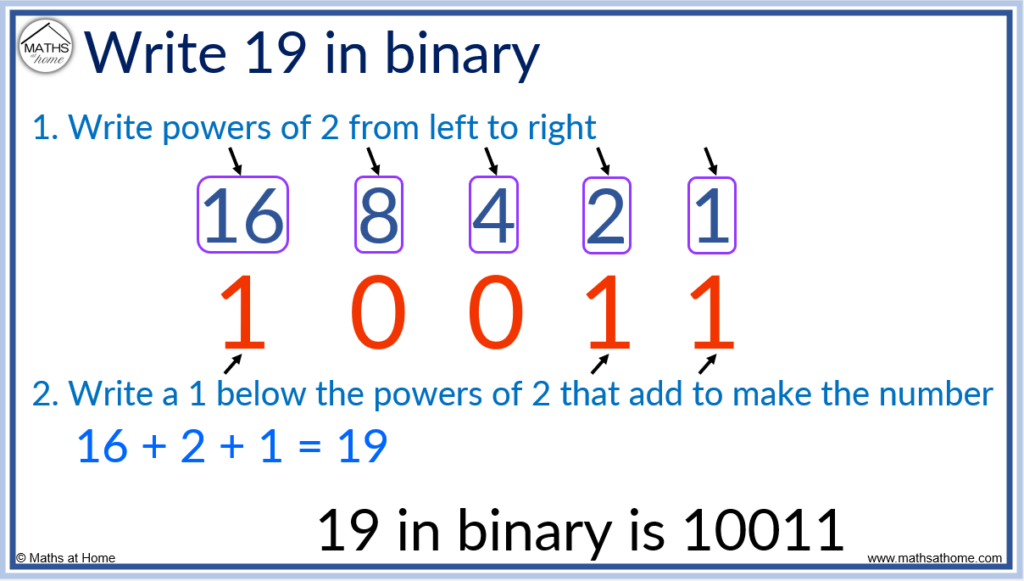
For example, convert the decimal number of 50 into binary.
The powers of 2 are written above the binary number. We start with a 1 on the right and double as we go left.
We have 32, 16, 8, 4, 2, 1.
Now we select the powers of 2 from this list that add to make 50. That is 32 + 16 + 2.
We write a 1 below the 32, 16 and 2 columns and a 0 below the numbers that we did not use. We did not use an 8, 4 or 1, so we put a 0 in these columns.
50 in binary is 110010.

To convert a larger number to binary:
- Subtract the largest power of 2 possible from the number
- Write a 1 in the place value column below this power of 2
- Subtract the largest power of 2 possible from the remainder
- Write a 1 in the place value column below this power of 2
- Continue doing this until there is a remainder of 0
- Write a 0 in the place value columns below the powers of 2 not used
For example, convert 150 to binary.
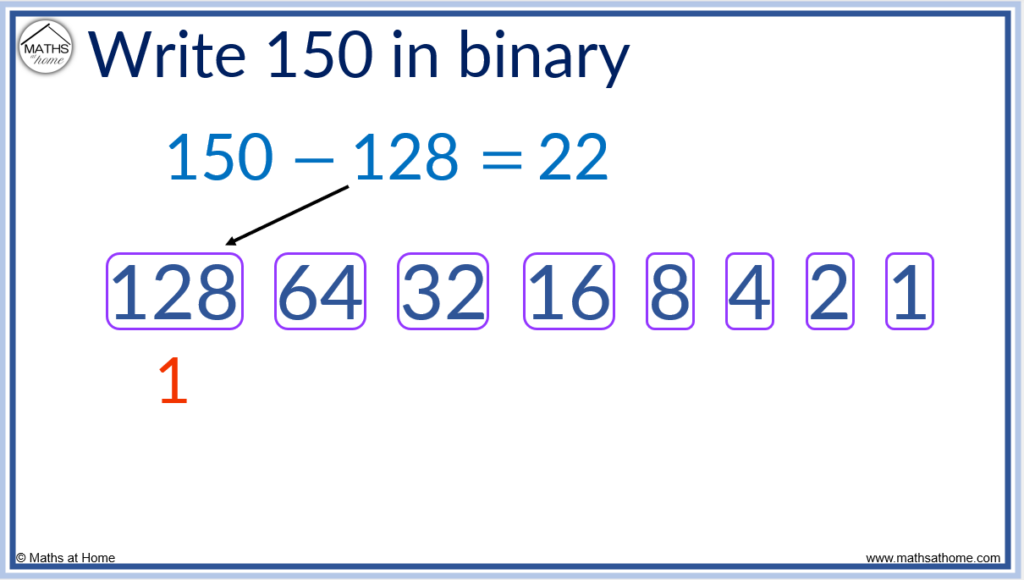
Step 2. Write a 1 below 128.
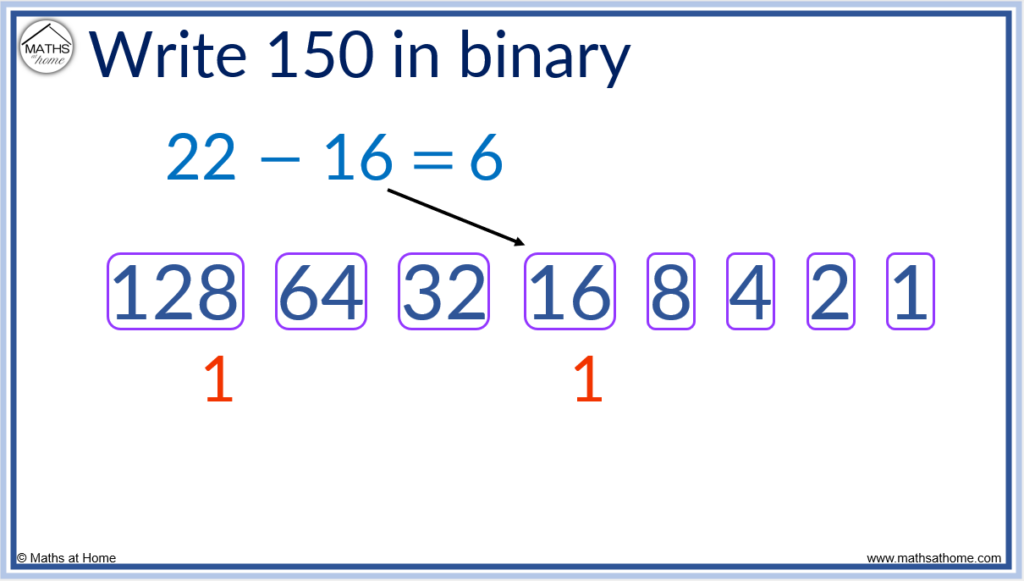
Step 4. Write a 1 below the 16.
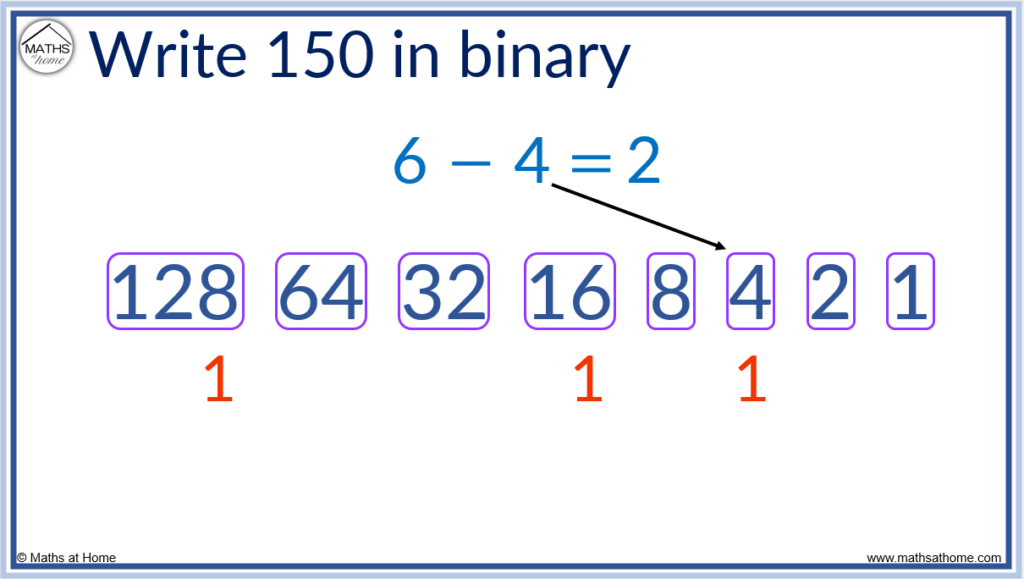
Subtract 4 from 6 to leave a remainder of 2.
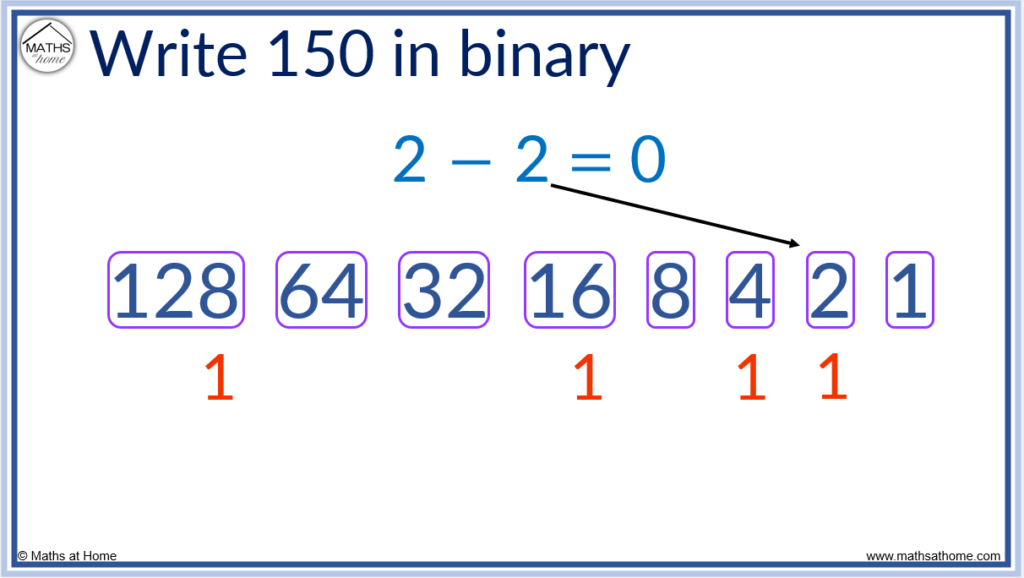
Subtracting 2 from the remainder of 2 gives us a remainder of zero.
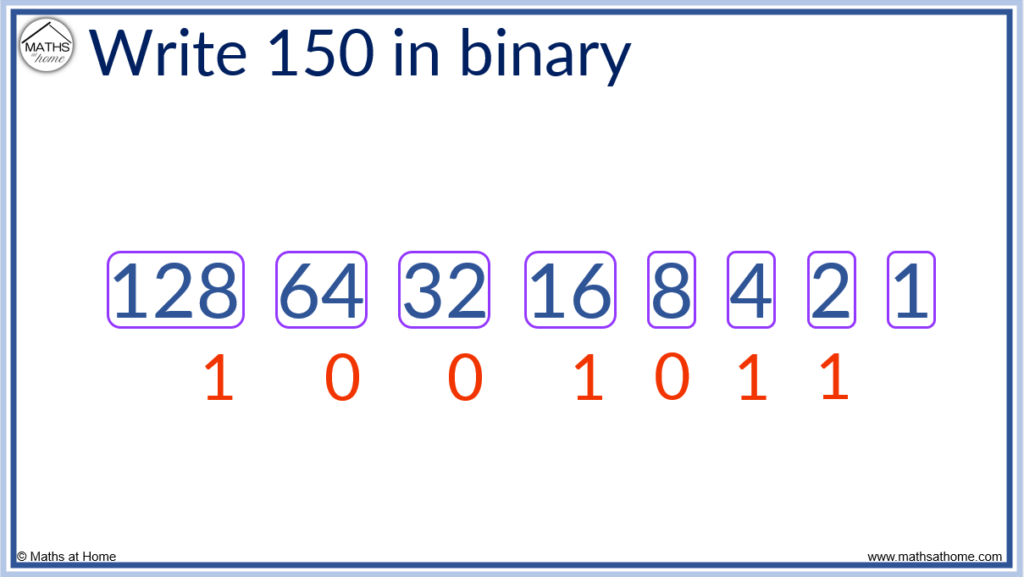
We did not subtract 64, 32 or 8 in this process and so, we write a 0 in these place value columns.
150 in binary is 1001011.
List of Binary Numbers
The first ten binary numbers are 1, 10, 11, 100, 101, 110, 111, 1000, 1001 and 1010.
Here is a list of binary numbers from 1 to 100.
| Number | Binary Number |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
How to Write a Decimal Number in Binary
In binary, the value of the digits to the left of the decimal point double as you go left. The value of the digits to the right of the decimal point halve as you go right. For example in the binary number 101.1, the place value columns represent 4, 2, 1 and then 0.5. Therefore 101.1 = 4 + 1 + 0.5, which is equal to 5.5.
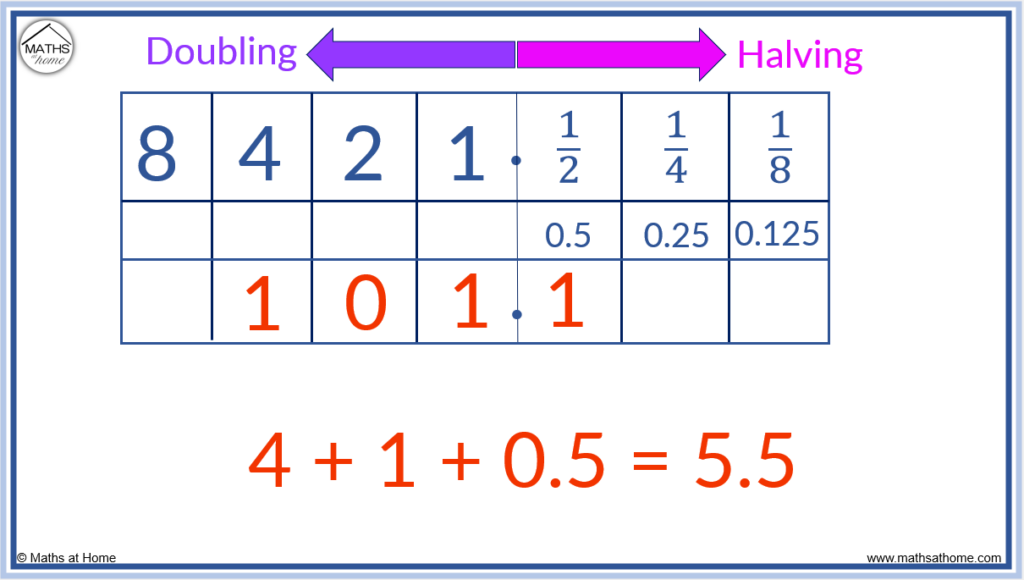
Here is a binary number with a decimal point: 0.11.

