Prim’s Algorithm: Video Lesson
How to do Prim’s Algorithm
To do Prim’s Algorithm:
- Start at any node.
- Join this node to its nearest node.
- Join any of the connected nodes to the nearest unconnected node.
- Continue joining unconnected nodes in this way until all nodes are connected.

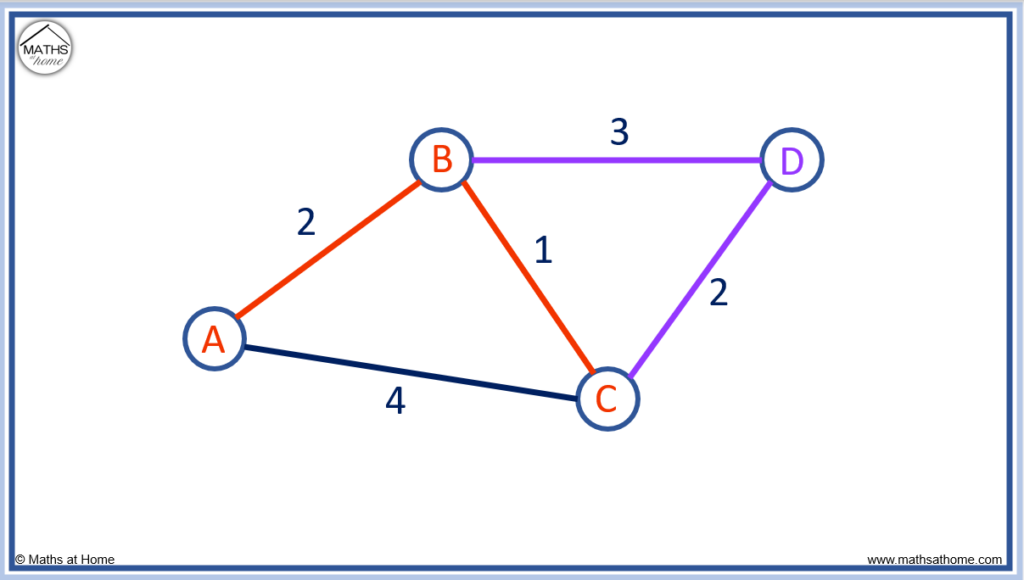
For example, use Prim’s Algorithm to find the minimum spanning tree for this network.
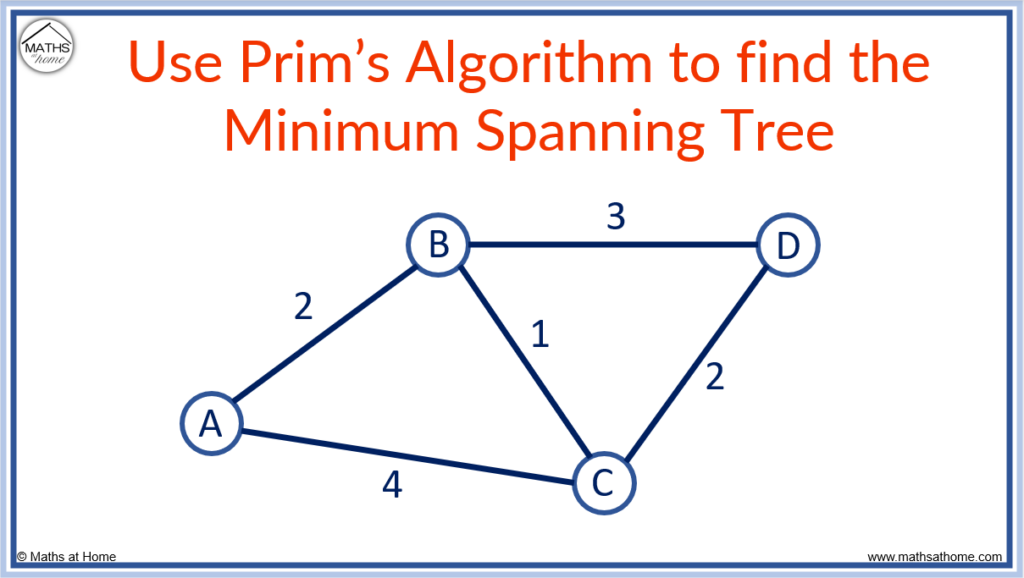
Step 1. Start at any node
We can choose any node we like, so we will consider node A.
Step 2. Join this node to its nearest node
From node A, we can travel 2 to get to node B or 4 to get to node C.
2 is less than 4 and so, the nearest node is B.
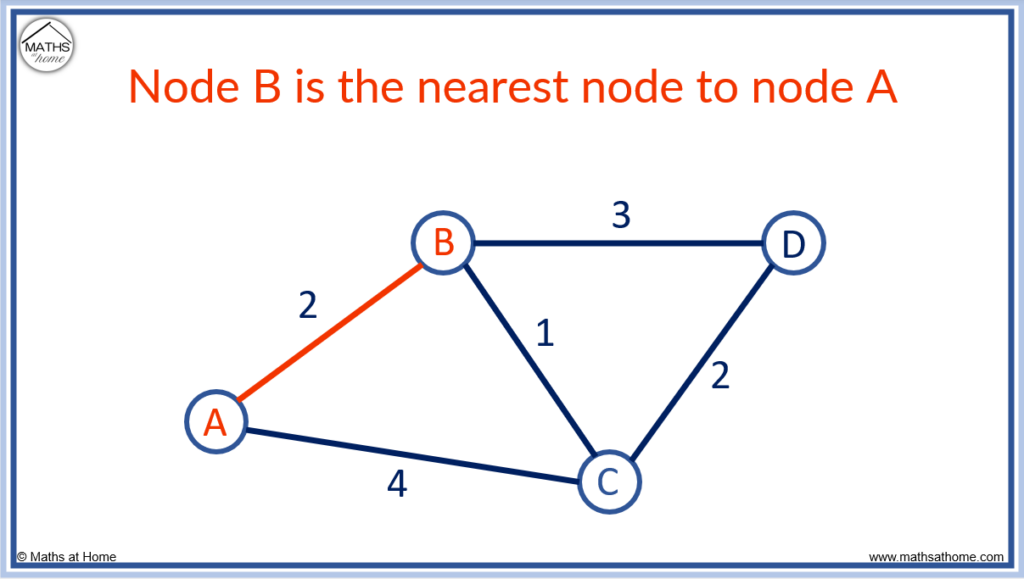
Nodes A and B are now connected nodes
Step 3. Join any of the connected nodes to the nearest unconnected node
A and B are currently the connected nodes.
We can connect nodes C and D in the following ways.
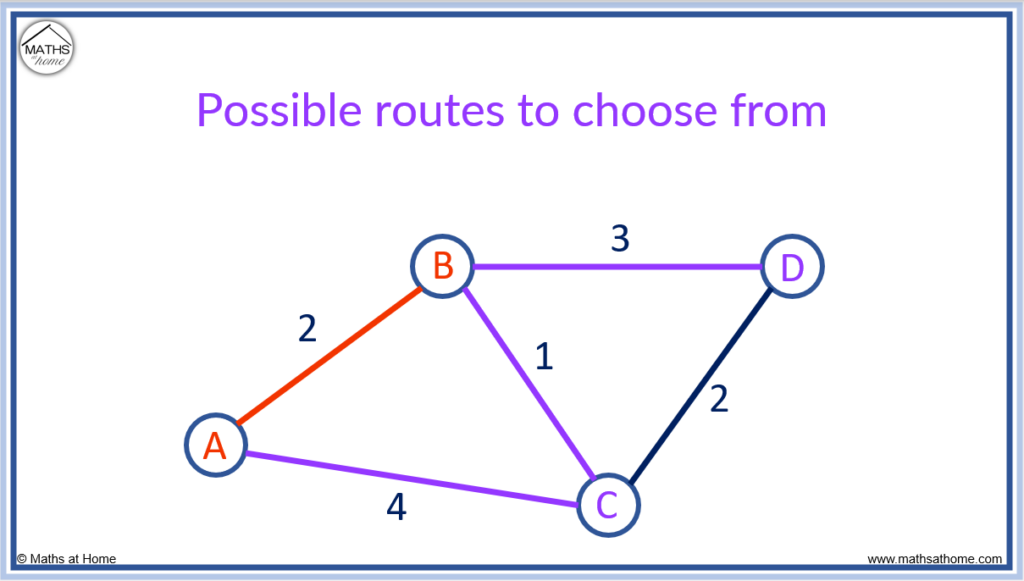
We need to select the nearest node. That is, the smallest number out of these options.
The smallest number is 1 and so, the route from B to C is chosen.
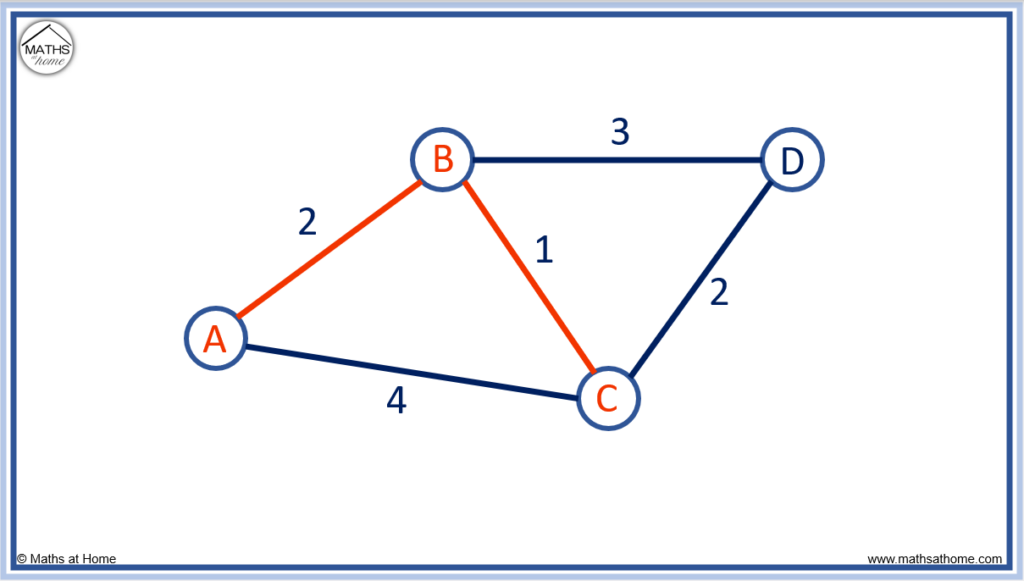
Step 4. Continue joining unconnected nodes in this way until all nodes are connected
We have now connected nodes A, B and C. Node D remains unconnected.
We can connect node D in the following ways.
We always choose the shortest route, which here is 2.
Prim’s algorithm is complete once all of the nodes are connected.
To find the length of the minimum spanning tree, add up the numbers on the edges connecting the nodes.
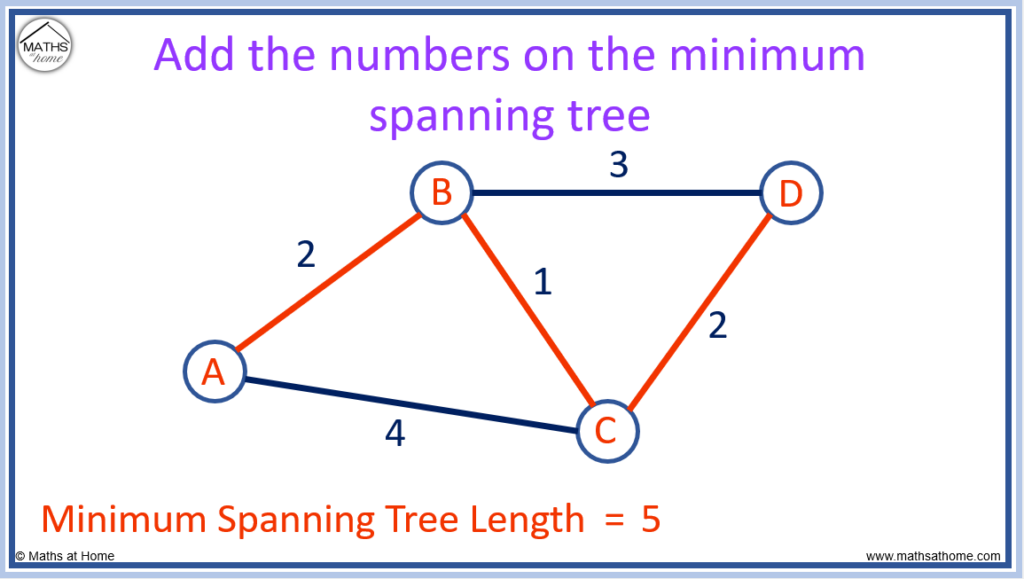
The numbers on the edges of the completed tree are 2, 1 and 2.
2 + 1 + 2 = 5 and so, the length of the minimum spanning tree is 5.
Example of Prim’s Algorithm to Find the Minimum Spanning Tree
Here is an alternate way of explaining Prim’s algorithm.
Prim’s algorithm:
- Pick a node and connect it to its nearest node.
- Examine the connected nodes and connect them to the nearest unconnected node.
- Repeat step 2 until all nodes are connected.
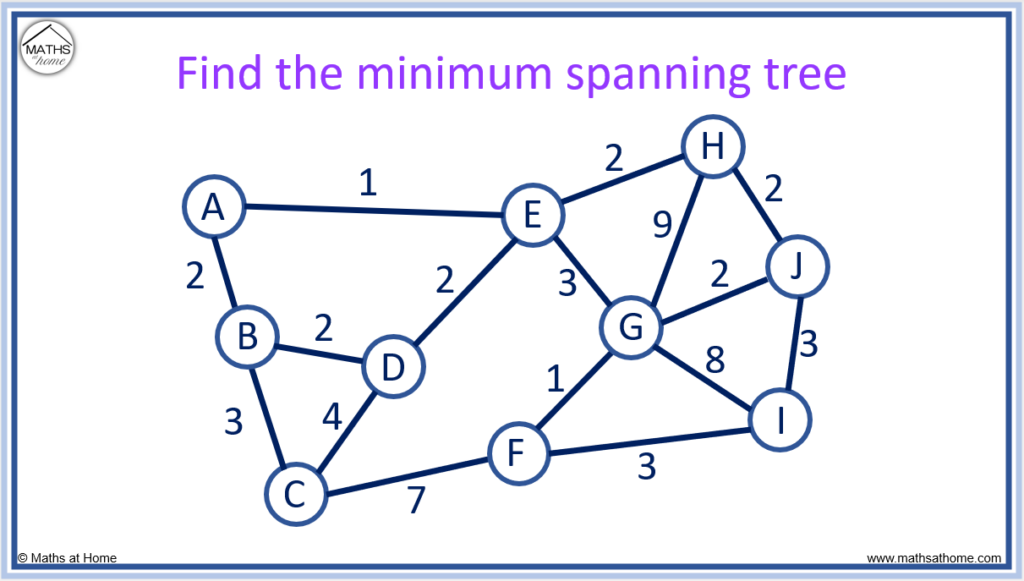
Use Prim’s algorithm to find the minimum spanning tree of the following graph.
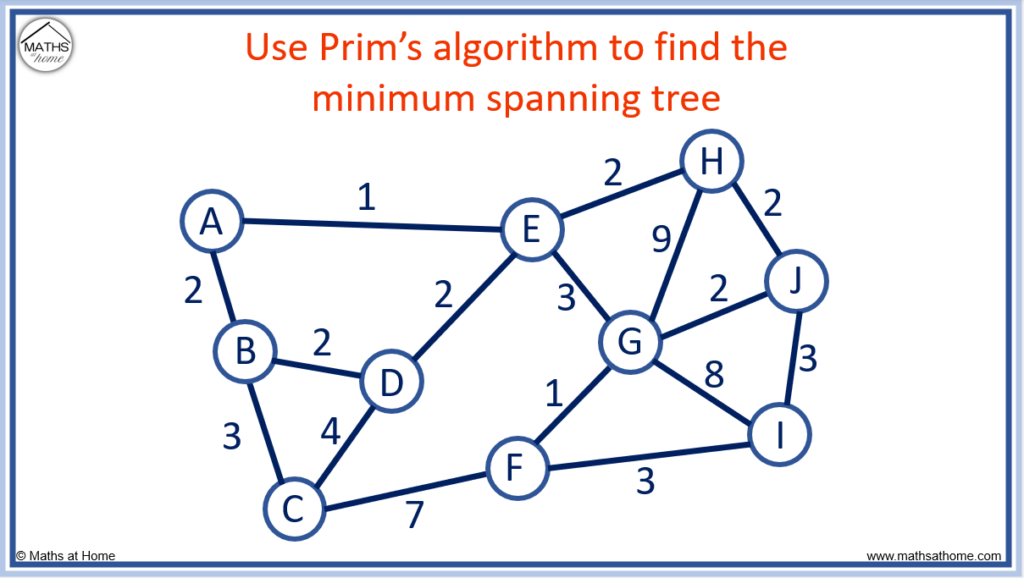
Step 1. Pick a node and connect it to its nearest node
We can pick any node, so we pick node A.
From node A, we can travel to node B or node E.
Node A to node B has an edge length of 2.
Node A to node E has an edge length of 1.
We connect A to E as this is the shortest edge.
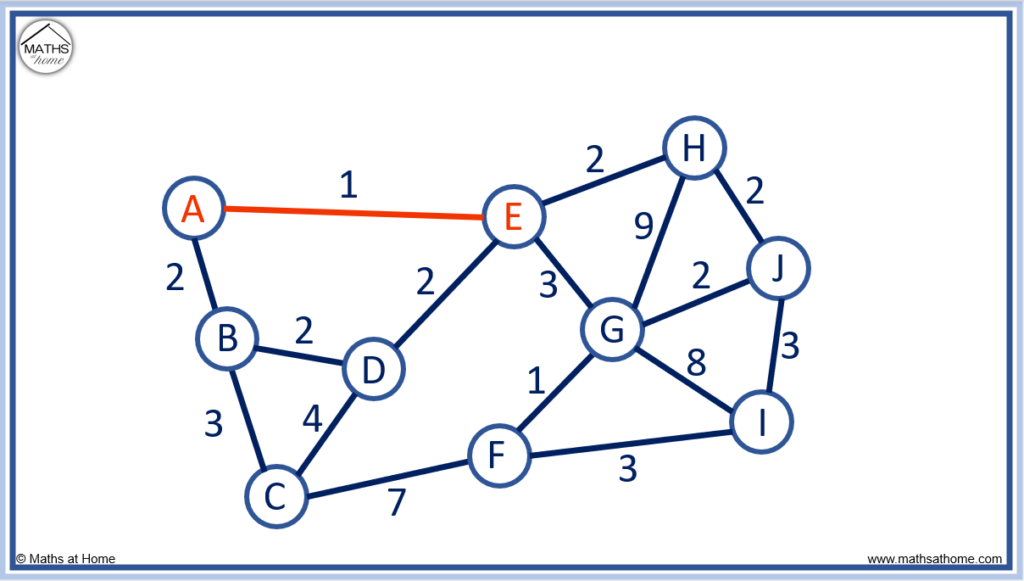
Step 2. Examine the connected nodes and connect them to the nearest unconnected node
The node of A and E are our connected nodes.
Below, the possible routes from A and E are shown below in purple. We look for the shortest route with the smallest number.
- A to B has an edge length of 2
- E to D has an edge length of 2
- E to G has an edge length of 3
- E to H has an edge length of 3
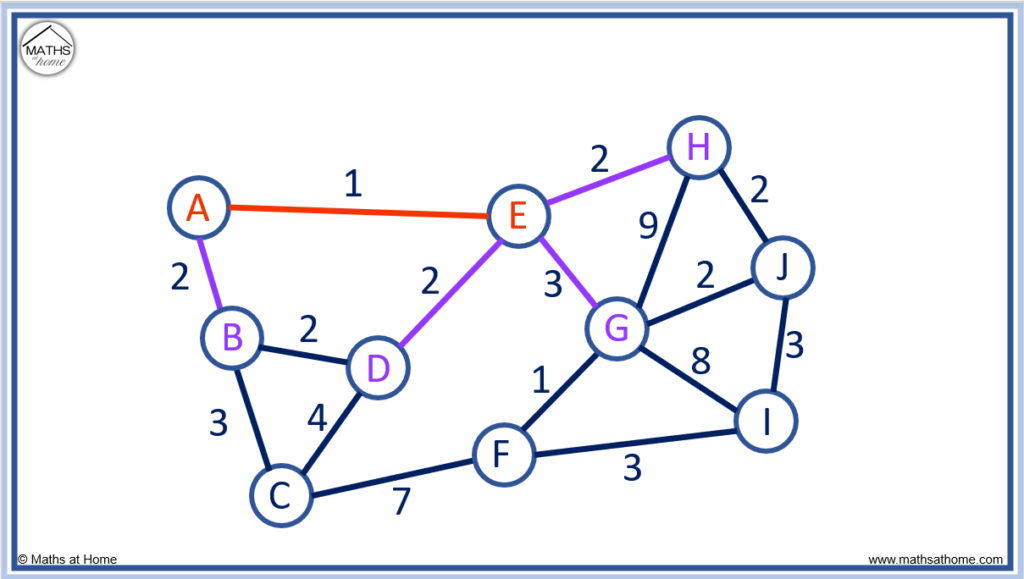
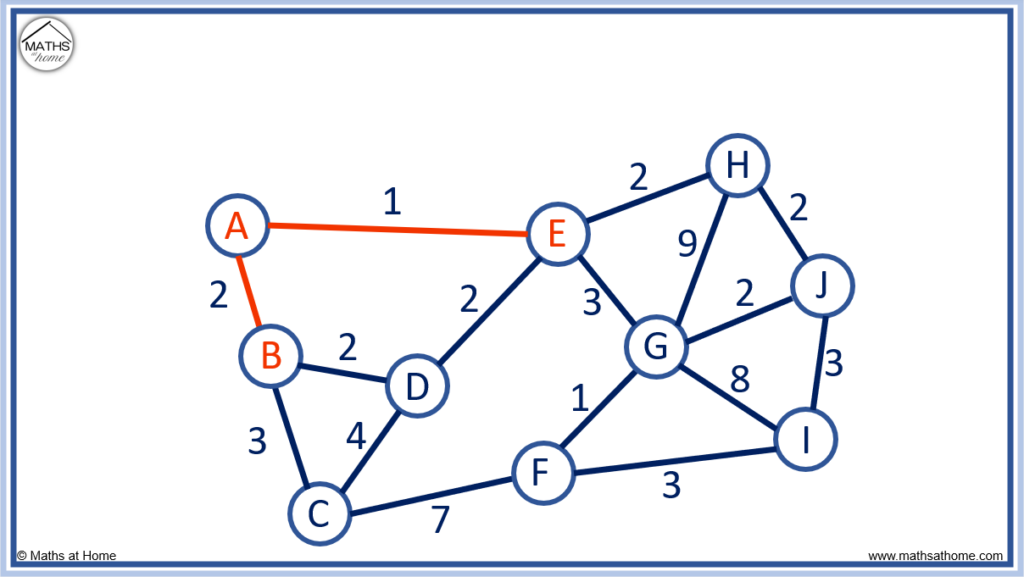
We can see that the shortest edge length we can choose from is 2.
In Prim’s algorithm, if 2 or more nodes are equally far away, choose any of them.
We will choose the first path from A to B as shown above in red.
It does not matter if you chose the edges E to D or E to H instead as these also had a length of 2. The minimum spanning tree will still have the same length even if a different edge with the same length is selected.
Step 3. Repeat step 2 until all nodes are connected
Examine the connected nodes of A, B and E.
The possible options are shown below in purple.
There are several edges that have a length of 2, which is the shortest route. We can select any of these.
We have chosen to connect B to D as it has a length of 2.
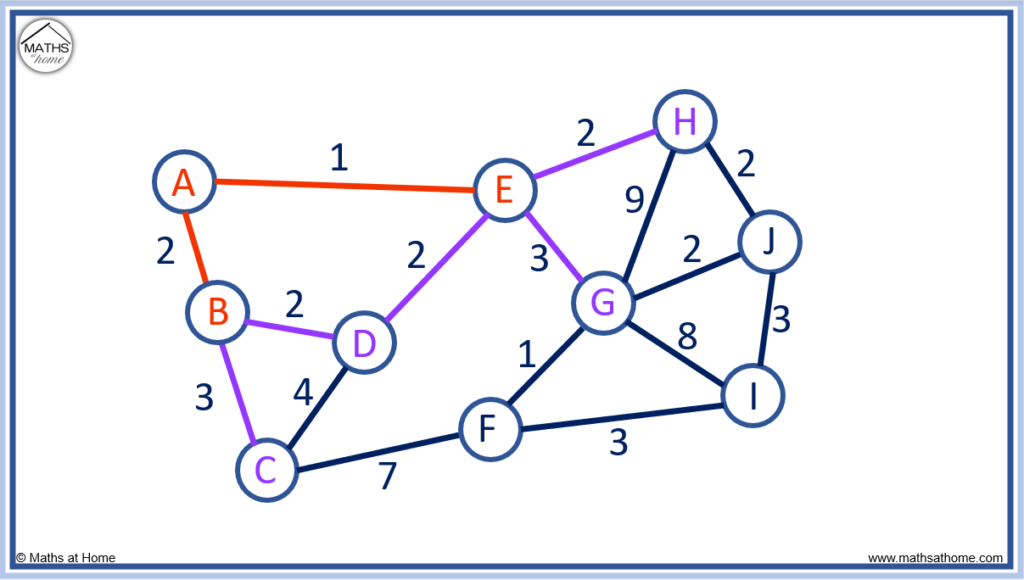
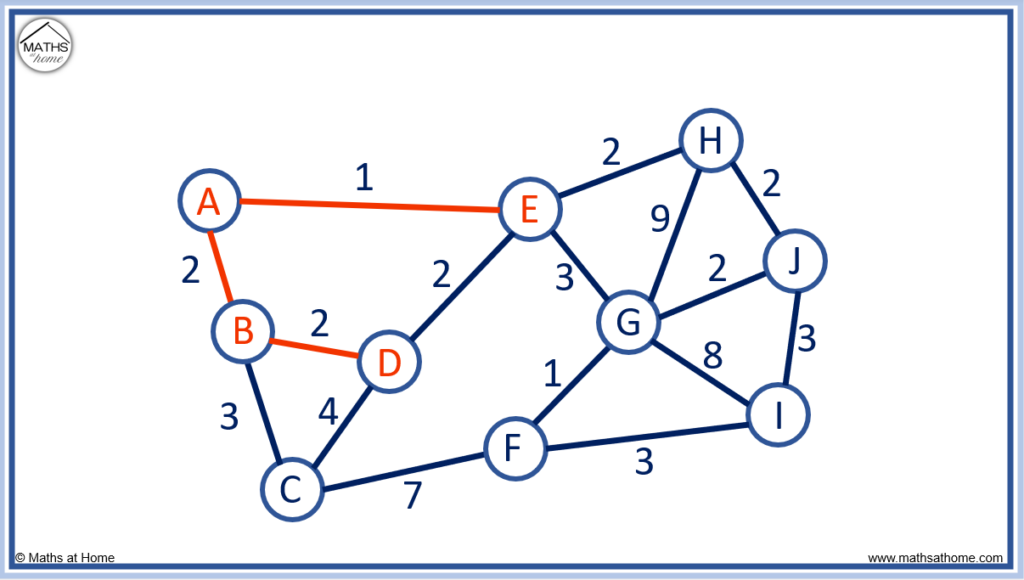
We examine the connected nodes of A, B, D and E and consider how these can be connected to the unconnected nodes.
The possible edges are shown below in purple.
We do not create loops in Prim’s algorithm so we do not connect node D to node E.
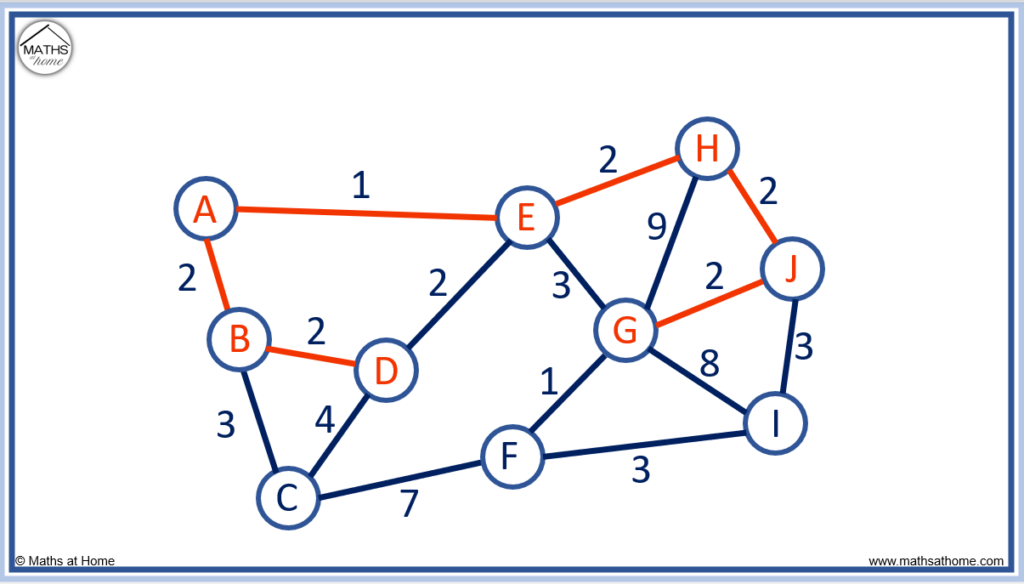
This time, E to H is the only edge that has a length of 2. It is our shortest edge and we must choose to use it.
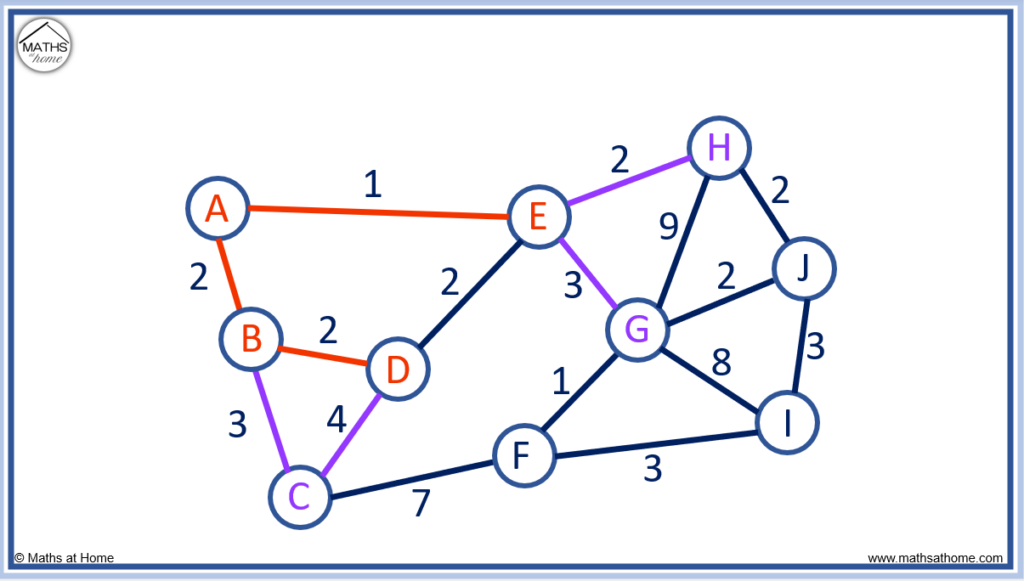
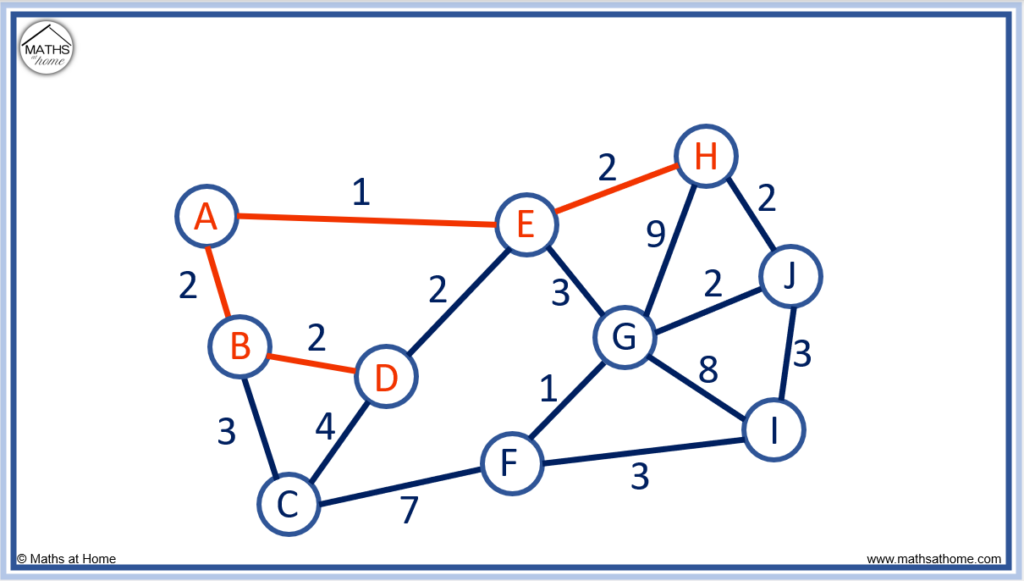
The edges in purple show the options for connecting our unconnected nodes.
This time, we must choose the edge H to J because it has a length of 2. This is the shortest edge length.
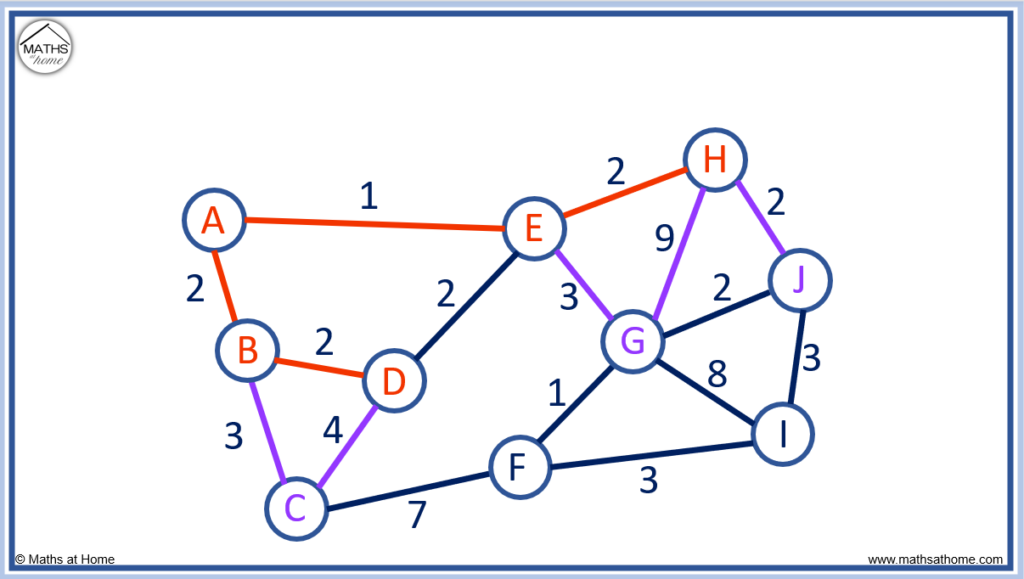
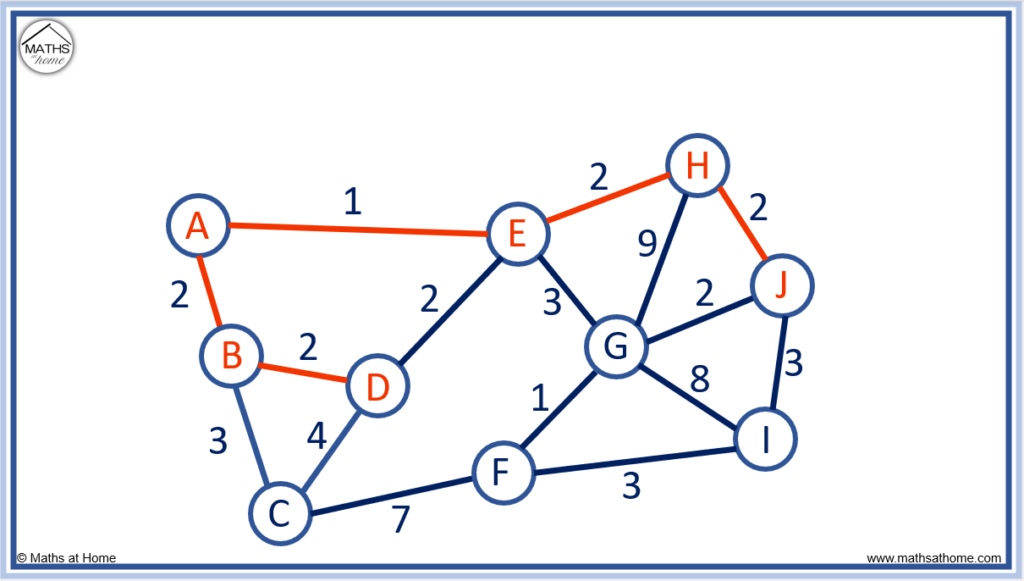
The edges in purple below show the options for connecting the unconnected nodes.
The edge connecting G to J is the shortest edge as it has a length of 2.
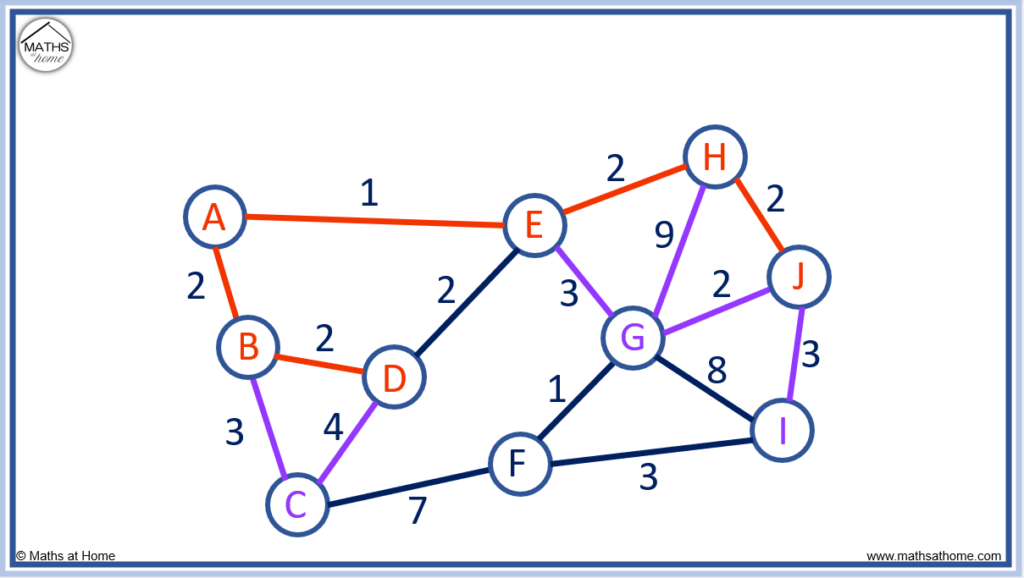
The possible edges to connect the unconnected nodes are now shown below in purple.
This time we must choose the edge connecting G to F. This is because it is the shortest edge with a length of 1.
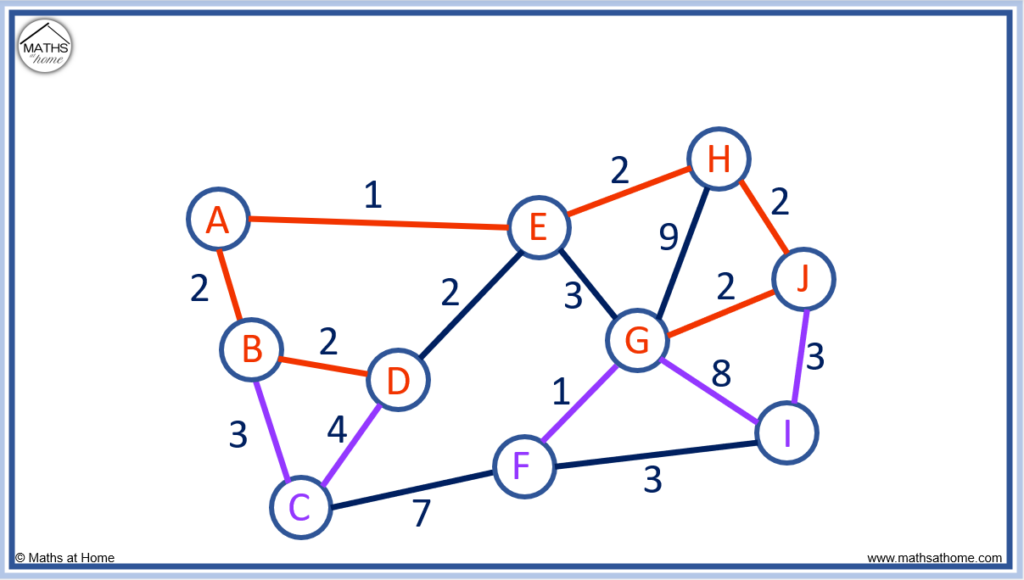
The purple edges below now show us the possible edges that connect the unconnected nodes of C and I.
There is a choice of edges that all have a length of 3. That is B to C, F to I and J to I.
Remember we can choose any of these. We will choose B to C this time.
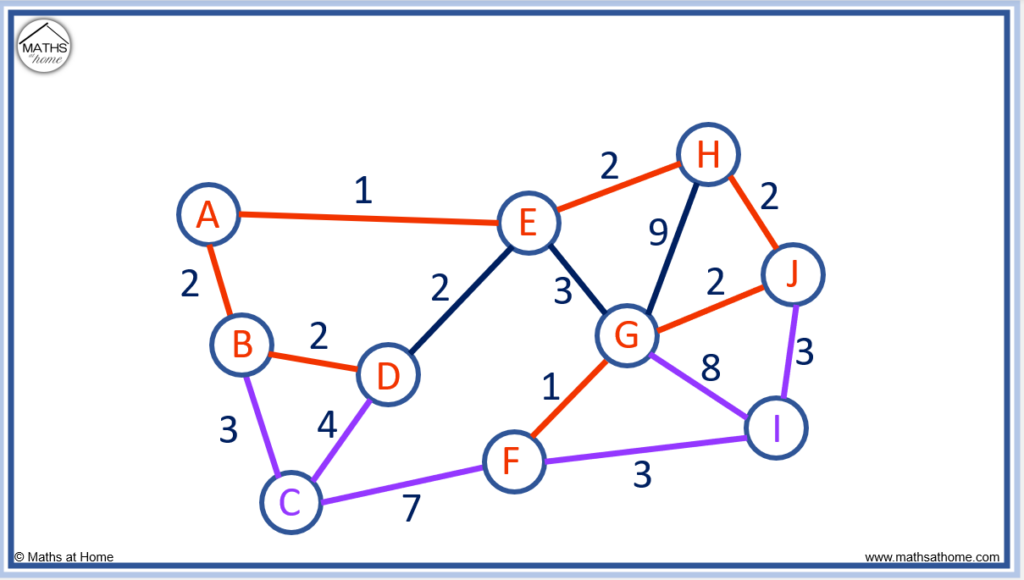
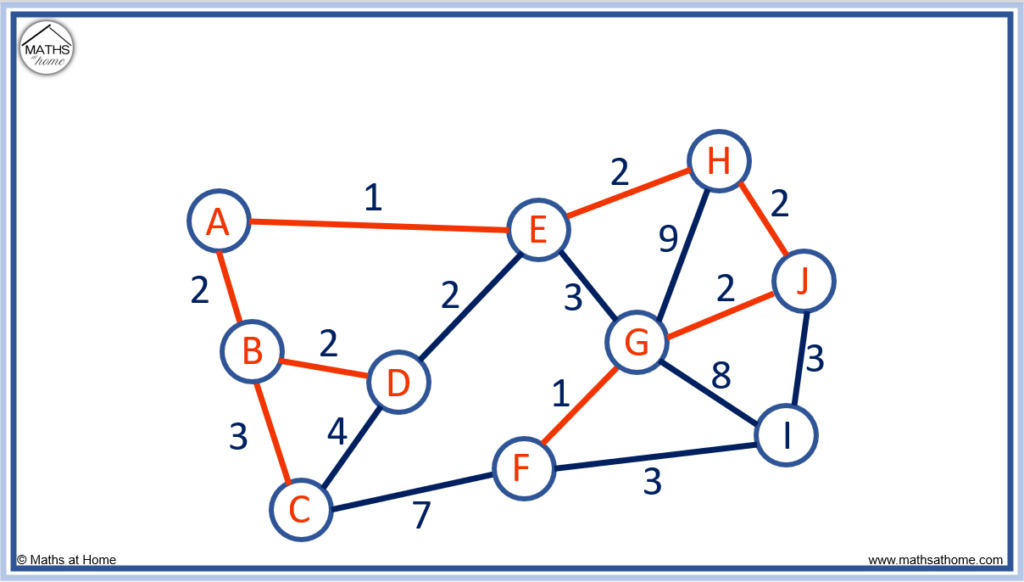
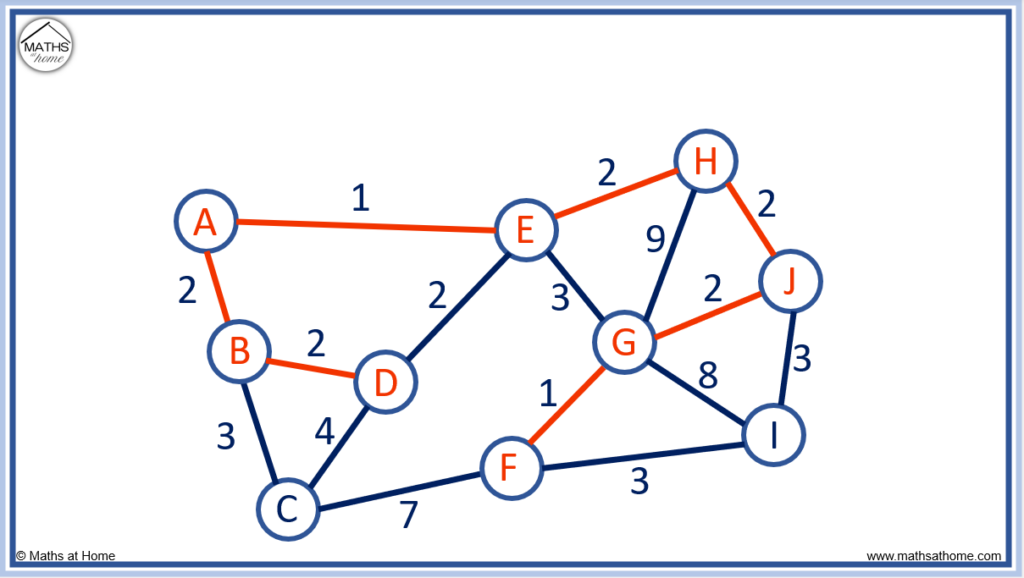
Finally, the only unconnected node is I. The purple edges below show the possible edges to connect the nodes to I.
The shortest edges are F to I and J to I, both with a length of 3.
We can choose either of these edges. We have chosen F to I.
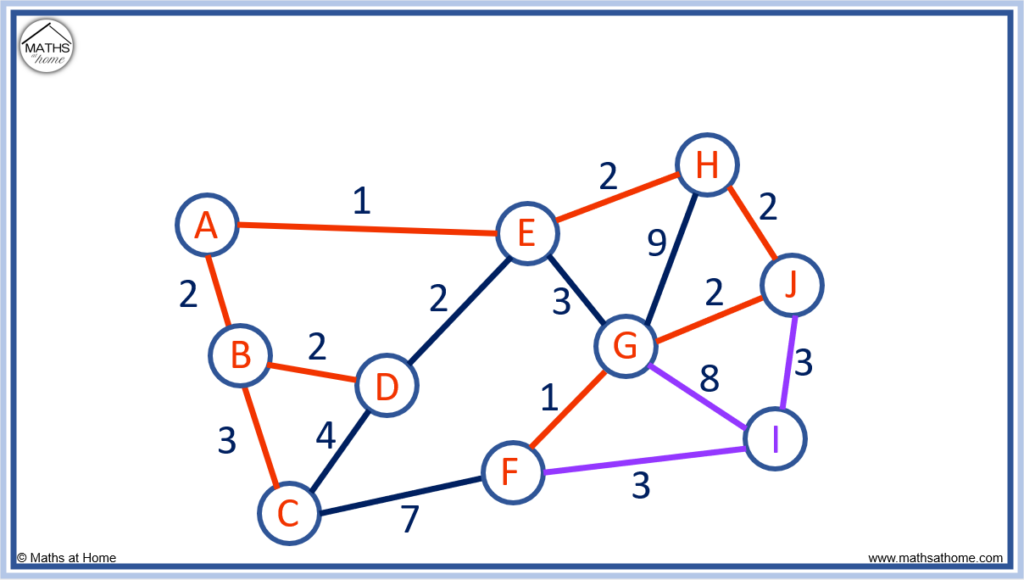
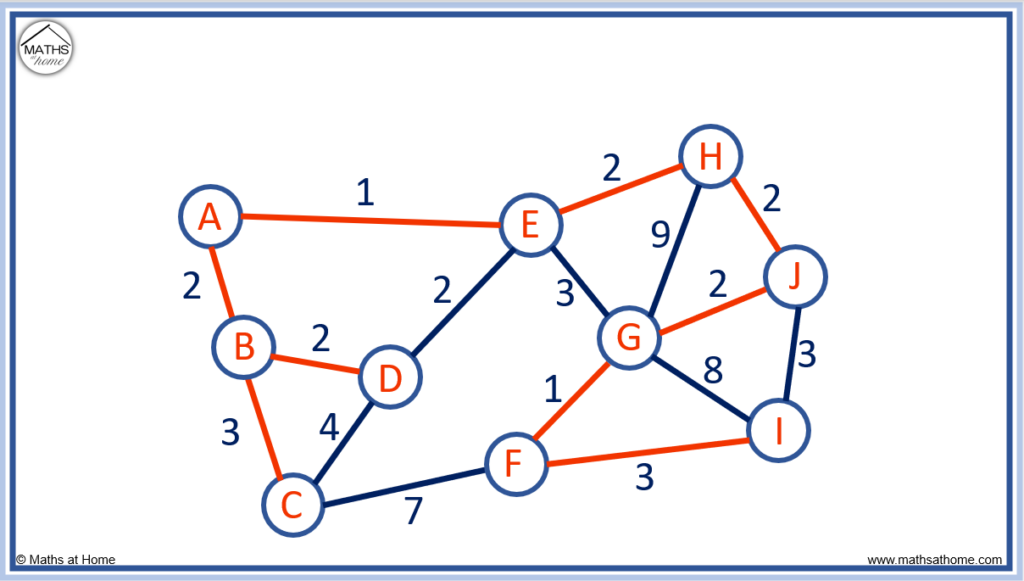
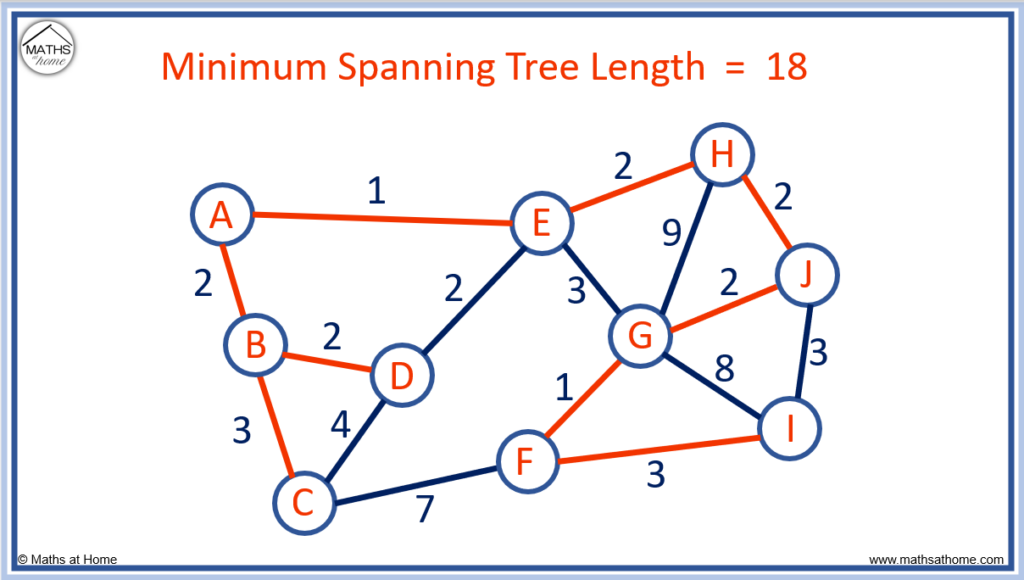
Now all nodes are connected, Prim’s algorithm is complete.
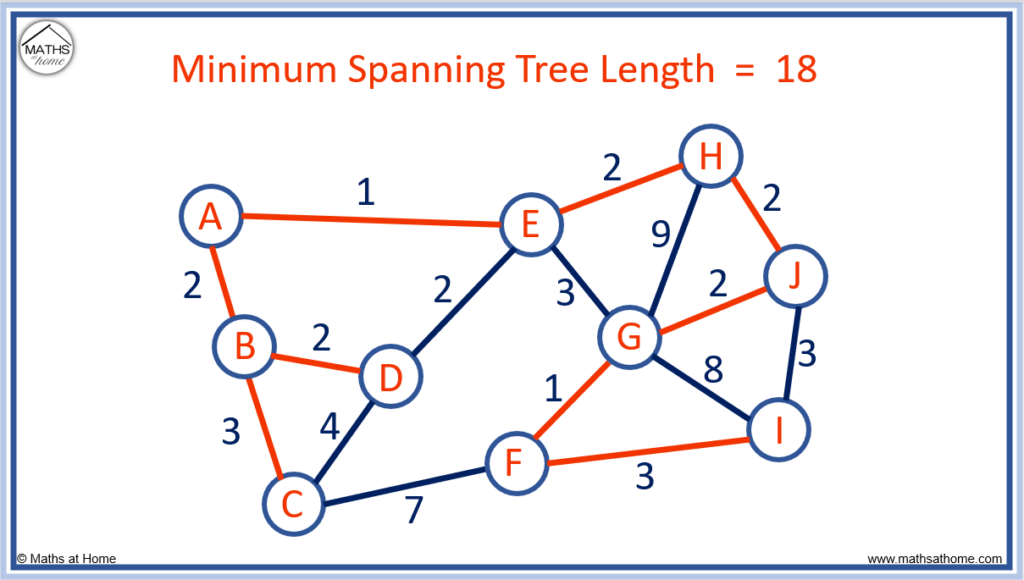
Now we can find the length of the minimum spanning tree by adding up the edge lengths of the spanning tree above.
1 + 2 + 2 + 3 + 2 + 2 + 2 + 1 + 3 = 18 and so, the minimum spanning tree length is 18.
What is a Minimum Spanning Tree?
A minimum spanning tree connects all nodes in a network using the smallest possible sum of the edges. Every node in the network must be connected to another node. This way of connecting all of the nodes gives the smallest answer when the edges are added up.
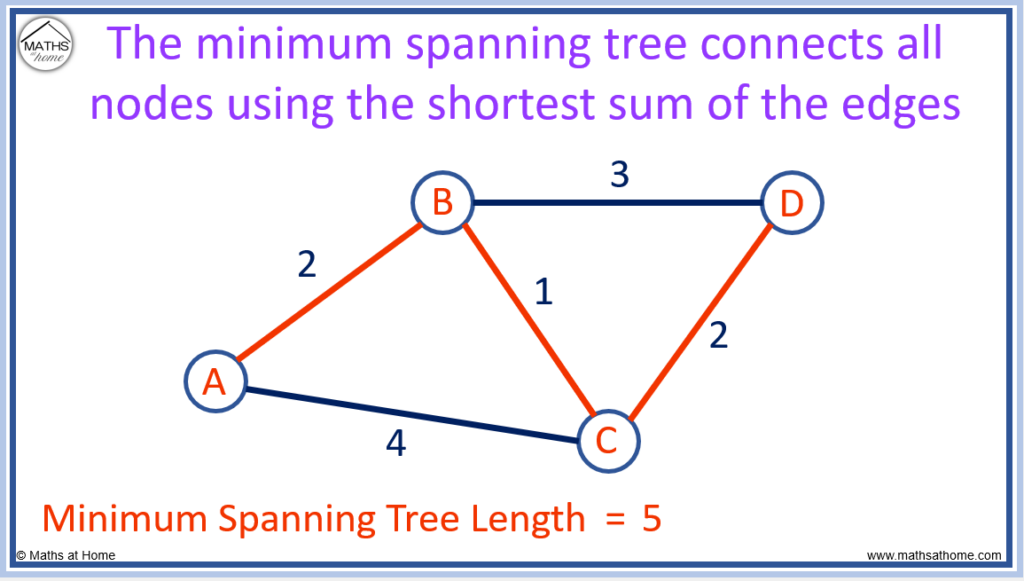
The minimum spanning tree for this graph is shown above.
2 + 1 + 2 = 5. The minimum spanning tree length is 5.
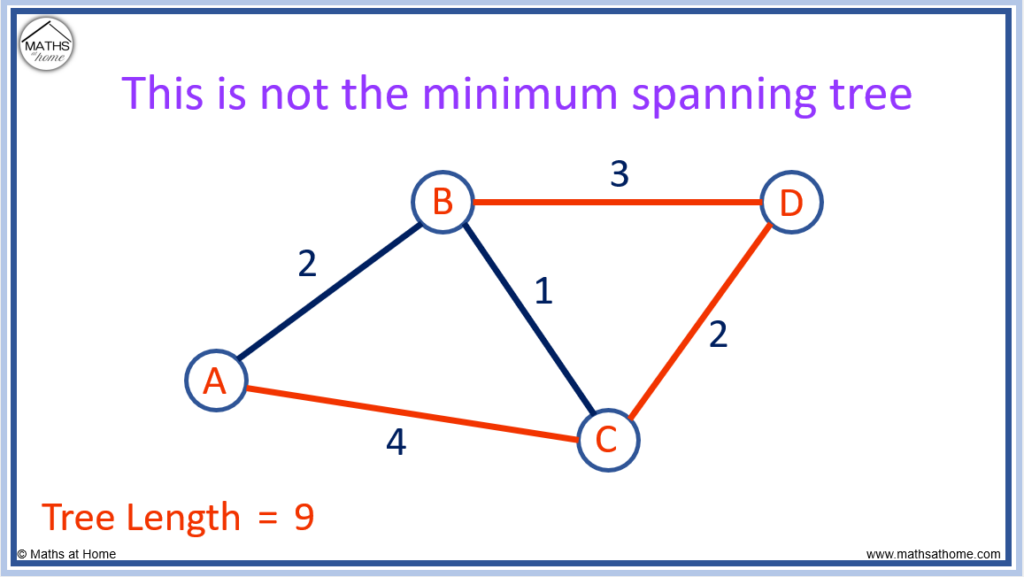
For example, here is another possible way of connecting the nodes that does not result in the minimum spanning tree.
The tree below contains edges of 4, 2 and 3. The tree length is therefore 4 + 2 + 3 = 9.
The minimum spanning tree is 5 and so, this means that there is no possible way to connect all nodes in the network in a shorter manner than 5.
Minimum spanning trees connect all nodes using the least possible total edge lengths. Therefore minimum spanning trees can be used to minimise costs in situations such as connecting transport, plumbing or wiring between different locations.
Real Life Examples of a Minimum Spanning Tree
- For example, A, B, C and D in the network below could represent 4 different towns and the length of each edge could represent the distance in kilometres between them.
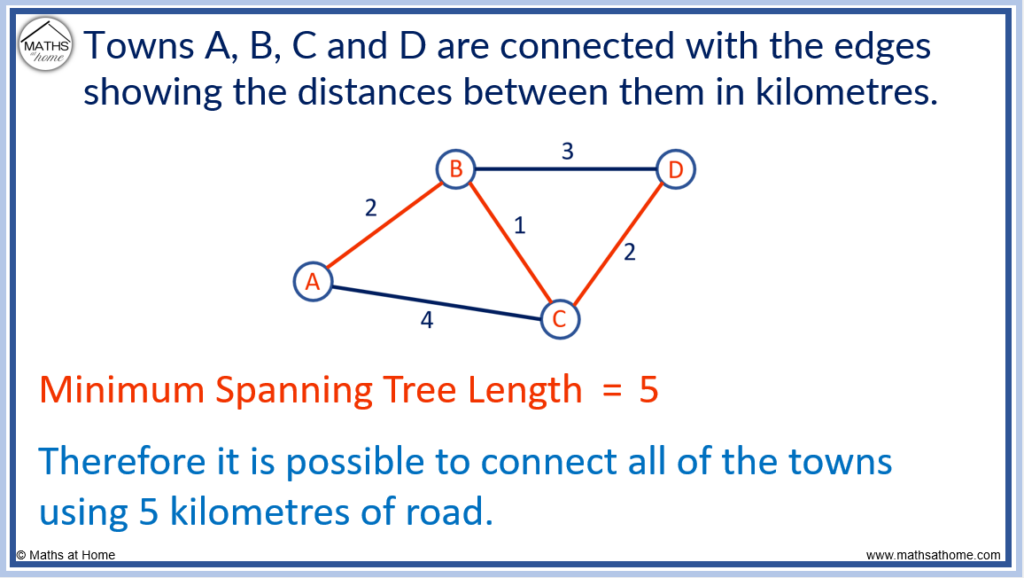
If a delivery driver needed to visit all 4 different towns, the minimum spanning tree below tells us that this could be done by driving the following route ABCD in 5 kilometres. If the driver was not aware of this, he may take a different route which would require more fuel and take more time.
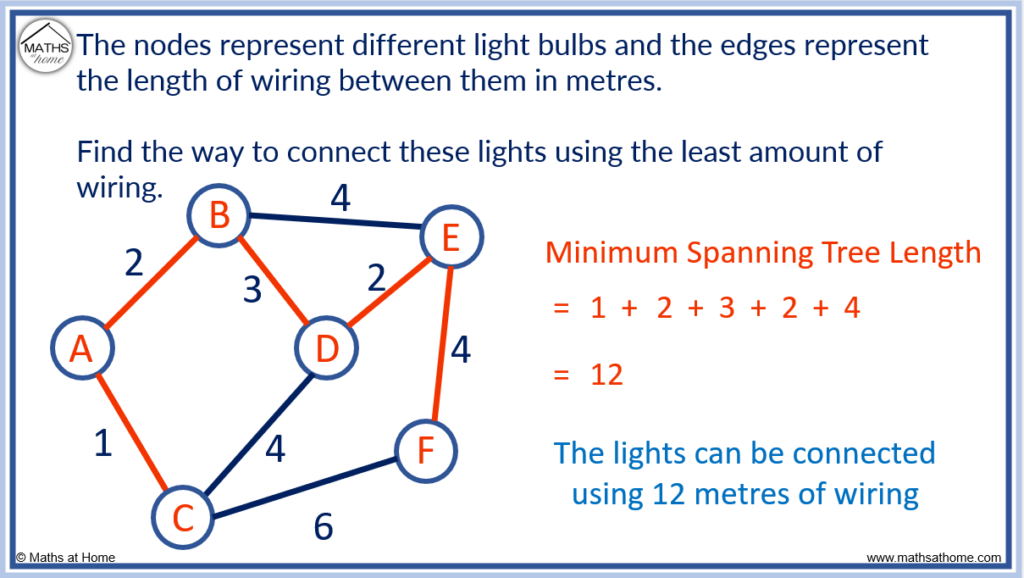
- For example, the nodes below represent different light bulbs and the edges represent the length of wiring used to connect them in metres.
By finding the minimum spanning tree as shown below, the most efficient way to connect the light bulbs is with 12 metres of wiring as shown.
There is no way to connect all of the light bulbs and use less wiring than this.
What is Prim’s Algorithm?
Prim’s algorithm is a greedy algorithm that is used to find the minimum spanning tree for a network. It is used to connect every node together using the smallest possible total obtained when the edges are added together.
For example, Prim’s algorithm has been used on the network below to find the minimum spanning tree.
The minimum spanning tree is 18, which means that there is no other way to connect every node in the network that will produce a total sum of the edges that is less than 18.
Prim’s algorithm is a type of greedy algorithm. A greedy algorithms is a process that is repeatedly evaluated at each stage in order to find an optimal solution.
Prim’s algorithm involves looking at every node every time a new node is connected. Every time a new node is connected, we look for the shortest route that connects to an unconnected node.
Prim’s Algorithm Compared with Kruskal’s Algorithm
Both Prim’s algorithm and Kruskal’s algorithm are used to find the minimum spanning tree. Use Prim’s algorithm when the graph is more complex with lots of edges. Use Kruskal’s algorithm when the graph is simple with not many edges. Kruskal’s algorithm is easier to implement but is less efficient than Prim’s algorithm as the graph gets larger.
To do Kruskal’s algorithm:
- Connect the shortest edge. If there are several, just choose one.
- Connect the next shortest edge available in the same manner.
- Keep connecting the shortest edges available until all nodes are connected but do not choose an edge that completes a circuit.
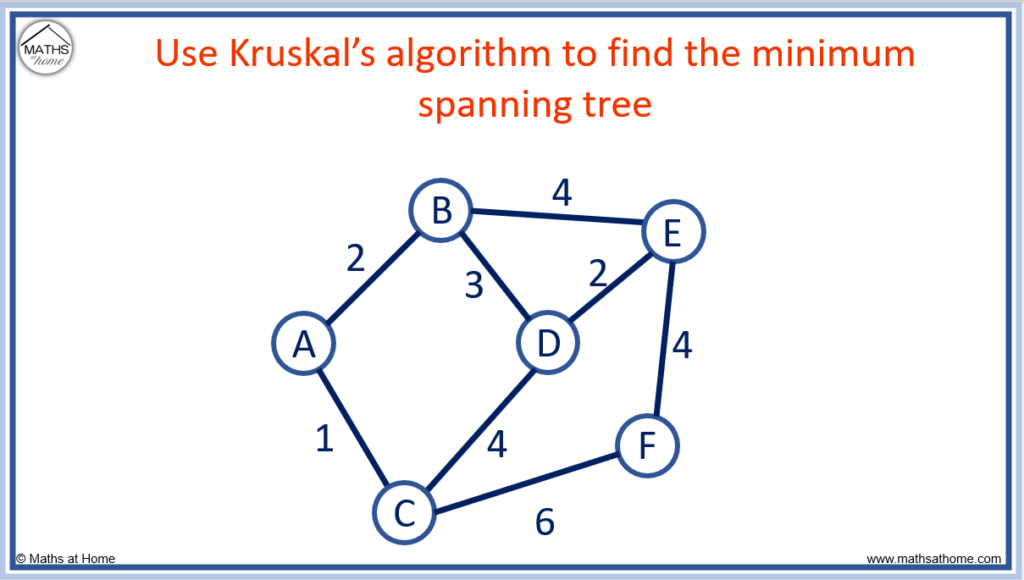
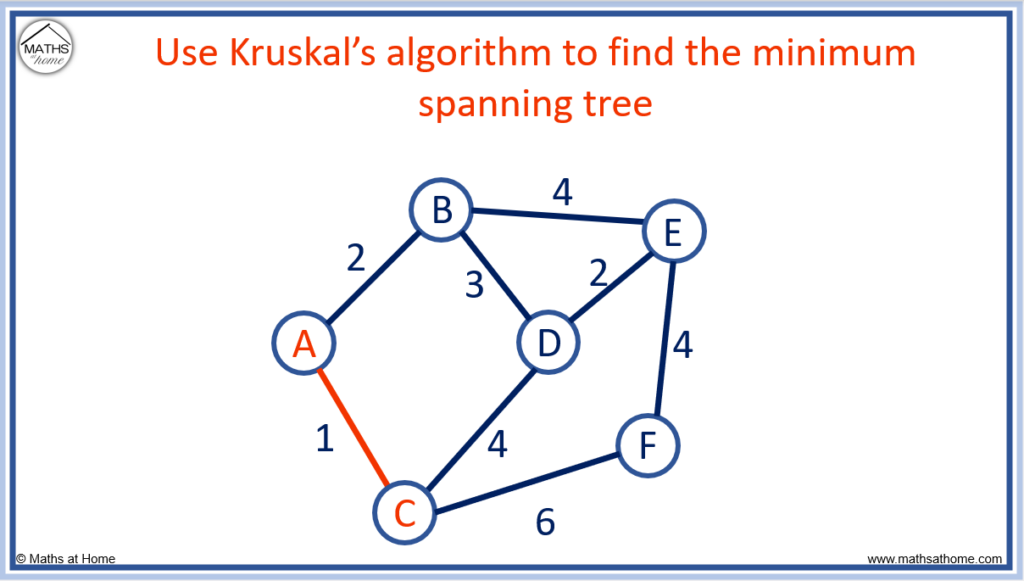
Step 1. Connect the shortest edge
The shortest edge is A to C, which has a length of 1.
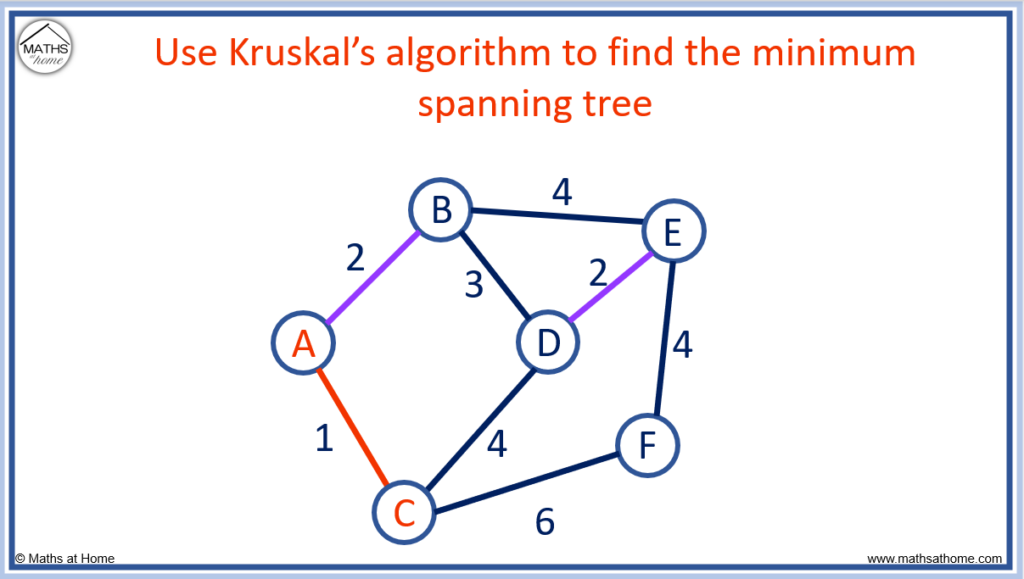
Step 2. Connect the next shortest edge available in the same manner
The next shortest edges available are A to B and D to E, which both have a length of 2.
We choose any of these edges. We will choose the edge A to B.
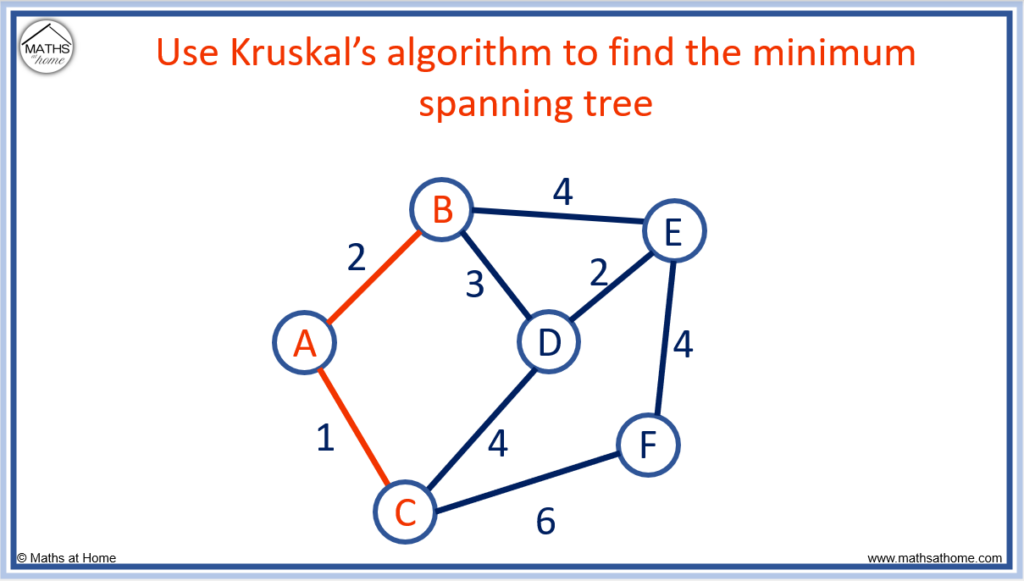
Step 3. Keep connecting the shortest edges available until all nodes are connected but do not choose an edge that completes a circuit
The next shortest edge available is D to E, with a length of 2.
When using Kruskal’s algorithm, it is possible to connect nodes in separate regions. D can be connected to E, even though neither D or E are connected to any other node.
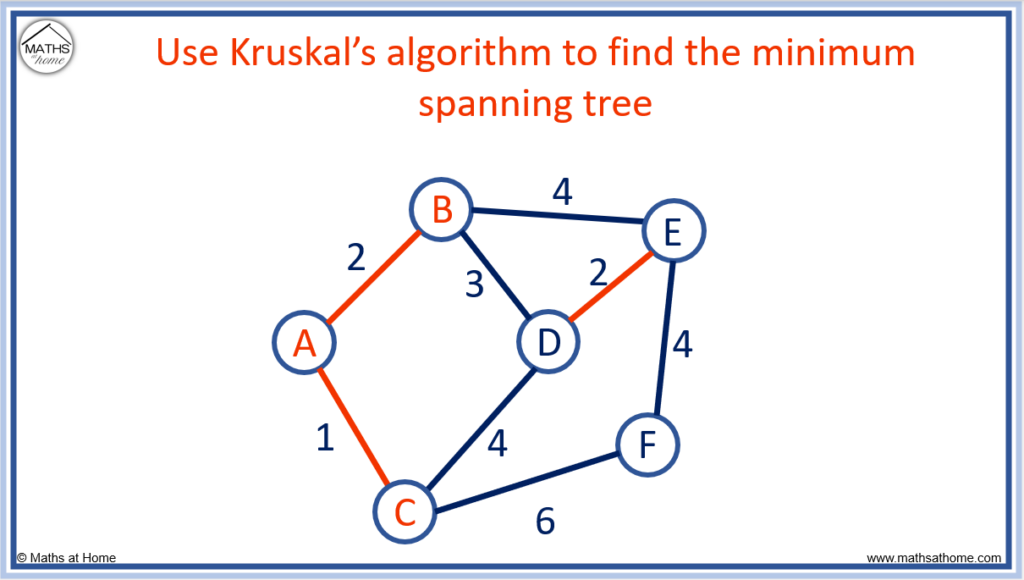
The next shortest edge is B to D, which has a length of 3.
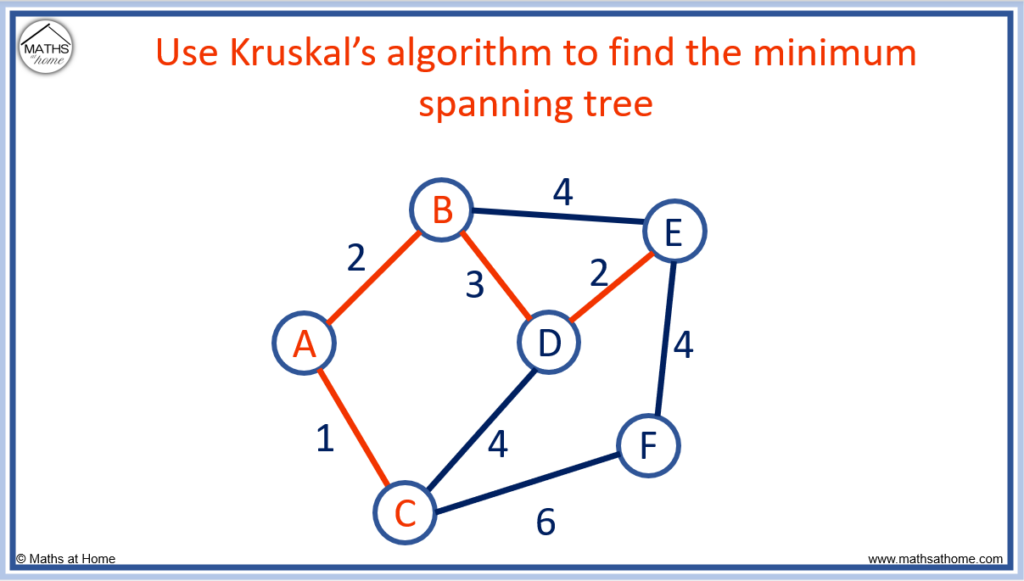
The next shortest edge of E to F has a length of 4.
We cannot choose to connect B to E or C to D because both of these edges would create a loop. We never complete a loop in Kruskal’s algorithm.
We will connect E to F.
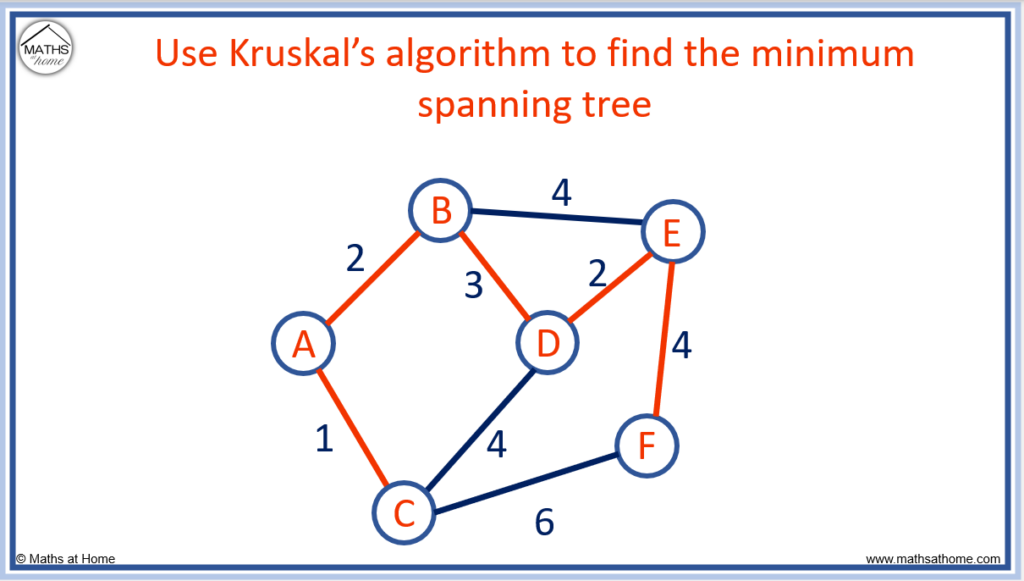
Now all nodes are connected, Kruskal’s algorithm is complete.
The minimum spanning tree is found by adding up the lengths of the connected edges.
1 + 2 + 3 + 2 + 4 = 12 and so, the minimum spanning tree length is 12.
This is the same result as obtained using Prim’s algorithm just using a different method.
