How to Find the Area of a Triangle Using the Sine Rule

Sine Rule for Area: Video Lesson

What is the Sine Rule for Area?

The sine rule for the area of a triangle is Area = ½ ab sinC, where ‘a‘ and ‘b‘ are two sides of a triangle and ‘C‘ is the angle in between them. The sine rule can be used to find the area of any triangle, even if the base and height are not known. At least 2 sides of the triangle and the angle between them must be known.

A r e a. equals one half a. b sine C

The Sine Rule for Area
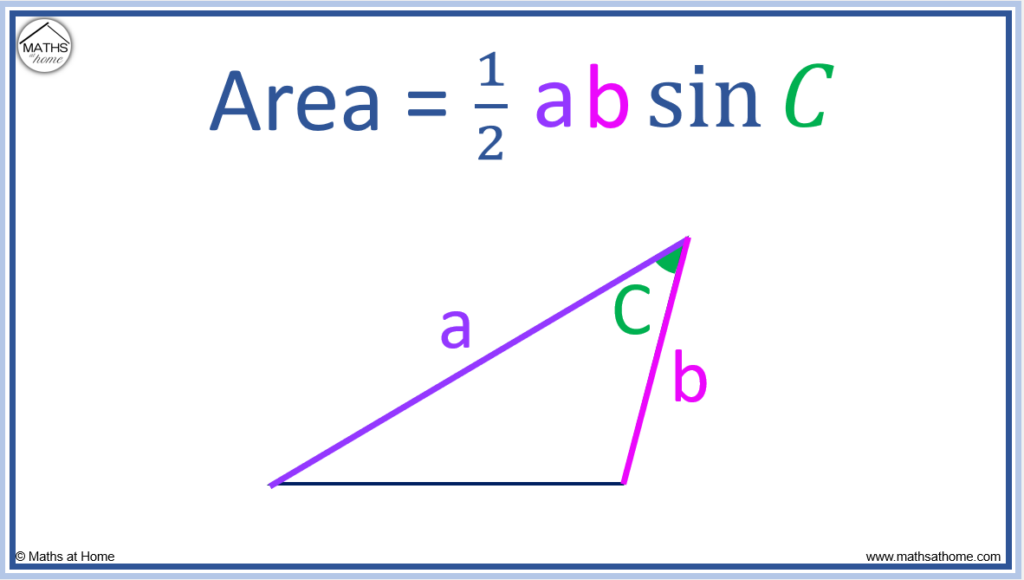
the sine rule for the area of a triangle formula

To use the sine rule for area, 2 side lengths must be known and the angle in between the two sides must be known.

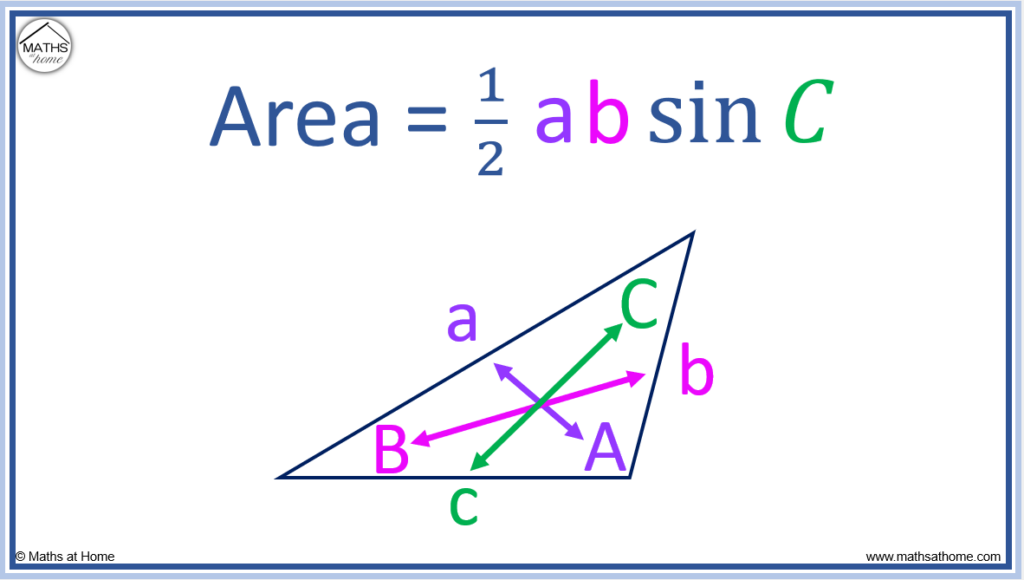
When labelling the sides of a triangle, the lowercase letters: a, b and c are used for the sides. The uppercase letters: A, B and C are used for the angles.

  • Angle A must be opposite the side length a.
  • Angle B must be opposite the side length b.
  • Angle C must be opposite the side length c.

In the sine rule for area, we only need sides ‘a‘, ‘b‘ and the angle ‘C‘ in between them.

labelling the sides and angles of a triangle for using trigonometry sine rule

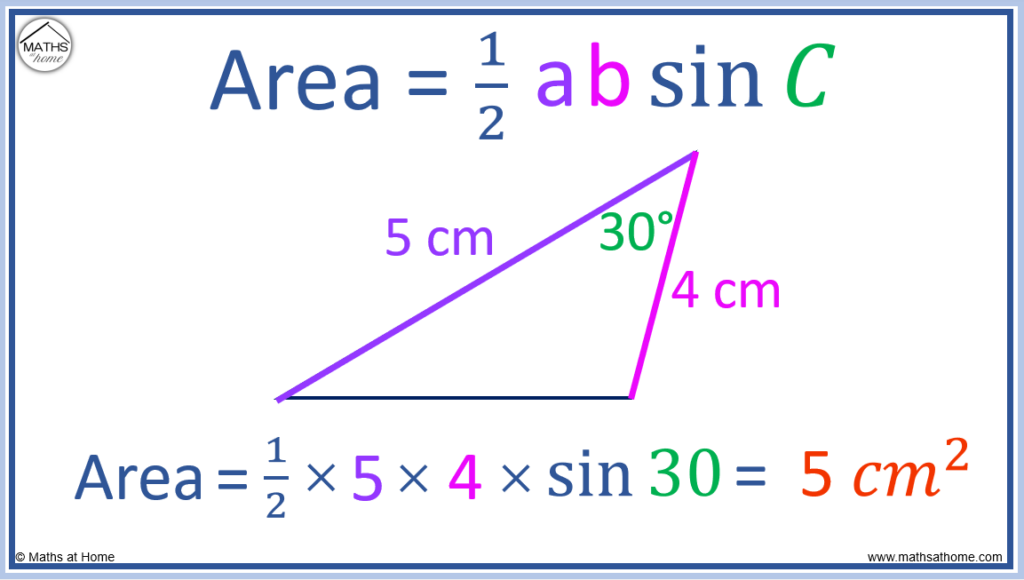
Example 1

Find the area of a triangle with side lengths 5 cm and 4 cm, with enclosed angle of 30°.

  • ‘a’ = 5
  • ‘b’ = 4
  • ‘C’ = 30°

A r e a. equals one half a. b sine C becomes A r e a. equals one half times 5 times 4 times sine 30.

one half times 5 times 4 times sine 30 equals 5 and therefore, the area of the triangle is 5 cm2.

Example of using the sine rule for area of a triangle

Example 2

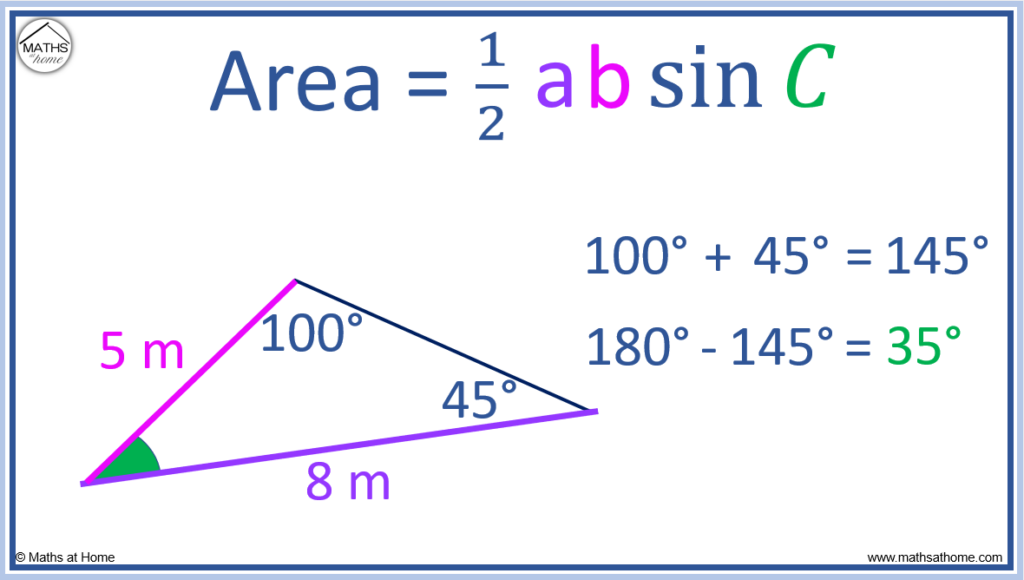
Find the area of a triangle with side lengths 5 m and 8 m.

The enclosed angle between these sides is unknown but the other two angles of the triangle are 100° and 45°.

The enclosed angle between the two known sides must be calculated first.

Angles in a triangle add to 180°.

The two known angles, 100° and 45° sum to 145°.

Therefore the enclosed angle is:

180° – 145° = 35°

finding a missing angle before using the sine rule

Now that the enclosed angle has been calculated, the sine rule can be used to calculate the area of the triangle.

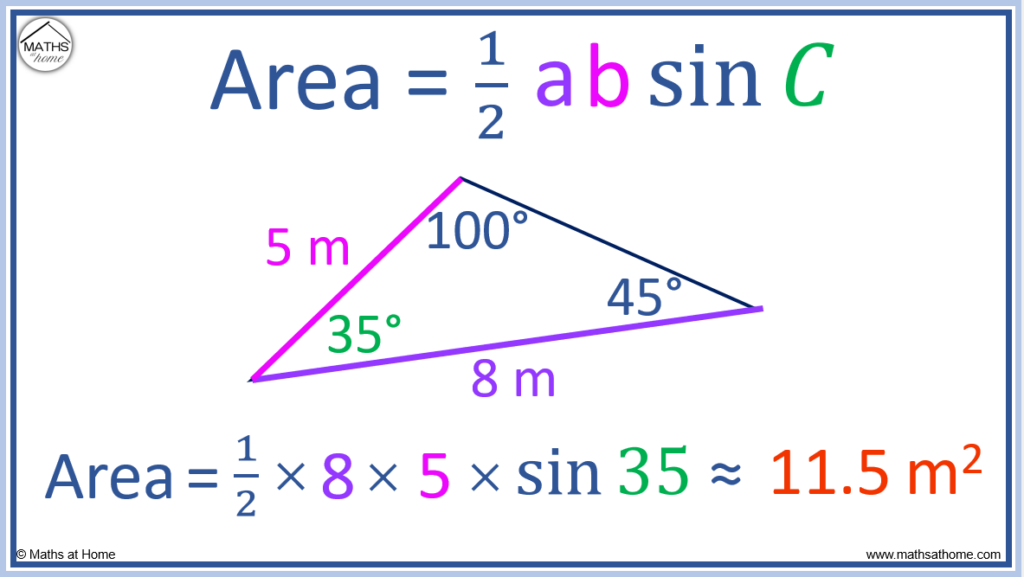
example of calculating the area of a triangle using sine
  • ‘a’ = 8, ‘b’ = 5 and ‘C’ = 35°.
  • A r e a. equals one half a. b sine C becomes one half times 8 times 5 times sine 35
  • A r e a. almost equals 11.5 m squared

The area of the triangle is found to be approximately 11.5 m2.

How to Find the Area of a Triangle Using the Sine Rule

To find the area of a triangle using the sine rule:
  1. Multiply two sides of the triangle together.
  2. Multiply this by the sine of the angle between the sides.
  3. Divide the result by 2.

Example

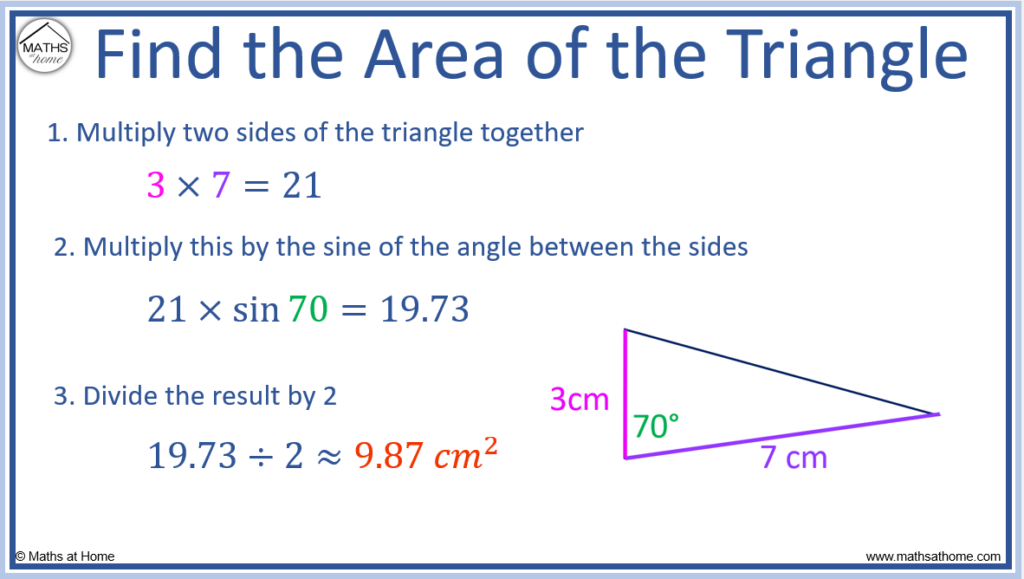
Find the area of the triangle with side lengths 3 cm and 7 cm. The angle between these sides is 70°.

1. Multiply the two sides of the triangle together

The two sides have lengths 3 cm and 7 cm. Multiplying these sides, 3 × 7 = 21.

2. Multiply this by the sine of the angle between the sides

The angle between the sides is 70°.

21 times sine 70 almost equals 19.73.

3. Divide the result by 2

19.73 divided by 2 almost equals 9.87 and since the sides are measured in cm, the area of the triangle is approximately 9.87 cm2.

the sine rule for area of a triangle in steps

Sine Rule for Area Calculator

The sine rule area calculator is used to calculate the area of a triangle given any two sides of the triangle and an enclosed angle between them.

Side length ‘a’ is simply any side of the triangle.

Side length ‘b’ is any other side of the triangle.

Angle ‘C’ must be the angle in between these two sides.

Sine Rule for Area Proof

The sine rule for the area of a triangle can be derived using right-angled trigonometry. For a triangle with base ‘b‘ and an angle ‘C’ between the base and side ‘a‘, the perpendicular height is equal to ‘a sinC’. The area of a triangle is given by Area = ½×base×height. Substituting for height, the sine rule is obtained as Area = ½ ab sinC.

The proof of the sine rule can be shown more clearly using the following steps.

1. Consider a triangle with sides ‘a’ and ‘b’ with enclosed angle ‘C’.

The base of this triangle is side length ‘b’.

2. Consider the right-angled triangle formed from the height.

Using right-angled trigonometry, the height is equal to a. times sine C or a. sine C.

This is because the height is the opposite side to angle C and ‘a’ is the hypotenuse.

From trigonometry, .O equals H times sine theta.

Substituting O equals h of e i g of h of t, H equals a. and theta equals C, we obtain h of e i g of h of t equals a. sine C.

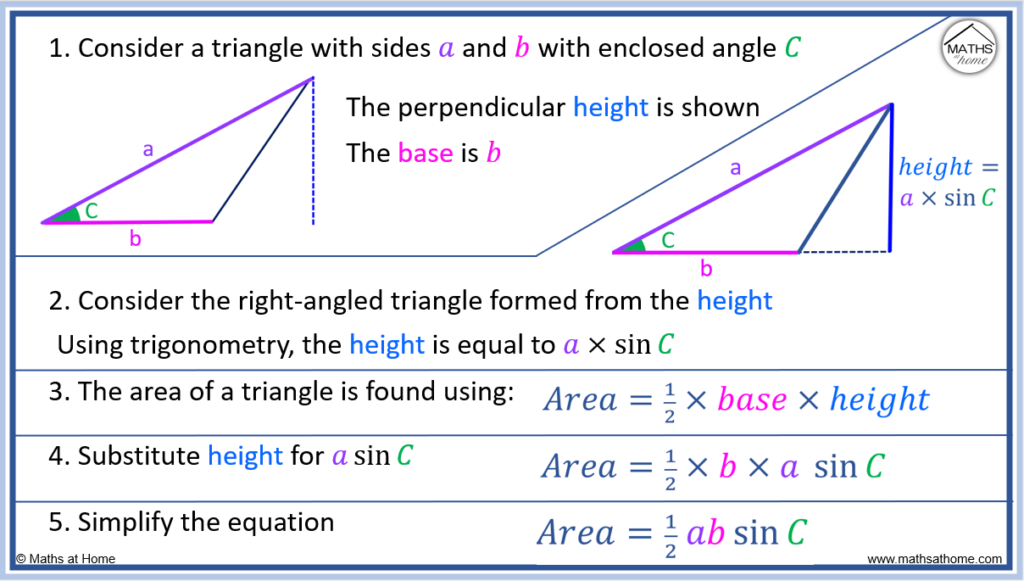
proof of the sine rule for area of a triangle

3. The area of a triangle is found using A r e a. equals one half times b a. s e times h of e i g of h of t

4. Substitute height for a. sine C

The base is equal to ‘b’ and the height is equal to ‘a sinC‘.

A r e a. equals one half times b a. s e times h of e i g of h of t becomes A r e a. equals one half times b times a. sine C

5. Simplify the equation

A r e a. equals one half times b times a. sine C simplifies to the sine rule for area as we know it: A r e a. equals one half a. b sine C.

The sine rule for area works for any triangle, including non-right-angled triangles.

Finding the Area of a Triangle Using the Sine and Cosine Laws

To use the sine rule to find the area of a triangle, we must know two sides and the angle between them. Alternatively, if three sides are known the cosine rule can be used to find an angle first. If two sides and a non-enclosed angle are known, use the sine rule to find the enclosed angle.

In mathematics, the sine rule for the area of a triangle is A r e a. equals one half a. b sine C.

This should not be confused with the general sine rule: S i n A over a. equals S i n B over b which is used to calculate missing sides or angles rather than find the area of a triangle.

Example Involving the Sine Rule

In the example below, two sides are known as 4m and 8 m long.

The angle opposite the 8 m long side is 100°.

The sine rule can be used to find the angle C in the diagram below.

Writing the sine rule as sine C over c equals sine A over a., this can be rearranged to sine C equals c sine A over a..

Substituting the values of A = 100°, ‘c’ = 4 and ‘a’ = 8, sine C equals 4 sine 100 over 8.

Evaluating this, sine C almost equals 0.492 and so, C almost equals the inverse sine of 0.492 and therefore the angle is C almost equals 29.5 degrees.

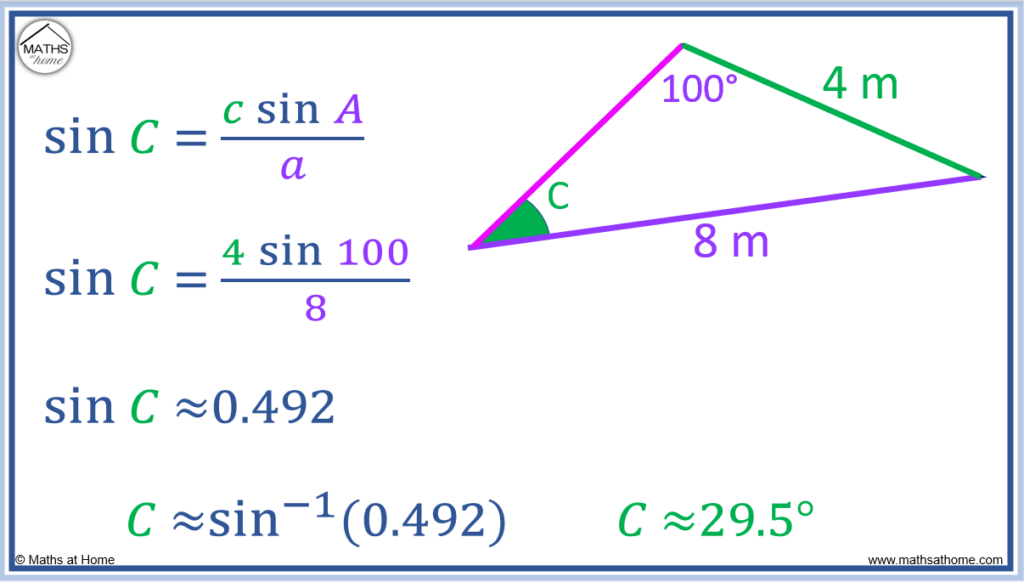
sine rule to find a missing angle
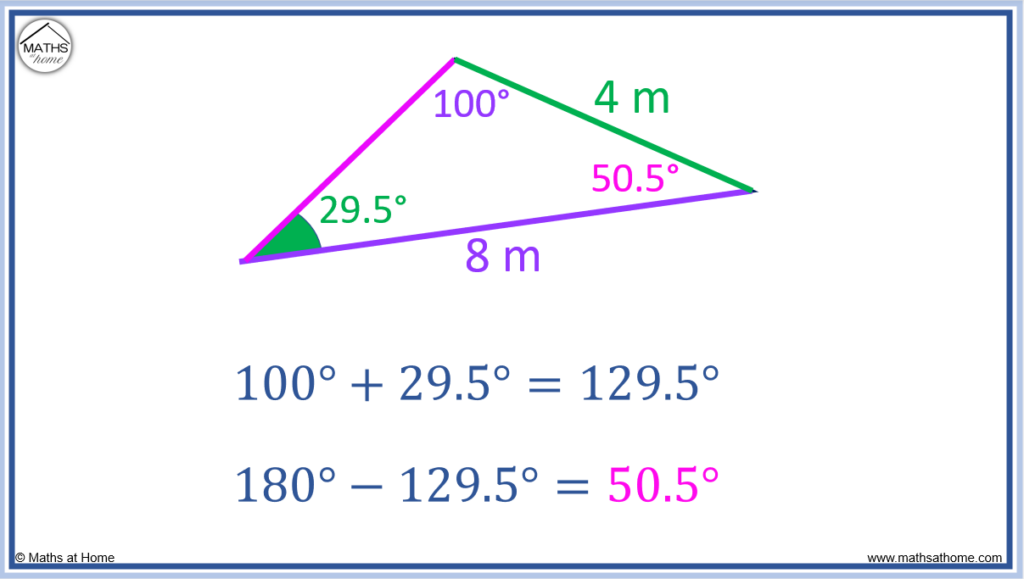
using the sum of interior angles to find a missing angle in a triangle

This angle is not enclosed by two known sides and so, the sine rule cannot be used just yet.

The third angle of the triangle must be found using the fact that angles in a triangle always sum to 180°.

180° – 100° – 29.5° = 50.5°. Therefore the missing third angle of the triangle is 50.5°.

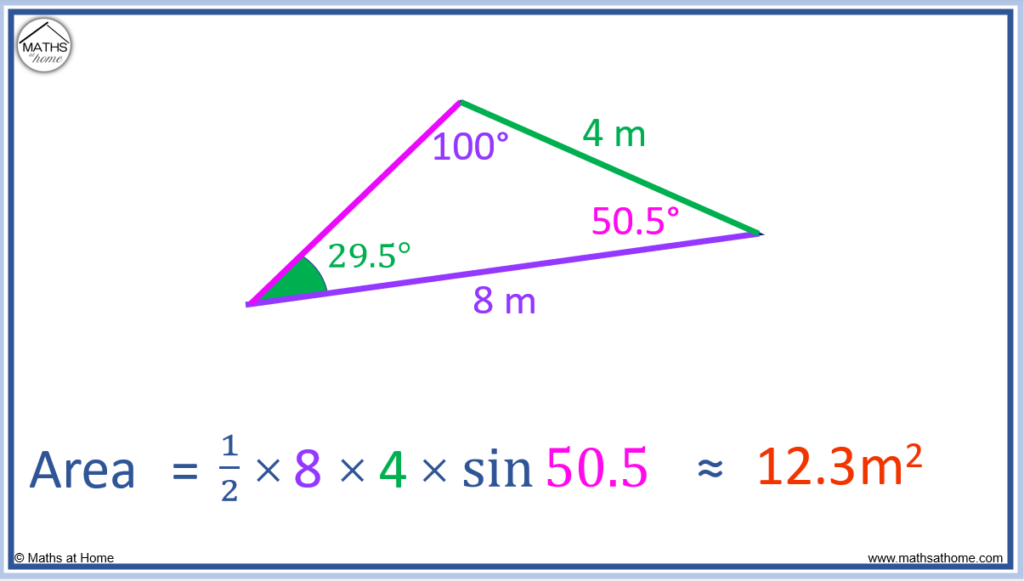
sine rule for area

The sine rule for the area of a triangle can now be used.

‘a’ and ‘b’ are two known sides that encompass a known angle.

Therefore ‘a’ = 8, ‘b’ = 4 and C = 50.5°.

A r e a. equals one half a. b sine C becomes A r e a. equals one half 8 times 4 times sine 50.5.

Evaluating this, A r e a. almost equals 12.3 m squared.

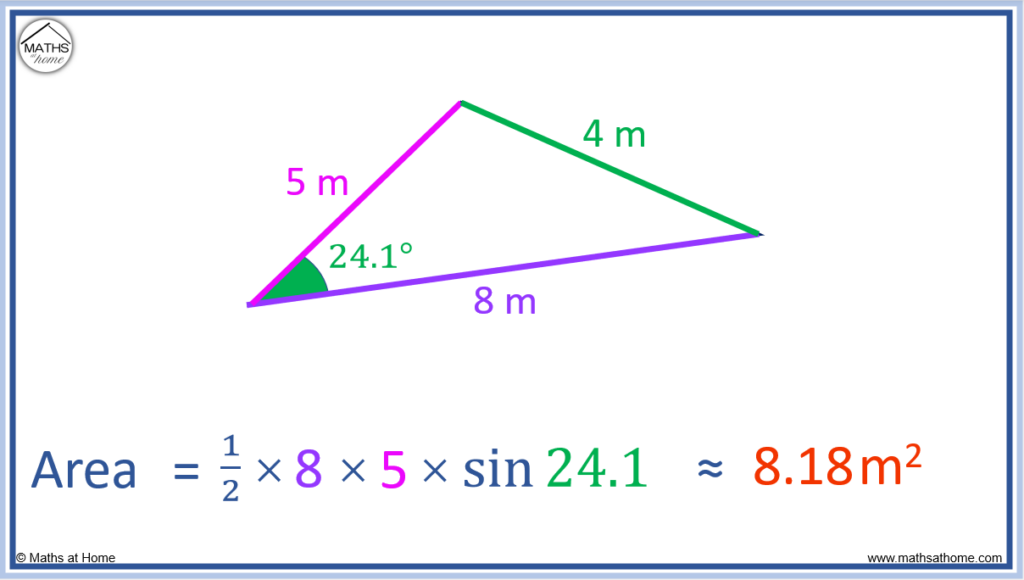
Example Involving the Cosine Rule

In this example, all three side lengths are known as 5 m, 4m and 8m.

We need to know one of the angles between two of the sides. This has been labelled C in the diagram below.

Since this angle is C, the side opposite this must be labelled ‘c’. Therefore ‘c’ = 4.

‘a’ = 5 and ‘b’ = 8. It does not matter which way around these are labelled.

The cosine rule, c squared equals a. squared plus b squared minus 2 a. b cosine C can be rearranged for the angle C as C equals the inverse cosine of open paren the fraction with numerator a. squared plus b squared minus c squared and denominator 2 a. b close paren.

Substituting the values of ‘a’, ‘b’ and ‘c‘, this becomes: C equals the inverse cosine of open paren the fraction with numerator 8 squared plus 5 squared minus 4 squared and denominator 2 times 8 times 5 close paren.

Evaluating this angle, C almost equals 24.1 degrees.

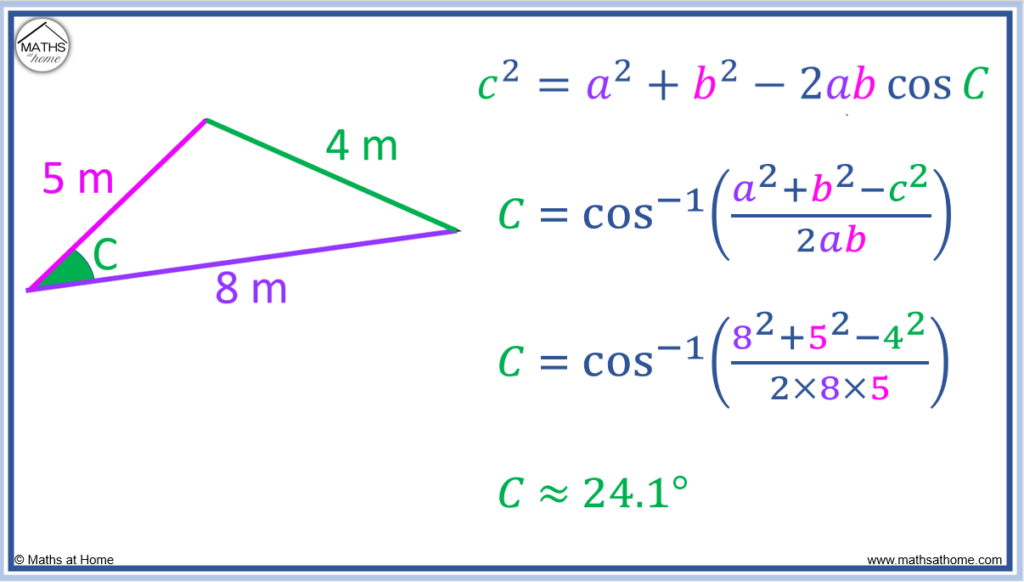
cosine rule to find a missing angle

Now that an angle is known in between the two sides of length 5 m and 8 m, the sine rule for area can be used.

C = 24.1°, ‘a’ = 5 and ‘b’ = 8.

A r e a. equals one half a. b sine C becomes A r e a. equals one half 5 times 8 times sine 24.1.

Evaluating this, A r e a. almost equals 8.18 m squared.

using the sine rule after the cosine rule