Midpoint Between Two Points Video Lesson:
What is the Midpoint?
The midpoint of a line segment is the point that divides the line segment in two. The midpoint is located equally far from each end point. It can be calculated by finding the average of the coordinates of the end points. Add the 𝑥 and y coordinates of the two end points and divide them by two.
A line segment is a portion of a line that has two end points. Unlike a line, a line segment has a fixed length and does not continue on for ever.
The midpoint is found in the middle of a line segment.
If a line segment has two end points at (1, 1) and (9, 7), the midpoint of the line segment is found at (5, 4).
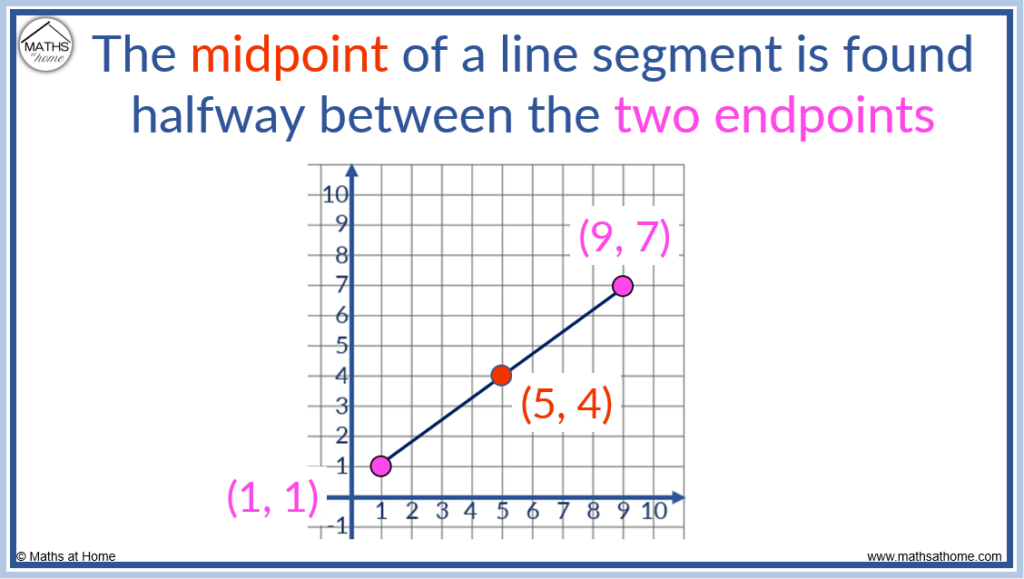
The midpoint is always equally far from each end point.
The midpoint (5, 4) is 4 right and 3 up from the end point of (1, 1). It it is 4 left and 3 down from the other end point of (9, 7).
The midpoint is the average of the two end point coordinates.
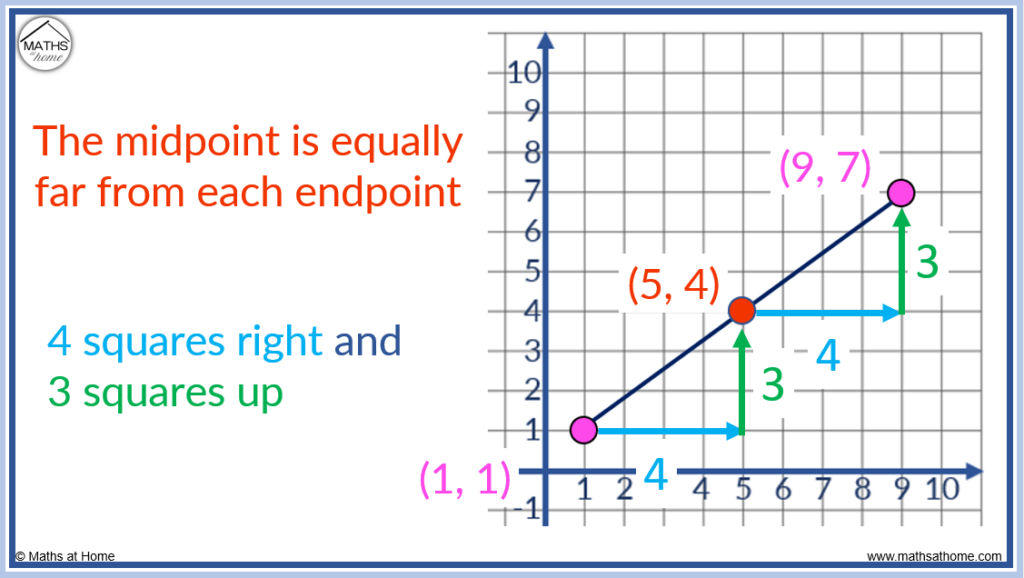
The midpoint divides the line segment in the ratio 1:1. This means that the length of the line segment is the same on each side of the midpoint.
How to Find the Midpoint Between 2 Points
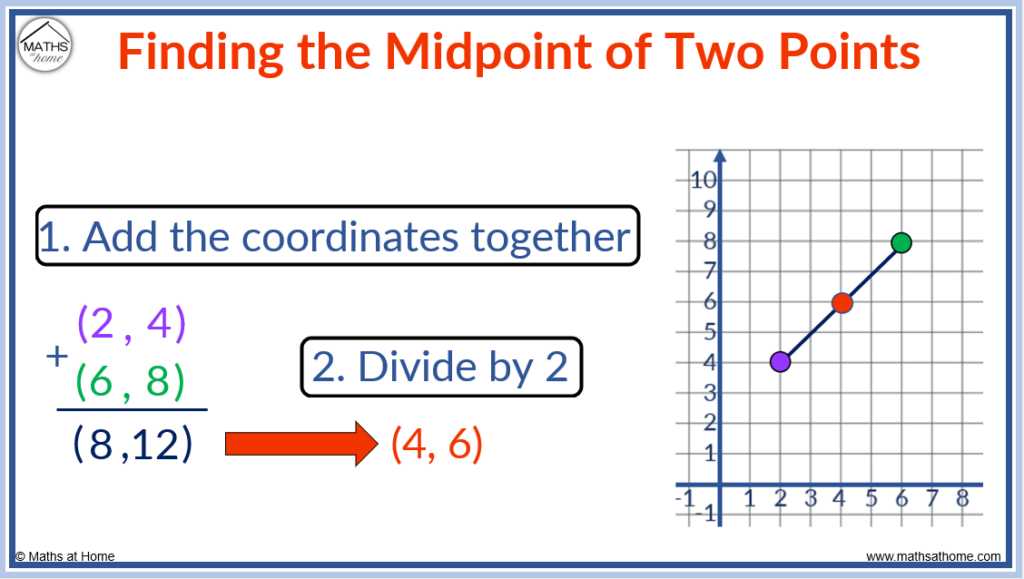
To find the midpoint between 2 points, add the x-coordinates of the points and the y-coordinates of the points separately and then divide the result by 2. For example, the midpoint of the points (2, 4) and (6, 8) is found by adding the coordinates to get (8, 12) and then dividing by 2 to get (4, 6).
- Add the coordinates
The 𝑥-coordinates are the first numbers written in each pair of coordinates.
In (2, 4) the 𝑥-coordinate is 2 and in (6, 8) the 𝑥-coordinate is 6.
Adding these 𝑥-coordinates, 2 + 6 = 8
The y-coordinates are the second numbers written in each pair of coordinates.
In (2, 4) the y-coordinate is 4 and in (6, 8) the y-coordinate is 8.
Adding these y-coordinates, 4 + 8 = 12
Adding the coordinates of (2, 4) and (6, 8), we obtain (8, 12).
2. Divide by 2
Dividing both numbers in (8, 12) by 2, we obtain (4, 6).
The midpoint of (2, 4) and (6, 8) is therefore (4, 6).
Examples of Finding the Midpoint of 2 Points
| Point 1 | Point 2 | Sum of Coordinates | Midpoint |
| (3, 1) | (9, 7) | (12, 8) | (6, 4) |
| (10, 3) | (4, 7) | (14, 10) | (7, 5) |
| (4, 4) | (0, 0) | (4, 4) | (2, 2) |
| (5, 1) | (2, 3) | (7, 4) | (3.5, 2) |
| (-6, -2) | (8, 10) | (2, 8) | (1, 4) |
| (-2, 3) | (-12, -2) | (-14, 1) | (-7, 0.5) |
Midpoint of a Line Segment Formula
The formula to calculate the midpoint of a line segment is (𝑥m, ym) = ( (𝑥1+𝑥2)/2, (y1+y2)/2 ), where (𝑥1, y1) and (𝑥2, y2) are the coordinates of each end point. The formula for the midpoint is used to calculate an average of the end points.
The formula for the midpoint of a line segment
are the coordinates of the midpoint
are the coordinates of the first end point
are the coordinates of the second end point

Example
Use the midpoint formula to find the midpoint of (-1, 4) and (7, 2).
The midpoint formula is .
Substituting in the above values, .
Evaluating each calculation, and so, the midpoint is found at
.
(3, 3) is the midpoint of (-1, 4) and (7, 2).

Midpoint of a Line Segment Calculator
How to Find the Midpoint of a Line Segment in Steps
The steps to find the midpoint of a line segment are:- Add the x-coordinates of the two end points. Divide this by 2 to find the x-coordinate of the midpoint.
- Add the y-coordinates of the two end points. Divide this by 2 to find the y-coordinate of the midpoint.
For example, find the midpoint of the line segment between (3, 10) and (1, 12).
1. Add the x-coordinates of the two end points
The x-coordinates are 3 and 1.
3 + 1 = 4
2. Divide this by 2 to find the x-coordinate of the midpoint
4 ÷ 2 = 2 and so, the x-coordinate of the midpoint is 2.
3. Add the y-coordinates of the two end points
The y-coordinates are 10 and 12.
10 + 12 = 22
4. Divide this by 2 to find the y-coordinate of the midpoint
22 ÷ 2 = 11 and so, the y-coordinate of the midpoint is 11.
Therefore the midpoint of (3, 10) and (1, 12) is (2, 11).
Midpoint of a Horizontal Line Segment
The midpoint of a horizontal line segment will have the same y-coordinate as any other point on the line segment. The x-coordinate will be half way in between the x-coordinates at each end of the line segment. Simply divide the length of the line segment by 2 and count this distance from either of the end points.
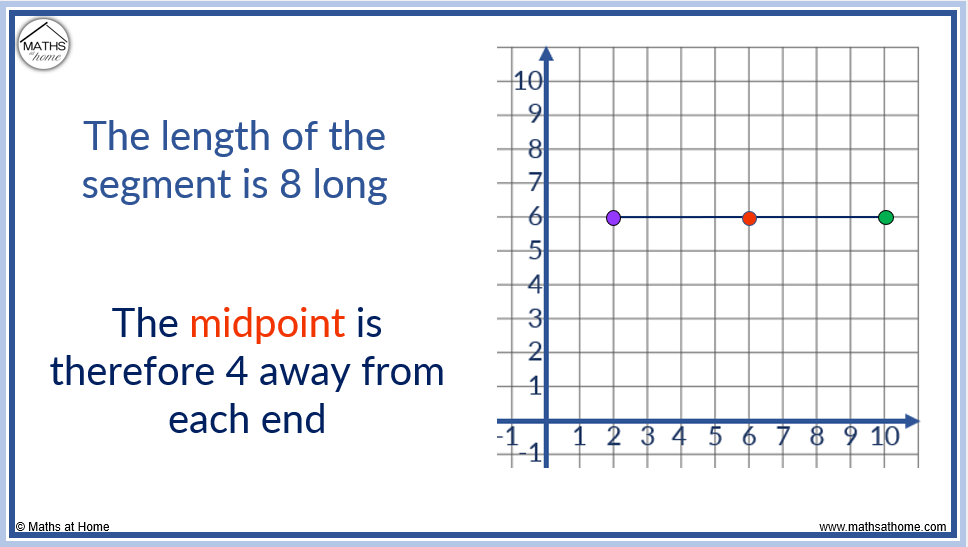
For example, the line segment from (2, 6) to (10, 6) is 8 long.
Therefore the midpoint is found 4 places in from either end point.
The midpoint is at (6, 6). This has the same y-coordinate as each end point.
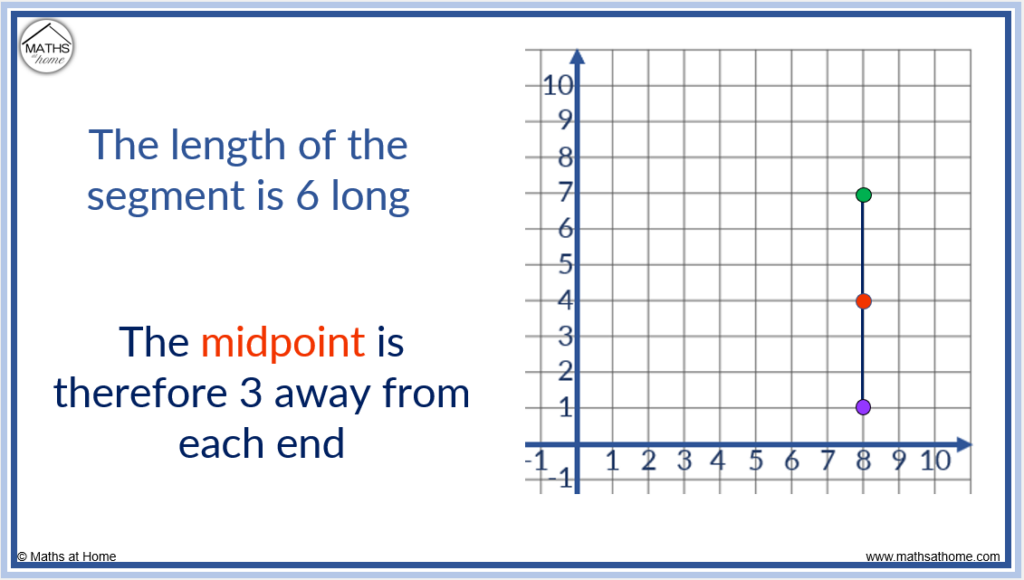
Midpoint of a Vertical Line Segment
The midpoint of a vertical line segment will have the same x-coordinate as any other point on the line segment. The y-coordinate will be half way in between the y-coordinates at each end of the line segment. Simply divide the length of the line segment by 2 and count this distance from either of the end points.
For example, the line segment from (8, 1) to (8, 7) is 6 long.
Therefore the midpoint is found 3 places in from either end point.
The midpoint is at (8, 4). This has the same y-coordinate as each end point.
How to Find the End point When Given the Midpoint
Find the difference between the start point of the line segment and the midpoint for both the x and y coordinates. Add this difference on to the midpoint coordinates to find the coordinates of the end point of the line segment.
Example
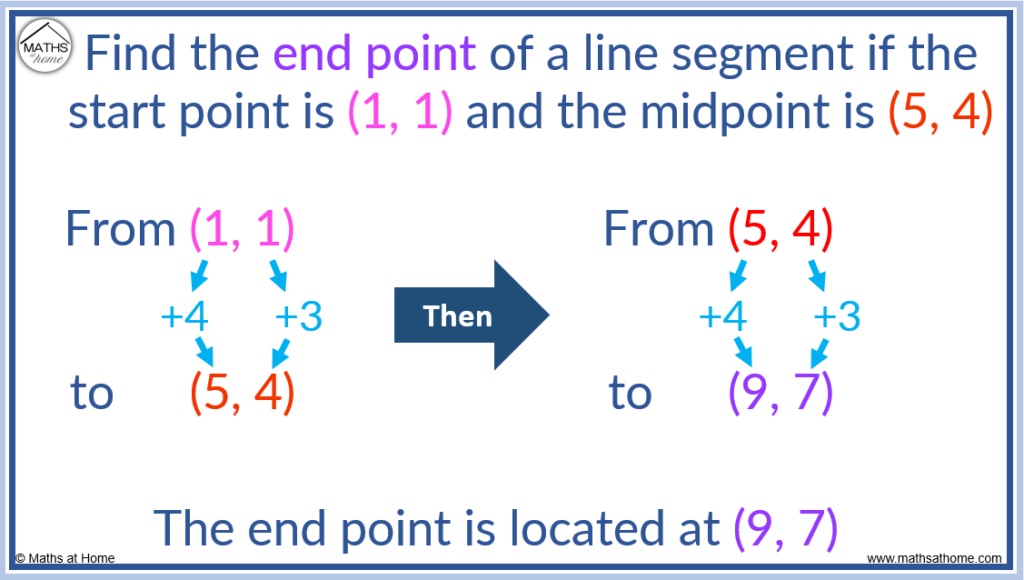
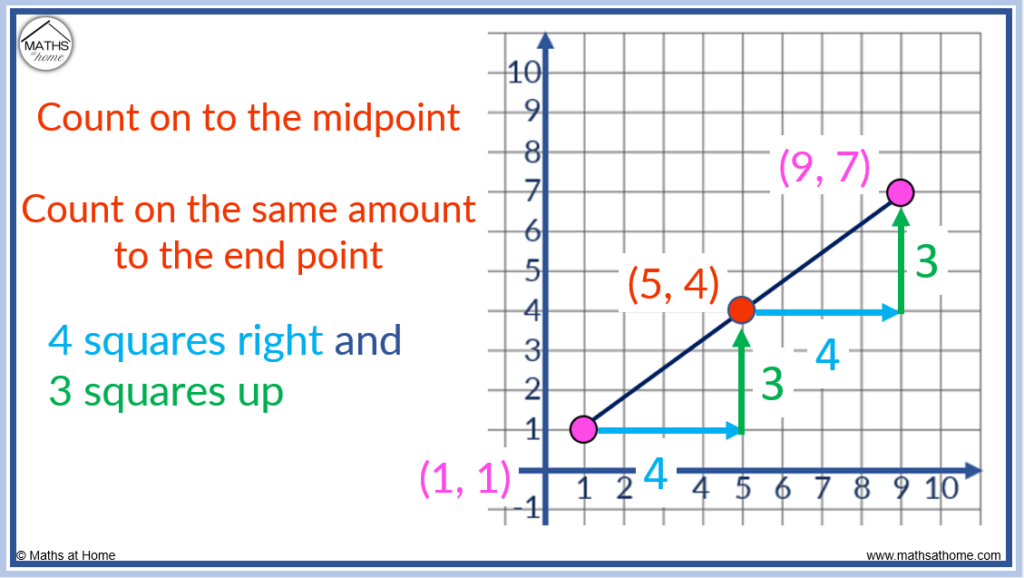
Find the end point of a line segment if the start point is (1, 1) and the midpoint is (5, 4).
The difference from (1, 1) to (5, 4) is (4, 3).
4 has been added to to the x-coordinate and 3 has been added to the y-coordinate.
To find the end point, add the distance from the start point to the midpoint on to the midpoint.
(4, 3) is added to (5, 4) to obtain (9, 7).
The end point is located at (9, 7).
How to Find the Midpoint with 3D Coordinates
In 3D, the midpoint between the two coordinates (x1, y1, z1) and (x2, y2, z2) is located at (x1+x2)/2, (y1+y2)/2, (z1+z2)/2.
Formula for the midpoint of a line segment in three dimensions
Example
Find the midpoint between the two 3D coordinates (3, 0, 6) and (5, 4, 10).
Therefore becomes
.
Therefore the midpoint is found at .
Alternatively, simply add the coordinates of (3, 0, 6) and (5, 4, 10) to obtain (8, 4, 16). Then halve this to obtain (4, 2, 8).

