Video Lesson: How to Calculate the Angle and Slope of a Line
In this lesson, the angle of inclination of a line will be calculated from the gradient and vice versa.
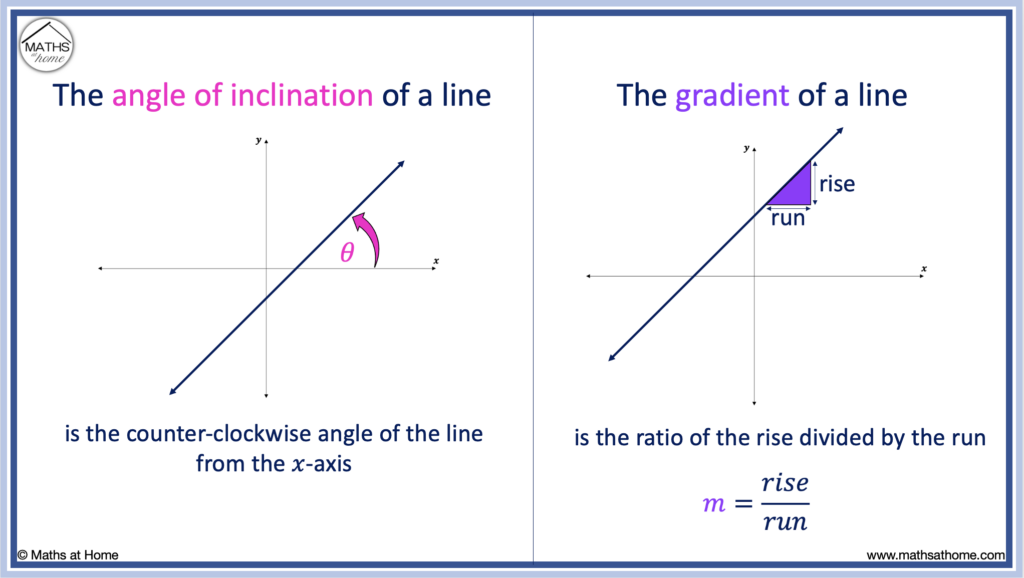
The angle of inclination of a line is the angle that the line makes with the positive 𝑥-axis. This angle is measured in a counter-clockwise direction from the axis as shown.
The gradient is the measure of the steepness of a line. It is calculate using the formula m = rise / run.
How to Calculate the Gradient of a Line from an Angle
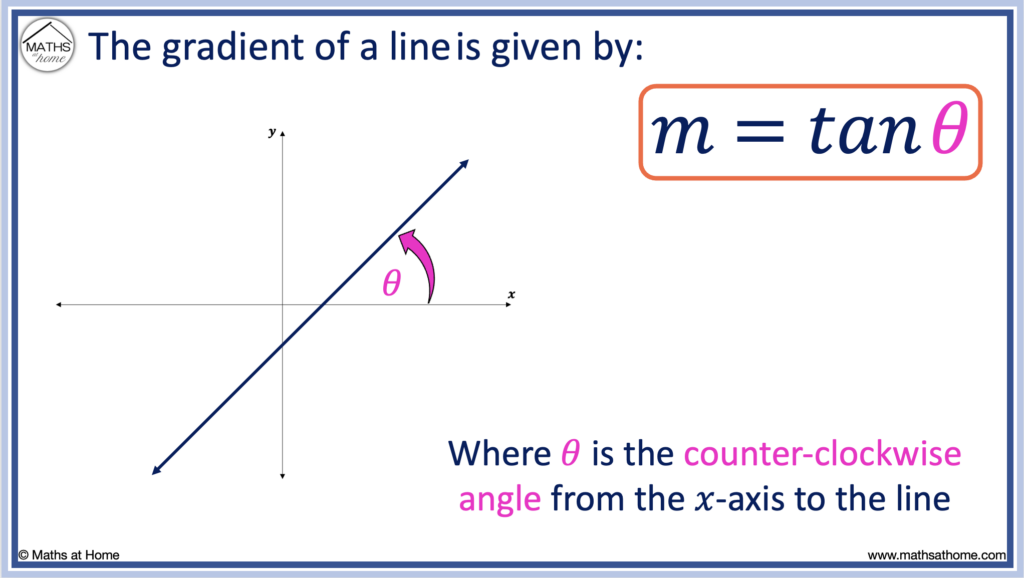
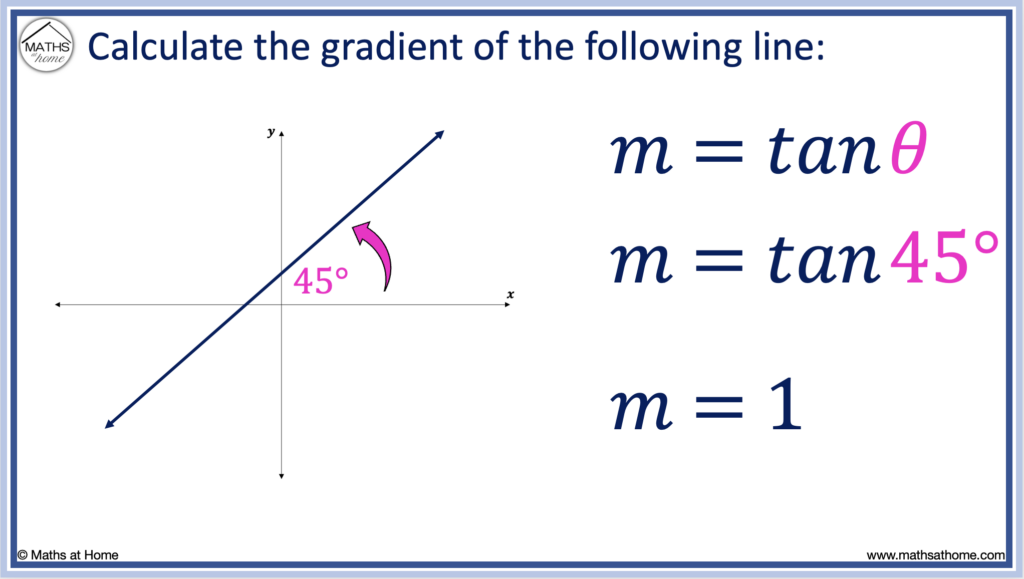
The gradient of a line is given by m = tan(θ), where θ is the counter-clockwise angle from the 𝑥-axis and the line. For example, a line that makes an angle of 45° with the 𝑥-axis has a gradient of m = tan(45°). Evaluating tan(45°) = 1, the gradient of this line is equal to 1.
m = tanθ
The formula for the gradient of a line from its angle of inclination with the positive 𝑥-axis
The angle θ must be the angle measured counter-clockwise from the positive 𝑥-axis to the line.
Neither the value of the 𝑥 or y-axis intercepts affect the value of the gradient. The gradient of a straight line is only determined by its angle of inclination.
The angle of inclination, θ, can be measured in either degrees or radians. However, tan(θ) must be evaluated in the same units that the angle, θ, is measured in.
For example, tan(45°) = 1 and so, the gradient of a line with an angle of inclination of 45° is 1.
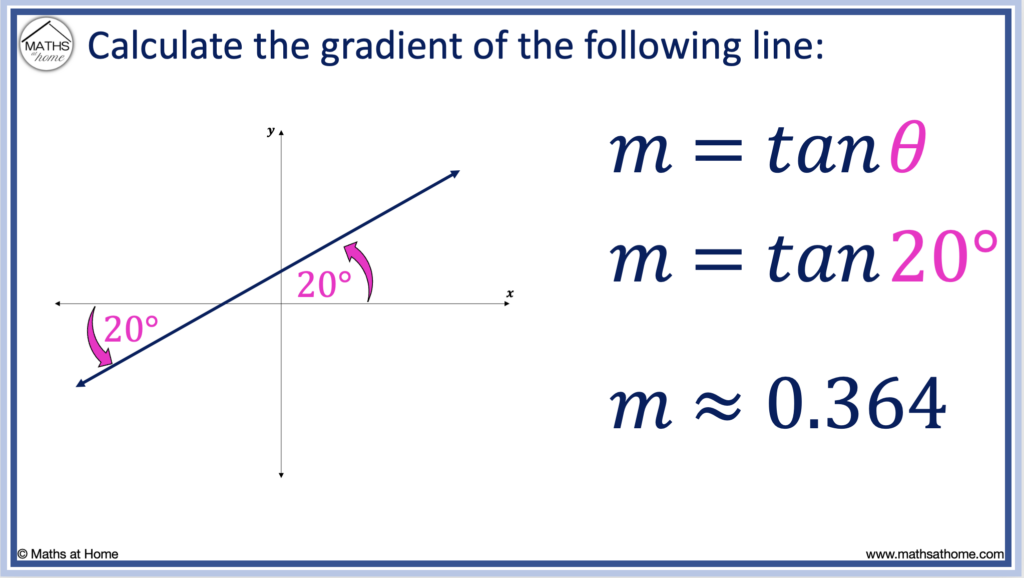
In this example, the angle that the line makes with the positive 𝑥-axis is 20°.
Therefore θ = 20°.
Therefore, the gradient of the line is found as tan(20°), which is approximately equal to 0.364.
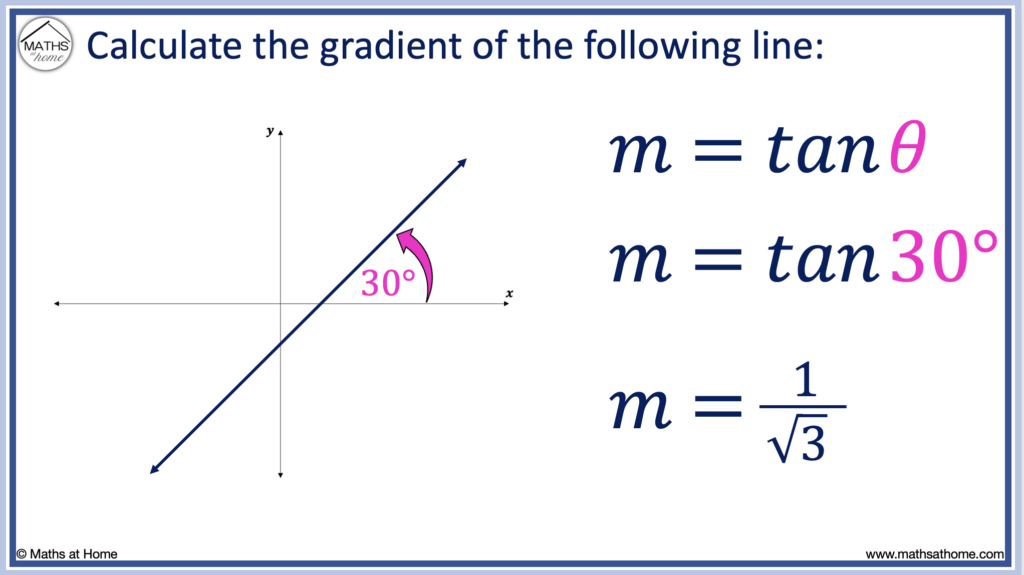
For example, a line that has an angle of inclination of 30° has a gradient of tan(30°).
tan(30°) can be evaluated exactly as 1/√3 which is approximately 0.577.
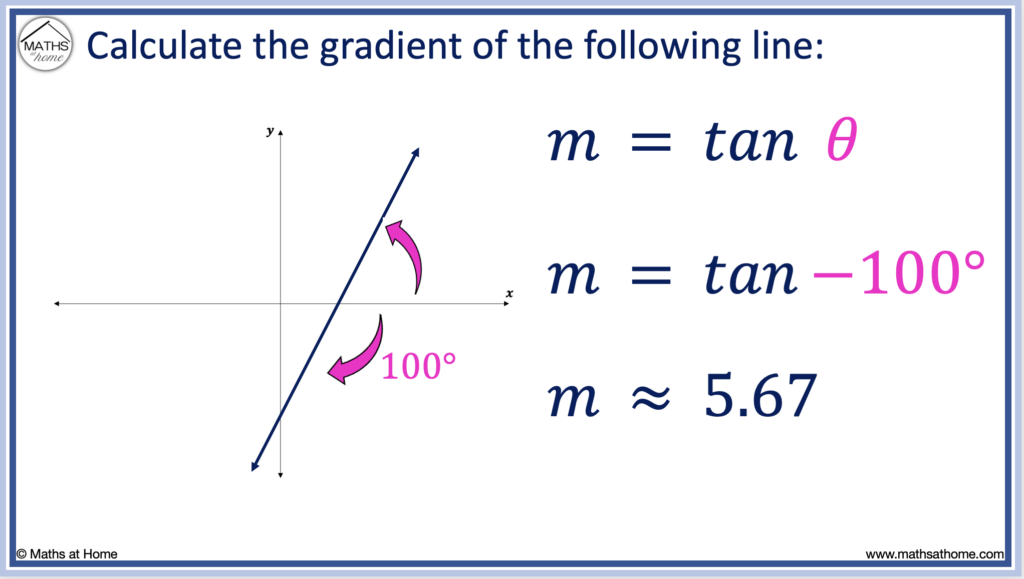
In this example, the line makes an angle of inclination that is 100° below the positive 𝑥-axis. This angle is 100° clockwise from the positive 𝑥-axis.
The angle of inclination must be measured in a counter-clockwise direction from the positive 𝑥-axis.
Angles of inclination in a clockwise direction from the positive 𝑥-axis are taken as negative.
Therefore θ = -100°.
Therefore, the gradient of the line is calculated as tan(-100°), which equals approximately 5.67.
The gradient of this line is approximately 5.67.
Slope of a Line from its Angle Calculator
This calculator calculates the slope of a line from its angle of incidence. Enter the angle of incidence in degrees and the calculator will calculate the gradient of the line.
How to Calculate the Angle of a Line from its Slope
To calculate the angle of incidence of a line from its slope, use the formula θ = tan-1(m), where m is the slope. For example, a line with a gradient of 2 makes an angle of tan-1(2) ≈ 63.4° with the horizontal 𝑥-axis.
θ = tan-1
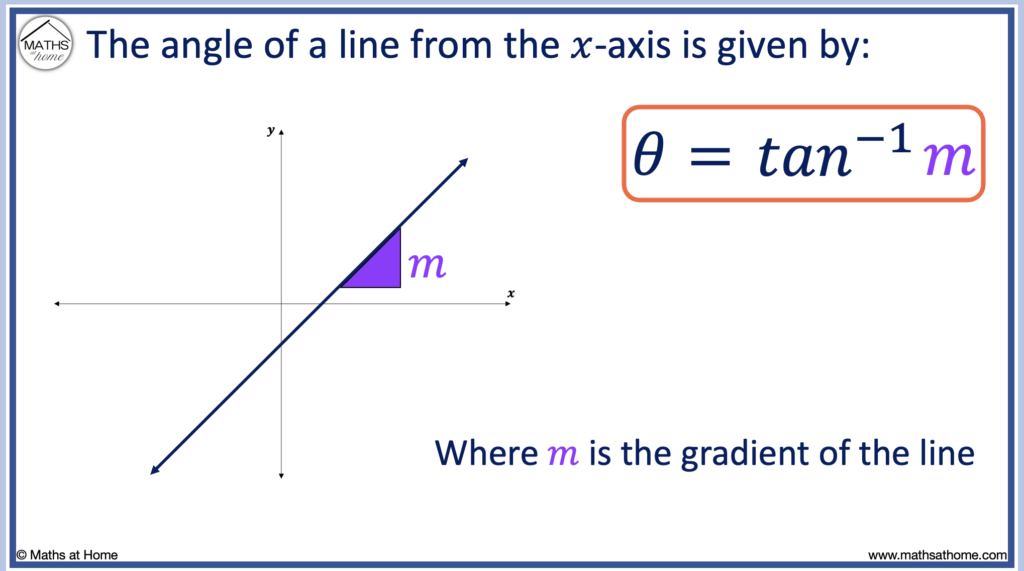
θ = tan-1(m)
Formula for calculating the angle of incidence of a line given its gradient
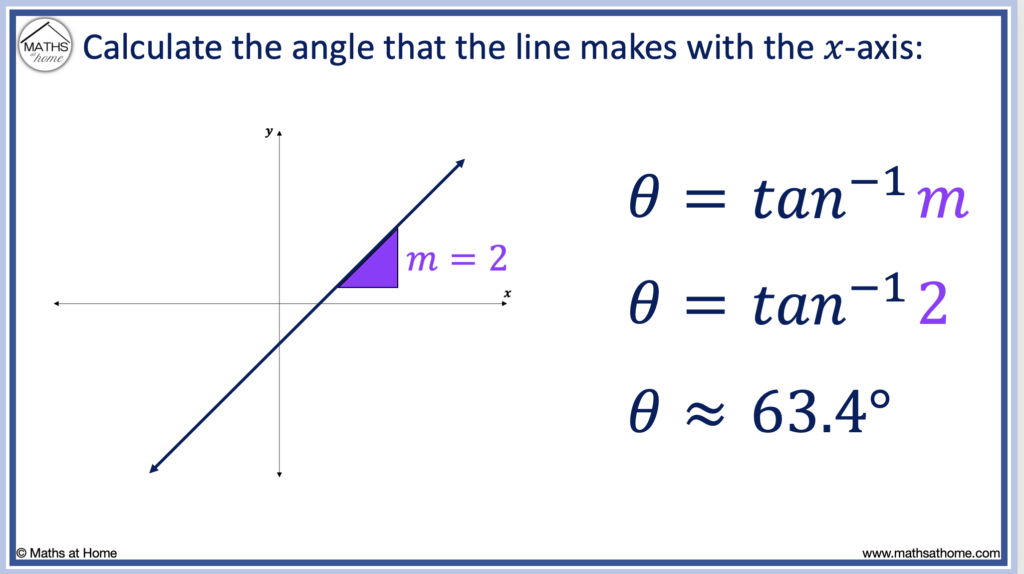
In the example below, the line has a gradient of 2.
Therefore, m = 2.
The angle of incidence of the line is given by θ = tan-1(m).
Therefore, we evaluate θ = tan-1(2) and so, θ ≈ 63.4°.
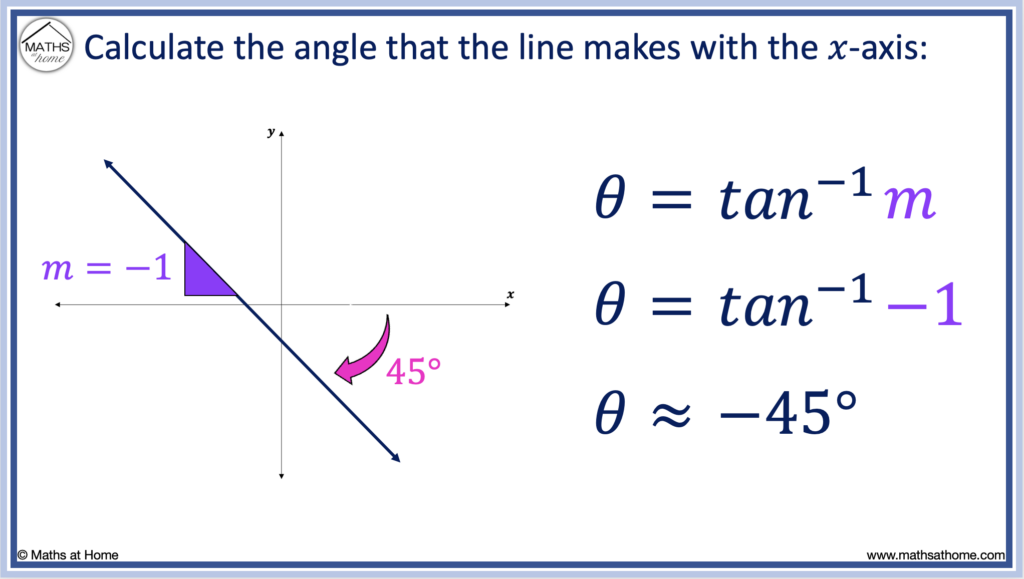
In the example below, the gradient of the line is given by m = -1.
Therefore, θ = tan-1(m) becomes θ = tan-1(-1).
Evaluating this, tan-1(-1) = -45°.
Angles of inclination are measured from the positive 𝑥-axis in the counter-clockwise direction.
Therefore, an angle of -45° means that the line makes an angle of 45° below the 𝑥-axis in the clockwise direction as shown on the diagram below.
Angle of a Line from the Slope Calculator
This calculator calculates the angle of incidence of a line from its slope. Simply enter the value of the gradient to calculate the value of the angle.
How to Calculate the Angle of a Line Between Two Points
To calculate the angle of a line from two points, first calculate the gradient using the formula m = (y2 – y1) / (𝑥2 – 𝑥1). Then calculate the angle using θ = tan-1(m).
For example, calculate the angle of the line passing through (1, 2) and (4, 8).
Firstly, the gradient is calculated using m = (y2 – y1) / (𝑥2 – 𝑥1).
The points (1, 2) and (4, 8) are labelled as (𝑥1, y1) and (𝑥2, y2).
Therefore: 𝑥1 = 1, y1 = 2, 𝑥2 = 4 and y2 = 8.
m = (y2 – y1) / (𝑥2 – 𝑥1) becomes m = (8 – 2) / (4 – 1).
Evaluating this, m = 6 / 3 which equals 2. The gradient is therefore equal to 2.
Secondly, the angle of the line is found by substituting m = 2 into the formula θ = tan-1(m).
tan-1(2) ≈ 63.4° and so, this is the angle of incidence of the line.

Angle of a Line Between Two Points Calculator
This calculator calculates the angle of a straight line from two known points on the line: (𝑥1, y1) and (𝑥2, y2).
Simply enter the 𝑥 and y coordinates of point 1 and then the 𝑥 and y coordinates of point 2 in the calculator below.
angle from rise over run
