Video Lesson: How to Find the Inverse of a 2×2 Matrix
What is the Inverse of a Matrix?
The inverse of a matrix is another matrix that when multiplied by the original matrix results in the identity matrix. For any given matrix, A, its inverse is denoted as A-1. Therefore AA-1=I and A-1A=I.
It is possible to add, subtract and multiply matrices but not divide them.
Instead, to ‘divide’ by a matrix, we multiply by its inverse.
Multiplying a matrix by its own inverse matrix results in the identity matrix. The identity matrix is the matrix equivalent of the number 1. The identify matrix is a square matrix containing all zeros except for the leading diagonal (top-left to bottom-right) which contains only the number 1.

For example, the matrix has an inverse matrix of
.
When the two matrices are multiplied together, the result is the identity matrix, .

Multiplying a matrix by its reciprocal is like multiplying a normal integer by its reciprocal.
For example, multiplying the number 5 by its reciprocal of 1/5 results in one. .
The identity matrix is the matrix equivalent of the number 1.
How to Find the Inverse of a 2×2 Matrix
To find the inverse of a 2×2 matrix, swap the numbers on the top-left to bottom-right diagonal with each other, change the signs of the numbers on the top-right to bottom-left diagonal and then divide all numbers by the determinant (ab-bd).
For any 2×2 matrix: , its inverse is given by the formula:
Formula for the inverse of a 2×2 matrix, where
The value of is known as the determinant of the matrix.

For example, calculate the 2×2 inverse matrix of the matrix .
Comparing this matrix to , we can see that:
- a = 2
- b = 1
- c = 4
- d = 5
Therefore, the formula of becomes:
.
Notice that inside the matrix, the 5 and the 2 on the leading diagonal swapped places and the 1 and the 4 on the non-leading diagonal became -1 and -4.
Evaluating the determinant on the bottom of the fraction: .
Therefore, the inverse matrix becomes: .
This can be simplified by multiplying all elements within the matrix by to obtain:
.

Here is an alternative method to find the matrix inverse.
The steps to calculate the inverse of a 2×2 matrix are:
- Calculate the adjoint by switching the elements on the leading diagonal and changing the sign of the elements on the non-leading diagonal.
- Calculate the determinant by subtracting the product of the non-leading diagonal from the product of the leading diagonal.
- Divide the adjoint of the matrix by its determinant.
For example, find the inverse matrix of .
Step 1. Calculate the adjoint by switching the elements on the leading diagonal and changing the sign of the elements on the non-leading diagonal
The adjoint of matrix A is found by switching the elements on the leading diagonal (top left to bottom right) and then changing the sign of the elements on the non-leading diagonal.
The elements on the leading diagonal are 1 and 3/2. We switch their positions with each other.
The elements on the non-leading diagonal are -2 and –1/2. They are both negative and so when their signs are changed, they become 2 and 1/2.
Therefore the adjoint of A is: .
Step 2. Calculate the determinant by subtracting the product of the non-leading diagonal from the product of the leading diagonal
The leading diagonal elements are 1 and 3/2. Finding their product means to multiply them together so we get .
The non-leading diagonal elements are -2 and –1/2. Their product is .
We subtract the product of the non-leading diagonal from the product of the leading diagonal to obtain: .
Therefore, the determinant is equal to .
Step 3. Divide the adjoint of the matrix by its determinant
The inverse of the matrix is equal to the adjoint matrix, ,divided by the determinant,
.
.
This results in each of the elements inside the adjoint matrix doubling in size to obtain:
.

Formula for the Inverse of a 2×2 Matrix
For any 2×2 matrix A = [a, b | c, d], the formula for the inverse matrix is A-1 = [1÷(ad-bc)]× [d, -b | -c, a].
Formula for the inverse of a 2×2 matrix, where

Since is known as the determinant of the matrix, the formula for the 2×2 inverse matrix can be written as:
Formula for the inverse of a 2×2 matrix
Alternatively, the formula can be written as:
Formula for the inverse of a 2×2 matrix

The easiest shortcut for calculating the inverse of a 2×2 matrix is A-1 = [ 1 ÷ ( ad – bc ) ] × [d, -b, -c, a].
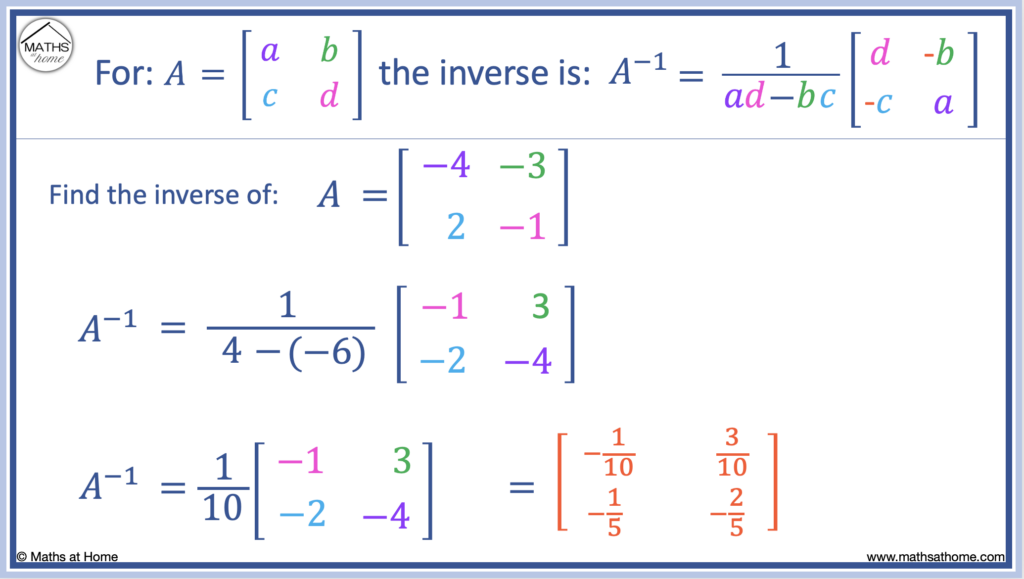
For example, find the inverse of .
In this case:
a = -4, b = -3, c = 2 and d = -1.
We substitute into the formula: A-1 = [1÷(ad-bc)]× [d, -b, -c, a] to obtain:
A-1 = [ 1 ÷ ( (-4×-1)-(-3×2) ) ]× [-1, 3, -2, -4].
This can be evaluated as: A-1 = [ 1 ÷ 10 ]× [-1, 3, -2, -4].
We can write the inverse matrix as: .
Multiplying each element in the matrix by 1/10 (or by dividing them by 10), we obtain:
.
Matrices with No Inverse
A matrix does not have an inverse if it has a determinant equal to zero. A matrix that does not have an inverse is called non-invertible or singular.
For a matrix to have an inverse:
- It must be a square matrix.
- Its determinant must not be equal to zero.
A non-square matrix is a matrix in which the number of columns is not equal to the number of rows. Only square matrices, in which the number of columns is equal to the number of rows, have inverses. Non-square matrices do not have an inverse.
For any 2×2 matrix of the form , it does not have an inverse if
.
That is because the formula for the inverse is and we cannot have 0 on the denominator of a fraction because it would result in dividing by zero.
For example, find the inverse of .
The determinant is equal to (4×3) – (2×6) which equals 12 – 12 = 0.
This matrix has no inverse.

For a matrix to have an inverse, it must be a 1:1 matrix and one row must not be a multiple of another row.
In the example above, we can see that the bottom row of [6 3] is 1.5 times the top row [4 2].
Another example of a matrix that has no inverse is .
We can see that the bottom row is twice as large as the top row.
We will call the proposed inverse of this matrix B, where.
Any matrix multiplied by its inverse will result in the identity matrix, .
Therefore, and therefore,
.
Multiplying the matrices out, we see that and
.
This results in a contradiction, since there is no solution for which both of these statements are true.
This means that B cannot be the inverse of A and therefore, A cannot have an inverse.
Self-Inverse Matrices
A self-inverse matrix is a matrix that is identical to its inverse matrix. That is, A2 = I. A matrix that is its own inverse is called involutory.
An example of a self-inverse matrix is .
Therefore we say that if , then
.
The identity matrix is a self-inverse matrix since II=I. The identity matrix multiplied by itself produces the identity matrix.
.
We say that .
Inverse of a 2×2 Matrix Using Elementary Row Operations
To find the inverse of a 2×2 matrix, A, using row operations, first write the matrix as A=IA, where I is the identity matrix. Then apply a sequence of row operations to obtain the form I=BA, where B is the inverse matrix.
When performing row operations, we can subtract multiples of a row from another and we can multiply an entire row by a number.
The aim to to turn the first matrix into the identity matrix.
For example, find the inverse of .
Here, row 1 (R1) = [1 2] and row 2 (R2) = [3 4].
- We first write the equation in the form A=IA like so:
.
- Now we do row operations so that the matrix before the equals sign becomes an identity matrix.
We first do the row operation: R2 = R2 – 3R1 to obtain .
Now we do the row operation: R2 = R2 to obtain
.
Finally, we do the row operation: R1 = R1 – 2R2 to obtain .
Now that the row reduction is complete, the inverse matrix is found just after the equals sign.
Therefore .
Here is another example.
Find the inverse of .
- We first write the matrix equation as
.
- Now we do row operations so that the matrix before the equals sign becomes an identity matrix.
First we do: R1 = R1 so that:
.
Now R2 = R2 + 7R1, so that: .
Now R2 = -3R2, so that: .
Now R1 = R1 – R2, so that:
.
Therefore, the inverse matrix is .
Proof of the Inverse of a 2×2 Matrix
The general formula for the inverse of a 2×2 matrix can be derived by writing AA-1 = I and then solving the resulting set of equations.
For example, we will call our matrix .
We will call the proposed inverse matrix
Since any matrix multiplied by its inverse is the identity matrix, we obtain: .
Multiplying out, we obtain the following equations:
Equation 1:
Equation 2:
Equation 3:
Equation 4:
Multiplying Equation 1 by d, we obtain .
Multiplying Equation 3 by -b, we obtain .
Adding these results, we obtain .
We can rearrange this to obtain and therefore,
Multiplying Equation 2 by -d, we obtain .
Multiplying Equation 4 by b, we obtain .
Adding these results, we obtain .
We can rearrange this to obtain and therefore:
Multiplying Equation 1 by c, we obtain .
Multiplying Equation 3 by -a, we obtain .
Adding these results, we obtain .
We can rearrange this to obtain and therefore:
.
Multiplying Equation 2 by -c, we obtain .
Multiplying Equation 4 by a, we obtain
Adding these results, we obtain .
We can rearrange this to obtain and therefore:
.
Putting the results for w, x, y and z back into our inverse matrix, , we obtain:
.
We can factor out the to obtain the final derived formula:
.
How to Find the Inverse of a 2×2 Matrix on a Calculator:
Inverse Matrix on a Ti-84
To find the inverse of Matrix A on the Ti84 Calculator:
- Press [2nd], [𝑥-1] to open the ‘matrix’ screen.
- Highlight [A] and press [ENTER].
- Press [𝑥-1] so that ‘[A]-1 is written.
- Press [ENTER] to obtain the inverse matrix.
Inverse Matrix on a Casio fx-CG50
To find the inverse of Matrix A on the Casio fx-CG50 calculator:
- Press [shift], [2] to type ‘Mat’.
- Press [ALPHA] and select [A] so that ‘MatA’ is written.
- Press [^] and type ‘-1’ so that ‘MatA-1 is written.
- Press ‘EXE’ to calculate the inverse.
Solving a System of Equations Using an Inverse 2×2 Matrix
To solve a system of equations using an inverse matrix:
- Write matrix A containing the coefficients of 𝑥 and y with the values from each equation in a different row.
- Write matrix B containing the constant terms from each equation in their corresponding rows.
- Calculate the solution matrix as X = A-1B.
For example, solve the simultaneous equations:
Step 1. Write matrix A containing the coefficients of 𝑥 and y with the values from each equation in a different row.
In the first equation, we have 2𝑥 and 1y. Therefore the coefficients for the top row of the matrix are [2 1].
In the second equation, we have 4𝑥 and 5y. Therefore the coefficients for the bottom row are [4 5].
Therefore, matrix .
Step 2. Write matrix B containing the constant terms from each equation in their corresponding rows.
The constant terms are after the equals sign.
In the top row, we have 5.
In the bottom row we have 7.
Therefore matrix .
Step 3. Calculate the solution matrix as X = A-1B.
Previously, the equation was written as , where:
and
.
We rearrange to the form
by premultiplying both sides by the inverse of matrix A.
We use to obtain the solutions.
Since
, we find the inverse matrix as
.
Using we obtain
.
Multiplying these two matrices, we get .
The answer is therefore and
.

