How to Find a Vector Perpendicular to a Plane

Video Lesson: How to Find a Vector Perpendicular to a Plane

How to Find a Vector Perpendicular to a Plane from 3 Given Points

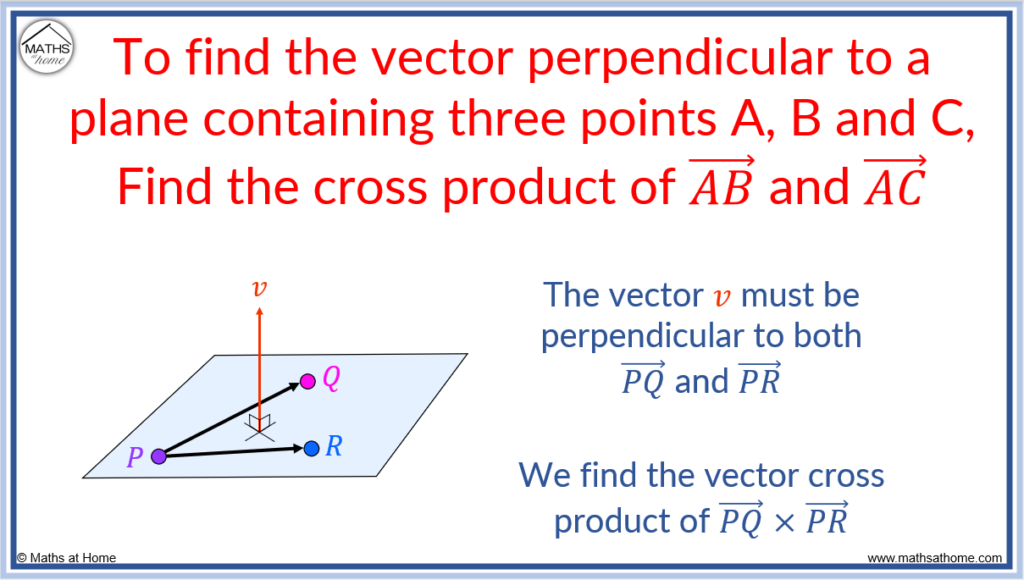
To find a vector perpendicular to a plane from three given points A, B and C:

  1. Calculate the vectors AB and AC.
  2. Calculate the cross product of the vectors AB and AC.

A plane is a flat surface that extends forever with zero thickness. A plane can be defined if the location of three points on the plane are known.

The vector perpendicular to a plane is one which intersects the plane at 90 degrees. Alternate names for this are the normal vector or orthogonal vector. These names will be used interchangeably throughout.

The perpendicular vector is at right-angles to the plane which means that it is also at right-angles with any other vectors that lie on the plane such as A B right arrow and A C right arrow.

how to find the vector perpendicular to a plane with 3 points

For example, find a vector which is perpendicular to the plane passing through the points P(2, 0, -1), Q(1, 1, 3) and R(0, -1, 2).

Step 1. Calculate the vectors A B right arrow and A C right arrow

In this case we calculate the vectors P Q right arrow and P R right arrow.

To calculate P Q right arrow we subtract the coordinates of P from the coordinates of Q.

the 3 by 1 column matrix 1 1 3 minus the 3 by 1 column matrix 2 0 negative 1 equals the 3 by 1 column matrix negative 1 1 4 and therefore P Q right arrow equals the 3 by 1 column matrix negative 1 1 4.

To calculate P R right arrow we subtract the coordinates of P from the coordinates of R.

the 3 by 1 column matrix 0 negative 1 2 minus the 3 by 1 column matrix 2 0 negative 1 equals the 3 by 1 column matrix negative 2 negative 1 3and therefore P R right arrow equals the 3 by 1 column matrix negative 2 negative 1 3.

step 1 of finding a vector normal to a plane

Step 2. Calculate the cross product of the vectors A B right arrow and A C right arrow

In this case we calculate the cross product of the vectors P Q right arrow and P R right arrow.

The result of the cross product will be the the vector that is normal to the plane.

This is because the cross product of two vectors is perpendicular to the two vectors. Since the two vectors P Q right arrow and P R right arrow lie in the plane, any vector perpendicular to both of these vectors will also be perpendicular to the plane.

The cross product of the 3 by 1 column matrix negative 1 1 4 and the 3 by 1 column matrix negative 2 negative 1 3 is found by writing them above each other like so the determinant of the 3 by 3 matrix Row 1: i j k Row 2: negative 1 1 4 Row 3: negative 2 negative 1 3.

To find the i component of the cross product, we first cover up the values in the i column and write down the remaining numbers. We will find the determinant of the remaining 2 times 2 matrix.

Covering the i column, we are left with the determinant of the determinant of the 2 by 2 matrix Row 1: 1 4 Row 2: negative 1 3.

the cross product tells us the normal vector to a plane
calculating the cross product of two vectors part 1

To find the j component, we cover the j column and we are left with the determinant of negative the determinant of the 2 by 2 matrix Row 1: negative 1 4 Row 2: negative 2 3.

Notice we place a negative sign in front of this determinant. The i and k components do not have this but the j component does. This is part of the cross product calculation method.

To find the k component, we cover the k column and are left with the determinant of the determinant of the 2 by 2 matrix Row 1: negative 1 1 Row 2: negative 2 negative 1.

calculating the cross product of two vectors part 2
calculating the cross product of two vectors part 3

The cross product of P Q right arrow equals the 3 by 1 column matrix negative 1 1 4 and P R right arrow equals the 3 by 1 column matrix negative 2 negative 1 3 is therefore given as:

v equals the determinant of the 3 by 3 matrix Row 1: i j k Row 2: negative 1 1 4 Row 3: negative 2 negative 1 3 equals the determinant of the 2 by 2 matrix Row 1: 1 4 Row 2: negative 1 3 times i minus the determinant of the 2 by 2 matrix Row 1: negative 1 4 Row 2: negative 2 3 times j plus the determinant of the 2 by 2 matrix Row 1: negative 1 1 Row 2: negative 2 negative 1 times k

We now evaluate the 2 times 2 determinants in each component of the vector.

To calculate the determinants in each 2 times 2 matrix , multiply the top left number by the bottom right number and then subtract the top right number multiplied by the bottom left number.

  • For the i component: the determinant of the 2 by 2 matrix Row 1: 1 4 Row 2: negative 1 3 equals open paren 1 times 3 close paren minus open paren negative 1 times 4 close paren equals 7
  • For the j component: the determinant of the 2 by 2 matrix Row 1: negative 1 4 Row 2: negative 2 3 equals open paren negative 1 times 3 close paren minus open paren negative 2 times 4 close paren equals 5
  • For the k component: the determinant of the 2 by 2 matrix Row 1: negative 1 1 Row 2: negative 2 negative 1 equals open paren negative 1 times negative 1 close paren minus open paren negative 2 times 1 close paren equals 3

Therefore the vector normal to the plane is v equals 7 i minus 5 j plus 3 k.

This can be written as v equals the 3 by 1 column matrix 7 negative 5 3.

example of a question to find the normal vector to a plane from 3 points

Vector Normal to a Plane Formula

The formula for a vector normal to the plane ax+by+cz=d is n=<a, b, c>.

n right arrow equals is less than a. comma b comma c is greater than

The vector normal to the plane a. x plus b y plus c z equals d
formula for the vector normal to a plane

How to Find a Vector Normal to a Plane from its Equation

The vector normal to the plane ax+by+cz=d is equal to n=(a, b, c).

For example, the vector normal to the plane 3x+y-2z=12 is given by n=(3, 1, -2).

The coefficients of x, y and z in the equation of the plane form the i, j and k components of the normal vector.

The constant term of the equation of the plane does not affect the normal vector. This is because the constant term of the plane equation does not affect the orientation of the plane, rather it just affects its absolute position. The normal vector is only dependent of the orientation of the plane.

how to find the vector normal to a plane from its equation

The i component of the normal vector is given by the x coefficient.

We have 3x and so, the i component is 3.

The j component of the normal vector is given by the y coefficient.

We have y, which is the same as 1y and so, the j component is 1.

The k component of the normal vector is given by the z coefficient.

We have -2z and so, the k component is -2.

Here are some further examples of finding the normal vector to a plane from the equation.

Equation of the PlaneNormal Vector to the Plane
2x + 5y + 3z = 17<2, 5, 3>
3x – 2y – 5y = – 2<3, -2, -5>
x + y + z = 5<1, 1, 1>
4x – 3z = 10<4, 0, -3>
-2x + 5y – z + 10 = 0<-2, 5, -1>

How to Find a Unit Vector Perpendicular to a Plane

The unit vector normal to the plane ax+by+cz=d is given by n=<a, b, c>/√(a2+b2+c2).

n hat equals the fraction with numerator is less than a. comma b comma c is greater than and denominator the square root of a. squared plus b squared plus c squared

The formula for the unit vector normal to the plane
how to find the unit vector normal to a plane

For example, find the unit vector normal to the plane 5 x plus y minus 3 z equals 10.

In this example we have the following values which can be substituted into the formula n hat equals the fraction with numerator is less than a. comma b comma c is greater than and denominator the square root of a. squared plus b squared plus c squared:

  • a = 5
  • b = 1
  • c = -3

Therefore the unit vector normal to the plane is n hat equals the fraction with numerator is less than 5 comma 1 comma negative 3 is greater than and denominator the square root of 5 squared plus 1 squared plus open paren negative 3 close paren squared.

This simplifies to n hat equals the fraction with numerator is less than 5 comma 1 comma negative 3 is greater than and denominator the square root of 35.

This can be written as n hat equals is less than the fraction with numerator 5 and denominator the square root of 35 comma the fraction with numerator 1 and denominator the square root of 35 comma the fraction with numerator negative 3 and denominator the square root of 35 is greater than or n hat almost equals is less than 0.845 comma 0.169 comma negative 0.507 is greater than.

Vector Perpendicular to the xy Plane

The axis perpendicular to the xy plane is the z plane and so the unit vector perpendicular to the xy plane is ±k.

Vector Perpendicular to the yz Plane

The axis perpendicular to the yz plane is the x plane and so the unit vector perpendicular to the yz plane is ±i.

Vector Perpendicular to the xz Plane

The axis perpendicular to the xz plane is the y plane and so the unit vector perpendicular to the xz plane is ±j.

How to Find the Equation of a Plane from the Normal Vector and a Point

If a plane has a normal vector of <a, b, c> and passes through the point (p, q, r) then it has the cartesian equation of ax+by+cy=d, where d = ap+bq+cr.

equation of a plane from normal vector and point

For example:

Find the equation of the plane with normal vector the 3 by 1 column matrix 2 1 3 which passes through the point open paren negative 1 comma 1 comma 2 close paren.

From the normal vector:

  • a = 2
  • b = 1
  • c = 3

From the point on the plane:

  • p = -1
  • q = 1
  • r = 2

We substitute these values into the formula for the equation of the plane: a. x plus b y plus c z equals d, where d equals a. p plus b q plus c r.

First we calculate d equals 2 times negative 1 plus 1 times 1 plus 3 times 2 to find that d equals 5

Then the equation of the plane a. x plus b y plus c z equals d is found as 2 x plus y plus 3 z equals 5.

2 x plus y plus 3 z equals 2 times negative 1 plus 1 times 1 plus 3 times 2

Proof of the Equation of a Plane from a Normal and a Point

r is the position vector of any point on the plane and a is the position vector of a known point on the plane.

Therefore r minus a. describes any vector on the plane from the known point a to any point r.

n is perpendicular to any vector in the plane therefore the dot product of n and any vector on the plane is equal to zero.

n times open paren r minus a. close paren equals 0

This can be rearranged to give n times r equals n times a.

If n equals the 3 by 1 column matrix a. b c , r equals the 3 by 1 column matrix x y z and a. equals the 3 by 1 column matrix p q r, then the equation n times r equals n times a. becomes:

a. x plus b y plus c z equals a. p plus b q plus c r

This can be written as a. x plus b y plus c z equals d where d equals a. p plus b q plus c r