The Discriminant Video Lesson
What is the Discriminant of a Quadratic Equation?
The discriminant is the part of the quadratic formula found within the square root. For a quadratic of the form a𝑥2 + b𝑥 + c, its discriminant is b2 – 4ac. A quadratic equation has 2, 1 or 0 solutions depending if the value of the discriminant is positive, zero or negative respectively.

The discriminant, b2 – 4ac is represented by the delta symbol, Δ.
The discriminant formula is Δ = b2 – 4ac, where a is the coefficient of 𝑥2, b is the coefficient of 𝑥 and c is the constant term of a quadratic.
For example, calculate the discriminant of y = 𝑥2 + 5𝑥 + 2.
We have one 𝑥2. The coefficient of 𝑥2 is 1. Therefore a = 1.
The coefficient of 𝑥 is 5. Therefore b = 5.
The constant term is 2. Therefore c = 2.

We substitute the values of a = 1, b = 5 and c = 2 into the formula for the discriminant, b2 – 4ac.
b2 = 52 = 25
and 4ac = 4 × 1 × 2 = 8.
b2 – 4ac becomes 28 – 8 = 17. The discriminant is 17.
The discriminant is important because it tells us how many solutions any quadratic equation has.
- If the discriminant is a positive number, there will be 2 solutions.
- If the discriminant is zero, there will be 1 solution.
- If the discriminant is a negative number, there will not be any real solutions.

The number of solutions to a quadratic equation tells us the number of roots of the quadratic equation. The roots of a quadratic equation are the locations where the quadratic graph crosses the 𝑥-axis. They are the 𝑥-axis intercepts.
The following table shows the number of roots for a positive, negative or zero discriminant.
| Value of the discriminant | Number of Roots | |
| > 0 | Positive | Two |
| = 0 | Zero | One |
| < 0 | Negative | Zero |
How to Calculate the Discriminant
To calculate the discriminant of a quadratic equation, the formula is b2 – 4ac. Substitute the values of a, b and c after reading them from a quadratic equation of the form a𝑥2 + b𝑥 + c. For example, for 𝑥2 – 3𝑥 + 4, a = 1, b = -3 and c = 4. b2 = 9 and 4ac = 16. The discriminant, b2 – 4ac = – 7.
When calculating the discriminant it is important to consider these key points:
- b2 is always positive. When we square a negative number, it gives us a positive result.
- If 4ac is negative then we need to perform an addition. When we subtract a negative number, an addition takes place.

- Find a, which is the coefficient of 𝑥2.
- Find b, which is the coefficient of 𝑥.
- Find c, which is the constant term.
- Square the b value to find b2.
- Multiply 4 × a × c to find 4ac.
- Use these values to calculate b2 – 4ac.
Discriminant Calculator
To use the discriminant calculator:
- Read the coefficient of 𝑥2 to find ‘a’.
- Read the coefficient of 𝑥 to find ‘b’.
- Read the constant term which is ‘c’.
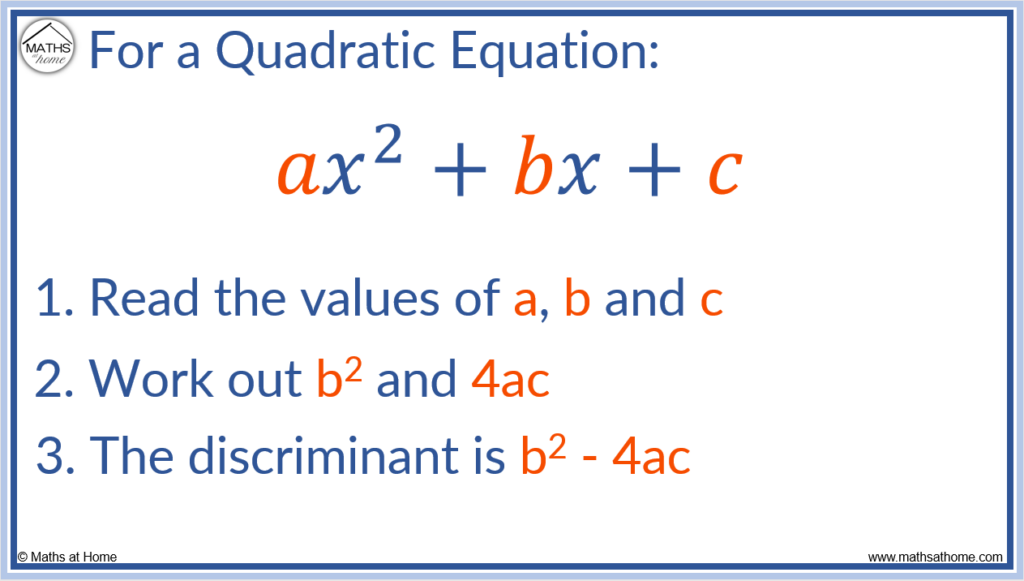
A Positive Discriminant
A positive discriminant means that the value of b2 – 4ac is greater than zero. A quadratic equation with a positive discriminant has exactly two solutions, which means that it has two 𝑥-axis intercepts. This means that the quadratic has 2 roots.
A positive value of the discriminant means that the graph of the quadratic equation must pass through the 𝑥-axis twice.
If the quadratic has a positive coefficient of 𝑥2 (a > 0), the graph is concave up and the minimum point will be below the 𝑥-axis as shown in the left image below.
If the quadratic has a negative coefficient of 𝑥2 (a < 0), the graph is concave down and the minimum point will be above the 𝑥-axis as shown in the right image below.

A positive value of the discriminant tells us that a quadratic has two unique solutions.
For example, the quadratic 𝑥2 – 4𝑥 + 3 = 0 has two solutions: 𝑥 = 3 and 𝑥 = 1.
This means that the quadratic equation crosses the 𝑥-axis at 𝑥 = 1 and 𝑥 = 3.
The discriminant value is 4, which is a positive number.

The square root of a positive number has both a positive and negative answer. Therefore the quadratic formula provides 2 different solutions.
If the discriminant is a perfect square, then the solutions to the quadratic equation are rational. This means that the solutions will be integers or can be written as fractions. If a discriminant is not a perfect square, the 2 solutions will be irrational. This is because the square root of this discriminant will be a surd.
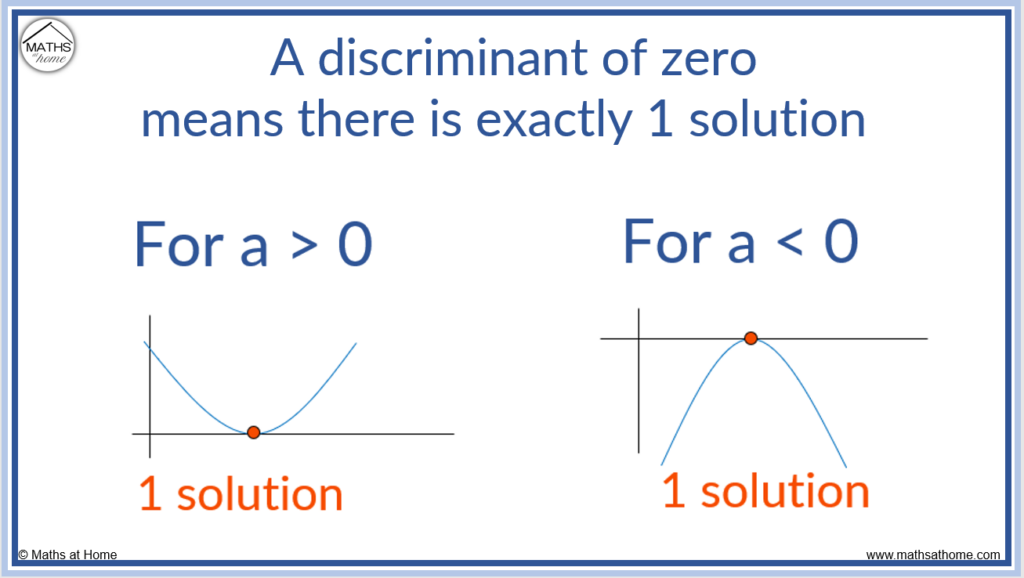
A Discriminant of Zero
A discriminant of zero means that the value of b2 – 4ac is equal to zero. A quadratic equation with a discriminant of zero has exactly one solution. This means that the graph of the quadratic just touches the 𝑥-axis at its minimum or maximum point.
A discriminant equal to zero means that the graph of the quadratic equation must touch the 𝑥-axis once. It cannot pass through the 𝑥-axis. Instead it just touches it at its one root.
If the quadratic has a positive coefficient of 𝑥2 (a > 0), the graph is concave up and the minimum point will touch 𝑥-axis as shown in the left image below.
If the quadratic has a negative coefficient of 𝑥2 (a < 0), the graph is concave down and the maximum point will touch the 𝑥-axis as shown in the right image below.
For a quadratic equation with a discriminant of zero, there will be exactly one solution. This is because the square root of the discriminant is taken as part of the quadratic formula. The square root of 0 is 0.
This means that we add or subtract 0 in the calculation, which causes the two answers to be the same.
The solution to a quadratic equation with a discriminant of zero is called a repeated root. This is because the same solution appears twice.

For example, the quadratic 𝑥2 – 4𝑥 + 4 = 0 has a = 1, b = -4 and c = 4.
b2 = 16 and 4ac = 16.
b2 – 4ac = 0 and the one repeated root of the quadratic equation is 𝑥 = 2.
A Negative Discriminant
A negative discriminant means that the value of b2 – 4ac is less than zero. When using the quadratic formula the square root of a negative cannot be found. There are no real solutions to the quadratic equation. The two solutions are complex and cannot be seen on a graph.
A negative discriminant means that the graph of the quadratic equation does not touch the 𝑥-axis.
If the quadratic has a positive coefficient of 𝑥2 (a > 0), the graph is concave up and the entirety of the graph is above the 𝑥-axis. All outputs of the graph are positive.
If the quadratic has a negative coefficient of 𝑥2 (a < 0), the graph is concave down and the entirety of the graph is below the 𝑥-axis. All outputs of the graph are negative.

For example, in the quadratic equation 𝑥2 – 3x + 5 =0, a = 1, b = -3 and c = 5.
b2 = 9 and 4ac = 20.
Therefore the discriminant b2 – 4ac = -11.
The square root of a negative number cannot be found and so, no real solutions can be found since we cannot complete the calculation.

The square root of -11 must be written in terms of the imaginary unit, i.
Therefore it is written as √11 i. This complex solution can be used.

The Discriminant from a Graph
The number of 𝑥-axis intercepts indicates the value of the discriminant:
- A graph with 2 𝑥-axis intercepts has a positive discriminant.
- A graph that touches the 𝑥-axis once has a discriminant of zero.
- A graph that does not touch the 𝑥-axis has a negative discriminant.

The Discriminant of a Cubic Equation
The discriminant of a cubic equation a𝑥3 + b𝑥2 + c𝑥 + d is b2c2 – 4ac3 – 4b3d – 27a2d2 + 18abcd. If the discriminant is positive, the cubic has 3 real roots. If it is negative, the cubic has one real root and two complex conjugate roots. If it is zero, at least two of the roots are equal.

| Cubic Discriminant Value | Meaning |
| Positive discriminant | 3 real roots |
| Discriminant of zero | At least one repeated root |
| Negative discriminant | 1 real root and 2 complex roots |
For example for the cubic 5𝑥3 + 2𝑥2 – 3𝑥 + 1, a = 5, b = 2, c = -3 and d = 1.
Using the cubic discriminant formula Δ = b2c2 – 4ac3 – 4b3d – 27a2d2 + 18abcd.
Δ = -671.

The cubic discriminant is negative and so, this cubic has 1 real root and 2 complex roots.
This means that its graph will only intersect the 𝑥-axis once.
