Composite Functions: A Complete Guide

Composite Functions Video Lesson

How to Find Composite Functions

To find a composite function:

1. Identify the outer and inner functions.
2. Write the outer function.
3. Substitute each 𝑥 with the inner function.
4. Simplify if necessary.

For example, if and , calculate .

1. Identify the outer and inner functions

For the composite function , the is on the inside of . It is the input to .

When written like this as , the outer function is the one written on the left and the inner function is on the right.

is the inner function and is the outer function.

2. Write the outer function

We write the outer function of .

3. Substitute each 𝑥 with the inner function

Every 𝑥 found within must be substituted with the inner function of .

and so, we replace the 𝑥 in with an 𝑥².

.

In this next example, we will keep and but this time calculate .

1. Identify the outer and inner functions

For the composite function , the is on the inside of . It is the input to .

When written as , the outer function is the one written on the left and the inner function is on the right.

is the inner function and is the outer function.

2. Write the outer function

We write the outer function of .

3. Substitute each 𝑥 with the inner function

Every 𝑥 found within must be substituted with the inner function of .

and so, we replace the 𝑥 in with 𝑥+3.

We must square all of 𝑥+3 and so, we first put it in brackets: (𝑥+3).

.

The Order of Composite Functions

The order of composite functions matters because a different order results in an entirely different function. Always substitute the inner function on the right into the outer function on the left. For example, if f(𝑥)=𝑥+3 and g(𝑥)=𝑥², f(g(𝑥))=𝑥²+3 and g(f(𝑥))=(𝑥+3)².

Always substitute the rightmost function into the function on its left.

For example, means that is substituted as an input into .

means that is substituted as an input into .

To remember the order of composite functions, draw a backwards-facing arrow from the rightmost function to the leftmost function.

Always substitute the function on the right into the function on the left.

Composite Functions with Numbers

Composite functions can be evaluated when a number is the input. Substitute the number into the functions from right to left. For example, if f(𝑥)=2𝑥+1 and g(𝑥)=𝑥², then gf(3) is found by substituting 3 into f(𝑥)=2𝑥+1 to get 7. Then substitute 7 into g(𝑥)=𝑥² to get 49. gf(3)=49.

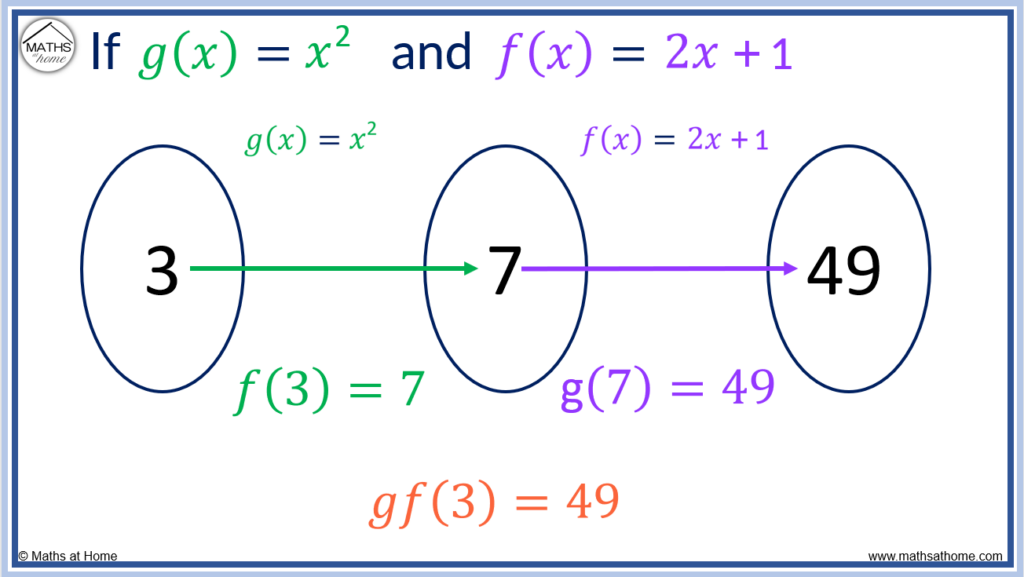
When the input to a composite function is a number, the resulting answer is also a number.

If the input to a composite function is 𝑥, the resulting answer will be another function.

When entering numbers into a composite function, it is important to evaluate each function from right to left.

In the example below, we first substitute 4 into g(𝑥) to get 2 and then substitute this output of 2 into f(𝑥) to get 11.

What Are Composite Functions?

A composite function is a function that is within another function. One function is substituted as the input to another function. For example f[ g(𝑥) ] means that g(𝑥) is substituted into every 𝑥 in the function of f(𝑥). The composite function f[ g(𝑥) ] is pronounced as ‘f of g of 𝑥’.

For example, in the composite function below, is substituted into to form .

A composite function is different to the functions it is composed of.

Composite Function Notation

Composite functions can be written in different notations.

A function, substituted as the input to another function, can be written as:

• 
• 
• 
• 

In mathematics, the circle symbol ∘ is used to indicate the composition of functions. For example (f∘g)(𝑥) means to take the output of g and substitute it into f.

is read as ‘f of g’ ‘f composed with g’, ‘f circle g’, ‘f round g’ or ‘f about g’.

Composite Function Arrow Diagram

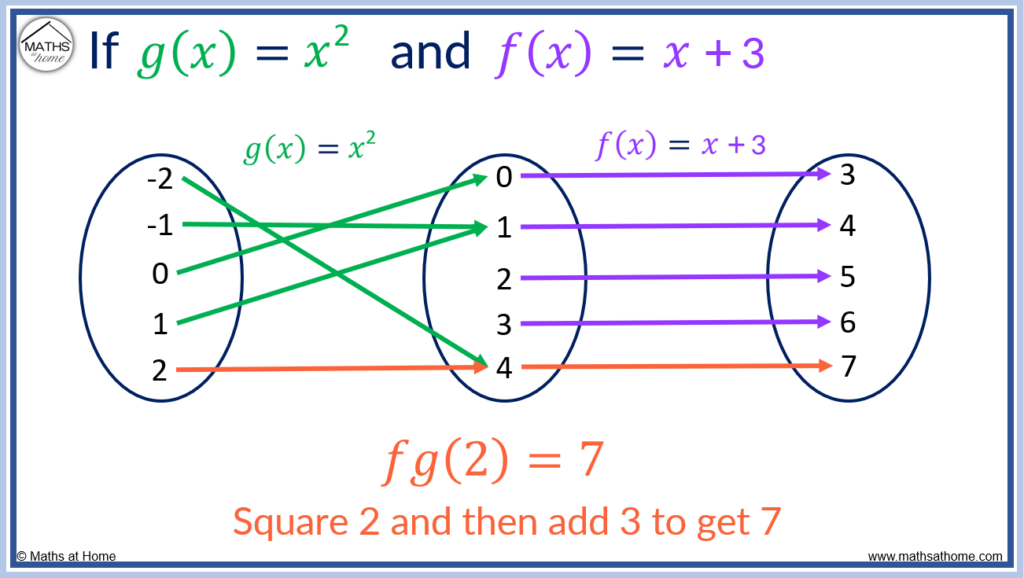
An arrow diagram can be used to explain composite functions. The inputs to the first function are listed on the left. Arrows connect these inputs to their outputs in the middle. These outputs are then the inputs to the next function which has its outputs shown on the right.

For example, to find using the arrow diagram below, follow the input of 2 shown with the red arrow.

The first arrow shows the function of . When we square 2 we get 4.

The second arrow leaves the 4 and reaches an output of 7. This is because the function tells us to add three to the previous output. 4 + 3 = 7.

Therefore =7.

Properties of Composite Functions

Composite functions have the following properties:

• The inverse of the composition of functions is equal to the composition of the inverse of both functions. (f∘g)^-1 = g^-1∘f^-1.
• The composition of one-to-one functions is also one-to-one.
• The composition of onto functions is also an onto function.
• Composite functions are assosciative. That is f∘(g∘h) = (f∘g)∘h.
• The composition of functions is generally not commutative. It cannot be assumed that f[g(x)] = g[f(x)].
• A composite function containing at least one even function will be even.
• A composite function composed of entirely odd functions will also be odd.

Composite Functions with 3 Functions

To find a composite function made of three functions, substitute the rightmost function into the middle function and then substitute this into the leftmost function. For example, if g(𝑥)=𝑥², f(𝑥)=3𝑥+1 and h(𝑥)=¹/_𝑥 then h(g(f(𝑥)))=¹/_(3𝑥+1)².

Arrows can be drawn from right to left to help remember the order of composite functions. In the example of h(g(f(𝑥))), the f function is substituted into the g function to form g(f(𝑥)).

g(f(𝑥)) = (3𝑥-1)².

This is then substituted into the h function of ¹/_𝑥. We replace the 𝑥 with (3𝑥-1)².

h(g(f(𝑥))) = ¹/_(3𝑥-1)².

Composite Function Examples

Composite Function Example with Square Roots

If g(𝑥) = 𝑥² + 5𝑥 and f(𝑥) = √𝑥, calculate g(f(𝑥)). Substitute √𝑥 into every 𝑥 found in the g(𝑥) function. g(f(𝑥)) = (√𝑥)²+5√𝑥. Here the √𝑥 and square operation cancel out to leave g(f(𝑥)) = 𝑥+5√𝑥.

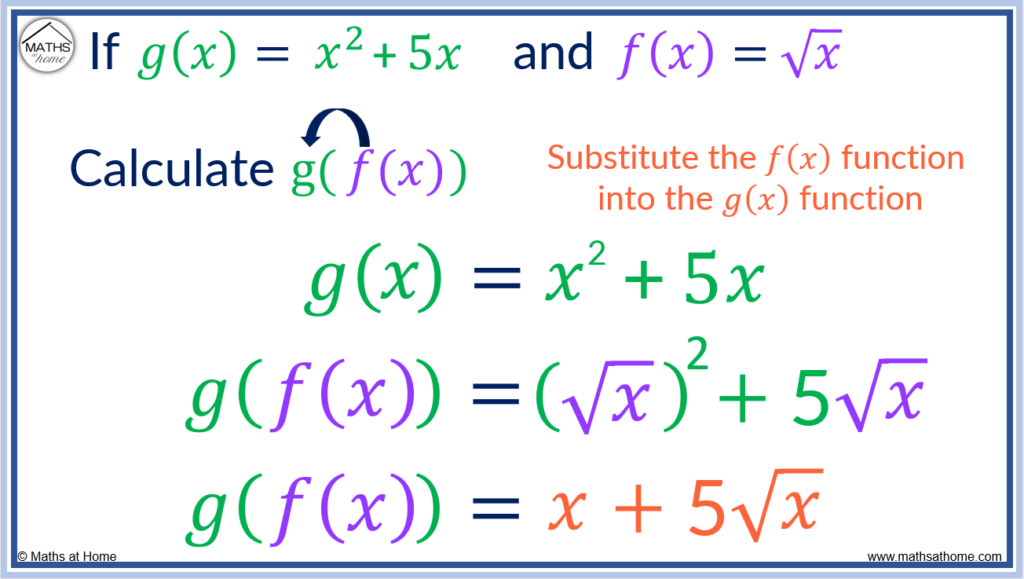
Composite Function Example with Fractions

If g(𝑥)=¹/_𝑥 and f(𝑥)=1-𝑥, find g(f(𝑥)). Substitute the f function into the 𝑥 in the g function. g(f(𝑥))=¹/_(1-𝑥). This composite function is written as a fraction.

Composite Function Example with Sin(𝑥)

If g(𝑥) = 2𝑥 + 1 and f(𝑥) = sin(𝑥), calculate f(g(𝑥)). Substitute 2𝑥+1 into every 𝑥 found in the f(𝑥) function. f(g(𝑥)) = sin(2𝑥+1).

Composite Function Example with e^𝑥

e^𝑥 and ln(𝑥) are inverse functions. When written as a composite function, these two functions cancel each other out. If g(𝑥)=e^𝑥 and f(𝑥)=ln(𝑥)-𝑥, calculate f(g(𝑥)). Each 𝑥 in f(𝑥) is replaced with e^𝑥 and so f(g(𝑥))=ln(e^𝑥)-e^𝑥. This simplifies to 𝑥-e^𝑥.

A Function Composed of Itself

A function, f(𝑥) can be composed with itself to form f(f(𝑥)), which can also be written as f²(𝑥). This means that the function is placed as the input to itself. For example if f(𝑥)=5𝑥-2, then in f(f(𝑥)), the 𝑥 in f(𝑥)=5𝑥-2 will be replaced with 5𝑥-2. f(f(𝑥))=5(5𝑥-2)-2, which simplifies to 25𝑥-12.

The Domain of Composite Functions

To calculate the domain of a composite function gf(𝑥):

1. Find the values that are excluded from the domain of the outer function, g(𝑥).
2. Set f(𝑥) equal to these excluded values and solve for 𝑥 to find the values that must be excluded from the domain.
3. Find any further values that are excluded from the domain of the inner function, f(𝑥).
4. Combine these results to form the overall domain of the composite function.

For example if and , find the domain of .

Step 1. Find the values that are excluded from the domain of g(𝑥)

In the function g(𝑥) , there cannot be a denominator of 0.

x≠0 as we cannot divide by 0.

Step 2. Set f(𝑥) equal to these excluded values and solve for 𝑥

.

We solve this for 𝑥 to find any further values that must be excluded from the domain.

We square both sides of the equation.

We then see that .

Step 3. Find any values that are excluded from the inner function, f(𝑥)

. We cannot square root a negative number.

Therefore .

Step 4. Combine these results to determine the domain of the composite function

In , the domain is that .

However in step 2 we run into problems if because this leads to a denominator of zero in the composite function.

Therefore the final domain of the composite function is .

Composite Functions From Graphs

To find the value of a composite function from a graph:

1. Use the input of the composite function to read the output from the graph of the inner function.
2. Use this output as the input of the graph of the outer function.

For example the functions of f(𝑥) and g(𝑥) are shown below.

Use the graphs to calculate the value of the composite function, g(f(5)).

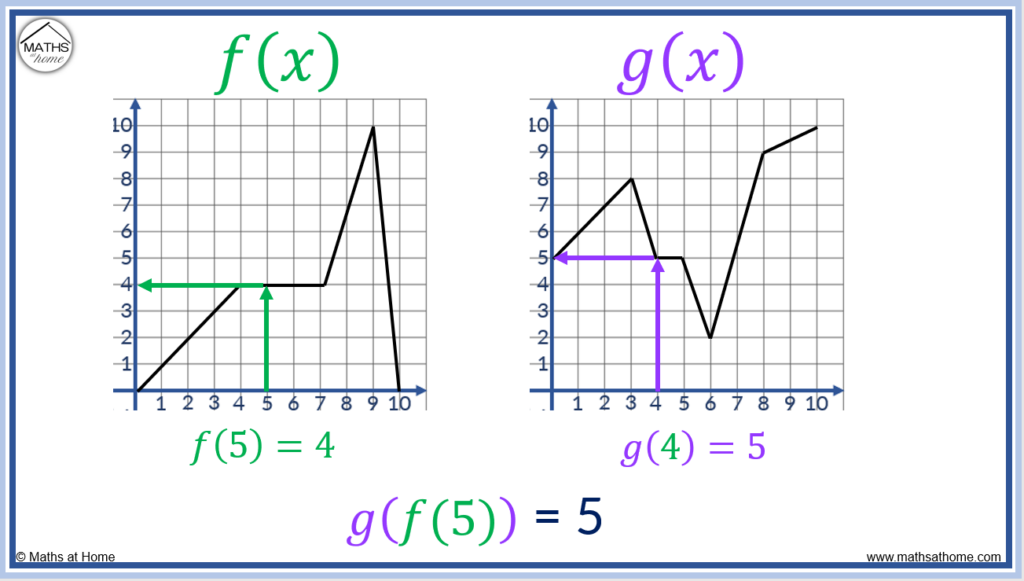
Step 1. Use the input of the composite function to read the output from the graph of the inner function

The number input to the composite function is 5.

We read the graph of the inner function of f(𝑥) at the point where 𝑥 = 5.

When 𝑥 = 5, the f(𝑥) function has an output of 4.

Step 2. Use this output as the input of the graph of the outer function

We use the output of 4 from the first graph as the input to the outer function, g(𝑥).

When 𝑥 = 4, g(𝑥) has an output of 5.

Therefore, g(f(𝑥)) = 5.

Here is another example.

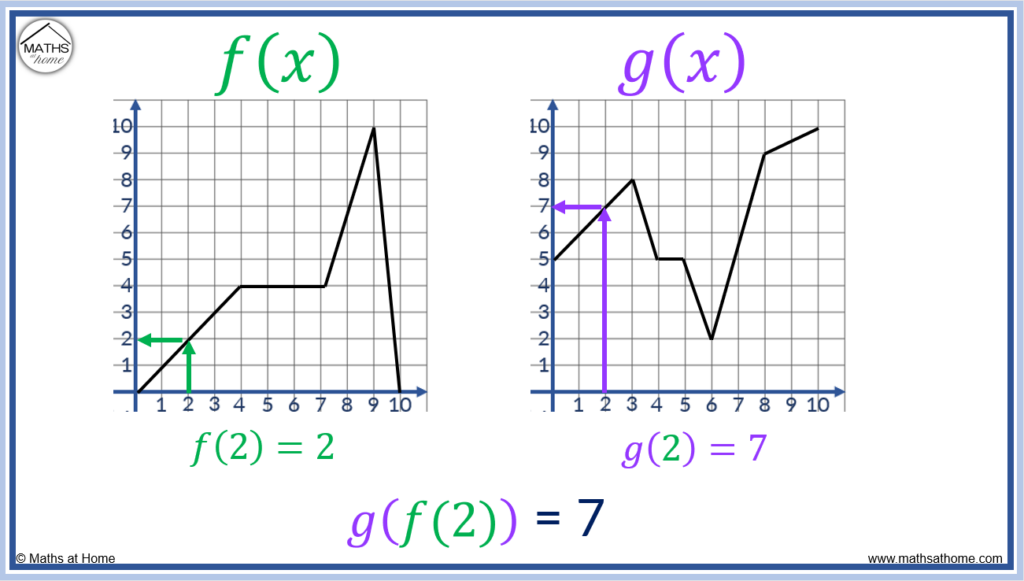
To calculate g(f(2)), we first substitute 2 as an input into the f(𝑥) graph.

This gives us an output of 2 on the y-axis.

We then use this output of 2 from the f(𝑥) graph as an input to the g(𝑥) graph.

When 𝑥 = 2, g(𝑥) has an output of 7.

Therefore g(f(2)) = 7.

Composite Functions Using a Table

To calculate the value of a composite function from a table:

1. Read the output of the inner function from its table at the value required.
2. Use this output as the input in the table of the outer function and read the new output.

For example, calculate the value of the composite function, g(f(3)) using the tables below.

Step 1. Read the output of the inner function from its table at the value required

The input of the composite function is 𝑥 = 3.

From the first table, when 𝑥 = 3 the value of f(𝑥) = 5.

Step 2. Use this output as the input in the table of the outer function and read the new output

The output of the f(𝑥) table was 5.

This is used as the input in the g(𝑥) table.

When 𝑥 = 5, g(𝑥) = 17.

Therefore g(f(3)) = 17.