Completing the Square Video Lesson
How to Complete the Square
To complete the square for 𝑥2+b𝑥+c:
- Divide b by 2 and write this inside brackets squared as (𝑥 + b/2)2
- Square the value of b/2 and subtract it.
- Add the constant term of c to this result.
- The final result is given by (𝑥 + b/2)2 + c – (b/2)2.
For example, complete the square for y = 𝑥2 + 4𝑥 + 1.

Step 1. Divide the coefficient of 𝑥 by 2
The coefficient of 𝑥 is 4.
4 ÷ 2 = 2 and so, we write (𝑥 + 2)2.
This step is shown with a purple arrow.
Step 2. Square the value found in step 1 and subtract it
The value found in step 1 is half of the 𝑥 coefficient. Half of 4 is 2.
We square 2 and subtract this.
22 = 4 and so we subtract 4.
This step is shown with the green arrow.
Step 3. Bring down the constant term
In the equation y = 𝑥2 + 4𝑥 + 1, the constant term is 1.
We add this value to our result.
This step is shown with the red arrow.
Finally, we simplify the constant terms.
-4 + 1 = -3 and so we write this as y = (𝑥 + 2)2 – 3.
Formula for Completing the Square
The formula for completing the square for a quadratic, y = 𝑥2 + b𝑥 + c, is .

If y = 𝑥2 + 6𝑥 + 4, then b = 6 and c = 4.
Therefore b/2 = 3.
Therefore becomes
.
We can simplify 4 – (3)2 to 4 – 9 which equals -5.
The final form of the answer is y = (𝑥 + 3)2 – 5.

Here is an example of completing the square when the value of b is odd.
Complete the square for y = 𝑥2 + 3𝑥 + 3.
When the coefficient of 𝑥 is odd, write it as a fraction over 2 when completing the square.
Step 1. Divide the coefficient of 𝑥 by 2
The coefficient of 𝑥 is 3.
To divide 3 by 2, write this as 3/2.
We write this inside the bracket as (𝑥 + 3/2)2.
This step is written in purple below.
Step 2. Square this value and subtract it
To square 3/2, square the numerator and denominator separately.
32 = 9 and 22 = 4.
We subtract 9/4 from the brackets written in step 1.
This step is written in green below.
Step 3. Bring down the constant term
The constant term of y = 𝑥2 + 3𝑥 + 3 is the number on its own. It is 3.
We add 3 to the equation built so far.
This step is shown in red below.
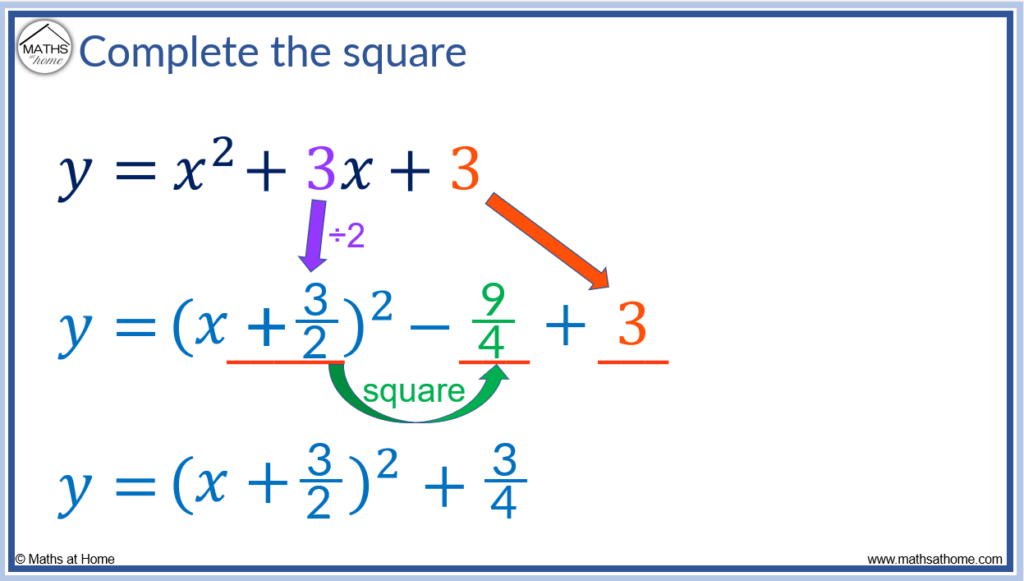
Finally, we simplify by collecting the constant terms of –9/4 and + 3.
3 can be written as 12/4.
–9/4 + 12/4 = 3/4.
Therefore the result is y = (𝑥 + 3/2)2 + 3/4.
What is Completing the Square?
Completing the square is an algebraic method used to rearrange a quadratic equation from y = a𝑥2+b𝑥+c to the form of y = a(𝑥+b)2+c. Completing the square allows us to solve quadratic equations that cannot be factorised and to find the turning point of a quadratic. It is possible to complete the square for any quadratic equation.
For example, completing the square with y = 𝑥2 + 4𝑥 + 1 rearranges the equation to y = (𝑥 + 2)2 – 3.
y = 𝑥2 + 4𝑥 + 1 and y = (𝑥 + 2)2 – 3 are the same equation, just rearranged.

Proof of Completing the Square
Completing the square can be proven algebraically by expanding (𝑥 + b/2)2 to get 𝑥2 + b𝑥 + (b/2)2. This means that any quadratic of the form 𝑥2 + b𝑥 can be rearranged to (𝑥 + b/2)2 – (b/2)2.
Adding a constant term of c to both sides of the equation, any quadratic of the form 𝑥2 + b𝑥 + c can be written as .
Visual Proof of Completing the Square
Completing the square can be shown visually using the following steps.
- Consider a square of area 𝑥2 and a rectangle of area b𝑥.
- Divide the rectangle b𝑥 in half to form two rectangles of area b/2 𝑥.
- Place these two rectangles around the square of 𝑥2
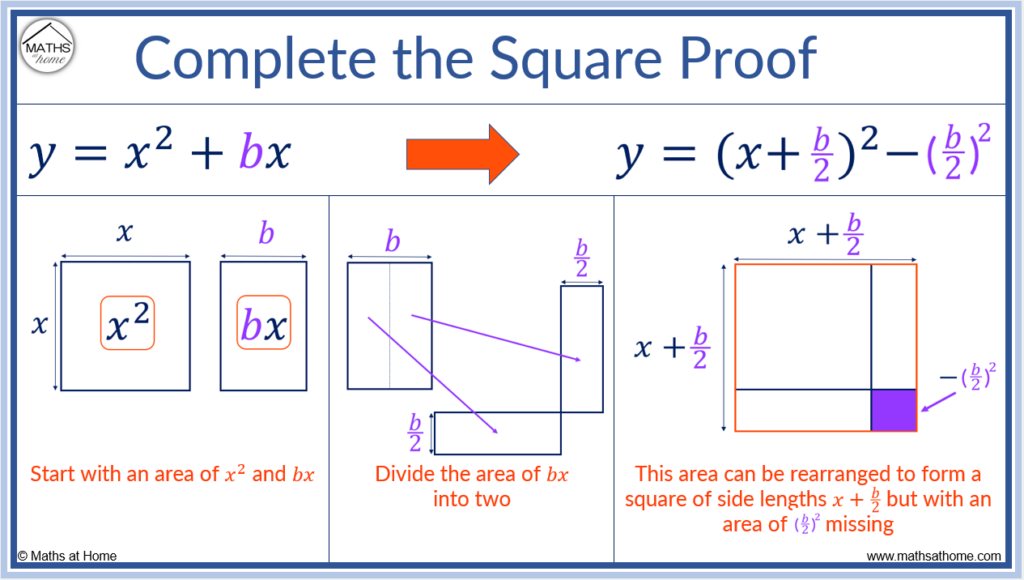
4. The square of 𝑥2 plus the two rectangles almost form a square with side lengths of 𝑥 + b/2. However, there is a small square of side length b/2 missing.
The area of the overall square (outlined in red above) would be (𝑥 + b/2)2.
The area of the purple square above would be (b/2)2.
Therefore (𝑥 + b/2)2 – (b/2)2 = 𝑥2 + b𝑥.
Adding a constant term of c to each side of the equation tells us that .
How to Complete the Square with a Coefficient
To complete the square with a coefficient of 𝑥2:
- Factorise the coefficient
- Complete the square inside the bracket
- Simplify the terms inside the bracket Expand the bracket
For example, complete the square for y = 2𝑥2 + 8𝑥 – 6.
Step 1. Factorise the coefficient
The coefficient of 𝑥2 is 2.
We factorise the expression by bringing a 2 in front of the brackets and dividing every term inside the brackets by 2.
We get y = 2[𝑥2 + 4𝑥 – 3]

Step 2. Complete the square inside the bracket
Inside the bracket of y = 2[𝑥2 + 4𝑥 – 3] is 𝑥2 + 4𝑥 – 3. We complete the square with this.
i) We halve the 𝑥 coefficient of 4 to get 2. Therefore inside the bracket we have (𝑥 + 2)2.
ii) We subtract this value squared. 2 squared is 4 so we get (𝑥 + 2)2 – 4.
iii) We bring the constant term down. The constant term is -3 so we get (𝑥 + 2)2 – 4 – 3.
Step 3. Simplify the terms inside the bracket
We can simplify (𝑥 + 2)2 – 4 – 3 to (𝑥 + 2)2 – 7.
Step 4. Expand the bracket
We have y = 2[ (𝑥 + 2)2 – 7 ].
To expand this, we multiply the (𝑥 + 2)2 term and the -7 term both by 2.
We get y = 2(𝑥 + 2)2 – 14.
Completing the Square with a Negative Coefficient
In this example we will complete the square with a negative coefficient of 𝑥2.
Complete the square for y = -3𝑥2 + 6𝑥 – 9. In this example, the coefficient of 𝑥2 is -3.
Step 1. Factorise the coefficient of 𝑥2
We factorise the coefficient of -3 by writing -3 in front of the brackets and dividing each term within the brackets by -3.
Because we are factorising a negative number, the signs of the terms inside the bracket switch from + to – or – to + respectively.
y = -3𝑥2 + 6𝑥 – 9 becomes y = -3[ 𝑥2 – 2𝑥 + 3 ].

Step 2. Complete the square inside the bracket
Inside the bracket of y = -3[𝑥2 – 2𝑥 + 3] is 𝑥2 – 2𝑥 + 3. We complete the square with this.
i) We halve the 𝑥 coefficient of -2 to get -1. Therefore inside the bracket we have (𝑥 – 1)2.
ii) We subtract this value squared. (-1) squared is 1 so we get (𝑥 – 1)2 – 1.
iii) We bring the constant term down. The constant term is 3 so we get (𝑥 – 1)2 – 1 + 3.
Step 3. Simplify terms inside the bracket
Inside the bracket, (𝑥 – 1)2 – 1 + 3 can be simplified to (𝑥 – 1)2 + 2.
Step 4. Expand the bracket
We have y = -3[ (𝑥 – 1)2 + 2 ].
To expand this, we multiply the (𝑥 – 1)2 term and the +2 term both by -3.
We get y = -3(𝑥 – 1)2 – 6.
How to Solve an Equation by Completing the Square
Any quadratic equation can be solved by completing the square. After completing the square, move the constant terms so that they are on a different side of the equation to the squared brackets to get (𝑥 + a)2 = k. Then square root both sides to get 𝑥 + a = ±√k. Subtracting a from both sides gives the solution as 𝑥 = -a ±√k.
For example, solve the equation 𝑥2 + 8𝑥 + 5 = 0.
Step 1. Complete the square
i) Halve the coefficient of 𝑥.
The coefficient of 𝑥 is 8 and half of 8 is 4. We start with writing (𝑥 + 4)2.
ii) Square this value and subtract it
4 squared is 16, so we subtract 16 to get (𝑥 + 4)2 – 16
iii) Bring down the constant term.
The constant term of 𝑥2 + 8𝑥 + 5 is 5, so we add 5 to get (𝑥 + 4)2 – 16 + 5.
This simplifies to (𝑥 + 4)2 – 11.

Step 2. Solve for 𝑥
i) First separate the squared brackets and any constant terms on either side of the equals sign
We add 11 to both sides so that (𝑥 + 4)2 is on the left of the equals sign and 11 is on the right of it.
ii) Square root both sides of the equation
The square root of (𝑥 + 4)2 is just 𝑥 + 4.
The square root of 11 is ±√11. We need to remember to take both the positive an negative solutions.
iii) Solve for 𝑥
We have 𝑥 + 4 = ±√11.
We subtract 4 from both sides to get 𝑥 = -4 ±√11.
Here is another example of solving a quadratic equation by completing the square.
For example, solve the equation 𝑥2 + 6𝑥 – 1 = 0.

Step 1. Complete the square
i) Halve the coefficient of 𝑥.
The coefficient of 𝑥 is 6 and half of 6 is 3. We start with writing (𝑥 + 3)2.
ii) Square this value and subtract it
3 squared is 9, so we subtract 9 to get (𝑥 + 3)2 – 9
iii) Bring down the constant term.
The constant term of 𝑥2 + 6𝑥 – 1 is -1, so we subtract 1 to get (𝑥 + 3)2 – 10.
Step 2. Solve for 𝑥
i) First separate the squared brackets and any constant terms on either side of the equals sign
We add 10 to both sides so that (𝑥 + 3)2 is on the left of the equals sign and 10 is on the right of it.
ii) Square root both sides of the equation
The square root of (𝑥 + 3)2 is just 𝑥 + 3.
The square root of 10 is ±√10. We need to remember to take both the positive an negative solutions.
iii) Solve for 𝑥
We have 𝑥 + 3 = ±√10.
We subtract 3 from both sides to get 𝑥 = -3 ±√10.
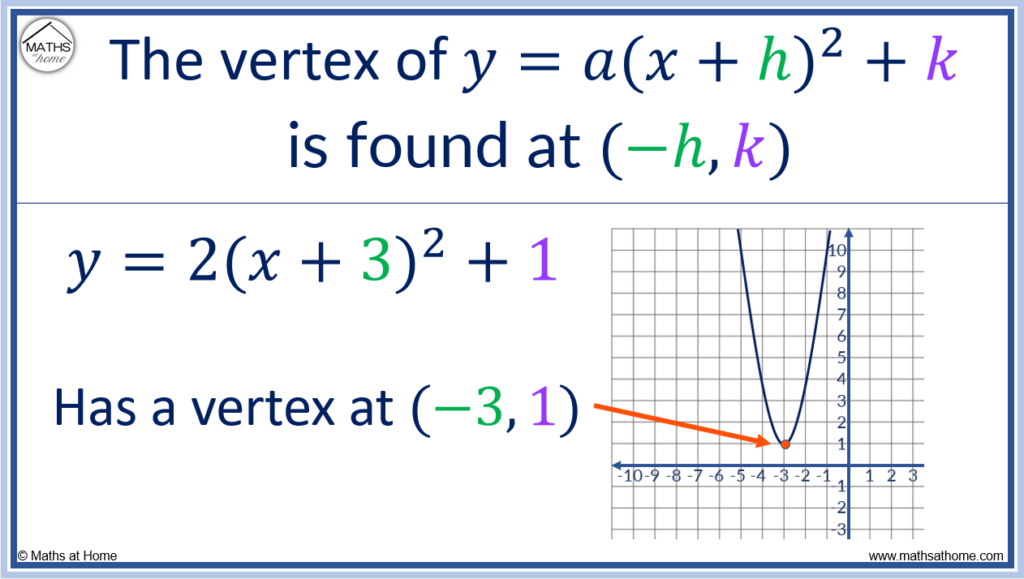
Finding the Vertex by Completing the Square
Completing the square allows a quadratic to be written in the form y = a(𝑥 + h)2 + k. The vertex of the parabola is found at the coordinate (-h, k). For example, the parabola y = 2(𝑥 + 3)2 + 1 has a vertex at the coordinate (-3, 1).
The vertex is the turning point of a parabola.
The graph below shows the vertex of y = 2(𝑥 + 3)2 + 1 at (-3, 1).
The vertex is found at the 𝑥 value that causes the brackets to be equal to zero.
In the equation y = 2(𝑥 + 3)2 + 1, the brackets are squared.
When we square a value, the result is always positive. Therefore the bracket squared can never be negative.
This means that the smallest value that can be output by the equation y = 2(𝑥 + 3)2 + 1 is when the bracket is worth zero.
The value of 𝑥 that causes this to happen is at 𝑥 = -3.
When 𝑥 = -3, the equation of y = 2(𝑥 + 3)2 + 1 becomes y = 1.
Therefore we find the minimum value at 𝑥 = -3, y = 1 or written as a coordinate (-3, 1).
Here is an example of finding the vertex of a quadratic by completing the square.
For example, find the vertex of y = 𝑥2 – 2𝑥 + 3
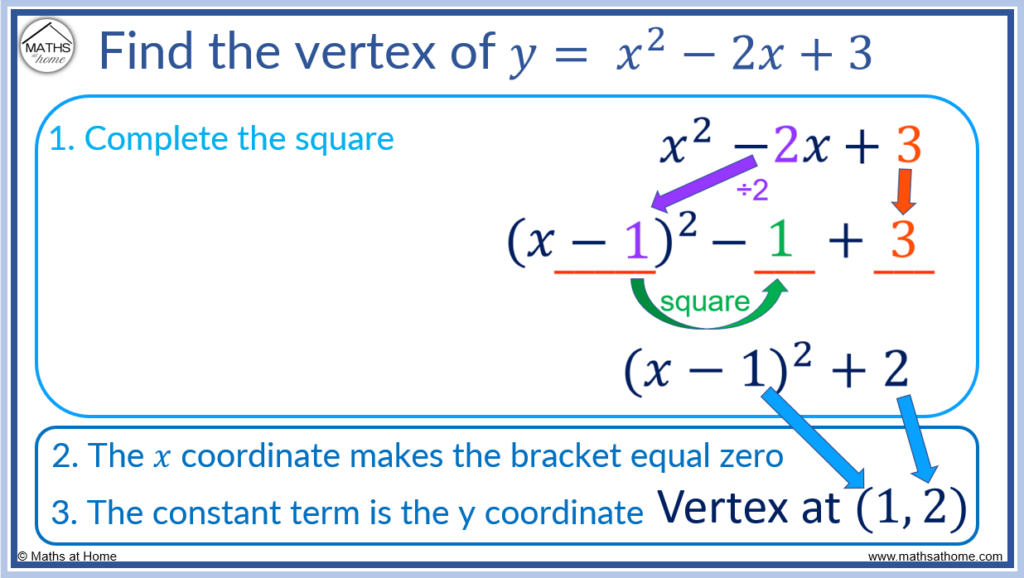
Step 1. Complete the square
i) Halve the coefficient of 𝑥.
The coefficient of 𝑥 is -2 and half of -2 is -1. We start with writing (𝑥 – 1)2.
ii) Square this value and subtract it
(-1) squared is 1, so we subtract 1 to get (𝑥 – 1)2 – 1
iii) Bring down the constant term.
The constant term of 𝑥2 – 2𝑥 + 3 is 3, so we add 3 to get (𝑥 – 1)2 + 2.
Step 2. Read the vertex from the complete the square form
The 𝑥 coordinate of the vertex is the value of 𝑥 that makes the bracket equal to zero.
In y = (𝑥 – 1)2 + 2, the expression inside the bracket is 𝑥 – 1.
This is equal to zero when 𝑥 = 1. Therefore the 𝑥 coordinate of the vertex is at 𝑥 = 1.
The y coordinate of the vertex is simply the constant term in y = (𝑥 – 1)2 + 2. This is just the +2 at the end.
The y coordinate of the vertex is at y = 2.
Therefore the coordinate of the vertex is at (-1 , 2).
Notice how the value of the 𝑥 coordinate is opposite sign to the sign written in the brackets but the y coordinate is the same sign as the constant term at the end.
Here are some examples of reading the turning point from an equation in complete the square form.
| Equation | Coordinates of the Vertex |
| y = a(𝑥 + h)2 + k | (-h, k) |
| y = (𝑥 + 3)2 + 5 | (-3, 5) |
| y = 5(𝑥 + 1)2 + 2 | (-1, 2) |
| y = (𝑥 – 3)2 + 7 | (3, 7) |
| y = 2(𝑥 – 4)2 – 3 | (4, -3) |
| y = 0.1(𝑥 + 2)2 – 6 | (-2, -6) |
| y = (𝑥 – 5)2 | (5, 0) |
