How to Find the Angle Between Two Vectors: Video Lesson
Angle Between Two Vectors Calculator
The calculator below calculates the angle between 2D and 3D vectors. Simply enter the components of each vector in the form
How to Find the Angle Between Two Vectors
To find the angle between two vectors:
- Find the dot product of the two vectors.
- Divide this by the magnitude of the first vector.
- Divide this by the magnitude of the second vector.
- Take the inverse cosine of this value to obtain the angle.
For example, find the angle between and
.
Step 1. Find the dot product of the two vectors
To find the dot product of two vectors, multiply the corresponding components together and add them up.
The dot product of two 2D vectors and
is found using
.
For vectors and
, the dot product
.
Therefore

Step 2. Divide this by the magnitude of the first vector
To calculate the magnitude of a vector, use Pythagoras’ Theorem with the 𝑥 and y components of the vector.
The magnitude of any vector is found as follows: .
The magnitude of the vector is hence
.
This becomes which is
.
The magnitude of the first vector, a is .
We divide the dot product previously calculated by this magnitude.
We get
Step 3. Divide this by the magnitude of the second vector
The magnitude of the second vector, b is found with .
For the vector , the magnitude is
.
This becomes which is
.
We divide the previous result by this magnitude to get
Step 4. Take the inverse cosine of this result
The formula to find the angle between two vectors is .
This can be rearranged for by taking the inverse of cosine on both sides of the equation.
The angle between two vectors is .
As previously calculated:
Using a calculator we enter, .
This gives us the angle between the two vectors as .
Angle Between Two Vectors Formula
The formula for the angle between two vectors, a and b is θ=cos-1( a•b/|a||b|). Where vector a is (ax ay) and vector b is (bx by), the dot product a•b=ax bx+ ay by. The magnitude of the vector |a|=√(ax2+ay2) and the magnitude of the vector |b|=√(bx2+by2).
The most common display of the formula for the angle between two vectors is shown below as .

This formula can be rearranged into a more practical formula by taking the inverse cosine of both sides of the equation.
This gives us a direct formula for the angle between two vectors.
The angle between two vectors is .

We can use this formula to find the angle between the two vectors in 2D.
Find the angle between the vectors and
.
In these two vectors, ax = 2, ay = 5, bx = -4 and by = -1.
The dot product is found using , which for our vectors becomes
and so
.
The magnitude of each vector is found using Pythagoras’ theorem with the 𝑥 and y components.
For these vectors, and so
.
and so
.
The formula can now be used.
and this can be evaluated directly on the calculator to give
.

How to Find the Angle Between Two Vectors in 3D
To find the angle between two vectors in 3D:
- Find the dot product of the vectors.
- Divide the dot product by the magnitude of each vector.
- Use the inverse of cosine on this result.
For example, find the angle between and
.
These vectors contain components in 3 dimensions, 𝑥, y and z.
For the vector , ax =2, ay = -1 and az = 3.
For the vector , bx =2, by = 0 and bz = 1.
Step 1. Find the dot product of the vectors
To find the dot product of two vectors, multiply the corresponding components of each vector and add the results.
For a vector in 3D, .
For our vectors, this becomes .
This becomes which simplifies to
.

Step 2. Divide this dot product by the magnitude of the two vectors
To find the magnitude of a vector in 3D, use Pythagoras’ theorem. For example, .
For the vector ,
. This simplifies to
.
For the vector ,
. This simplifies to
.
We divide the dot product found in step 1 by both of these magnitudes.
We get .
Step 4. Use the inverse of cosine on this result
The formula for the angle between two vectors is . This formula can be used for vectors in 2D or 3D.
To rearrange this formula for the angle, we take the inverse cosine of both sides.
We previously calculated ,
and
.
Therefore .
This can be evaluated on the calculator to give the angle between the two vectors as .
What does the sign of cosθ tell us about the vectors?
If the value of cosθ is positive, the angle between the vectors is acute. If the value of cosθ is negative, the angle between the vectors is obtuse.
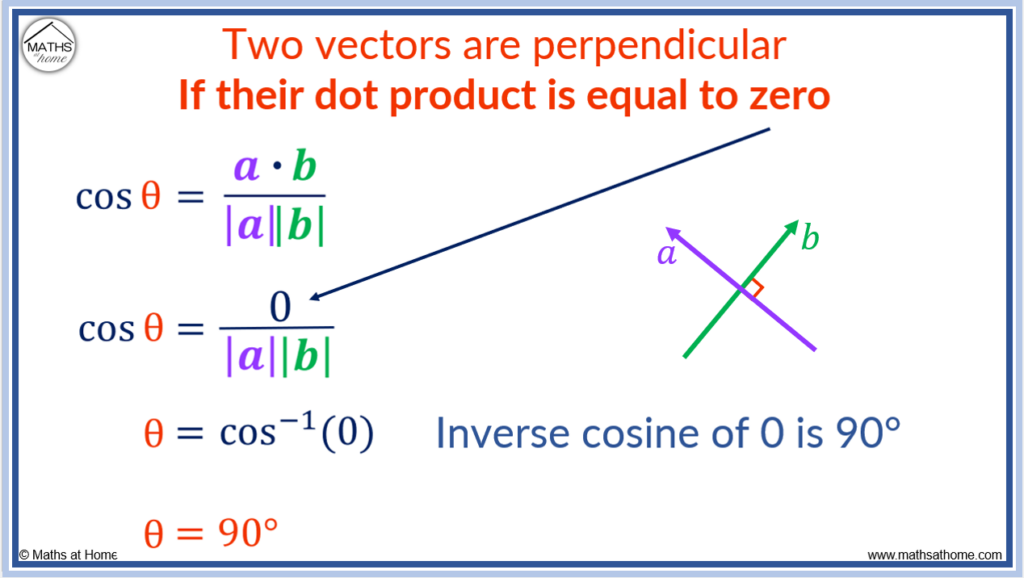
How to Decide if Two Vectors are Perpendicular
Two vectors are perpendicular if their dot product is equal to zero. For two vectors (ax ay) and (bx by), the dot product is given by a•b = ax bx + ay by. If ax bx+ ay by = 0, the two vectors are perpendicular. This means that they meet at right angles.
The formula for the angle between two vectors is given by .
If , then this formula becomes
.
If the numerator of a fraction is zero, then the whole fraction is worth zero. Therefore the formula becomes .
Solving this for the angle we use the inverse cosine of zero, .
The inverse cosine of zero is 90°.
Therefore if the dot product of two vectors is zero, the angle between the two vectors will always result in 90°.
For example, show that and
are perpendicular.
If two vectors are perpendicular, this means that they meet at right angles.
To show that two vectors are perpendicular, calculate the dot product. If the dot product of the two vectors is zero, the vectors are perpendicular.
If the dot product is any other number other than zero, the vectors are not perpendicular.

The dot product is found using .
In the vectors and
, ax = 3, ay = 4, bx = -8 and by = 6.
Therefore the dot product becomes .
Evaluating this we get and so,
.
The dot product is zero and so, the vectors are perpendicular.
