How to Find the Inverse of a 2×2 Matrix

Video Lesson: How to Find the Inverse of a 2×2 Matrix

What is the Inverse of a Matrix?

The inverse of a matrix is another matrix that when multiplied by the original matrix results in the identity matrix. For any given matrix, A, its inverse is denoted as A-1. Therefore AA-1=I and A-1A=I.

It is possible to add, subtract and multiply matrices but not divide them.

Instead, to ‘divide’ by a matrix, we multiply by its inverse.

Multiplying a matrix by its own inverse matrix results in the identity matrix. The identity matrix is the matrix equivalent of the number 1. The identify matrix is a square matrix containing all zeros except for the leading diagonal (top-left to bottom-right) which contains only the number 1.

a matrix multiplied by its inverse results in the identity matrix

For example, the matrix A equals the 2 by 2 matrix Row 1: 4 3 Row 2: 3 2 has an inverse matrix of A to the negative 1 power equals the 2 by 2 matrix Row 1: negative 2 3 Row 2: 3 negative 4.

When the two matrices are multiplied together, the result is the identity matrix, the 2 by 2 matrix Row 1: 4 3 Row 2: 3 2 times the 2 by 2 matrix Row 1: negative 2 3 Row 2: 3 negative 4 equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1.

multiply a matrix by its inverse to obtain the identity matrix

Multiplying a matrix by its reciprocal is like multiplying a normal integer by its reciprocal.

For example, multiplying the number 5 by its reciprocal of 1/5 results in one. 5 times one fifth equals 1.

The identity matrix is the matrix equivalent of the number 1.

How to Find the Inverse of a 2×2 Matrix

To find the inverse of a 2×2 matrix, swap the numbers on the top-left to bottom-right diagonal with each other, change the signs of the numbers on the top-right to bottom-left diagonal and then divide all numbers by the determinant (ab-bd).

For any 2×2 matrix: A equals the 2 by 2 matrix Row 1: a b Row 2: c d, its inverse is given by the formula:

A to the negative 1 power equals the fraction with numerator 1 and denominator a d minus b c times the 2 by 2 matrix Row 1: d negative b Row 2: negative c a

Formula for the inverse of a 2×2 matrix, where a d minus b c is not equal to 0

The value of a d minus b c is known as the determinant of the matrix.

formula for the inverse of a 2x2 matrix

For example, calculate the 2×2 inverse matrix of the matrix A equals the 2 by 2 matrix Row 1: 2 1 Row 2: 4 5.

Comparing this matrix to A equals the 2 by 2 matrix Row 1: a b Row 2: c d, we can see that:

  • a = 2
  • b = 1
  • c = 4
  • d = 5

Therefore, the formula of A to the negative 1 power equals the fraction with numerator 1 and denominator a d minus b c times the 2 by 2 matrix Row 1: d negative b Row 2: negative c a becomes:

A to the negative 1 power equals the fraction with numerator 1 and denominator open paren 2 times 5 close paren minus open paren 1 times 4 close paren times the 2 by 2 matrix Row 1: 5 negative 1 Row 2: negative 4 2.

Notice that inside the matrix, the 5 and the 2 on the leading diagonal swapped places and the 1 and the 4 on the non-leading diagonal became -1 and -4.

Evaluating the determinant on the bottom of the fraction: open paren 2 times 5 close paren minus open paren 1 times 4 close paren equals 6.

Therefore, the inverse matrix becomes: A to the negative 1 power equals one sixth times the 2 by 2 matrix Row 1: 5 negative 1 Row 2: negative 4 2.

This can be simplified by multiplying all elements within the matrix by one sixth to obtain: A to the negative 1 power equals the 2 by 2 matrix Row 1: five sixths negative one sixth Row 2: negative two thirds one third.

example of how to find the inverse of a 2x2 matrix

Here is an alternative method to find the matrix inverse.

The steps to calculate the inverse of a 2×2 matrix are:

  1. Calculate the adjoint by switching the elements on the leading diagonal and changing the sign of the elements on the non-leading diagonal.
  2. Calculate the determinant by subtracting the product of the non-leading diagonal from the product of the leading diagonal.
  3. Divide the adjoint of the matrix by its determinant.

For example, find the inverse matrix of A equals the 2 by 2 matrix Row 1: 1 negative 2 Row 2: negative one half three halves.

Step 1. Calculate the adjoint by switching the elements on the leading diagonal and changing the sign of the elements on the non-leading diagonal

The adjoint of matrix A is found by switching the elements on the leading diagonal (top left to bottom right) and then changing the sign of the elements on the non-leading diagonal.

The elements on the leading diagonal are 1 and 3/2. We switch their positions with each other.

The elements on the non-leading diagonal are -2 and –1/2. They are both negative and so when their signs are changed, they become 2 and 1/2.

Therefore the adjoint of A is: a d j of A equals the 2 by 2 matrix Row 1: three halves 2 Row 2: one half 1.

Step 2. Calculate the determinant by subtracting the product of the non-leading diagonal from the product of the leading diagonal

The leading diagonal elements are 1 and 3/2. Finding their product means to multiply them together so we get 1 times three halves equals three halves.

The non-leading diagonal elements are -2 and –1/2. Their product is negative 2 times negative one half equals 1.

We subtract the product of the non-leading diagonal from the product of the leading diagonal to obtain: three halves minus 1 equals one half.

Therefore, the determinant is equal to one half.

Step 3. Divide the adjoint of the matrix by its determinant

The inverse of the matrix is equal to the adjoint matrix, a d j of A equals the 2 by 2 matrix Row 1: three halves 2 Row 2: one half 1 ,divided by the determinant, one half.

A to the negative 1 power equals the 2 by 2 matrix Row 1: three halves 2 Row 2: one half 1 divided by one half.

This results in each of the elements inside the adjoint matrix doubling in size to obtain:

A to the negative 1 power equals the 2 by 2 matrix Row 1: 3 4 Row 2: 1 2.

example of inverse matrix

Formula for the Inverse of a 2×2 Matrix

For any 2×2 matrix A = [a, b | c, d], the formula for the inverse matrix is A-1 = [1÷(ad-bc)]× [d, -b | -c, a].

A to the negative 1 power equals the fraction with numerator 1 and denominator a d minus b c times the 2 by 2 matrix Row 1: d negative b Row 2: negative c a

Formula for the inverse of a 2×2 matrix, where a d minus b c is not equal to 0

formula for the inverse of a 2x2 matrix

Since a d minus b c is known as the determinant of the matrix, the formula for the 2×2 inverse matrix can be written as:

A to the negative 1 power equals 1 over determinant A times the 2 by 2 matrix Row 1: a b Row 2: c d

Formula for the inverse of a 2×2 matrix

Alternatively, the formula can be written as:

A to the negative 1 power equals 1 over determinant A a d j of A

Formula for the inverse of a 2×2 matrix
formula for the inverse of a matrix using a determinant

The easiest shortcut for calculating the inverse of a 2×2 matrix is A-1 = [ 1 ÷ ( ad – bc ) ] × [d, -b, -c, a].

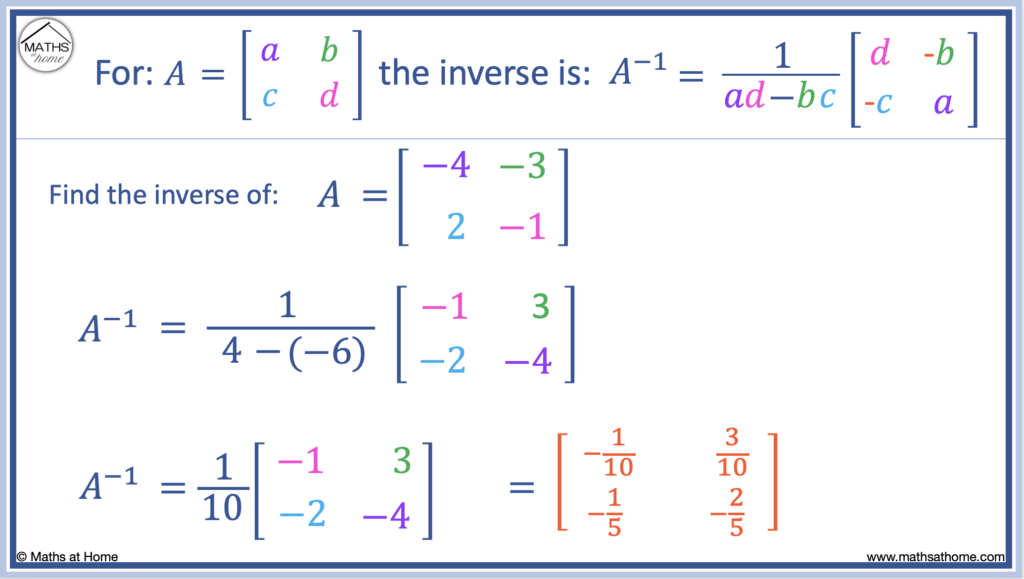
For example, find the inverse of A equals the 2 by 2 matrix Row 1: negative 4 negative 3 Row 2: 2 negative 1.

In this case:

a = -4, b = -3, c = 2 and d = -1.

We substitute into the formula: A-1 = [1÷(ad-bc)]× [d, -b, -c, a] to obtain:

A-1 = [ 1 ÷ ( (-4×-1)-(-3×2) ) ]× [-1, 3, -2, -4].

This can be evaluated as: A-1 = [ 1 ÷ 10 ]× [-1, 3, -2, -4].

We can write the inverse matrix as: A to the negative 1 power equals one tenth times the 2 by 2 matrix Row 1: negative 1 3 Row 2: negative 2 negative 4.

Multiplying each element in the matrix by 1/10 (or by dividing them by 10), we obtain:

A to the negative 1 power equals the 2 by 2 matrix Row 1: negative one tenth three tenths Row 2: negative one fifth negative two fifths.

how to find the inverse of a 2x2 matrix using the formula

Matrices with No Inverse

A matrix does not have an inverse if it has a determinant equal to zero. A matrix that does not have an inverse is called non-invertible or singular.

For a matrix to have an inverse:

  • It must be a square matrix.
  • Its determinant must not be equal to zero.

A non-square matrix is a matrix in which the number of columns is not equal to the number of rows. Only square matrices, in which the number of columns is equal to the number of rows, have inverses. Non-square matrices do not have an inverse.

For any 2×2 matrix of the form A equals the 2 by 2 matrix Row 1: a b Row 2: c d, it does not have an inverse if a d minus b c equals 0.

That is because the formula for the inverse is A to the negative 1 power equals 1 over determinant A times the 2 by 2 matrix Row 1: a b Row 2: c d and we cannot have 0 on the denominator of a fraction because it would result in dividing by zero.

For example, find the inverse of A equals the 2 by 2 matrix Row 1: 4 2 Row 2: 6 3.

The determinant is equal to (4×3) – (2×6) which equals 12 – 12 = 0.

This matrix has no inverse.

2x2 matrix with no inverse

For a matrix to have an inverse, it must be a 1:1 matrix and one row must not be a multiple of another row.

In the example above, we can see that the bottom row of [6 3] is 1.5 times the top row [4 2].

Another example of a matrix that has no inverse is A equals the 2 by 2 matrix Row 1: 1 1 Row 2: 2 2.

We can see that the bottom row is twice as large as the top row.

We will call the proposed inverse of this matrix B, whereB equals the 2 by 2 matrix Row 1: a b Row 2: c d.

Any matrix multiplied by its inverse will result in the identity matrix, I equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1.

Therefore, A B equals I and therefore, the 2 by 2 matrix Row 1: 1 1 Row 2: 2 2 times the 2 by 2 matrix Row 1: a b Row 2: c d equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1.

Multiplying the matrices out, we see that a plus c equals 1 and 2 a plus 2 c equals 0.

This results in a contradiction, since there is no solution for which both of these statements are true.

This means that B cannot be the inverse of A and therefore, A cannot have an inverse.

Self-Inverse Matrices

A self-inverse matrix is a matrix that is identical to its inverse matrix. That is, A2 = I. A matrix that is its own inverse is called involutory.

An example of a self-inverse matrix is the 2 by 2 matrix Row 1: 2 3 Row 2: negative 1 negative 2.

the 2 by 2 matrix Row 1: 2 3 Row 2: negative 1 negative 2 times the 2 by 2 matrix Row 1: 2 3 Row 2: negative 1 negative 2 equals the 2 by 2 matrix Row 1: Column 1, open paren 2 times 2 close paren plus open paren 3 times negative 1 close paren Column 2, open paren 2 times 3 close paren plus open paren 3 times negative 2 close paren Row 2: Column 1, open paren negative 1 times 2 close paren plus open paren negative 2 times negative 1 close paren Column 2, open paren negative 1 times 3 close paren plus open paren negative 2 times negative 2 close paren equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1

Therefore we say that if A equals the 2 by 2 matrix Row 1: 2 3 Row 2: negative 1 negative 2, then A to the negative 1 power equals the 2 by 2 matrix Row 1: 2 3 Row 2: negative 1 negative 2.

The identity matrix is a self-inverse matrix since II=I. The identity matrix multiplied by itself produces the identity matrix.

the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 times the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1.

We say that I to the negative 1 power equals I.

Inverse of a 2×2 Matrix Using Elementary Row Operations

To find the inverse of a 2×2 matrix, A, using row operations, first write the matrix as A=IA, where I is the identity matrix. Then apply a sequence of row operations to obtain the form I=BA, where B is the inverse matrix.

When performing row operations, we can subtract multiples of a row from another and we can multiply an entire row by a number.

The aim to to turn the first matrix into the identity matrix.

For example, find the inverse of A equals the 2 by 2 matrix Row 1: 1 2 Row 2: 3 4.

Here, row 1 (R1) = [1 2] and row 2 (R2) = [3 4].

  1. We first write the equation in the form A=IA like so: the 2 by 2 matrix Row 1: 1 2 Row 2: 3 4 equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 times A.
  2. Now we do row operations so that the matrix before the equals sign becomes an identity matrix.

We first do the row operation: R2 = R2 – 3R1 to obtain the 2 by 2 matrix Row 1: 1 2 Row 2: 0 negative 2 equals the 2 by 2 matrix Row 1: 1 0 Row 2: negative 3 1 times A.

Now we do the row operation: R2 = negative one halfR2 to obtain the 2 by 2 matrix Row 1: 1 2 Row 2: 0 1 equals the 2 by 2 matrix Row 1: 1 0 Row 2: three halves negative one half times A.

Finally, we do the row operation: R1 = R1 – 2R2 to obtain the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 equals the 2 by 2 matrix Row 1: negative 2 1 Row 2: three halves negative one half times A.

Now that the row reduction is complete, the inverse matrix is found just after the equals sign.

Therefore A to the negative 1 power equals the 2 by 2 matrix Row 1: negative 2 1 Row 2: three halves negative one half.

Here is another example.

Find the inverse of A equals the 2 by 2 matrix Row 1: 3 2 Row 2: negative 7 negative 5.

  1. We first write the matrix equation as the 2 by 2 matrix Row 1: 3 2 Row 2: negative 7 negative 5 equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 times A.
  2. Now we do row operations so that the matrix before the equals sign becomes an identity matrix.

First we do: R1 = one third R1 so that: the 2 by 2 matrix Row 1: 1 two thirds Row 2: negative 7 negative 5 equals the 2 by 2 matrix Row 1: one third 0 Row 2: 0 1 times A.

Now R2 = R2 + 7R1, so that: the 2 by 2 matrix Row 1: 1 two thirds Row 2: 0 negative one third equals the 2 by 2 matrix Row 1: one third 0 Row 2: seven thirds 1 times A.

Now R2 = -3R2, so that: the 2 by 2 matrix Row 1: 1 two thirds Row 2: 0 1 equals the 2 by 2 matrix Row 1: one third 0 Row 2: negative 7 negative 3 times A.

Now R1 = R1 – two thirdsR2, so that: the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1 equals the 2 by 2 matrix Row 1: 5 2 Row 2: negative 7 negative 3 times A.

Therefore, the inverse matrix is A to the negative 1 power equals the 2 by 2 matrix Row 1: 5 2 Row 2: negative 7 negative 3.

Proof of the Inverse of a 2×2 Matrix

The general formula for the inverse of a 2×2 matrix can be derived by writing AA-1 = I and then solving the resulting set of equations.

For example, we will call our matrix A equals the 2 by 2 matrix Row 1: a b Row 2: c d.

We will call the proposed inverse matrix A to the negative 1 power equals the 2 by 2 matrix Row 1: w x Row 2: y z

Since any matrix multiplied by its inverse is the identity matrix, we obtain: the 2 by 2 matrix Row 1: a b Row 2: c d times the 2 by 2 matrix Row 1: w x Row 2: y z equals the 2 by 2 matrix Row 1: 1 0 Row 2: 0 1.

Multiplying out, we obtain the following equations:

Equation 1: a w plus b y equals 1

Equation 2: a x plus b z equals 0

Equation 3: c w plus d y equals 0

Equation 4: c x plus d z equals 1

Multiplying Equation 1 by d, we obtain a d w plus b d y equals d.

Multiplying Equation 3 by -b, we obtain negative b c w minus b d y equals 0.

Adding these results, we obtain a d w minus b c w equals d.

We can rearrange this to obtain w times open paren a d minus b c close paren equals d and therefore, w equals the fraction with numerator d and denominator a d minus b c

Multiplying Equation 2 by -d, we obtain negative a d x minus b d z equals 0.

Multiplying Equation 4 by b, we obtain b c x plus b d z equals b.

Adding these results, we obtain b c x minus a d x equals b.

We can rearrange this to obtain x times open paren b c minus a d close paren equals b and therefore: x equals negative the fraction with numerator b and denominator a d minus b c

Multiplying Equation 1 by c, we obtain a c w plus b c y equals c.

Multiplying Equation 3 by -a, we obtain negative a c w minus a d y equals 0.

Adding these results, we obtain b c y minus a d y equals c.

We can rearrange this to obtain y times open paren b c minus a d close paren equals c and therefore: y equals negative the fraction with numerator c and denominator a d minus b c.

Multiplying Equation 2 by -c, we obtain negative a c x minus b c z equals 0.

Multiplying Equation 4 by a, we obtain a c x plus a d z equals a

Adding these results, we obtain a d z minus b c z equals a.

We can rearrange this to obtain 1 lines Line 1: z times open paren a d minus b c close paren equals a and therefore: 1 lines Line 1: z equals the fraction with numerator a and denominator a d minus b c.

Putting the results for w, x, y and z back into our inverse matrix, A to the negative 1 power equals the 2 by 2 matrix Row 1: w x Row 2: y z, we obtain:

A to the negative 1 power equals the 2 by 2 matrix Row 1: Column 1, the fraction with numerator d and denominator a d minus b c Column 2, the fraction with numerator negative b and denominator a d minus b c Row 2: Column 1, the fraction with numerator negative c and denominator a d minus b c Column 2, the fraction with numerator a and denominator a d minus b c.

We can factor out the the fraction with numerator 1 and denominator a d minus b c to obtain the final derived formula: A to the negative 1 power equals the fraction with numerator 1 and denominator a d minus b c times the 2 by 2 matrix Row 1: d negative b Row 2: negative c a.

How to Find the Inverse of a 2×2 Matrix on a Calculator:

Inverse Matrix on a Ti-84

To find the inverse of Matrix A on the Ti84 Calculator:

  1. Press [2nd], [𝑥-1] to open the ‘matrix’ screen.
  2. Highlight [A] and press [ENTER].
  3. Press [𝑥-1] so that ‘[A]-1 is written.
  4. Press [ENTER] to obtain the inverse matrix.

Inverse Matrix on a Casio fx-CG50

To find the inverse of Matrix A on the Casio fx-CG50 calculator:

  1. Press [shift], [2] to type ‘Mat’.
  2. Press [ALPHA] and select [A] so that ‘MatA’ is written.
  3. Press [^] and type ‘-1’ so that ‘MatA-1 is written.
  4. Press ‘EXE’ to calculate the inverse.

Solving a System of Equations Using an Inverse 2×2 Matrix

To solve a system of equations using an inverse matrix:

  1. Write matrix A containing the coefficients of 𝑥 and y with the values from each equation in a different row.
  2. Write matrix B containing the constant terms from each equation in their corresponding rows.
  3. Calculate the solution matrix as X = A-1B.

For example, solve the simultaneous equations:

2 x plus y equals 5

4 x plus 5 y equals 7

Step 1. Write matrix A containing the coefficients of 𝑥 and y with the values from each equation in a different row.

In the first equation, we have 2𝑥 and 1y. Therefore the coefficients for the top row of the matrix are [2 1].

In the second equation, we have 4𝑥 and 5y. Therefore the coefficients for the bottom row are [4 5].

Therefore, matrix A equals the 2 by 2 matrix Row 1: 2 1 Row 2: 4 5.

Step 2. Write matrix B containing the constant terms from each equation in their corresponding rows.

The constant terms are after the equals sign.

In the top row, we have 5.

In the bottom row we have 7.

Therefore matrix B equals the 2 by 1 column matrix 5 7.

Step 3. Calculate the solution matrix as X = A-1B.

Previously, the equation was written as A X equals B, where:

A equals the 2 by 2 matrix Row 1: 2 1 Row 2: 4 5 B equals the 2 by 1 column matrix 5 7 and X equals the 2 by 1 column matrix x y.

We rearrange A X equals B to the form 1 lines Line 1: X equals A to the negative 1 power B by premultiplying both sides by the inverse of matrix A.

We use 1 lines Line 1: X equals A to the negative 1 power B to obtain the solutions.

Since

A equals the 2 by 2 matrix Row 1: 2 1 Row 2: 4 5, we find the inverse matrix as A to the negative 1 power equals the 2 by 2 matrix Row 1: five sixths negative one sixth Row 2: negative two thirds one third.

Using 1 lines Line 1: X equals A to the negative 1 power B we obtain X equals the 2 by 2 matrix Row 1: five sixths negative one sixth Row 2: negative two thirds one third times the 2 by 1 column matrix 5 7.

Multiplying these two matrices, we get X equals the 2 by 2 matrix Row 1: five sixths negative one sixth Row 2: negative two thirds one third times the 2 by 1 column matrix 5 7 equals the 2 by 1 column matrix 3 negative 1.

The answer is therefore x equals 3 and y equals negative 1.

solving a system of equations using inverse matrices