How to Calculate Scalar and Vector Projections

How to Calculate the Vector Projection: Video Lesson

How to Find the Vector Projection

The formula for the vector projection of a onto b is equal to [a⋅b] / [b⋅b] (b).

proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren

The formula for the vector projection of a right arrow onto b right arrow

In this formula:

  • proj sub b right arrow a right arrow is pronounced as ‘the projection of vector a onto the vector b
  • Each vector is made up of a right arrow equals the 2 by 1 column matrix Row 1: a sub x Row 2: a sub y and b right arrow equals the 2 by 1 column matrix Row 1: b sub x Row 2: b sub yin 2D or a right arrow equals the 3 by 1 column matrix Row 1: a sub x Row 2: a sub y Row 3: a sub z and b right arrow equals the 3 by 1 column matrix Row 1: b sub x Row 2: b sub y Row 3: b sub z in 3D.
  • a right arrow times b right arrow is the dot product, calculated by a right arrow times b right arrow equals a sub x b sub x plus a sub y b sub y in 2D or a right arrow times b right arrow equals a sub x b sub x plus a sub y b sub y plus a sub z b sub z in 3D.
  • Similarly, b right arrow times b right arrow equals b sub x squared plus b sub y squared in 2D and b right arrow times b right arrow equals b sub x squared plus b sub y squared plus b sub z squared in 3D
vector projection formula
To calculate the vector projection of ‘a’ onto ‘b’:

  1. Calculate the dot product of ‘a’ and ‘b’.
  2. Divide this by the dot product of ‘b’ and ‘b’.
  3. Multiply this by the vector ‘b’.

For example, calculate the vector projection of the 2 by 1 column matrix 1 3 on the 2 by 1 column matrix 2 1.

We will use the formula, proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren, where a right arrow equals the 2 by 1 column matrix 1 3 and b right arrow equals the 2 by 1 column matrix 2 1.

We first find the dot product of a right arrow and b right arrow.

The dot product is calculated using a right arrow times b right arrow equals a sub x b sub x plus a sub y b sub y.

Therefore, a right arrow times b right arrow equals open paren 1 times 2 close paren plus open paren 3 times 1 close paren equals 5.

and b right arrow times b right arrow equals open paren 2 times 2 close paren plus open paren 1 times 1 close paren equals 5.

Therefore, the formula of proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren becomes proj sub b right arrow a right arrow equals five fifths times the 2 by 1 column matrix 2 1.

Since 5 divided by 5 equals 1, the vector projection is proj sub b right arrow a right arrow equals the 2 by 1 column matrix 2 1

For example, calculate the vector projection of the vector the 2 by 1 column matrix 3 negative 2 on the 2 by 1 column matrix negative 1 5.

The formula proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren is used with a right arrow equals the 2 by 1 column matrix 3 negative 2 and b right arrow equals the 2 by 1 column matrix negative 1 5,

a right arrow times b right arrow equals open paren 3 times negative 1 close paren plus open paren negative 2 times 5 close paren equals negative 13.

b right arrow times b right arrow equals open paren negative 1 times negative 1 close paren plus open paren 5 times 5 close paren equals 26.

Therefore, the formula of proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren becomes proj sub b right arrow a right arrow equals open paren negative 13 over 26 close paren times the 2 by 1 column matrix negative 1 5.

Since negative 13 divided by 26 equals negative one half, proj sub b right arrow a right arrow equals negative one half times the 2 by 1 column matrix negative 1 5 or proj sub b right arrow a right arrow equals the 2 by 1 column matrix one half negative five halves.

how to calculate the projection vector

How to Calculate a Vector Projection in 3D

Here is an example of calculating a vector projection in 3 dimensions.

The formula for calculating a vector projection in 3D is still proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren.

Calculate the projection of the 3 by 1 column matrix 1 0 3 on the 3 by 1 column matrix 4 2 1.

Here, a right arrow equals the 3 by 1 column matrix 1 0 3 and b right arrow equals the 3 by 1 column matrix 4 2 1.

The dot product of these vectors is calculated by multiplying the 𝑥 components, y components and z components together separately.

a right arrow times b right arrow equals open paren 1 times 4 close paren plus open paren 0 times 2 close paren plus open paren 3 times 1 close paren equals 7

b right arrow times b right arrow equals open paren 4 times 4 close paren plus open paren 2 times 2 close paren plus open paren 1 times 1 close paren equals 21

Therefore, the vector projection equation, proj sub b right arrow a right arrow equals open paren the fraction with numerator a right arrow times b right arrow and denominator b right arrow times b right arrow close paren times open paren b right arrow close paren becomes proj sub b right arrow a right arrow equals open paren 7 over 21 close paren times the 3 by 1 column matrix 4 2 1.

This can be simplified to proj sub b right arrow a right arrow equals one third times the 3 by 1 column matrix 4 2 1 or the 3 by 1 column matrix four thirds two thirds one third.

vector projection in 3D

What is Vector Projection

The vector projection of vector ‘a’ on vector ‘b’ tells us what component of vector ‘a’ acts in the direction of vector ‘b’. The result is a vector. If the vector projection is negative, vector ‘a’ is acting in the opposite direction to vector ‘b’.

A simple way to explain vector projection is to consider the shadow formed when a light is shined at right-angles to the vector being projected on.

  1. Consider two vectors ‘a’ and ‘b’.
  2. Consider a light shining perpendicular to vector ‘b’ from above vector ‘a’.
  3. The vector projection of ‘a’ onto ‘b’ is the shadow formed on ‘b’ from the result of this light.
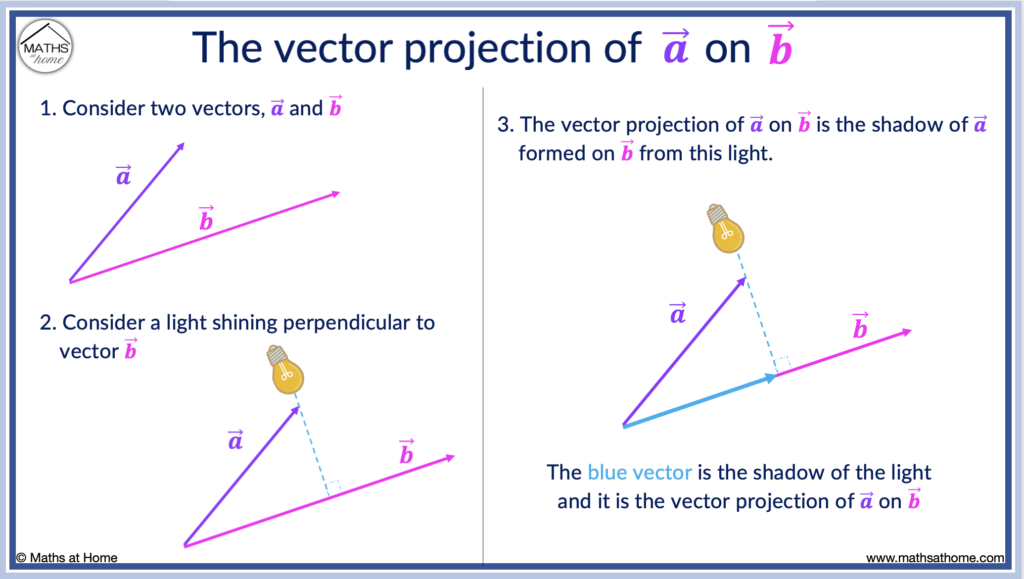
definition of a projection vector explained

The vector projection notation for the projection of vector ‘a’ on vector ‘b’ is proj‘b’ ‘a’.

The notation for the projection of vector a right arrow on vector b right arrow is proj sub b right arrow a right arrow

Similarly the projection vector of vector ‘b’ on vector ‘a’ is proj‘a’ ‘b’.

In general comma the notation for the projection of vector u right arrow onto vector v right arrow is proj sub v right arrow u right arrow

Vector projections are useful in real life applications to better understand how forces applied in different directions can impact motion. For example, the effects of windspeed on aeroplanes or the effect of currents on a boat.

A real life example of vector projection is the case of a box being pulled up a slope by a rope that is inclined at an angle.

In this example, the projection vector of the rope onto the slope tells us how much of this force is used to pull the box in the direction of the slope.

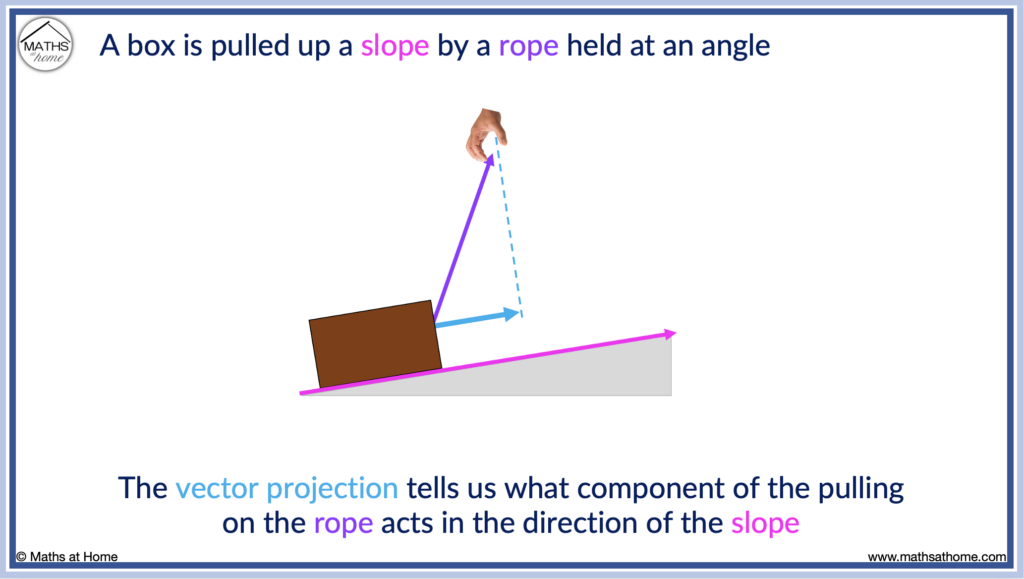
real life example of vector projection

Vector Projection vs Scalar Projection

The vector projection describes the components of a vector that act in the direction of another given vector whereas the scalar projection is the magnitude or length of this vector. The scalar projection is the magnitude of the vector projection.

The vector projection is a vector and provides information about each component of the projection.

The scalar projection is a scalar and simply provides the overall magnitude of the vector but does not tell us the direction it is acting in.

The vector projection can be positive, negative or zero.

  • A positive vector projection means that the vectors are acting in the same direction.
  • A negative vector projection means that the vectors are acting in the opposite direction.
  • A vector projection equal to zero means that the vectors are at right angles.
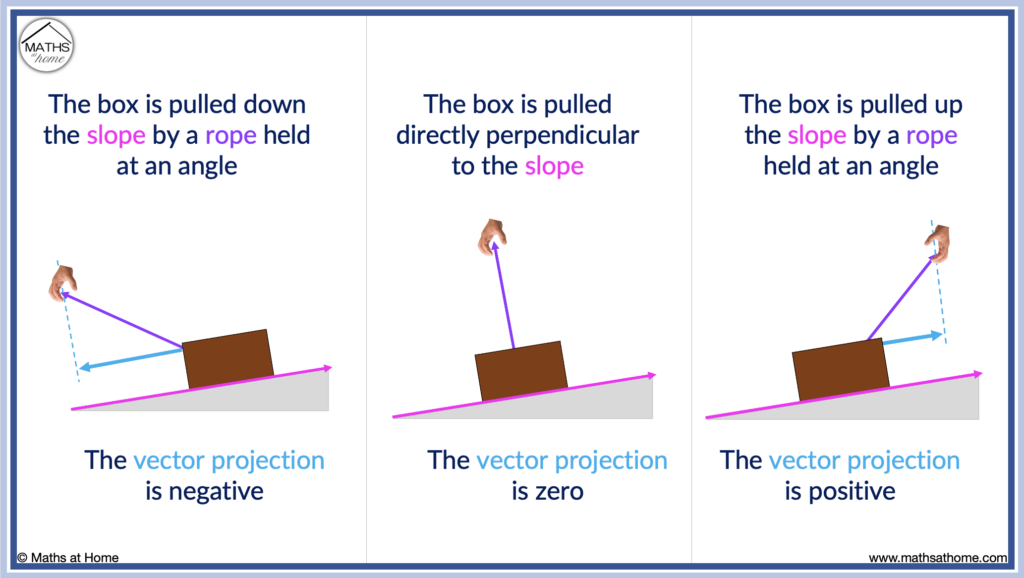
meaning of positive negative and zero projection vectors

In the example of the box above, going up the slope is taken in the positive direction. Therefore when the rope is pulling the box up the slope, the rope is acting in the same direction as the slope and the projection vector is positive. When the rope is pulling the box down the slope, the rope is acting in an opposite direction to the slope and the projection vector is negative.

When the rope is perpendicular to the slope, the rope does not pull the block up or down the slope. Therefore, the projection vector is zero.

The scalar projection is simply the magnitude of the force of the vector. Therefore if the rope is pulled with the same strength in each of the three cases, the scalar projection will be equal in each of these cases.

The scalar projection is the magnitude of the vector projection. To calculate the scalar projection, square the components of the vector projection, add them and then square root. For example, if the vector projection is 3i + 4j, then the scalar projection is √(32 + 42) = 5.

How to Calculate the Scalar Projection

The scalar projection of ‘a’ on ‘b’ is found using |a⋅b| ÷ |b|, where |a⋅b| = a𝑥b𝑥 + ayby and |b| = √(b𝑥2 + by2). For example, the scalar projection of (2, 1) on (3, 4) is (2×3 + 1×4) ÷ √(32 + 42) = 2.

The scalar projection of a right arrow on b right arrow equals the fraction with numerator the absolute value of a right arrow times b right arrow and denominator the absolute value of b right arrow

The formula for calculating the scalar projection
how to calculate the scalar projection

For example, calculate the scalar projection of the vector the 2 by 1 column matrix 4 negative 3 on the vector the 2 by 1 column matrix 2 negative 2.

Since the 2 by 1 column matrix 4 negative 3 is projected onto the 2 by 1 column matrix 2 negative 2, the 2 by 1 column matrix 4 negative 3 is vector a right arrow and the 2 by 1 column matrix 2 negative 2 is vector b right arrow.

The scalar projection equation, s equals the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of b right arrow becomes s equals the fraction with numerator open paren the 2 by 1 column matrix 4 negative 3 times the 2 by 1 column matrix 2 negative 2 close paren and denominator the absolute value of the 2 by 1 column matrix 2 negative 2.

the 2 by 1 column matrix 4 negative 3 times the 2 by 1 column matrix 2 negative 2 equals open paren 4 times 2 close paren plus open paren negative 3 times negative 2 close paren equals 14

the absolute value of b right arrow equals the square root of 2 squared plus open paren negative 2 close paren squared equals the square root of 8.

Therefore the scalar projection is the fraction with numerator 14 and denominator the square root of 8 almost equals 4.95.

example of how to calculate the scalar projection

Scalar Projection: Real Life Example

A box is pulled up a slope by a rope.

The direction vector of the slope is the 2 by 1 column matrix 5 1 and the rope is pulled with a force vector of the 2 by 1 column matrix 8 3N.

Calculate the magnitude of the force acting in the direction of the slope.

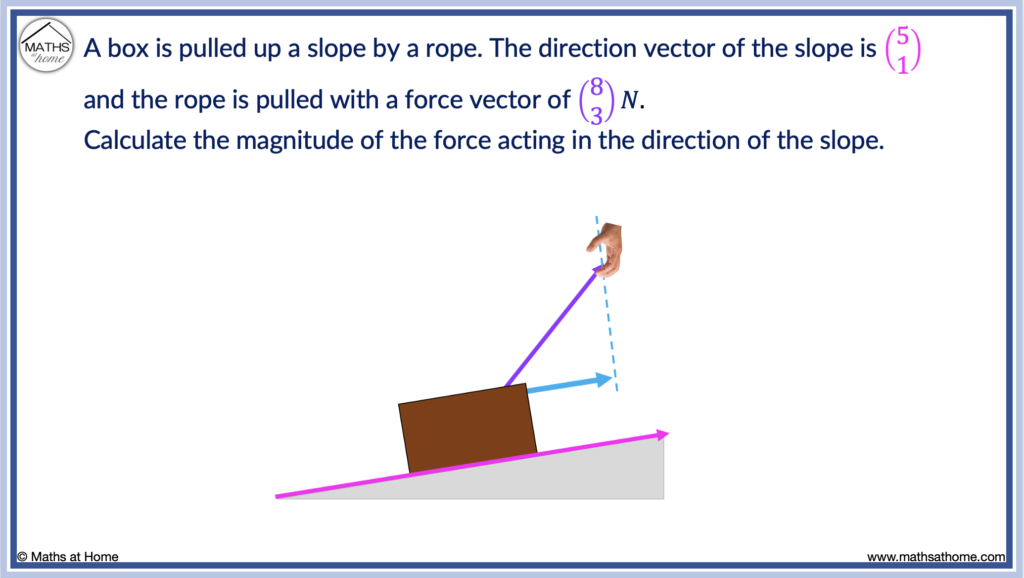
real life example of scalar projection

Since we want the magnitude of the force, the scalar projection is required.

In this example, the force is projected in the direction of the slope.

We choose the vector a right arrow to be the vector that is being projected and the vector b right arrow to be the vector that it is projected on to.

Therefore a right arrow equals the 2 by 1 column matrix 8 3 and b right arrow equals the 2 by 1 column matrix 5 1.

real life example of vector projection

The equation of the scalar projection, s equals the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of b right arrow becomes s equals the fraction with numerator open paren the 2 by 1 column matrix 8 3 times the 2 by 1 column matrix 5 1 close paren and denominator the absolute value of the 2 by 1 column matrix 5 1.

The dot product, the 2 by 1 column matrix 8 3 times the 2 by 1 column matrix 5 1 equals open paren 8 times 5 close paren plus open paren 3 times 1 close paren equals 43.

The magnitude of vector b right arrow, the absolute value of b right arrow equals the square root of 5 squared plus 1 squared equals the square root of 26.

Therefore the scalar product, s equals the fraction with numerator open paren the 2 by 1 column matrix 8 3 times the 2 by 1 column matrix 5 1 close paren and denominator the absolute value of the 2 by 1 column matrix 5 1 becomes s almost equals 8.43 N.

Therefore 8.43 N of force from the rope acts in the direction of the slope.

Vector Projection Calculator

This vector projection calculator calculates the projection of the vector A onto the vector B.

To use the calculator, simply input the 𝑥, y and z components of both vectors.

In this calculator, Vector A is always the vector being projected onto Vector B so it is important to put the vectors in the correct order.

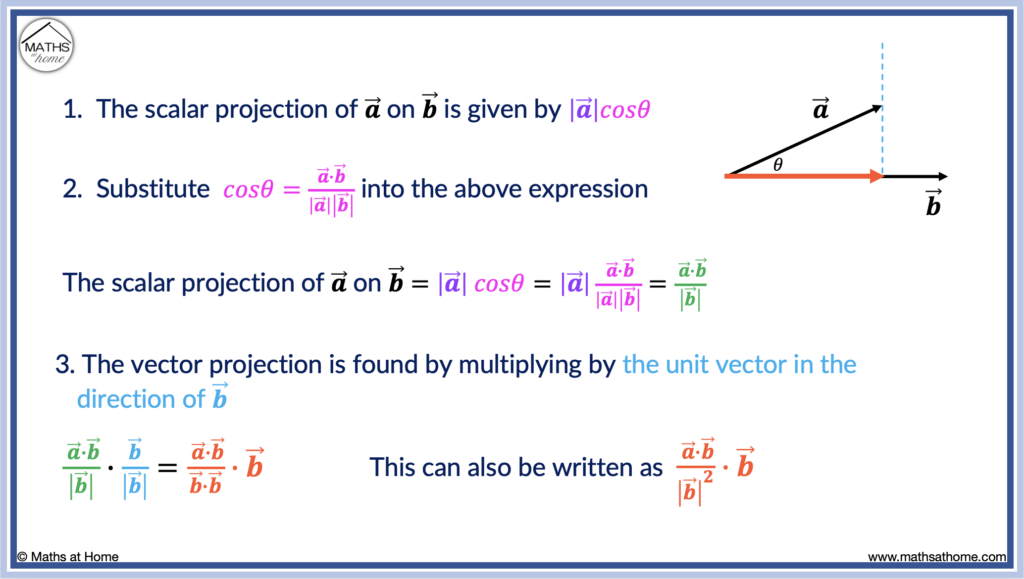
Vector Projection Proof

The scalar projection of ‘a’ on ‘b’ is given by a cosθ, where θ is the angle between the vectors. Substituting cosθ = (a⋅b) / ( |a||b| ) into this, we obtain a (a⋅b) / ( |a| |b| ). The vector projection is found by multiplying this by the unit vector in the direction of b to obtain (a⋅b) b / (b⋅b).

  1. The scalar projection of a right arrow on b right arrow is given by the absolute value of a right arrow times cosine theta
  2. Substitute cosine theta equals the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of a right arrow times the absolute value of b right arrow into this expression to obtain the scalar projection as the absolute value of a right arrow times the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of a right arrow times the absolute value of b right arrow. This simplifies to the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of b right arrow.
  3. The vector projection is found by multiplying this scalar projection by the unit vector in the direction of the vector b right arrow: the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of b right arrow times the fraction with numerator b right arrow and denominator the absolute value of b right arrow which simplifies to the fraction with numerator open paren a right arrow times b right arrow close paren and denominator the absolute value of b right arrow times the absolute value of b right arrow times b right arrow.
proof of the vector projection formula