Video Lesson: Finding an Angle in a Right-Angled Triangle
Finding Angles Using Trigonometry
Trigonometry relates angles and lengths in geometric shapes.
Right-angled trigonometry involves the relationship between the lengths of the three sides of a right-angled triangle (the opposite, adjacent and hypotenuse) and its angles.
In this lesson, we learn how to calculate missing angles in a triangle from two known sides.
It is very important to label the sides of a right-angled triangle correctly.
θ is the greek symbol theta. It is commonly used in mathematics to represent the unknown angle that we wish to calculate.
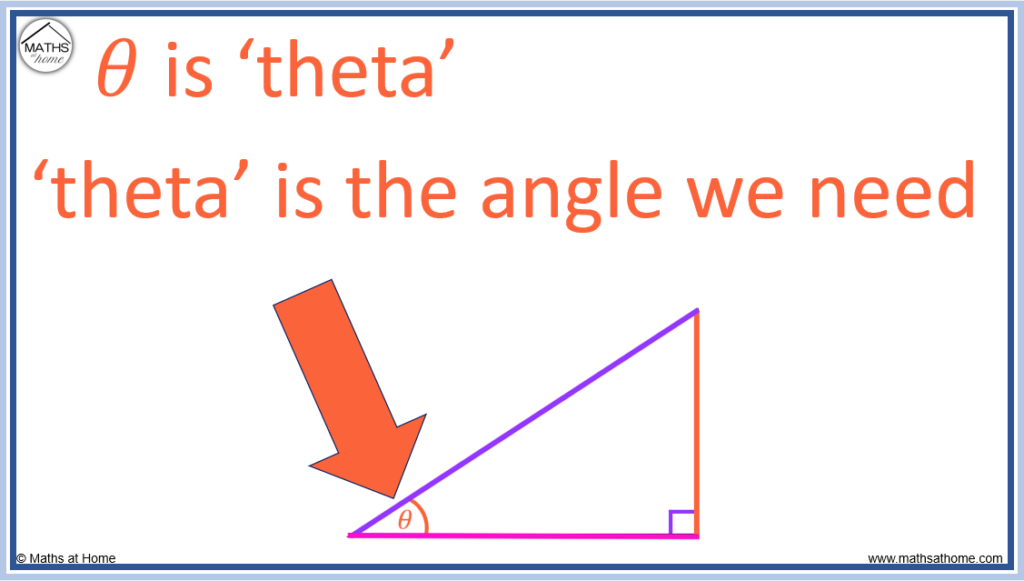
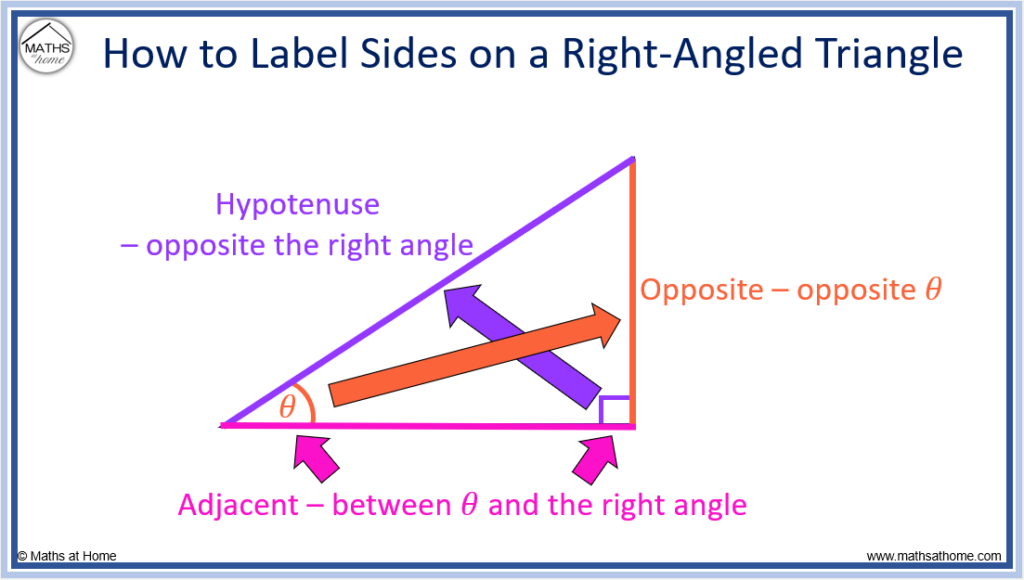
We use the following system to label sides on a right angled triangle:
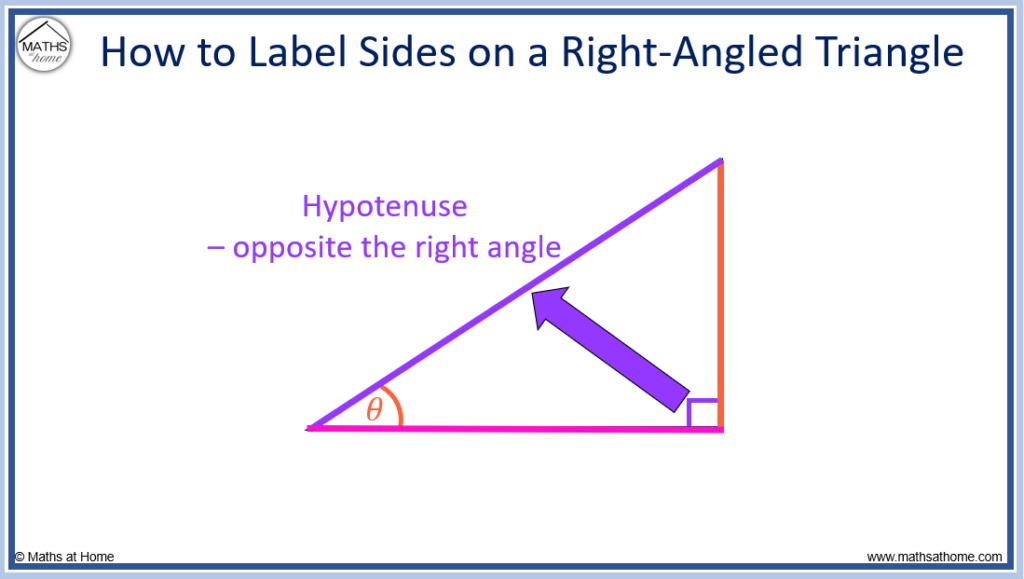
- The hypotenuse is the longest side and it is always opposite the right-angle.
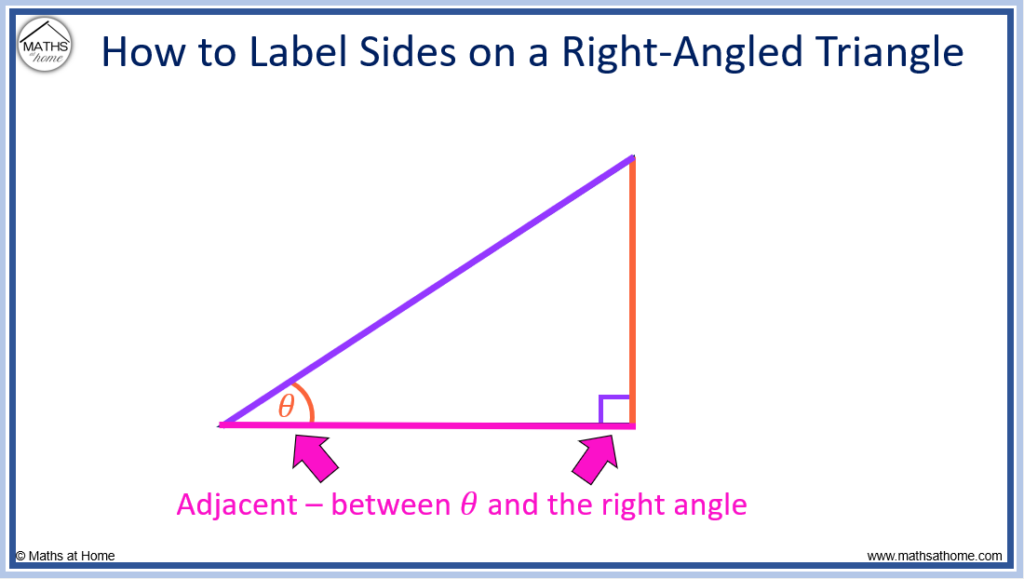
- The adjacent is the side in-between the angle θ and the right-angle.
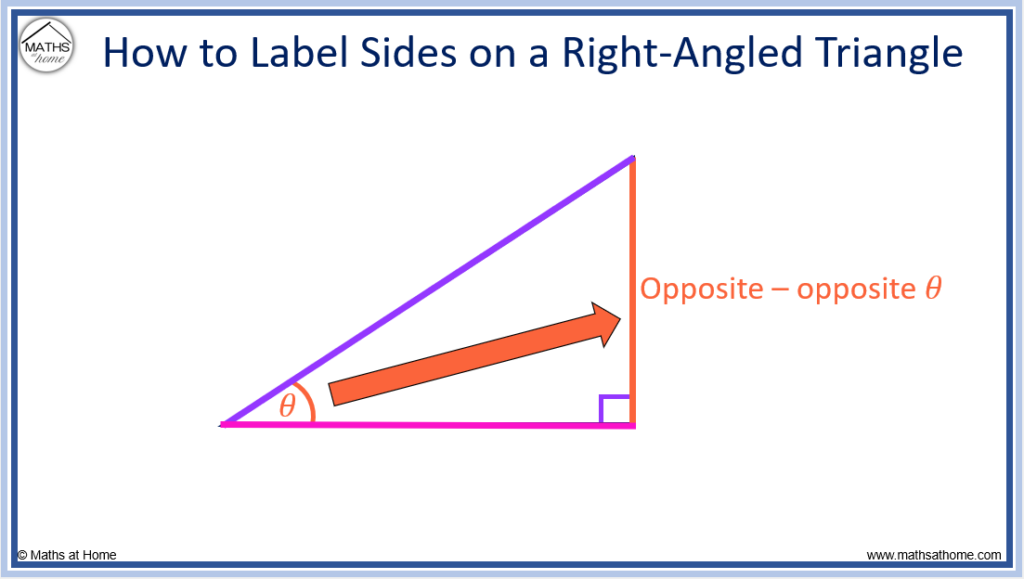
- The opposite is the side that is directly opposite the angle θ.
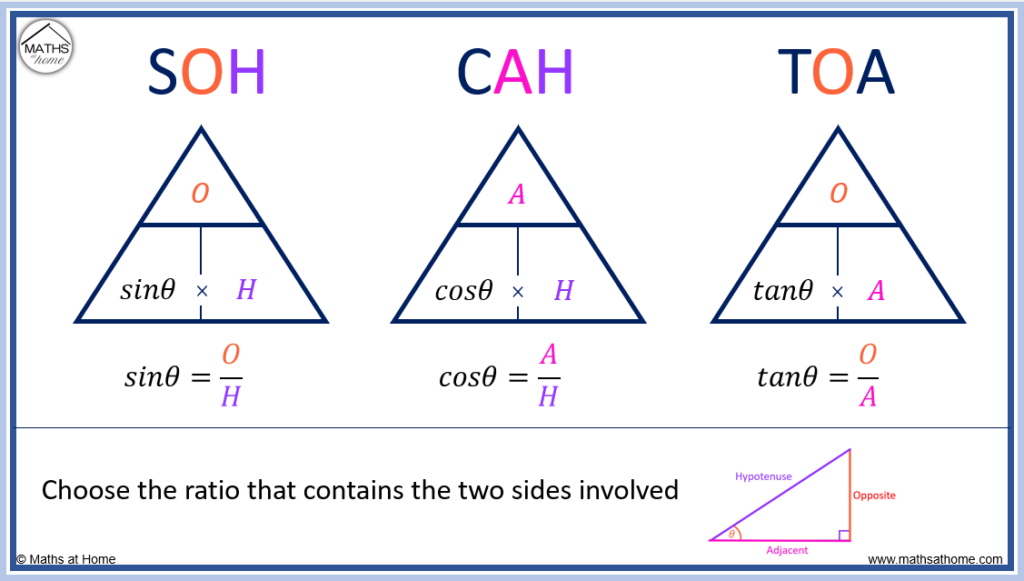
The relationship between the length of the three sides of a right-angled triangle and its angles is given by the three trigonometric ratios:
SOHCAHTOA is used to remember the three trigonometric ratios of sinθ=(O/H), cosθ=(A/H) and tanθ=(O/A).
In ‘SOH’: the ‘S’ stands for sinθ, the O stands for the opposite side and H stands for the hypotenuse.
In ‘CAH’: the ‘C stands for cosθ, the A stands for adjacent and H stands for the hypotenuse.
In ‘TOA’: the ‘T’ stands for tanθ, the O stands for the opposite and A stands for the adjacent.
The inverse of sine, cosine and tangent is used to rearrange the trigonometric ratio equations for the angle θ.
The inverse of sine is written as sin-1().
The inverse of cosine is written as cos-1().
The inverse of tangent is written as tan-1().
The trigonometric equations:
are rearranged for the angle theta and written simply as:
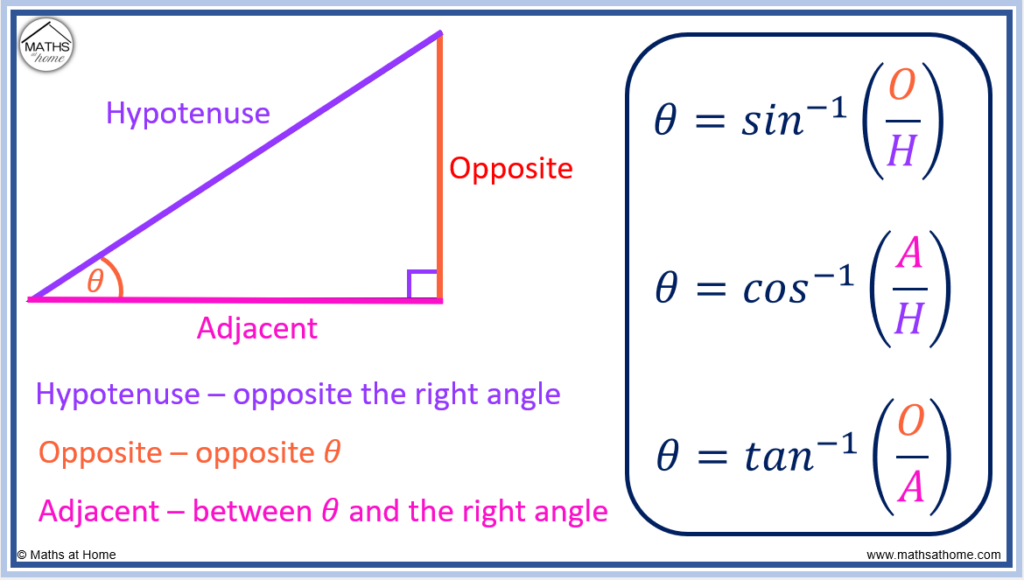
These three equations are used to calculate the missing angle in a right-angled triangle directly.
Again, the mnemonic of SOH CAH TOA can be used to remember the equations.
The first letter in each of SOH, CAH and TOA tells us whether it is sin, cos or tan.
The middle letter in each of SOH, CAH and TOA tells us which letter is the numerator of the fraction.
The final letter in each of SOH, CAH and TOA tells us which letter is the denominator of the fraction.
How to Find a Missing Angle in a Right-Angled Triangle Using Trigonometry
To find a missing angle using trigonometry:
- Label the two known sides as opposite, hypotenuse or adjacent.
- If O and H are known, θ = sin-1(O/H).
- If A and H are known, θ = cos-1(A/H).
- If O and A are known, θ = tan-1(O/A).
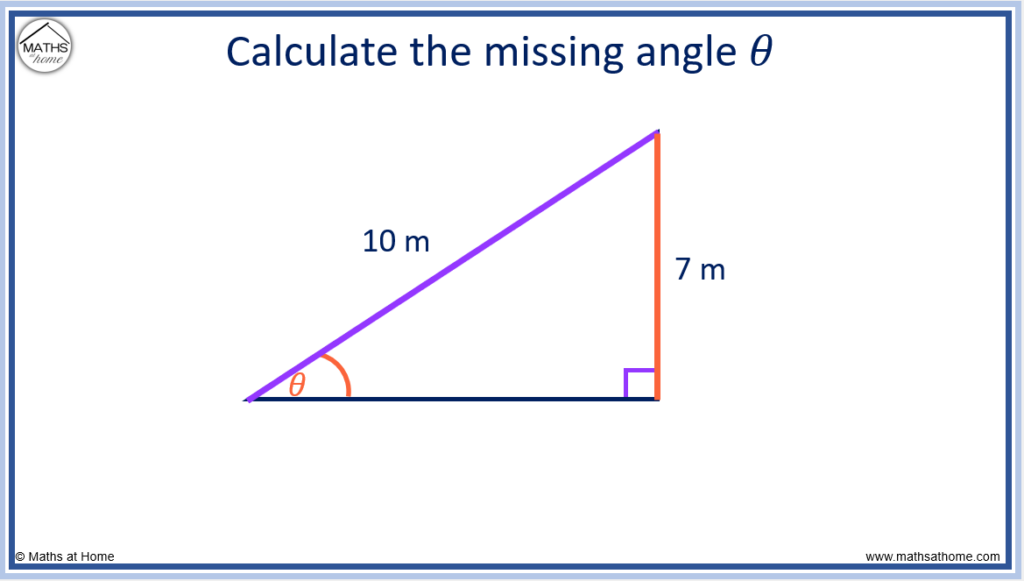
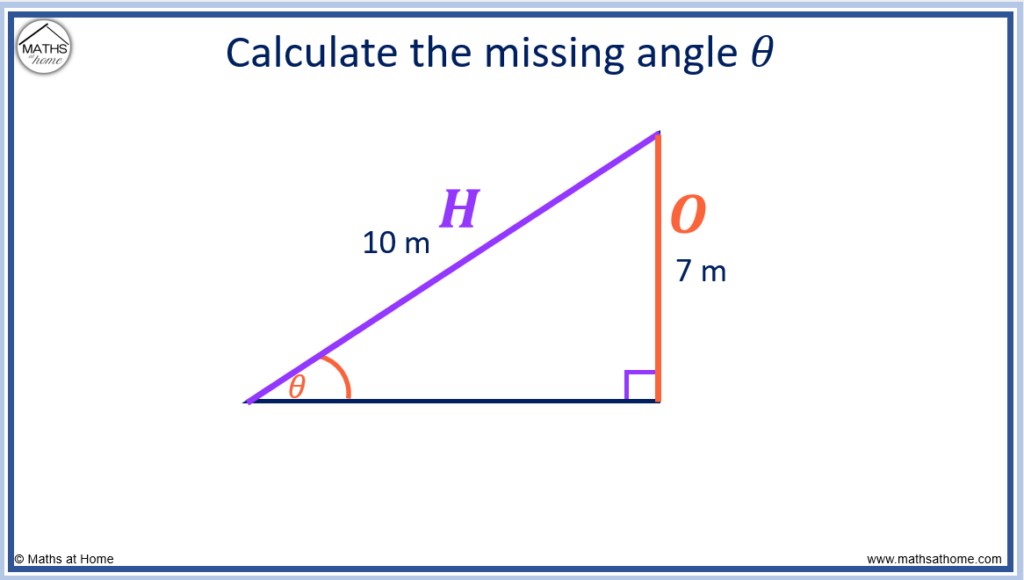
For example, calculate the missing angle θ in the right-angled triangle below.
Step 1. Label the two known sides as opposite, hypotenuse or adjacent
The first step in finding a missing angle on a right-angled triangle is to label the sides of the triangle.
The side opposite the right angle
The side between θ and the right angle
The side opposite θ
In our example, the 7m side is opposite θ and so it is the opposite side.
The 10m side is opposite the right-angle and so, it is the hypotenuse.
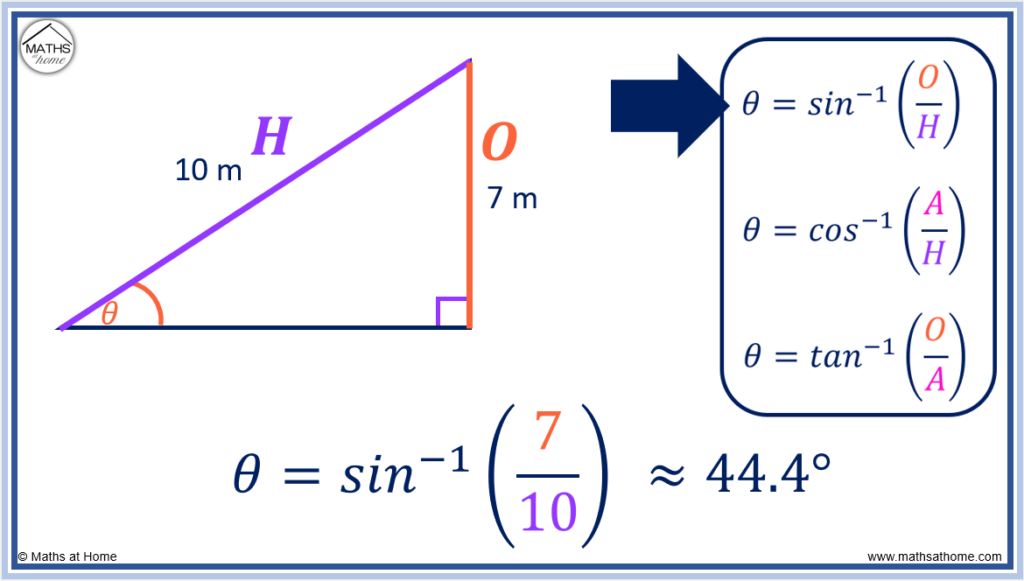
Step 2. Choose the correct formula involving the two known sides
The two known sides are the opposite (O) and the hypotenuse (H).
The equations for calculating a missing angle using trigonometry are:

In this example, we have both the O and the H sides.
The only equation involving both O and H is .
O = 7 and H = 10.
Therefore becomes
.
This can be entered into the calculator directly by typing which equals 44.4°.
sin-1, cos-1 and tan-1 are inverse sine, inverse cosine and inverse tangent respectively. They are always used to find missing angles using trigonometry.
To type sin-1, cos-1 and tan-1 on the calculator, press ‘shift’ or ‘2nd’ in the top left of the calculator and then press ‘sin’, ‘cos’ or ‘tan’ respectively.

To calculate a missing angle using sin, cos and tan, the triangle used must contain a right-angle.
The three equations
- θ = sin-1(O/H)
- θ = cos-1(A/H)
- θ = tan-1(O/A)
are used in right-angled triangles to find an angle from two known sides.
At least two sides of a triangle must be known in order to calculate a missing angle.
We will now look at some examples of calculating missing angles using trigonometry with solutions.
How to Find an Angle Using Sine (sin)
If the opposite (O) and hypotenuse (H) sides of a triangle are known, then the missing angle is found using the formula:
θ = sin-1(O/H).
The formula for finding a missing angle using sine
For example, calculate the missing angle on the right-angled triangle shown.
The opposite side is 5 cm long and the hypotenuse is 9 cm long.
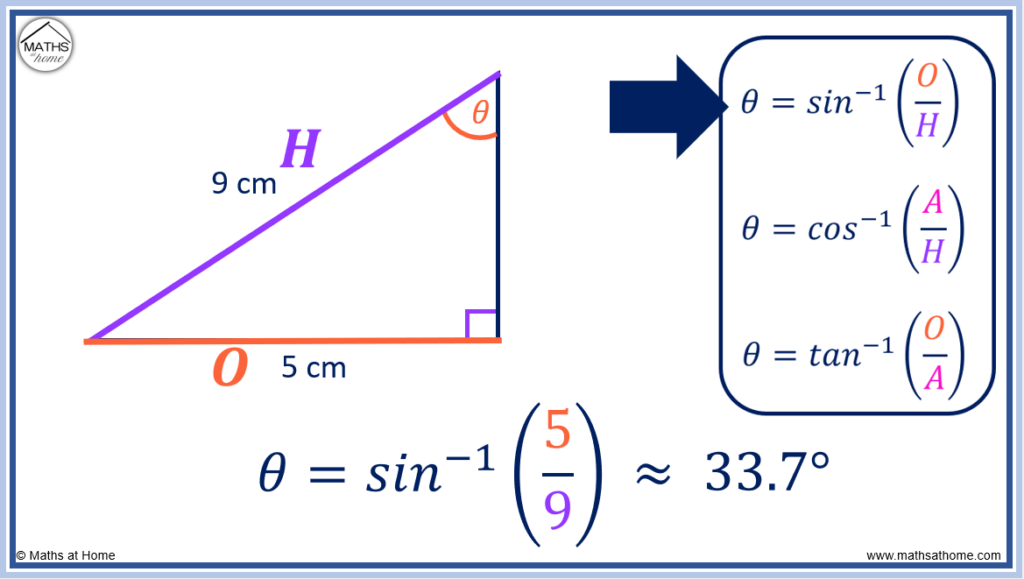
We substitute the values of O = 5 and H = 9 into the equation to obtain
.
We evaluate this using a calculator to obtain .
How to Find an Angle Using Cosine (cos)
If the adjacent (A) and hypotenuse (H) sides of a triangle are known, then the missing angle is found using the formula:
θ = cos-1(A/H).
The formula for finding a missing angle using cosine
For example, calculate the missing angle in the right-angled triangle shown.
The adjacent side (A) is 12 m and the hypotenuse (H) is 20 m.
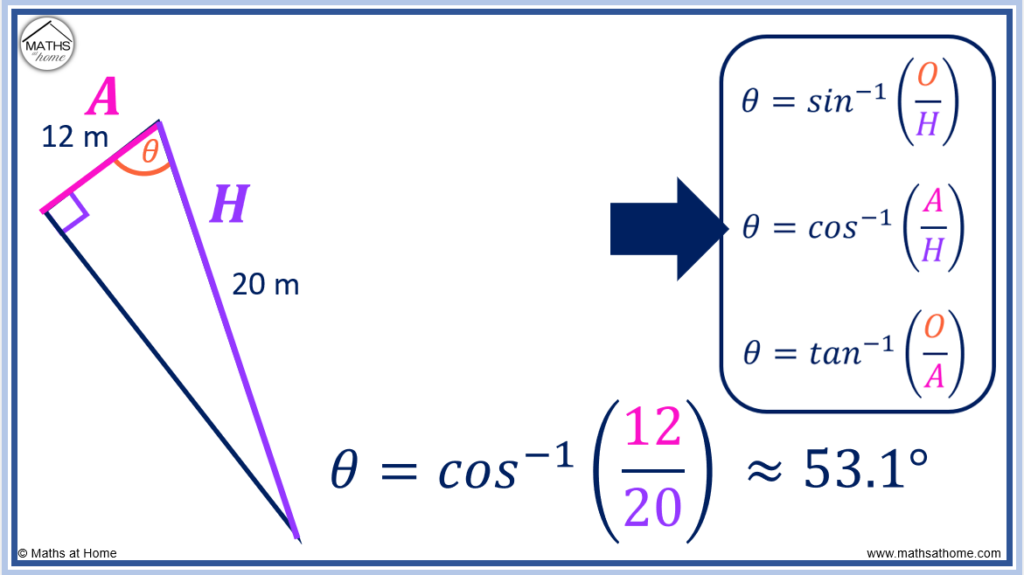
We substitute A = 12 and H = 20 into the equation to obtain
.
We evaluate .
How to Find an Angle Using Tangent (tan)
If the opposite (O) and adjacent (A) sides of a triangle are known, then the missing angle is found using the formula:
θ = tan-1(O/A).
The formula for finding a missing angle using tangent
For example, find the missing angle in the right-angled triangle shown.
The opposite side (O) = 3 m and the adjacent side (A) = 4 m.
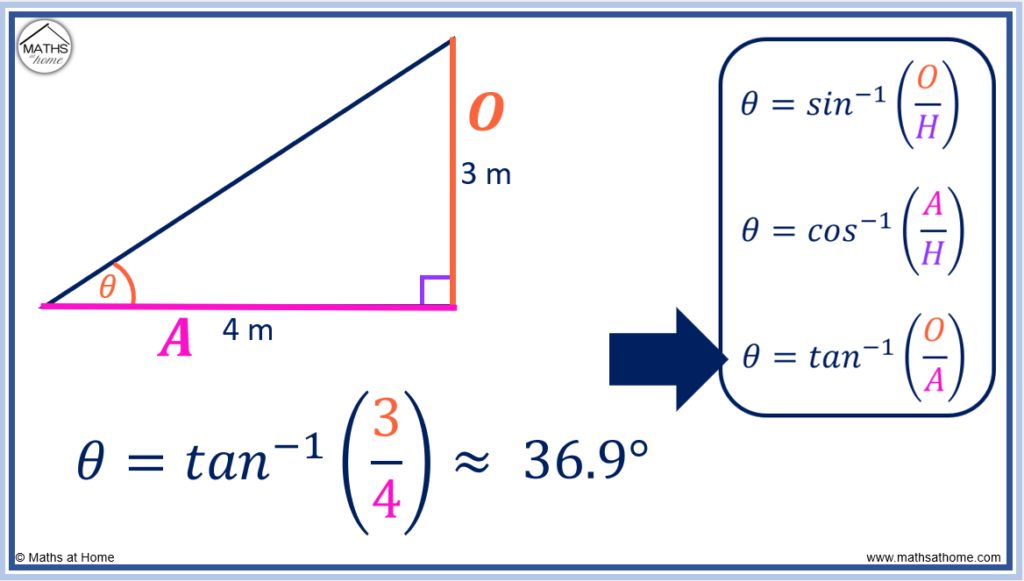
We substitute O = 3 and A = 4 into the equation to obtain
.
We evaluate this so that .
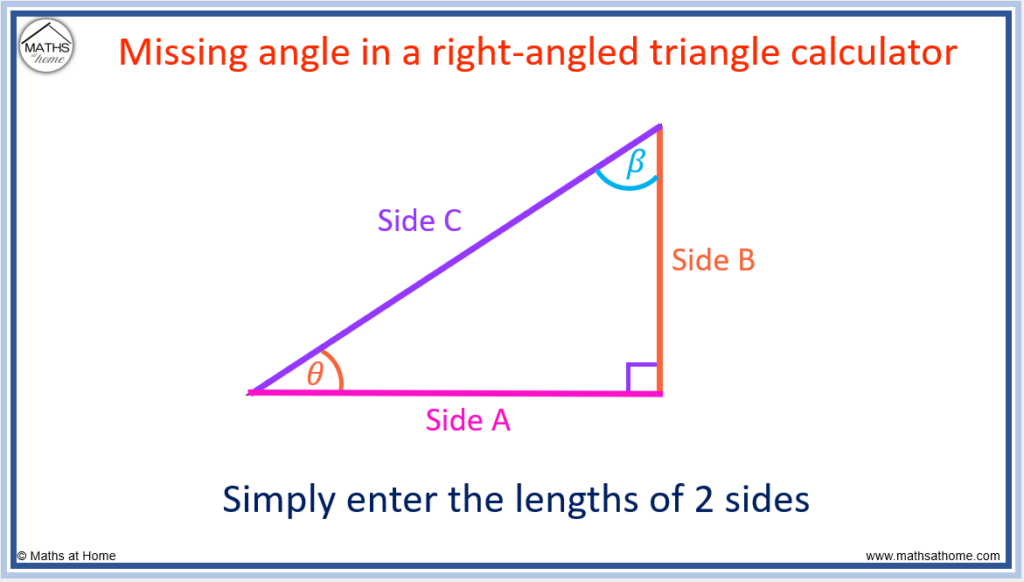
Calculator to Find Missing Angles Using Trigonometry
This online trigonometry calculator is used to find missing angles in a right-angled triangle.
Simply enter two of the side lengths as listed in the diagram shown.
Examples of Calculating Angles Using Trigonometry
Here are some examples of using trigonometry to calculate angles in real life problems.
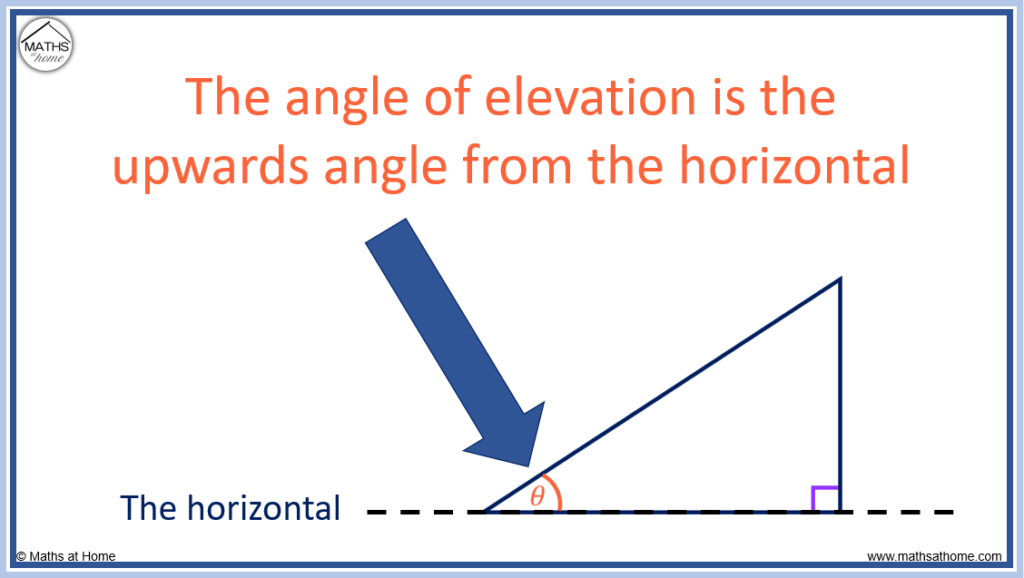
The angle of elevation is the angle from the horizontal line up to a point.
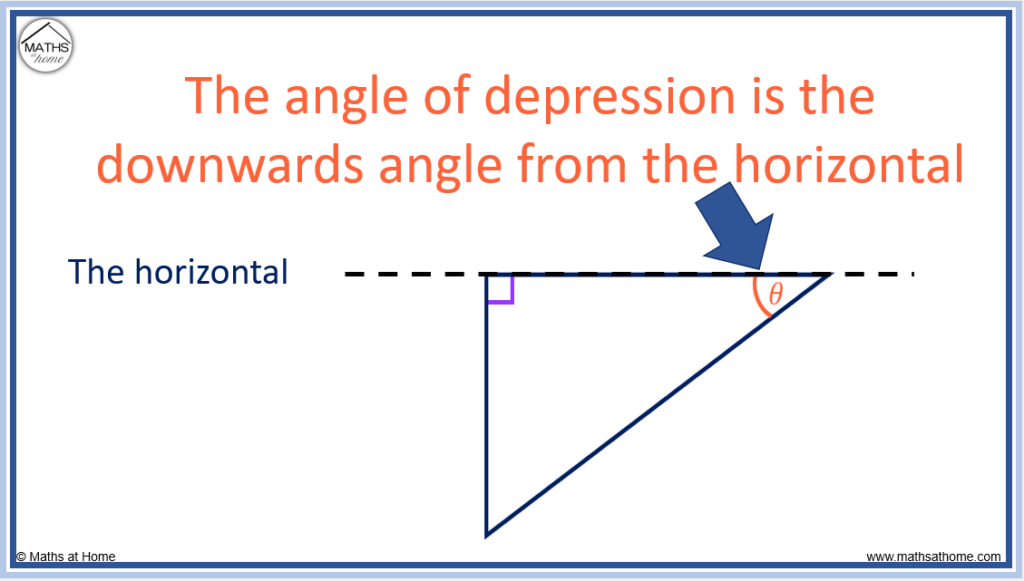
The angle of depression is the angle from the horizontal line down to a point.
Both the angle of elevation and the angle of depression are always measured from a horizontal line.
For example, a man is 20m away from a lighthouse that is 55m tall. What is the angle of elevation from the man to the top of the lighthouse?
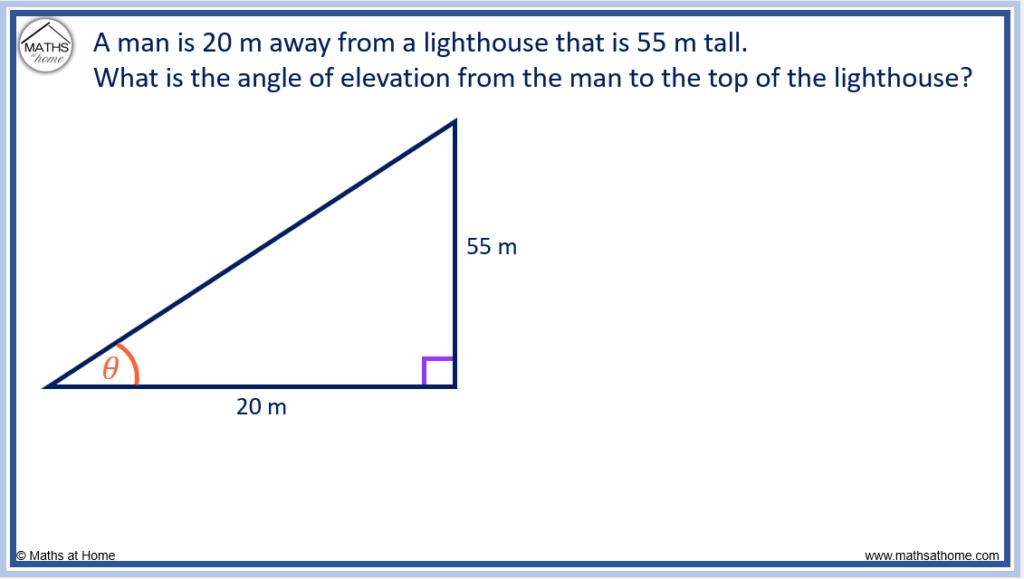
The angle of elevation is marked with θ. It is the angle from the horizontal upwards to the top of the lighthouse.
The distance that the man is from the lighthouse is 20m and this is marked as the adjacent side (along the ground from the man to the lighthouse).
The height of the lighthouse is 55m and so, this is the vertical side of the triangle and it is the opposite side.
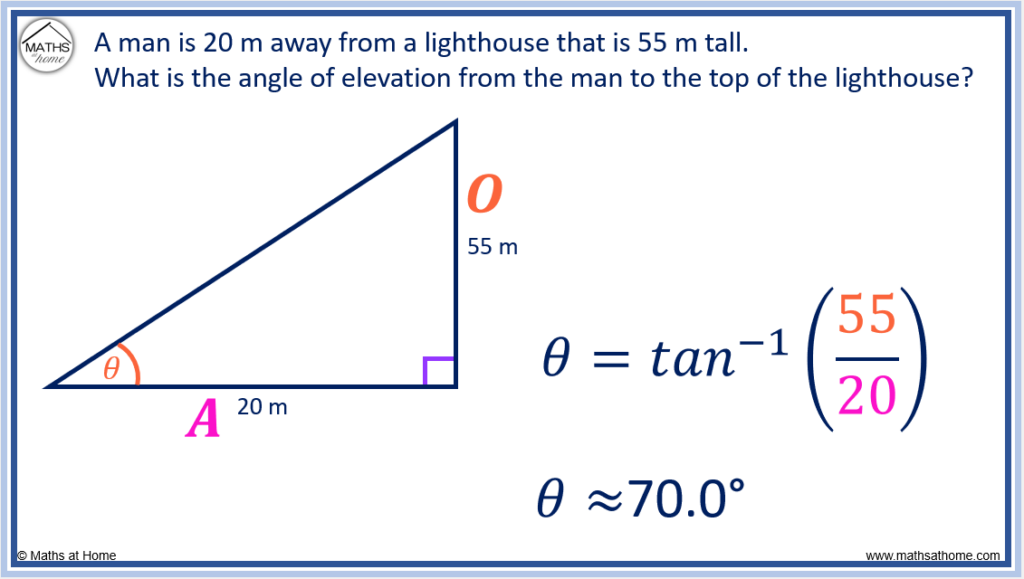
Since we know the adjacent and opposite side, we use the formula .
Substituting O = 55 and A = 20, this becomes .
Evaluating this, we obtain .
For example, a kite is flying 30m above the ground and it is attached to the ground by a string of length 60 m.
Calculate the angle of depression from the kite to the ground.
The angle of depression is shown marked by θ on the diagram below.
It is the angle downwards from the horizontal.
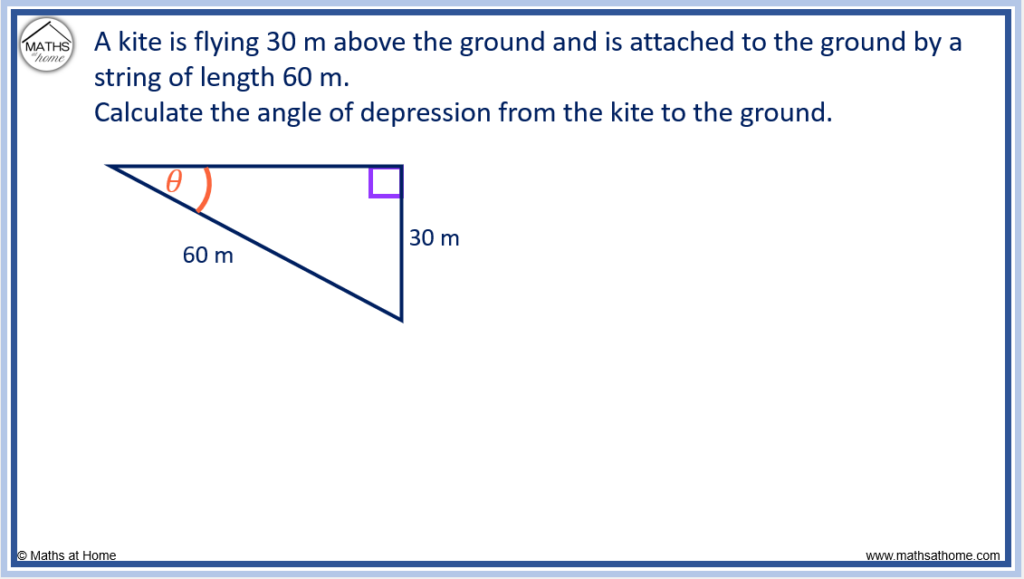
The string is connected from the kite to the ground. This is not a vertical string and it forms the hypotenuse of the triangle shown with length 60m.
The kite is 30m above the ground and this is a vertical length, so it forms the opposite side.
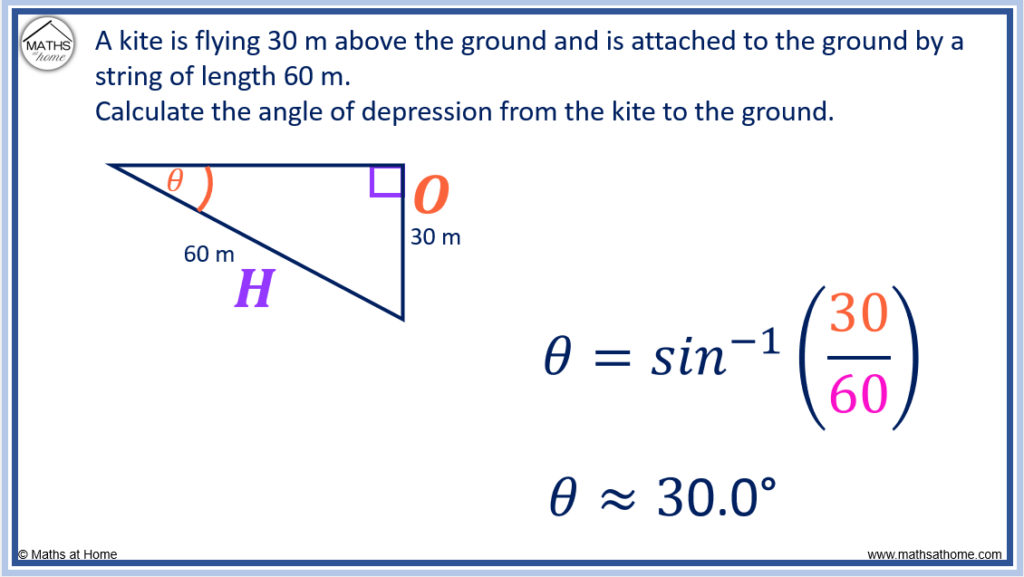
Since we know the opposite side and the hypotenuse, we use the formula .
We substitute O = 30 and H = 60 into the equation to obtain .
Evaluating this, we obtain
