A Complete Guide: Proof by Mathematical Induction with Products

Video Lesson: Proof by Induction with Products

Pi Product Operator Notation

The symbol ∏ is the pi product operator (or product series). Its meaning is to substitute all integer values from the starting value to the final value into the expression that follows and then multiply together all of the outputs.

The pi product notation

For example, in the case of :

• The initial value is 1
• The final value is 5
• Substitute all integer values between 1 and 5 as ‘i’ into the following expression
• The following expression is just ‘i‘ so we just substitute the numbers 1 to 5
• Then we multiply the outputs together

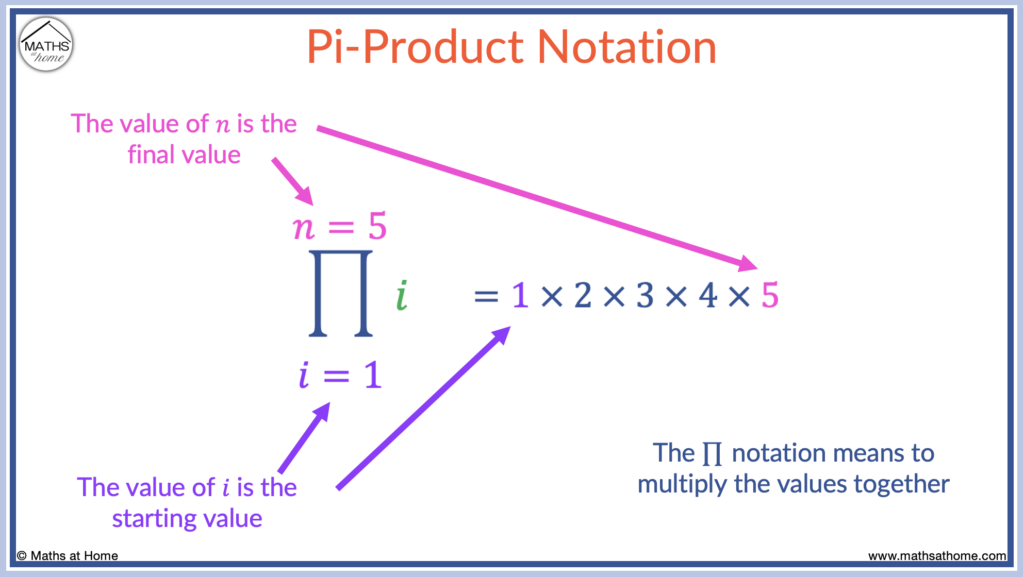
Therefore,

---

Here is another example:

• The initial value is 1
• The final value is 4
• Substitute all integer values between 1 and 4 as ‘i’ into the following expression
• The following expression is ‘(3i-1)‘
• Then multiply the outputs together

• When ‘i’ = 1, the output of ‘(3i-1)’ is 2
• When ‘i’ = 2, the output of ‘(3i-1)’ is 5
• When ‘i’ = 3, the output of ‘(3i-1)’ is 8
• When ‘i’ = 4, the output of ‘(3i-1)’ is 11

We multiply all of these outputs together to obtain .

Steps for Mathematical Induction with Products

The steps for mathematical induction with products are:

1. Show the statement is true for the base case (often n = 1).
2. Assume the statement is true for the case of n = k.
3. Use this assumption to prove that the statement is true for n = k + 1.
4. Conclude the proof.

How to do Mathematical Induction with Products

In simple terms, to do mathematical induction for products:

1. Substitute a simple value (such as n = 0 or n = 1) into the statement and show it is true.
2. Substitute n = k into both sides of the statement and assume the result is true.
3. Substitute n = k + 1 into both sides of the statement. We will then try to prove this.
4. Substitute the result from step 2 into the expression on the left hand side.
5. Simplify this expression further to show that it is equal to the expression on the right hand side.
6. State that since the statement is true for the base case and it is true for n = k + 1 provided that it is true for n = k, then it must be true for all given values.

For example, prove that for .

It is first important to understand what this question is asking.

The pi product symbol means to substitute values from 1 to n into the following expression of and then multiply them together.

is read as ‘where n is an element of the positive integer set’. This means that we will only consider the positive whole numbers from 1 to n. It is just used to clarify which values this statement is true for. For example, we won’t substitute decimal or negative values into this expression.

means that we will substitute , , etc. all the way up to a final value of Then we write it as these results all multiplied together.

Doing this, we obtain ….

We can write this more simply as .

Therefore we wish to prove that .

Step 1. Show that the statement is true for a base case

In this step, we simply substitute a simple value of n into the statement to show that it is true.

We must choose a value of n that is within the set of numbers being considered. We have , which means that n must be any positive integer.

We will use n = 1 as this is the simplest case. We substitute n = 1 into both sides of the statement. On the left hand side of the equation, we substitute and go no further.

Therefore,

becomes which simplifies to which is true.

This step shows that the proof is true for the case where n = 1.

If we wished, we could have chosen another simple value of n as the base case. For example, if n = 2,

becomes .

This simplifies to , which is also true.

We only need to verify one base case and it makes sense to do this for the smallest possible value of n in our given domain.

Step 2. Assume that the statement is true for n = k.

We write out in full as .

We now substitute n = k into this equation to obtain .

We will assume that this equation is true.

This result will be used in the following step.

Step 3. Use the assumption of step 2 to show that the statement is true for n = k + 1

We have already assumed that the statement is true for n = k.

That is: .

We will now write the statement which we wish to show to be true. That is, that it is true for n = k + 1.

The original equation is .

Substituting n = k + 1 into this, we obtain:

This simplifies to:

.

This is what we will try to prove.

We can see that contains the result from step 2, which is: .

We can substitute this result from step 2 into this equation to obtain:

.

Now we need to show this is true algebraically.

Expand the brackets to obtain:

Now we multiply the first term by so that the two fractions have a common denominator. We obtain:

Now we can write the two fractions as one fraction like so:

, which simplifies to:

.

Now we can cancel the terms on the top and bottom of the fraction to obtain:

.

Since the left hand side of the equation is now equal to the right hand side, we have completed this step.

Step 4. Conclude the proof

To conclude proof by induction, we simply make a statement containing the following information:

• The statement was true for the base case.
• The statement is true for the n=k+1 case provided that the n=k case was true.
• The statement is true for all required values of n.

Our conclusion to the proof is the following:

Since the statement is true for the base case where n = 1 and it is true for n = k + 1 whenever n = k is true, the rule is true for all required values of n.

The case of n=k+1 refers to the next integer after the n=k case.

We have assumed that the n=k case is true and used this fact to prove that the n=k+1 case is true.

This means that as long as one case is proven true, we know that the following case is also true.

Therefore, the case after that will be true and so on.

Since we have verified the base case (when n=1), we know that the statement is true for n=2, n=3 and so on.

Proof by induction is often compared to domino chains. The logic is that we know that when one domino falls, it will knock over the next domino. Then we know that the first domino is knocked over then we know that all of the following dominos will fall over.

Here we know our first case is true and therefore, all following cases will be true as well.

Proof by Induction with Products: Examples and Solutions

Here are some examples of questions involving proof by induction with products.

For example: Prove that .

This means: prove that

Notice that we start with the initial value of n = 2 in this question.

Step 1. Show that the statement is true for a base case

Here we are given that , which means that our values of n must be integers (whole numbers).

We are also given that , which means that the smallest value of n is 2.

We will use n = 2 to verify the base case.

When n = 2, the statement of becomes .

Therefore, we evaluate both sides to obtain which is true.

Step 2. Assume the statement is true for n=k

We take the full statement of and substitute n = k to obtain:

.

As part of the proof by induction process, we will assume this to be true and we will substitute this equation into our algebra in the next step.

Step 3. Use the assumption from step 2 to prove that the statement is true for n = k + 1

We substitute n = k+1 into to obtain the statement that we wish to prove, which is:

We can simplify this to:

.

Now we substitute the assumption from step 2: in to obtain:

.

Now we need to rearrange the expression on the left of the equals sign to show that it is equal to the expression on the right of the equals sign.

We start by expanding the brackets to obtain:

We can simplify this to obtain:

Now we multiply the first term by so that the denominators are:

We can expand the bracket on the first term to obtain:

We can write this as one fraction as:

and this simplifies to:

We can factor k out of the numerator to obtain:

and dividing the numerator and denominator by k, we prove the required result:

.

Step 4. Conclude the proof

Since the statement is true for the base case where n = 2 and it is true for n = k + 1 whenever n = k is true, the rule is true for all required values of n≥2.

---

Here is another example.

Prove that is odd for n≥2.

This means that the product of is odd.

Step 1. Show that the base case is true

In this question, n ≥ 2 and so, we must consider values of n greater than 2.

We will use n = 2 as the base case.

Substituting n = 2, the expression is .

Since we do not have a given rule that it is equal to, this example is a little different. We can show that this result is odd by simply calculating it.

which is an odd result.

Therefore the base case has been shown to be true.

Step 2. Assume the statement is true for the case where n = k

Before we proceed with the usual process, we will consider what it means for the result to always be odd.

An odd number is always formed when any given integer is doubled and then one is subtracted.

Therefore an odd number can be represented by 2A-1, where A is any integer.

For the case where n = k, we can write:

, where .

Step 3. Use the assumption in step 2 to prove the statement true for n = k + 1

We take the given expression: and substitute n=k+1 to obtain:

.

We can expand the final term to obtain:

This simplifies to: .

Now we can substitute the assumption from step 2, which was:

.

The equation becomes: .

Our job is to expand this and show that the result is also odd.

Expanding, we obtain: .

We can factor the 2 out of the first three terms to obtain: .

Now, whenever we subtract 1 from a multiple of 2, we have an odd result.

is just an integer, since A and k are integers too. Therefore is odd.

Step 4. Conclude the proof

Since the statement is true for n = 2 and it is true for the case of n = k + 1 whenever n = k is true, the statement is true for all n ≥ 2.

---

Here is another example.

Prove that for that

, where .

Step 1. Verify the statement is true for a base case

We will consider the case where n = 1.

When n = 1, the equation becomes:

This simplifies to: which simplifies to .

We can write this as:

Cancelling the in the fraction, we obtain: .

Therefore the base case has been proven true for n = 1.

Step 2. Assume the statement is true for the case where n = k

We substitute n = k into the equation:

to obtain:

.

Step 3. Use the assumption in step 2 to prove the statement is true for the case where n = k + 1

We consider the original statement:

When n = k + 1, the statement becomes:

This can be simplified as:

Which can be written as:

We can substitute the assumption from step 2:

into the left hand side of the equals sign to obtain:

This can be written as:

Now the numerator of can be expanded so that:

And therefore, the equation can be written as:

And since:

We can write:

.

Therefore the statement is true for n = k + 1 whenever it is true for n = k.

Step 4. Conclude the proof.

Since the statement is true for the base case of n = 1 and it is true for the case of n = k + 1 whenever it is true for n = k, the statement is true for all n.