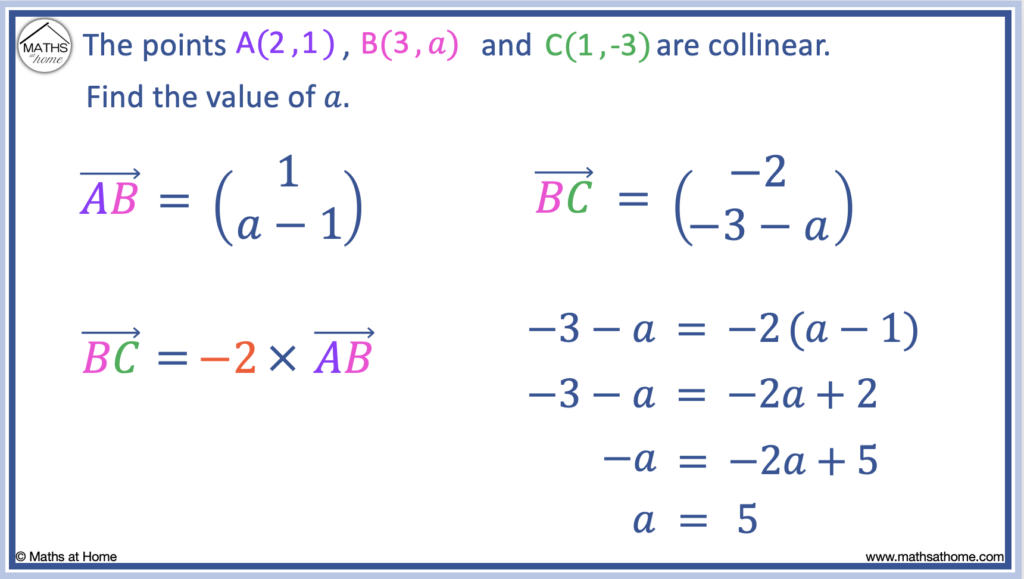How to Show that Points are Collinear

Video Lesson: Collinear Vectors

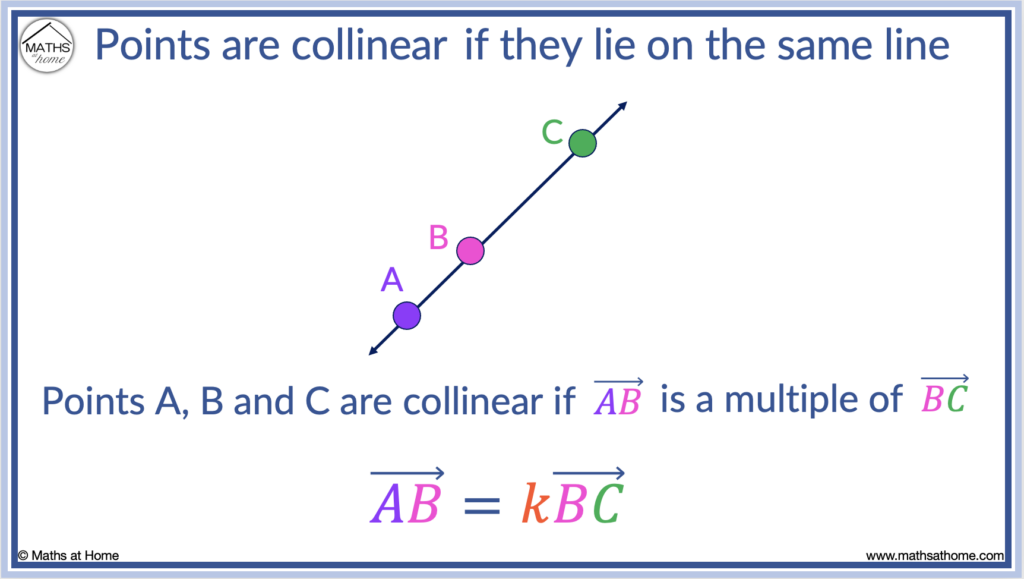
What are Collinear Points?

Collinear points are points that lie on the same line. Points A, B and C are collinear if the vector AB is a multiple of vector BC. That is because if two vectors are parallel and share a common point, they are on the same line.

The points A, B and C shown below lie on the same line and therefore the points are collinear.

definition of collinear points

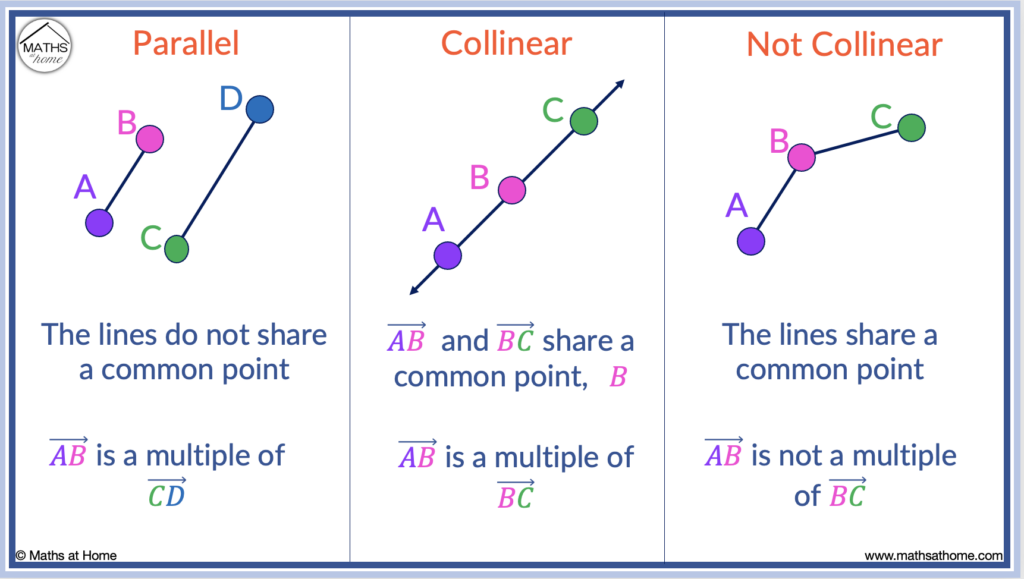
Parallel vectors are vectors that are oriented in the same direction.

If vectors are parallel, one vector is a multiple of the other vector.

For example, A B right arrow equals the 2 by 1 column matrix Row 1: 3 Row 2: negative 2 and C D right arrow equals the 2 by 1 column matrix Row 1: 6 Row 2: negative 4 are parallel vectors since C D right arrow equals 2 times A B right arrow.

It is important to note that parallel vectors are not always collinear.

For example, in the image below, A B right arrow is parallel to C D right arrow but they do not share a common point. They are parallel but they are not on the same line.

If two vectors are parallel and share a common point, the points are on the same line and are therefore collinear.

the difference between collinear and parallel vectors

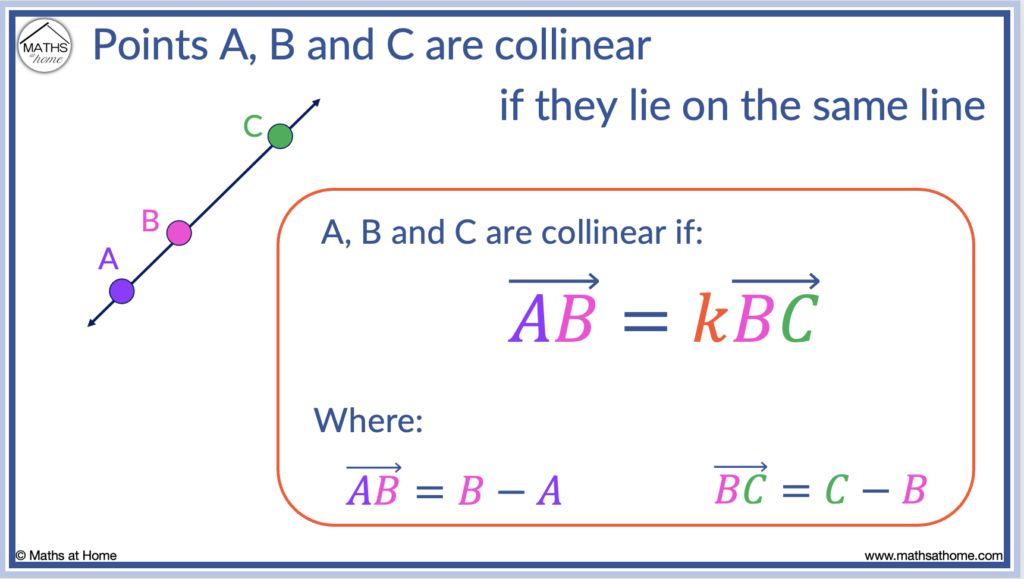
Points A, B and C are collinear if A B right arrow and B C right arrow are parallel.

That is because both A B right arrow and B C right arrow share a common point, B.

The vectors A B right arrow and B C right arrow do not need to be the same magnitude to be collinear. Only their direction matters.

If the vectors A B right arrow and B C right arrow are not parallel then the points are not collinear. This is shown in the rightmost image above.

Points in space are collinear if they lie on the same line. However, most applications of vectors involve free vectors, which do not have a position. Therefore the meaning of collinearity is different for vectors.

Vectors are collinear if they are parallel to the same line. Therefore collinear vectors are parallel to each other. That is, one vector is a multiple of the other.

How to Show Points are Collinear Using Vectors

To show that points A, B and C are collinear:

  1. Find the vectors AB and BC.
  2. If vector AB is a multiple of BC, the points are collinear.
  3. If vector AB is not a multiple of BC, the points are not collinear.
how to show points are collinear using vectors

For example: Decide if the points A(2, 3), B(6, 7) and C(8, 9) are collinear.

Step 1. Find the vectors AB and BC

The vector A B right arrow is found by subtracting A from B.

A B right arrow equals B minus A

A B right arrow equals the 2 by 1 column matrix Row 1: 6 minus 2 Row 2: 7 minus 3 equals the 2 by 1 column matrix 4 4

The vector B C right arrow is found by subtracting B from C.

B C right arrow equals the 2 by 1 column matrix Row 1: 8 minus 6 Row 2: 9 minus 7 equals the 2 by 1 column matrix 2 2

Step 2. If vector AB is a multiple of BC, the points are collinear

A B right arrow equals the 2 by 1 column matrix 4 4 and B C right arrow equals the 2 by 1 column matrix 2 2

The values in vector A B right arrow are twice as large as those in vector B C right arrow .

Therefore, A B right arrow equals 2 times B C right arrow.

A B right arrow is a multiple of B C right arrow and so, the points are collinear.

how to show that 3 points are collinear using vectors

Here is an example of points that are not collinear.

Decide if the points A(1, 4), B(2, 5) and C(6,3) are collinear.

Step 1. Find the vectors AB and BC

A B right arrow equals B minus A and so, A B right arrow equals the 2 by 1 column matrix 1 1.

B C right arrow equals C minus B and so, B C right arrow equals the 2 by 1 column matrix 4 negative 2.

Step 2. If vector AB is a multiple of BC, the points are collinear

Now, the vector A B right arrow is not a multiple of B C right arrow since the 𝑥 component of 1 was multiplied by 4 to obtain 4 but the y component of 1 was multiplied by -2 to make -2.

Therefore, the points are not collinear.

example of points that are not collinear

Formula for Determining Collinearity

The formula used to determine if points are collinear is AB = k BC. That is, if the vector AB is a multiple of the vector BC, the points A, B and C are collinear.

A B right arrow equals k B C right arrow

The formula for determining if vectors A B right arrow and B C right arrow are collinear.
formula for showing points are collinear

Points A, B and C are collinear if the vectors A B right arrow and B C right arrow are parallel.

Vectors are parallel if one vector is a multiple of the other.

That is written as A B right arrow equals k B C right arrow.

How to Show Points are Collinear Using Distance

An alternative method for determining if points are collinear is to use the magnitude of the vectors between them.

The magnitude of a vector is its length.

For a given vector a right arrow equals the 2 by 1 column matrix a sub 1 a sub 2, its magnitude is given by the absolute value of a right arrow equals the square root of a sub 1 raised to the 2 power plus a sub 2 raised to the 2 power.

Points A, B and C are collinear if the magnitude of the vector AB plus the magnitude of vector BC is equal to the magnitude of vector AC. The formula for determining if points are collinear is |AB| + |BC| = |AC|.

the absolute value of A B right arrow plus the absolute value of B C right arrow equals the absolute value of A C right arrow

The formula to show points are collinear using magnitudes of vectors
formula for collinear points

If the distance from A to B plus the distance from B to C is equal to the distance from A to C, the points must be in a line.

If the points are not in a line, the distance from A to B plus the distance from B to C will always be greater than the distance from A to C.

For example, show that the points A(4, -3), B(7, 1) and C(10, 5) are collinear using the distance formula.

how to show that points are collinear using distance

The points A, B and C are collinear if the absolute value of A B right arrow plus the absolute value of B C right arrow equals the absolute value of A C right arrow.

To show the points are collinear, we will show that this statement is true.

A B right arrow equals the 2 by 1 column matrix 3 4 and therefore the absolute value of A B right arrow equals the square root of 3 squared plus 4 squared equals 5.

the absolute value of B C right arrow equals the square root of 3 squared plus open paren negative 4 close paren squared equals 5.

the absolute value of A C right arrow equals the square root of 6 squared plus 8 squared equals 10.

Therefore since 5 + 5 = 10, the absolute value of A B right arrow plus the absolute value of B C right arrow equals the absolute value of A C right arrow and so, the points are collinear.

How to Prove that Vectors are Collinear

Two vectors between points are collinear if their cross product is equal to zero. For example, the vector AB = [5, 5] and the vector BC = [-3, -3]. Their cross product is equal to zero and they are collinear.

Considering the points A(-1, 1), B(4, 6) and C(1, 3), show that they are collinear.

We first find the vectors A B right arrow equals the 2 by 1 column matrix 5 5 and B C right arrow equals the 2 by 1 column matrix negative 3 negative 3.

We then find their cross product using the formula A B right arrow times B C right arrow equals x sub 1 y sub 2 minus x sub 2 y sub 1.

A B right arrow times B C right arrow equals open paren 5 times negative 3 close paren minus open paren 5 times negative 3 close paren equals 0.

If the cross product of two vectors is equal to zero, the points they pass through are collinear.

Therefore, these points are collinear.

how to show vectors are collinear using the cross product

How to Show that Points are Collinear in 3D

The 3 dimensional points A, B and C are collinear if the vector AB is a multiple of the vector BC. For example if the vector AB is [2, -3, -1] and the vector BC is [-6, 9, 3], the points are collinear because the vector BC is equal to the vector AB multiplied by -3.

The vector A B right arrow is found by subtracting the point A from the point B.

A B right arrow equals the 3 by 1 column matrix 7 negative 5 2 minus the 3 by 1 column matrix 5 negative 2 3 equals the 3 by 1 column matrix 2 negative 3 negative 1

The vector B C right arrow is found by subtracting the point B from the point C.

B C right arrow equals the 3 by 1 column matrix 1 4 5 minus the 3 by 1 column matrix 7 negative 5 2 equals the 3 by 1 column matrix negative 6 9 3

Now B C right arrow equals negative 3 times A B right arrow.

Therefore the points are collinear.

Find the Value for Which the Points are Collinear

To find a missing coordinate given that the points A, B and C are collinear:

  1. Find vectors AB and BC in terms of the missing value.
  2. Write vector AB as a multiple of the vector BC.
  3. Solve the resulting equation for the unknown coordinate.

For example, the points A(2, 1), B(3, a) and C(1, -3) are collinear. Find the value of ‘a’.

We first find the vector A B right arrow by subtracting vector A from vector B.

A B right arrow equals the 2 by 1 column matrix 3 a minus the 2 by 1 column matrix 2 1 equals the 2 by 1 column matrix Row 1: 1 Row 2: a minus 1

Then we find vector B C right arrow by subtracting vector B from vector C.

B C right arrow equals the 2 by 1 column matrix 1 negative 3 minus the 2 by 1 column matrix 3 a equals the 2 by 1 column matrix Row 1: negative 2 Row 2: negative 3 minus a.

By comparing the first component of A B right arrow with the first component of B C right arrow, we can see that B C right arrow equals negative 2 times A B right arrow.

Therefore, we can write the equation for the second component.

negative 3 minus a equals negative 2 times open paren a minus 1 close paren

We now solve this for a.

negative 3 minus a equals negative 2 a plus 2

a equals 5.